Leonardo Ceragioli & Valentina Luporini

Intuition is not (always) immediate, and this is good news!

Attached document(s)

Annexes

• Texte complet en PDF/Full text in PDF: Vol. XIX, n°3, p. 180-204 (722k)

Résumé

In this paper, we aim to propose a taxonomy of the notion of intuition. In particular, we will develop a distinction that is only sketched in the contemporary debate: that between phenomenological and epistemic intuitions. After that, we will argue that both kinds of intuitions further split into immediate and non-immediate. Once the taxonomy is built, we will investigate the relations between these different kinds of intuitions. Finally, we will focus on non-immediate phenomenological intuitions wondering whether they have a justificatory role.

Table of content

Introduction

1This paper speaks about intuition. Intuition is classically meant to be a faculty of a priori non-inferential rational insight, delivering propositional knowledge – knowledge of truths. Such truths are also generally taken to be modally loaded, i. e. necessarily true.¹

2Yet, intuition is not a notion that persuades everyone. For the skeptic, intuition remains mysterious, supernatural, and self-congratulatory.²

3In this paper, we will take for granted the dignity of intuition and focus on another story.³ In particular, we aim to point out and further develop a distinction that is only sketched in contemporary epistemology: that between the so-called phenomenological and epistemic intuitions. Paradigmatic cases of the former can be found in (Chudnoff, 2020) and (Bengson, 2015); cases of the latter in (Hales, 2000), (BonJour, 1997), and (Strawson & Bealer, 1992).

4When considering intuition, it is important to distinguish between intuition as a faculty and its products, namely intuitive sentences. In this paper, we will use the term “intuition” as referring to both of them. Yet, the distinction between epistemic and phenomenological intuitions just concerns intuitive sentences.

5Phenomenological intuitions are those sentences that seem true. Classic example: Pythagoras’ theorem. Phenomenological intuitions share some main features. They are presentational in the sense that they directly and immediately present the world as being in a certain way;⁴ they also are forceful or pushy, and provoke the feeling of rightness.⁵

6Epistemic intuitions are a subset of phenomenological intuitions. They have all the phenomenological features and peculiarly regard the basic principles of our theories. In this sense, they provide a well-grounded foundation for our knowledge. An example is the transitivity of identity, claiming that if a = b and b = c, then a = c.

7It is clear now why the distinction between epistemic and phenomenological intuitions does not apply to intuition as a faculty. The faculty is always phenomenological in that it has phenomenological features. By contrast, the distinction acquires importance for intuitive sentences.

8Moreover, we will stress that both phenomenological and epistemic intuitions further split into immediate and non-immediate. More specifically, we will argue that the criterion for distinguishing between immediate and non-immediate epistemic intuitions is based on the relation between the understanding of the meaning of some sentences and the decision of their truth values. For phenomenological intuitions, the distinction between immediate and non-immediate relies on an extensional comparison with epistemic intuitions.

9Generally speaking, we will explore the distinction between immediate/non-immediate phenomenological intuitions and immediate/non-immediate epistemic ones. We will then point out their main relations. This will allow us to build a more accurate taxonomy of the notion of intuition to reframe the contemporary debate in a more fine-grained way.

10After displaying the taxonomy, we will focus on non-immediate phenomenological intuitions, and further distinguish between those that concern theorems and those that concern their proofs. More specifically, we will consider (Koksvik 2013)’s and (Chudnoff 2019)’s positions according to which the intuition of the validity of the proof is constitutive of that of the truth of the theorem. We will argue that we have good reasons to endorse this position but also that we have cases in which it fails. Then, we will discuss whether intuition still has epistemic appeal even when its content consists of theorems that have a proof. We will consider Koksvik’s reply according to which intuition increases the degree of justification. We will argue nonetheless that this thesis is problematic.

11The paper has 5 sections. Section 1 explores the main distinction between epistemic and phenomenological intuitions, and points out that these are not mutually exclusive labels. In Section 2, we will introduce a further distinction: that between immediate and non-immediate intuition. We will argue that this distinction can be meaningfully applied to epistemic intuitions. In Section 3, we will extend the distinction to phenomenological intuitions. In Section 4, we will focus on non-immediate phenomenological intuitions and evaluate whether they have justificatory power. Section 5 concludes.

1. Phenomenological and epistemic intuitions

12As mentioned, phenomenological intuitions are those sentences that seem true, while epistemic intuitions are those that regard the basic principles of our theories.

13Even though epistemic intuitions are a subset of phenomenological ones, there is a difference between them. Phenomenological intuitions allow for degrees. For instance, arguably, Pythagoras’ theorem is less intuitive than Triangle Inequality⁶. Given their status of starting points, epistemic intuitions do not admit degrees. For instance, there is no axiomatic system in which we accept the transitivity of identity in some degrees. Either we accept it, or we do not. Despite this difference, it is clear from how we have defined epistemic and phenomenological intuitions that they are not mutually exclusive. For instance, in (Hales, 2000), the author seems to first refer to epistemic intuitions, while in, (Hales, 2012), he focuses on their phenomenological features.

14It is not a case that Hales first speaks about epistemic intuitions. Indeed, the first way to defend intuition from the skeptic is to prove its epistemic appeal. Such proof is, so to say, indirect or purely existential in that it does not say what intuition is. The dialectic goes rather as follows: intuition may be mysterious but is of course indispensable to grant certain important principles which cannot arguably be granted otherwise (see (Strawson & Bealer, 1992)). In this sense, epistemic intuitions are necessary starting points that we assume to be justified for building knowledge. Once granted the epistemic dignity of intuition, phenomenological features of intuition display how intuition is supposed to work. Then, we do a phenomenology of intuition which is a way to directly reply to the question of what it is.

15In what follows, we will explore a further distinction that regards both epistemic and phenomenological intuitions: that between immediate and non-immediate intuitions.

2. Non-immediate and immediate epistemic intuitions

16Often intuitions are taken to be immediate. What it is for an intuition to be immediate? And, more specifically, what it is for an epistemic intuition to be immediate? We argue that an epistemic intuition is immediate when the following principle fails to apply:

17Two steps (2S): The decision of a sentence S consists of two different steps: i) the understanding of S, and ii) the decision of its truth value.

18An example of a sentence for which 2S holds is given by (Wright, 2004): “I have left my keys in the garage”. Indeed, it is possible to understand its meaning without being able to decide its truth value (if, for example, we have not yet come back in the garage when we consider the proposition).⁷

19An example of a sentence that does not fit 2S, and is then immediate in our sense is “Modus Ponens is valid”. Modus Ponens (MP) is a schema for a deductive argument and a rule of inference. It can be summarized as “P implies Q. P is true. Therefore Q must also be true”. Now, it is plausible to claim that if someone understands MP, they already know that it is true. In other words, the rule for MP is “constitutive” of the understanding of the conditional, and vice-versa⁸.

2.1 Immediate epistemic intuitions

20As anticipated, MP plausibly is a case of immediate epistemic intuitions. Other examples are the following sentences:

21 

22A. If an object is completely red, then it cannot be completely green;

23B. No colour without extension;

24C. A sound has an amplitude;

25D. Each occurrence of lightness is associated with an occurrence of saturation.

26 

27A and B are classic examples of Husserl’s material a priori propositions (see (Husserl, 1900/1), chapter 11). C and D correspond to (Benardete, 1958)’s cases of analytic a posteriori sentences.⁹

28The reason why these sentences do not fit 2S is clear: We cannot understand them without already knowing that they are true.

2.2 Non-immediate epistemic intuitions

29Can epistemic intuitions be non-immediate? We argue that they can. More specifically, we claim that the only way in which we can spot epistemic non-immediate intuitions is to focus on errors and disagreements. The reason is clear. Indeed, if we have errors or disagreements concerning some sentences, then the decision of their truth values cannot be constitutive of their meaning.¹⁰

30To understand how errors and disagreements apply to intuitive sentences, let us distinguish between systematic and accidental failures.

31Systematic failures are errors that a given faculty cannot avoid making. They are, so to say, part of its standard working procedure – even though they lead to erroneous beliefs. These failures are independent of both the behavior of the epistemic subject and the environment in which they occur. Hence, they cannot be rectified.

32A classic example of systematic failure is that of a thing that appears smaller than it really is the farther we are from it. Other more recent examples are the horizontal lines of Muller-Lyer’s arrows that appear to be of different lengths, the stick half immersed in water which appears to be bent at the surface, and Adelson’s checker shadow illusion in which a given area of the checker appears to be a darker color than another. For an example of systematic error of hearing, consider a sound that contains all of an overtone series except the fundamental but that is erroneously perceived as if it contained it.¹¹

33Accidental failures are errors that can be rectified. They occur either when a given faculty does not work as intended, or because of certain environmental causes.

34Examples of the first kind of accidental failures are blindness and amnesia – respectively related to vision and memory. For an example of the second kind, consider again Wright’s proposition. Regardless of any vision problem, a given subject would not be able to decide the proposition if, for instance, they are not in the garage or the light is turned off. Given this taxonomy, we can say that a good example of epistemic intuitive sentences that fit 2S are sentences that are systematically wrongly decided by intuition.

35An example is the well-known comprehension principle (CP), which asserts that, given a condition expressed by a formula φ(x), there is a set that contains all and only those objects o such that φ(o). Trivial as it could seem, CP leads to the famous paradox discovered by Russell, and so it cannot be true. Nonetheless, it is hard to deny its intuitive appeal: it still seems true after we discover that it cannot be.

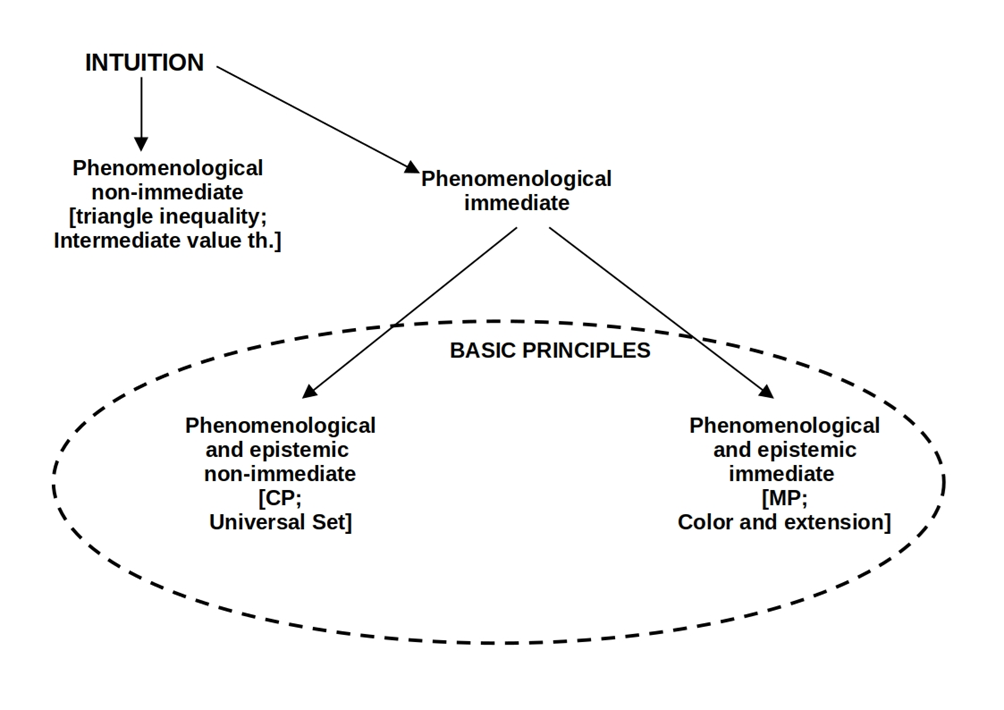
36Another case is the intuition that there should be a universal set that contains every object. Mathematicians would be glad to postulate or derive its existence. Unfortunately, the universal set is prima facie incoherent with Cantor’s theorem. Despite this, the existence of the universal set maintains its intuitive appeal.

37Another case is the intuition which suggests that there are fewer odds numbers than natural ones. After Cantor’s theory of transfinite numbers, we know that this intuition is at least partially false. A case more related to philosophy stricto sensu is Gettier’s problem for the intuition that knowledge is justified true belief.¹²

38Finally, it could be asked whether there are cases of true epistemic intuitions which fit 2S and which are then non-immediate. To exemplify non-immediate epistemic intuitions, we have taken the case of errors because it is the way in which 2S becomes evident. However, we can find other cases of non-immediate epistemic intuitions that are not errors prima facie. An example can be found by looking at the problem of disagreement in logic. Consider the case of two subjects, one who believes in the excluded middle, the other that rejects it. Given that logic is necessary, then one is wrong and the other is right. What is important is that both of them understand the statement relative to the excluded middle.

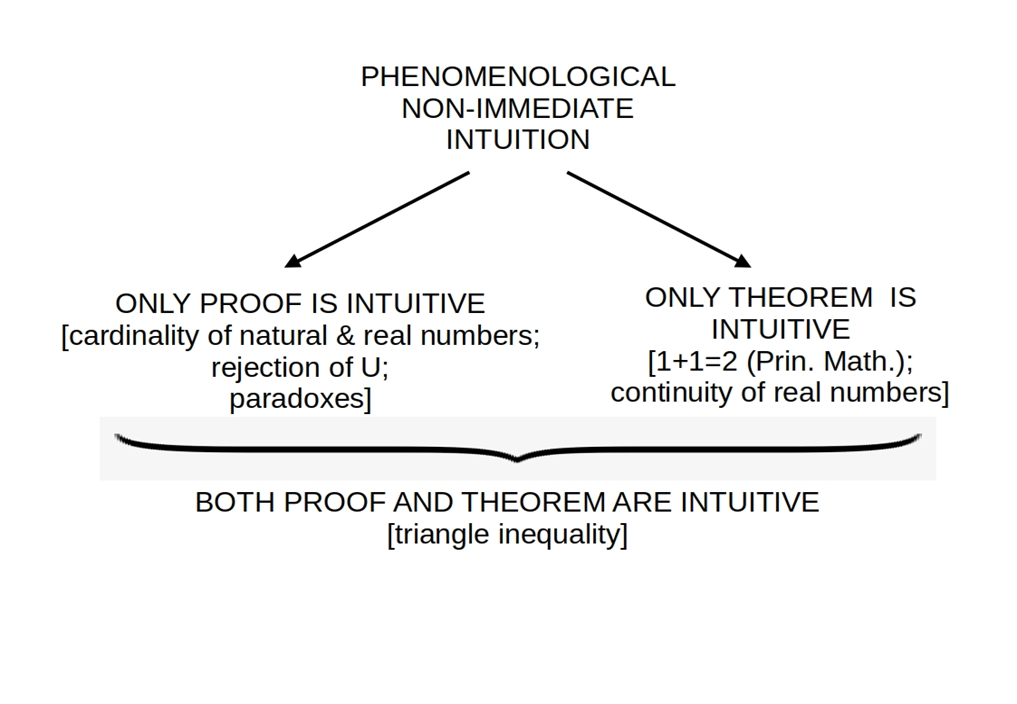
2.3 Further clarifications regarding epistemic intuitions

39Someone could object that the distinction between immediate and non-immediate epistemic intuitions is fuzzy. They can point out that the only way of spotting a non-immediate epistemic intuition is a failure of intuition or a disagreement between speakers. Nonetheless, before such a failure is observed or such a disagreement occurs, there is no reason not to consider such intuition as epistemically immediate.

40As a consequence, someone could suggest that all intuitions start as immediate and are considered non-immediate only after they are questioned. It could even be proposed that any intuition is non-immediate, if rightly analyzed. However, this does not seem to be the case. This slippery slope is not compelling just because certain sentences, such as A, B, C, and D, seem to be unquestionable. Moreover, the distinction is fuzzy only in an epistemic sense: an intuition is immediate or non-immediate; we just discover that it is (or not), given some particular situations and with some particular degrees of certainty.

41To summarize, all epistemic intuitions are non-inferential prima facie justified starting points and basic axioms of our epistemic enterprises. Epistemic intuitions can be immediate or non-immediate. The distinction between immediate and non-immediate epistemic intuitions is grounded on how their epistemic role is connected with understanding. More specifically, we have seen that 2S allows us to discriminate immediate from non-immediate intuitions by investigating the relation between the understanding and the decision of their truth values. If we cannot understand an intuitive sentence without already knowing its truth value, then it is immediate; if, otherwise, it is non-immediate. Examples of the first are “MP is valid” and “No color without extension”. Examples of the second are “The universal set exists” and “CP is valid”.

42Before moving on to phenomenological intuitions, another clarification is needed. Both immediate and non-immediate epistemic intuitions are justified using the faculty of intuition, or at least this is the position endorsed in this paper. The difference between immediate and non-immediate intuitions only regards the relation between intuition and linguistic competence. If linguistic competence is enough to decide a given supposedly intuitive sentence S, then S is immediate. We have therefore two cases: either we do not understand S, and so we cannot decide its truth-value, or we do understand S and we rightly decide its truth-value. But we do not have a case in which we understand S without rightly deciding its truth-value. On the other hand, if linguistic competence is not enough to decide a given supposedly intuitive sentence S, then S is non-immediate and there can be both errors and disagreements about its truth value.

43In both cases, it is important to notice that intuition has a role in the decision of sentences in question. Nonetheless, the situation could be a little puzzling. If a given sentence is decided by linguistic competence, which role can intuition have? The answer, according to our perspective, is the following: the fact that linguistic competence is enough to decide the sentence in question does not suggest that intuition is not used to gain linguistic competence. As an example, you can think that the sentence “brown is more similar to red than light blue” is analytically true and acquired using vision. In the same way, you can believe that the validity of MP is decided using intuition and that it is constitutive of the meaning of the conditional. By simplifying a little, we could say that intuition is immediate when it is needed to acquire linguistic competence, and non-immediate when it is applied to a sentence that can already be understood.¹³

44What happens with phenomenological intuitions?

3. Non-immediate and immediate phenomenological intuitions

45The distinction between immediate and non-immediate epistemic intuitions is easily pointed out by using 2S. By contrast, from the phenomenological point of view, things seem more complicated. Indeed, the application of 2S to phenomenological intuitions does not provide the distinction between immediate and non-immediate phenomenological intuitions. Trivially, all phenomenological non-epistemic intuitions suit 2S: since they are not starting points of our theories, they must be justified in other ways, and this justification requires a distinction between understanding and decision.

46We argue that the distinction between immediate and non-immediate phenomenological intuitions can be spelled out by referring to epistemic intuitions.

3.1 Immediate phenomenological intuitions

47We claim that phenomenological intuitions are immediate iff they are epistemic. Examples of immediate phenomenological intuitions are MP and CP. Indeed, they are basic principles respectively of logic and set theory. Moreover, they clearly display the phenomenological characters of intuitiveness.

3.2 Non-immediate phenomenological intuitions

48By contrast, phenomenological intuitions are non-immediate iff they are not epistemic. Examples of phenomenological non-immediate intuitions are Pythagoras’ theorem and the intermediate value theorem.¹⁴

49It can be asked what is the sense of distinguishing between immediate and non-immediate phenomenological intuitions by using epistemic intuitions. We argue that epistemic intuitions are good candidates for displaying the distinction because they allow us to discriminate between non-immediate intuitions that result from some processes of justification, and those that hold before such processes occur, which are therefore immediate.

50To sum up, some phenomenological intuitions are epistemic. Among the epistemic, we have intuition which are immediate (examples are: MP, red cannot be green, color has extension, sound has amplitude, lightness comes with saturation) and non-immediate (examples are: CP, universal set, fewer odds than natural numbers). The criterion for discriminating between immediate and non-immediate epistemic intuitions is 2S. Also, we have argued that phenomenological intuitions split into immediate and non-immediate. They are immediate when epistemic (example are: MP and CP) and non-immediate when non-epistemic (examples are: triangle inequality and intermediate value).

51Notice that a sentence can be phenomenologically immediate but epistemically non-immediate. CP is an example of this kind. This has not to be considered a problem. It just shows two senses in which the notion of immediacy can be spelled out. Of course, the other way round does not apply. We cannot have cases of phenomenologically non-immediate but epistemically mediate sentences just because, by definition, for a sentence to be phenomenologically immediate, it has to be epistemic.

52To sum up, the taxonomy of intuitions after all such considerations assumes the following form:

Another general clarification is in order. To present our taxonomy of intuitions, we have mainly focused on cases of axioms and theorems. Of course, we can also find examples of intuitions that cannot be considered either theorems or axioms. Some of these sentences are more close in nature to axioms and others to theorems. An example of the first kind is sentence D of section 2.1 “each occurrence of lightness is associated with an occurrence of saturation” which is not stricto sensu an axiom but serves as a starting point for an intuitive theory of colors. Examples of the second kind of sentences can be found considering infamous puzzles in analytic philosophy. Consider, for instance, the intuition that the ship of Theseus survives the replacement of one of its parts. This is not, strictly speaking, a theorem. It does not directly follow from any axiom. Yet, since it is classically considered to be the result of an argument, and has phenomenological intuitive appeal, it can be considered a case of non-immediate phenomenological intuition.¹⁵

53In this paper, we mainly focus on cases of theorems and axioms just because this makes it easier to distinguish between starting points and things that follow from such starting points and so, a fortiori, between epistemic and phenomenological intuitions.¹⁶

4. Non-immediate phenomenological intuitions: intuitiveness of theorems and intuitiveness of proofs

54In this section, we will focus on non-immediate phenomenological intuitions. In particular, we will wonder whether such intuitions have justificatory power.

4.1 Intuition of theorems and proofs: a prima facie taxonomy

55Phenomenological non-immediate intuitions can concern the content of the theorem, its proof, or both of them. Thus, we have 3 different cases: the first concerns cases in which both the content of the theorem and its proof are intuitive; the second concerns cases in which the content of the theorem is non-intuitive but its proof is intuitive; the third, cases in which the content is intuitive but its proof is not.

56An example of the first is Triangle inequality. It seems reasonable to think that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. The proof is intuitive in that it just requires a geometrical construction that can be easily pictured.

57An example of the second kind is, we argue, Cantor’s theorem, which does not seem intuitive because it entails the existence of different degrees of infinity. Nonetheless, its proof is intuitive in that it is linear and very easy to grasp as a unity. In other words, the proof is not just a complex composition of different ideas or single steps but could be summed up in a few words. An indirect evidence of its intuitiveness is the application of similar diagonal arguments in other fields of mathematics, such as the theory of computation and proof theory.¹⁷ Another example is Cantor’s rejection of the universal set. Intuition suggests its existence. Indeed, it is quite easy to be defined, and it is clear what it has to count as its members, i. e. everything. However, the proof of its non-existence is trivial because it directly follows from Cantor's result according to which a set always has a smaller cardinality than its power set. Other cases of non-intuitive results with intuitive proofs are paradoxes. Indeed, paradoxes just are intuitive arguments that prove results that are not only non-intuitive but even counterintuitive¹⁸.

58An example of the third case is the infamous proof that 1 + 1 = 2, provided in Russell and Whitehead’s Principia Mathematica. Of course, the content is so intuitive that it was generally considered self-evident. Yet, Russell and Whitehead’s proof takes many pages and uses a quite heavy formalization. For this reason, Poincaré famously claimed that logicists were proving an obvious statement by a far from obvious proof.¹⁹ Someone could object that, in the case of 1 + 1 = 2, we have an intuitive proof based on calculation. To deal with this objection, let us consider another example. Take the fact that real numbers are continuous, that is they are ordered without gaps. This property has a clear intuitive appeal based on the geometrical interpretation of the real numbers as points on a line. However, to prove it, we need a formalization of real numbers through Dedekind’s Cuts and other subtle concepts of Real Analysis.²⁰

59Of course, we also have cases in which both the content of the theorem and its proof are non-intuitive. This is the case of, for instance, the theorem of classification of finite simple groups which spreads out over many journal articles. However, such cases do not count as intuitive at the first place. We let them therefore out of our taxonomy of non-immediate phenomenological intuitions which can be summarized as follows:

60In what follows, we will consider how recent literature deals with intuition regarding inferential objects. In particular, we will point out what we argue to be some problems of the accounts proposed and try to figure out some solutions.

4.2 Relations between intuitiveness of theorems and proofs

61Recent literature deals with intuitions regarding inferential objects. However, these attempts miss the taxonomy we have just proposed. In other words, it is quite common for philosophers to conflate the intuitiveness of theorems with that of their proofs.

62In what follows, we will consider (Koksvik, 2013)’s position and (Chudnoff, 2020)’s refinement of such a position.

4.2.1 The intuitiveness of the proof is constitutive of that of the theorems

63In (Koksvik, 2013), the author argues convincingly that intuition can regard results of conscious reasoning such as logical and mathematical theorems. To exemplify his position, he considers De Morgan’s laws.²¹ In particular, he seems interested in the intuitiveness of these laws as it comes from the availability of their proofs. The author is not explicit regarding whether such proofs have to be considered intuitive. However, since they have the role of making theorems intuitive, it seems plausible to claim that this is the case. Hence, we can argue that Koksvik’s account concerns, above all, cases in which the content of some theorems is intuitive because of the intuitiveness of their proofs.

64Chudnoff refers to Koksvik and proposes an example that is, we argue, more interesting than Koksvik’s. Indeed, while Koksvik seems to limit himself showing that some theorems are intuitive in that their proofs are intuitive, Chudnoff analyzes a more complex case, namely that in which a non-intuitive theorem has both a non-intuitive and an intuitive proof. The comparison between such proofs allows him to show how the intuitiveness of the proof can quite uncontroversially be constitutive of the intuitiveness of the theorem. Let us see the case in detail.

65The theorem in question asserts the existence of a curve that touches all the points of a plane. This theorem was originally proved by Peano²². Both the theorem and Peano’s proof are non-intuitive. Indeed, we cannot visualize the curve, and the proof provides no idea of what it could be like. As Chudnoff points out, there is another way to prove the theorem, that is by Hilbert’s constructive proof. The theorem is the same and so is, of course, non-intuitive. By contrast, Hilbert’s proof is intuitive in that, even though it does not allow to visualize the curve, it gives a clear idea of how it could be like by providing an infinite-step process whose starting point can be visualized, and the passage from one step to the next one is intuitive.

66Thus, Chudnoff provides a more refined argument for Koksvik’s position. Indeed, the intuition used by Hilbert gives us clues concerning the content of the theorem. That is, the former makes the latter intuitive, or — at least — more intuitive than before.

67Koksvik’s thesis can be supported also by considering other cases. Take for instance the intermediate value theorem formulated above. The content of the intermediate value theorem is intuitive. Its intuitiveness just follows from basic geometrical insights. However, in intuitionistic mathematics, it cannot be proved.

68Now, what is shown by the fact that the intuitionist rejects the proof? Of course, the opponent of intuitionism will argue that the theorem, even if not provable in intuitionistic mathematics, is still intuitive and so that intuitionism fails to account for such a mathematical fact. However, another — and, we argue, more interesting — interpretation is available.

69The interpretation goes as follows: it is the intuitionistic conception of real numbers as objects (to some extent) in fieri that makes the intermediate value theorem not intuitive at all, and so our prima facie intuition about the truth of the theorem rests on the assumption of real numbers as fully given, that is by some intuitive presuppositions of the proof. To be more specific, the main reason why the intuitionist rejects the intermediate theorem value is that, since the comparison of real numbers requires the comparison of infinite objects, she cannot prove that real numbers are totally ordered by <. In other words, we have no constructive ground for saying that for each pair of real numbers a and b, a<b, a>b or a=b.

70Hence, generalizing this point, we can conclude that this fact suggests that Koksvik and Chudnoff are right, at least in certain cases, in claiming that the intuitiveness of the theorem is given by some particular assumptions that can be found in the proof.

71 Another — even more extreme — example is the intuitionistic theorem according to which all the functions defined in an interval are continuous in that interval. This theorem is incoherent with classical real analysis. Indeed, it is easy to find examples of non continuous functions defined over an interval [a, b]. To see how, take point c in the interval [a, b] and take two functions f and g continuous in [a, b] such that f(c) is different from g(c). Now, the non-continuous function h defined in all [a, b] is given by h(x) = f(x) if a ≤ x ≤ c and by h(x) = g(x) if c < x ≤ b, where c is the point of non-continuity.

72However, the intuitionist does not accept the example because she cannot prove that h(x) is defined at each point of the interval. The reason is that intuitionism does not allow us to prove that real numbers are totally ordered. Hence, for the intuitionist, the existence of non-continuous functions defined over some intervals is not intuitive.

73Here the situation is more extreme than the case of the intermediate value theorem because it seems that the intuitionists do not only reject something intuitive but prove something that is barely counterintuitive, that is the non-existence of some objects whose examples are available. Of course, it can be said, as before, that intuitionism has non-intuitive consequences. But, once again, it can also be argued that the intuitionist is right in supporting that the intuitiveness of the theorem in question derives from that of its proof.

74In particular, the existence of non-continuous functions seems intuitive for the same reasons that make the intermediate value theorem intuitive.²³ Generally speaking, both theorems show that, even if the statement of a theorem seems intuitive, this intuitiveness rests on the intuitiveness of its proof and basic principles. Should we conclude that for all intuitive theorems, Koksvik’s analysis applies, and that their intuitiveness is due to that of their proofs? In the next section, we will argue that this is not the case.

4.2.2 The intuitiveness of the proof is not constitutive of that of the theorems

75The previously mentioned cases show that Koksvik’s account of intuitiveness for proof and theorems is stimulating. We argue nonetheless that it cannot be regarded as the whole story. Indeed, not all the non-immediate phenomenological intuitions fit this schema. And this becomes clear by just reconsidering our taxonomy above which presents cases of intuitive theorems having non-intuitive proofs such as the continuity of real numbers.

76But of course these are not the only cases in which the intuitiveness of the theorem is not given by that of its proof. We can have cases of non -intuitive theorems having intuitive proofs whose intuitiveness is nonetheless not given by that of the proof. This is the case of paradoxes that persist in their non-intuitiveness even when they are corroborated by intuitive proofs.²⁴ Moreover, we have cases of intuitive theorems with intuitive proofs whose intuitiveness is not given by that of the proof. It is indeed, for instance, hard to affirm that Triangle Inequality is intuitive because of its proof. Generally speaking, some theorems seem intuitive even before the proof has been spelled out.

77Hence, we have cases in which the intuitiveness of the theorem and that of the proof are, so to say, independent of each other. In other words, it is not always the case that the intuitiveness of a theorem is provided by that of its proof. Sometimes, it depends upon the statement of the theorem itself.

4.2.3 Usefulness of non-immediate phenomenological intuitions

78In the previous subsections, we have investigated the relations between the intuitiveness of the proof and that of the theorem. In this section, we will investigate what is the purpose of intuitiveness for theorems. In particular, we will ask whether non-immediate phenomenological intuitions have a justificatory role.

79Here is the main question: why the intuitiveness of a theorem and that of the proof are supposed to be useful given that proofs already provide conclusive justification?

80Even in Koksvik’s and Chudnoff’s cases, the question is pertinent. Since a theorem is proved, what is added by knowing that its intuitiveness is given by that of its proof?

81On the one hand, we could claim that, following Koksvik’s and Chudnoff’s suggestions, the fact that mathematicians are usually not satisfied with non-intuitive proofs and struggle to find intuitive and elegant ones seems to speak in favor of the relevance of intuition for justification. On the other hand, once a given sentence has been proved (and so becomes a theorem), intuition seems to lose its justificatory role. In other words, if a theorem is proved, there seems to be no more job for intuition to do.

82To use, once again, Chudnoff’s example, it seems that we gain something when we prove the existence of the curve that touches all the points in the plane using Hilbert’s methodology instead of Peano’s. But since both proofs are conclusive, the same question arises again: what intuition is supposed to add? Here are some proposals.

a) Plurality of justifications is useful

83It can be argued that there is nothing strange in having a plurality of justifications for the same sentence, and that this plurality is even useful. As an example, I could know that "I have left my keys in the garage" because I am seeing them there, because I remember that I left them there, because someone reliable told me so, etc. I could be aware of all these justifications at once, and each of them could be relevant for me to believe the sentence. This abundance of epistemic roots to justify "I have left my keys in the garage" is useful because if one of these lacks, we still have the other in place. This is warranted by the fact that all these justifications are independent of each other. I can for instance be fully justified in believing that the sentence is true just by memory, or alternatively by vision, and so on.

84However, Koksvik’s and Chudnoff’s cases do not fit this schema. Following the previous example, the justification for the existence of the curve that touches all the points in the plane is, so to say, “grounded” on its proof. That is, we cannot know that the theorem is true without having its proof. Hence, plurality of justifications seems to be, in the cases in which the intuitiveness of the theorem comes from that of the proof, totally useless.

b) Koksvik’s reply: plurality of justifications increases the degrees of justification

85Koksvik does not directly face the problem of the plurality of justifications in the way we have just treated it. Nonetheless, he focuses on the question of knowing whether and how the intuitiveness of the theorem, understood as sharing the phenomenological features of intuition, justifies the theorem itself.

86To reply, he proposes that such a justification goes by degrees and so that intuitiveness just raises such degrees by providing “additional justifications” to the theorem. This solution seems acceptable, and also independent of his position according to which the proofs make the theorems more intuitive. Hence, his proposal could be extended to those non-immediate phenomenological intuitions that are independent of the intuitiveness of the proof.

87However, there are some difficulties that the author seems to ignore. To get this point, consider what should happen according to his theory when we prove something counterintuitive. If the intuitiveness of theorems provides additional justification, counterintuitive theorems should receive a less stringent justification than intuitive ones. However, results such as Einstein’s relativity of simultaneity and Banach-Tarski theorem²⁵ could hardly be regarded as less secure than intuitive results such as the continuity of real numbers. This seems to argue against Koksvik’s idea that intuition has epistemic weight also about proved sentences and, more specifically, that the intuitiveness of a theorem raises its degree of justification.

88Another interesting example shows that intuition of a theorem (or, more generally, of a result justified by other means) can have an epistemological role that is completely extraneous to degrees of justification.

89Take classical logic. The choice of its axioms is, to some extent, conventional. Indeed, classical logic presents a lot of possible independent axiomatizations. Now, for someone endorsing intuition as a reliable faculty, it should be a good norm to adopt axioms that are intuitive. This will inevitably lead to proving both other principles that could be regarded as intuitive and principles that are less intuitive. Classic examples of the latter are paradoxes concerning the material conditional.

90Now, intuitive theorems formulated following a given axiomatization for classical logic can become intuitively justified axioms in alternative axiomatizations for the same logic. Thus, if we have the intuitiveness of the proved results, then we also have different possible starting points for our theory, all of which are justified by intuition. The epistemic role of those intuitions that regard proven results has nothing to do with extrajustification. This fact shows that, as anticipated, Koksvik’s characterization of the role of non-immediate phenomenological intuition is too narrow.

91Another interesting case showing that Koksvik’s thesis is problematic can be spelled out. This case regards intuition in philosophy. To figure it out, we propose to consider Fine’s infamous account of Ontological Dependence.²⁶ The author characterizes dependence using essence. What he proposes is that

[...] we may take x to depend upon y if y is a constituent of a proposition that is true in virtue of the identity of x or, alternatively, if y is a constituent of an essential property of x.27

92To check this definition, he evaluates whether the account entails some strange consequences, as for instance the fact that Socrates would depend upon the number 2. Now, of course, this cannot intuitively be the case. That is, we have a strong intuition that Socrates does not depends on the number 2.

93However, to definitely be able to assure this fact as a point of his theory, Fine cannot only rely on intuition. He has to prove that his favored definition of dependence does not entail the previous unintuitive result. More than this. He has to prove that the account rather entails its rejection.

94To show this, he argues by cases and distinguishes between two kinds of essence: constitutive essences which come from the nature of the objects in question (for instance, Socrates is a human being), and consequential essences which are logical consequences of constitutive essences (for instance, Socrates is a human being or a whale).

95Following the definition of dependence above, it is easy to see that, according to Fine, constitutive essences are those that give rise to ontological dependence. Constitutive essence of things let us also know that some given properties have nothing to do with the nature of the object in question. Following the previous example, if we have access to Socrates’ constitutive essence, we know that number 2 is not one of his constituents. Then, the first cannot depend upon the second. That is, Socrates does not depend upon the number 2. This fact follows from some intuitions plus Fine’s basic principles concerning the relation between essence and ontological dependence.

96However, it is not clear whether we always have direct access to constitutive essences. Fine proposes then a way to exclude cases of unintuitive dependence also when we have access only to consequential essences. A specific example was the dependence of Socrates upon the number 2. Indeed, “2 = 2” is a logical consequence of Socrates’ essence. Fine’s solution is to point out that the term “2” can be generalized away: It can be substituted by any other term. He argues that, for this reason, it cannot occur in Socrates’ essence, and so that there is no ontological dependence of Socrates upon it.

97Now, in both these cases, the sentence “Socrates does not depend upon the number 2” is justified inferentially. It follows from the basic principles of Fine’s theory of essence and ontological dependence. However, the sentence was already justified directly by intuition, and the theory has been intentionally developed in order to prove it. The moral is then that it would be absurd to claim that these justifications increase the degree of justification of this sentence. Hence, internal formal derivation and external justification by intuition have radically different epistemological purposes.

98To better see why, compare the case with that of Newtonian physics. The degree of justification of the sentence “all bodies fall with the same acceleration, regardless of their mass” is not increased by its formal derivation from the basic laws of Newtonian physics. This is instead an observational fact that Newtonian physics was intentionally formalized to prove. In other words, the justification of “all bodies fall with the same acceleration” does not go from Newton’s physics to the observation that all bodies fall with the same acceleration. It rather goes the other way around. Similarly, the justification of “Socrates does not depend upon the number 2” does not go from Fine’s theory to the intuition that “Socrates does not depend upon the number 2” but the other way around.

99To sum up, when the conclusion of a proof can be also directly justified by intuition, this faculty could provide something more than extra justification. Indeed, in general, derivation and intuition have different epistemological roles. The first takes place inside a formal theory, while the second regards the reliability of the formal theory itself.

c) The intuitiveness of the proof is epistemically useful because it provides flexibility

100Let us now focus, once again, on the intuitiveness of the proof. Also in this case, Koksvik’s account seems at best partial. Indeed, if intuition provides the justification for inferential rules and basic axioms employed in the proof, the mere fact that the proof is built up from these building blocks is enough to prove that the conclusion is true. Moreover, this argument for the truth of the conclusion of a sound proof seems so simple to be intuitive. As a consequence, even for an exaggeratedly long and non-intuitive proof, an intuitive argument still warrants the truth of its conclusion. Hence, the intuitiveness of the proof of a theorem seems unneeded as justification for its truth.

101However, there is another way in which intuitive proofs could be preferable to non-intuitive ones. Indeed, the possibility of grasping a proof in its entirety makes it much more flexible and adaptive. An intuitive proof, even when discovered to be non-conclusive, can generally be modified to prove other theorems. We have already seen the example of diagonalization in the previous sections. Diagonalization has applications outside of set theory in which it was developed.

102Another even more interesting case is investigated by Lakatos in his famous work (Lakatos, 1976), where he considers Euler’s theorem which states that the number of vertices, edges, and faces of a polyhedron are linked by the following relation:

103V – E + T = 2

104Lakatos provides a very intuitive proof of this result. Then, he proposes some counterexamples. Since the proof is intuitive and employs a strikingly fertile methodology, both the proof and the results can be adapted to cover the counterexamples to arrive at the definition of Euler characteristic, a very important concept of topology.

105Generally speaking, what Lakatos is mainly interested in is how proofs can be reshaped by the discovery of counterexamples, and especially in demarcating fruitful reactions to such discoveries from unfruitful ad hoc ones.

106But let us now take a step back and argue that this proof was well-suited for this investigation specifically because of its intuitive appeal. While soundness assures the truth of the proof, intuitiveness makes it possible to understand why the proof is sound. This does not provide extra justificatory power but makes the proof much more flexible. It can be modified and applied to other fields, or modified to solve some issues which are found in the proof itself. In some way, we could say that intuition of the correctness of the proof makes sense of its truth, while a non-intuitive proof provides a conclusive justification that is unable to make sense of the result in the same way.²⁸

107To sum up, an intuitive proof is more useful than a non-intuitive one in that it is more versatile and flexible. So, even though, as we have seen, intuition does not give extra justificatory power to proofs, the research of intuitiveness is nonetheless not a mere aesthetic interest for mathematicians. In 5.2.3, we have investigated what intuition adds to theorems and proofs. We have evaluated different alternatives. In a) and b), we have focused on intuition about theorems. In c), we have focused on intuition about proofs. More specifically, in a), we have proposed that intuition justifies theorems alongside proofs so that if some errors are found in the proof, intuition still warrants the result. This proposal can at most be partial and does not apply to the cases in which the intuitiveness of the theorem derives from that of the proof, such as Koksvik’s and Chudnoff’s examples. Then, in b), we have considered Koksvik’s and Chudnoff’s proposals according to which intuition raises the degree of justification of a sentence. We have observed that this assumption leads to implausible consequences when used to evaluate counterintuitive but well-established theorems. Moreover, we have proposed other roles for the intuitiveness of theorems and inferentially proved results that seem more relevant for the epistemology of mathematics and philosophy. Finally, in c), we have dealt with intuition regarding proofs. We have argued that intuitiveness is not required for a proof to be sound and conclusive. As a consequence, intuition neither raises the degree of justification of a proof nor makes it more reliable. However, the intuitiveness of a proof is fundamental when we have to adapt the proof to suit other applications or solve some alleged objections.

5. Conclusions

108In this paper, we have proposed a taxonomy of intuitions. In particular, we have argued that intuitions can be distinguished into epistemic and phenomenological.

109Epistemic intuitions concern axioms and, more generally, starting points of epistemic enterprises. It has therefore to have a justificatory power. We have also argued that epistemic intuitions further distinguish between immediate and non-immediate. Examples of the first are MP and transitivity of identity; examples of the second are the intuition that there is a Universal Set and CP.

110Phenomenological intuitions regard instead the main features of intuition. Classically, intuition is presentational, pushy, and forceful. Phenomenological intuitions cover all cases of epistemic intuitions plus all intuitions which have the features in question but that are not basic principles. The first kind involves cases of immediate phenomenological intuitions, and the second of non-immediate phenomenological intuitions. Examples of the first are CP and MP; examples of the second are Pythagoras’ theorem and intermediate value theorem.

111Then, we have focused on phenomenological non-immediate intuitions and further distinguished between phenomenological non-immediate intuitions concerning theorems and phenomenological non-immediate intuitions concerning their proofs. More specifically, we have considered Koksvik’s and Chudnoff’s positions according to which intuitiveness of the proof is constitutive of that of their theorems. We have argued that we have good reasons to endorse their position but also that we have cases in which it fails.

112Finally, we have discussed whether intuition still has epistemic appeal even when its content are theorems that have a proof. We have considered Koksvik’s reply according to which intuition increases the degree of justification. We have argued that this thesis is problematic for different reasons. It does not account for cases in which a well-established theorem is counterintuitive, and it neglects other relevant epistemic roles of intuition.

Bibliographie

Notes

To cite this article

About: Leonardo Ceragioli

About: Valentina Luporini