- Home
- Volume 13 (2017)
- Numéro 2: L'acte d'imagination: Approches phénomén...
- Les mathématiques comme logique de l’imagination : Une proposition leibnizienne et son actualité
View(s): 4064 (7 ULiège)
Download(s): 755 (1 ULiège)
Les mathématiques comme logique de l’imagination : Une proposition leibnizienne et son actualité

Résumé
Dans cet article, je me propose de remettre en avant une proposition de Leibniz caractérisant les mathématiques comme « logique de l’imagination ». Après avoir rappelé le sens de cette proposition ancienne, dont on trouve également des traces chez Descartes, j’entreprends d’en montrer l’actualité à l’aide d’exemples tirés de la pratique mathématique actuelle. L’enjeu principal de l’article est de prendre à revers une vue très répandue, mais rarement justifiée, selon laquelle l’usage de pratiques « symboliques » constituerait une rupture par rapport à une pratique supposée plus ancienne, voire archaïque, dans laquelle les mathématiciens s’appuyaient plus sur l’imagination. Revenant au débat entre Leibniz et Descartes sur la question de la « connaissance symbolique », j’essaye de montrer qu’il n’en est rien et que la connaissance symbolique est une forme de la « logique de l’imagination » plutôt qu’une alternative.
Table of content
Introduction
1Cet article voudrait promener son lecteur dans des mondes « imaginaires » et pourtant très rigoureusement « logiques ». Ces mondes, ce sont ceux de la mathématique. Non qu’il s’agisse de décrire, comme cela a été fait tant de fois, les espaces nouveaux que dessinent pour nous les mathématiciens et qui forment autant de structures de mondes alternatifs au nôtre. Non qu’il s’agisse non plus d’évoquer les trésors d’imagination qu’ils doivent déployer pour la solution de leurs problèmes, comme tous les autres scientifiques créateurs. L’imagination dont il s’agira ici ne sera pas seulement celle qu’on gagne à construire des espaces et des temps différents du nôtre, mais plus généralement celle qui se déploie dans toute représentation mathématique, aussi simple soit-elle. L’idée de relier mathématique et imagination est souvent associée de nos jours aux positions d’Emmanuel Kant, mais c’est en fait une idée très ancienne, formulée dès l’Antiquité, pour rendre compte de la manière dont on raisonne en géométrie avec des diagrammes1. Cette tradition s’est développée jusqu’à l’âge classique où elle a pris un tour nouveau avec les pensées de Descartes et de Leibniz. Pour la première fois, en effet, il s’agissait d’associer le travail de l’imagination à une sphère bien plus large que celle des dessins du géomètre (ou de leur contreparties idéales) : celle des symboles. C’est cette tradition que j’aimerais rappeler ici et poursuivre.
2L’expression « logique de l’imagination » (logica imaginationis) surgit au détour d’un texte de Leibniz consacré à la mathesis universalis, mais d’autres passages du philosophe mobilisent une idée similaire pour caractériser plus généralement les mathématiques dans leur ensemble. Le développement des mathématiques symboliques avait, en effet, permis de remettre en avant cette idée ancienne, de préférence à la définition qui voyait les mathématiques comme simple science de la quantité (une définition que Leibniz juge trop restrictive dès lors que le calcul peut s’étendre à d’autres choses que des quantités). Elle n’en est pas moins surprenante au premier abord. Nous n’avons pas l’habitude de voir associer l’idée de mathesis universalis à un recours à l’imagination2. C’est même aller directement contre une certaine image de la naissance de notre modernité, supposément portée par l’idée de mathesis universalis, qu’on associe à la fin d’un certain rôle de l’imagination en mathématiques, au développement de pratiques purement « symboliques », voire » formelles », dont les prémices seraient à trouver dans le développement d’une algèbre littérale à la Renaissance et qui seraient l’instrument prédestiné d’une géométrie devenue « analytique » et d’une science de la nature devenue mathématisée. C’est pourquoi il est aujourd’hui nécessaire de revenir sur cette histoire. Ce sera l’objet de la première partie de cet article dans lequel j’essayerai de faire revivre les propositions et les discussions de Descartes et de Leibniz à ce sujet. Dans la seconde partie, je voudrais indiquer que la remise au premier plan de l’imagination n’est pas une simple question de fidélité historique et de meilleure compréhension de pratiques du passé (même si elle l’est également !). Elle ouvre, en effet, des questionnements qui s’appliquent tout aussi bien aux mathématiques les plus contemporaines — questionnements que le mythe du « formel » comme lieu de transparence du concept à lui-même a malheureusement écrasés. En m’appuyant sur quelques exemples élémentaires, tirés de diverses parties des mathématiques, j’essayerai de montrer en quel sens on peut encore tenir aujourd’hui pour féconde la proposition leibnizienne : les mathématiques sont une « logique de l’imagination ».
1. Logica imaginationis
3« La Mathesis Universalis doit présenter une Méthode de détermination exacte pour ce qui tombe sous l’imagination. Elle est, pour ainsi dire, une Logique de l’imagination »3. Ainsi s’exprime Leibniz dans l’un des projets qu’il entreprend d’élaborer dans les années 1680 pour donner de « nouveaux éléments » de « mathématique universelle ». Son idée est que cette caractérisation est le meilleur point de vue si l’on veut espérer aller plus loin que Descartes dans sa description de la mathesis universalis et l’étendre de la quantité, où ce dernier l’avait cantonnée, vers le royaume de la qualité — un mouvement que le développement de calculs symboliques avait rendu naturel. Comme j’aurai l’occasion de l’expliquer plus avant par la suite, Leibniz ne voit pas pour autant cet élargissement comme une rupture de continuité et considère plutôt cette proposition comme une extension de la proposition cartésienne.
4Le lien des mathématiques à l’imagination est également posé à la même époque dans le De ortu, natura et progressu algebrae :
L’Algèbre, cependant, ne semble pas devoir être confondue avec la Mathesis Universalis. Certes si la Mathesis traitait de la seule quantité, c’est-à-dire de l’égal et de l’inégal, de la raison et de la proportion, rien n’empêcherait l’Algèbre (qui traite de la quantité de façon universelle) d’être tenue pour sa partie générale. Mais à la vérité, il semble que tombe sous la Mathesis tout ce qui tombe sous l’imagination en tant que distinctement conçu. Par conséquent, on y traite non seulement de la quantité, mais aussi de la disposition des choses. Il y a ainsi deux parties, si je ne me trompe, dans la Mathesis generalis : L’Art combinatoire [qui traite] universellement de la variété des choses et des formes, c’est-à-dire des qualités de façon universelle, en tant qu’elles sont soumises à un raisonnement distinct, et du semblable et du dissemblable, et la Logistique ou Algèbre [qui traite] de la quantité de façon universelle4.
5On remarquera que le lien à l’imagination n’est pas ici restreint à la théorie universelle, mais s’étend plus généralement à tout ce qui relève des mathématiques. C’est parce que les mathématiques traitent en général de ce qui tombe sous l’imagination (en tant que soumis à des raisonnements distincts) que leur partie universelle peut être désignée comme une logica imaginationis. C’est aussi pour cette raison que Leibniz ne considère pas faire rupture en mettant en avant cette caractérisation : elle décrit la connaissance mathématique elle-même et non une volonté de la réformer. Dans des textes contemporains, il définit d’ailleurs les mathématiques tout simplement comme « la science des imaginables »5. Que cette position ait persisté tout au long de son œuvre est attestée par un passage célèbre de la grande lettre à Sophie Charlotte de 17026. Il présente en outre l’intérêt de donner plus de détails sur la théorie de la connaissance dans laquelle elle prend sens :
Il faut rendre cette justice aux sens qu’outre ces qualités occultes, ils nous font connaître d’autres qualités plus manifestes, et qui nous fournissent des notions plus distinctes. Et ce sont celles qu’on attribue au sens commun, parce qu’il n’y a point de sens externe auquel elles soient particulièrement attachées et propres. Et c’est là qu’on peut donner les définitions des termes ou mots qu’on emploie. Telle est l’idée des nombres, qui se trouve également dans les sons, couleurs, et attouchements. C’est ainsi que nous nous apercevons aussi des figures qui sont communes aux couleurs et aux attouchements, mais que nous ne remarquons pas dans les sons. Quoiqu’il soit vrai que, pour concevoir distinctement les nombres et les figures mêmes, et pour en former des sciences il faut venir à quelque chose que les sens ne sauraient fournir, et que l’entendement ajoute aux sens.
Comme donc notre âme compare (par exemple) les nombres et les figures qui sont avec les couleurs, avec les nombres et les figures qui se trouvent par attouchement, il faut bien qu’il y ait un sens interne, où les perceptions de ces différents sens externes se trouvent réunies. C’est ce que l’on appelle l’imagination,laquelle comprend à la fois les notions des sens particuliers, qui sont claires mais confuses, et les notions du sens commun, qui sont claires et distinctes. Et ces idées claires et distinctes qui sont sujettes à l’imagination, sont les objets des sciences mathématiques7.
6Nous retrouvons ici, au premier abord, une théorie d’ascendance aristotélicienne qui avait largement circulé dans les commentaires au De Anima, et qui posait un lien étroit entre imagination et sens commun. Son ressort premier est le fait que des formes comme le nombre ou la figure ne paraissent pas reconnues perceptivement par l’intermédiaire d’un unique sens privilégié. Je peux voir cinq moutons comme je peux entendre cinq sons ou toucher cinq pommes, de même que je peux reconnaître une forme sphérique aussi bien par la vue que par le toucher8. Mais le point clef pour Leibniz, ici plus platonicien qu’aristotélicien, est que ces formes ne paraissent soumises à des conceptions distinctes que par l’intermédiaire de l’entendement qui en règle l’organisation propre : « Il faut venir à quelque chose que les sens ne sauraient fournir, et que l’entendement ajoute aux sens ». L’imagination joue ainsi un rôle intermédiaire, qu’elle gardera encore chez Kant, entre sensible et intelligible, les mathématiques correspondant à la part où elles se soumettent à une forme de connaissance « claire et distincte »9. On trouverait une présentation très similaire dans les Règles pour la direction de l’esprit de Descartes, mais, comme j’aurai l’occasion de le préciser par la suite, ce nouage entre mathématiques et imagination traverse plus généralement l’ensemble de la pensée cartésienne.
7Un point remarquable des développements leibniziens est qu’ils se trouvent formulés dans un contexte de promotion des méthodes symboliques en mathématiques (au titre de l’ars caracteristica), dont on verra qu’elle prolonge effectivement le geste cartésien tout en s’en écartant sur certains points (le rôle précis de la connaissance symbolique)10. La chose est doublement surprenante pour le lecteur d’aujourd’hui : d’une part, l’opposition à la philosophie kantienne des mathématiques, qui a dirigé nombre de positions depuis la fin du xixe siècle, a promu l’image d’un Kant défenseur de l’imagination en retrait par rapport au développement d’une mathématique « formelle », dont Descartes et Leibniz auraient été les premiers héros ; d’autre part, cette vue d’ensemble a soutenu une interprétation, malheureusement très répandue, selon laquelle la défense par ces derniers auteurs du caractère « intellectuel » des mathématiques (disons, pour faire vite, une forme de « platonisme ») et leurs critiques adressées dans ce contexte à un certain usage de l’imagination allaient de pair avec — voire pouvaient être identifiées à — leur défense de méthodes symboliques.
8Ce n’est pas le lieu d’entrer dans le détail de ce tableau dont l’influence sur notre manière de lire les auteurs classiques est si profonde — et, il faut le dire, si néfaste. Qu’on me permette simplement de rappeler quelques déclarations qui en dresseront un rapide tableau d’ensemble, par exemple celle de Husserl au § 26 de Logique formelle et logique transcendantale :
La découverte proprement dite du formel s’effectue pour la première fois au commencement des temps modernes dans la réalisation de la fondation de l’algèbre par Viète, donc de la technicisation déductive de la théorie des nombres et de la théorie des grandeurs ; et cette découverte atteint ensuite son sens pur grâce à Leibniz dont la mathesis universalis a manifestement complètement repoussé toute attache à une généralité quelconque liée au concret, fût-ce la plus haute généralité11.
9Dans la Krisis, juste après avoir exposé le tournant galiléen en science et le rôle joué par l’algébrisation de la géométrie promue par Descartes, il poursuit :
Leibniz a le premier aperçu, précédant du reste de loin son époque, l’idée universelle fermée sur elle-même d’une pensée algébrique au plus haut sens du terme, l’idée d’une « mathesis universalis », comme il l’appelait ; il a le premier reconnu en elle la tâche de l’avenir, alors que c’est seulement à notre époque qu’elle s’est au moins approchée de sa réalisation systématique. Dans la totalité et la plénitude de son sens, elle n’est rien d’autre qu’une logique formelle développée dans toutes les directions (et dont la réalisation, dans la totalité propre à son essence, va à l’infini), une science des formes-de-sens du « quelque chose en général », formes constructibles dans une pensée pure, c’est-à-dire dans une généralité formelle vide12.
10Une description comparable est donnée par Louis Couturat, dans un rapport moins positif à Descartes, mais qui associe néanmoins l’idée de mathesis universalis à la prise de conscience progressive du « caractère formel des raisonnements »13. L’idée générale défendue par ces auteurs, et qui s’est très largement perpétuée jusqu’à nos jours, est que la mathesis universalis marquerait un tournant dans l’histoire des mathématiques et de la philosophie, lié au développement de méthodes symboliques, que Descartes aurait esquissé et que Leibniz aurait amené à son expression la plus haute sous la forme d’une mathématique accédant à sa vraie nature de discipline « formelle »14. Ce faisant, ils auraient l’un et l’autre annoncé de manière prophétique ce que les mathématiques étaient amenées à devenir, croit-on, à partir du milieu du xixe siècle à la faveur de la prétendue « crise de l’intuition »15.
11Un point sur lequel j’aimerais particulièrement insister est que cette lecture a promu une vue de Descartes et de Leibniz dans laquelle les critiques qu’ils peuvent faire l’un et l’autre contre l’usage de l’imagination en mathématiques et leur attachement au caractère intellectuel de cette discipline seraient liés à la défense d’une mathématique « symbolique ». Or on ne trouve nulle trace de cette connexion chez ces auteurs et elle nourrit malencontreusement l’idée, aussi fausse que répandue, selon laquelle le « symbolique » n’était pas pour eux du ressort de l’imagination (voire s’y opposait)16. J’ai déjà rappelé que cette image va en sens contraire de nombre de déclarations de Leibniz. On pourra leur ajouter celle-ci qui relie plus explicitement encore la manipulation des symboles (ou « caractères ») à un travail de l’imagination :
Nous ne pouvons pas facilement juger de la possibilité d’une chose à partir du seul fait que ses réquisits sont pensables, lorsque nous pensons ses réquisits un par un, et que nous ne les joignons pas en un seul. Mais puisque nous ne pouvons joindre des idées différentes en une seule pensée (bien que nous puissions les unir à l’aide de caractères) et représenter tout à fait conjointement une série entière de pensées différentes, nous ne pouvons pas juger de l’impossibilité par la pensée, sauf si nous représentons conjointement les idées singulières. Or ceci ne peut avoir lieu que si nous sentons, c’est-à-dire imaginons conjointement les caractères, ce que l’on fait grâce à des caractères qui représentent les idées dans l’imagination17.
12Descartes s’exprime peu sur le statut gnoséologique des symboles et se contente de les référer à une aide de la mémoire. Cependant, nous ne devons pas oublier que la mémoire est pour lui un prolongement de l’imagination18 autant qu’une aide pour l’entendement19. Surtout, il associe régulièrement et très explicitement, lui aussi, les mathématiques à l’usage de l’imagination20. Outre les passages bien connus des Regulae — dont on pourrait toujours considérer qu’ils sont dépassés par le développement ultérieur de sa mathématique et de sa métaphysique — on pourra rappeler les échanges avec Élisabeth de 1643, où apparaît la déclaration suivante : « Les pensées métaphysiques, qui exercent l’entendement pur, servent à nous rendre la notion de l’âme familière ; et l’étude des mathématiques, qui exerce principalement l’imagination en la considération des figures et des mouvements, nous accoutume à former des notions du corps bien distinctes »21. Cette position de principe se transcrit d’ailleurs dans la pratique par la manière d’affronter les problèmes géométriques, dont Descartes rappelle à la même Élisabeth qu’il les aborde toujours — le mot est de lui — à partir de certaines relations détectées dans les diagrammes22.
13On objectera que les Méditations métaphysiques dressent, quant à elles, un tout autre portrait et nous rappellent, sur l’exemple célèbre du chiliogone, à quel point le recours à l’imagination ne saurait être constitutif en mathématiques. Remarquons néanmoins qu’il ne s’agit pas, en tout état de cause, de promouvoir une nouvelle mathématique, purement symbolique. Dans ce passage des Méditations, comme dans tous les autres passages où il est question de mathématiques dans cette œuvre, il n’est pas question d’équations ou de symboles, mais de triangle, de pentagone, de myriogone. Surtout, une chose est de distinguer pensée pure et imagination (un point sur lequel Leibniz le suivrait sans peine), autre chose de déclarer que nous n’avons jamais besoin d’imagination pour faire des mathématiques. Or on ne prête pas assez attention au fait que l’exemple du chiliogone ne sert pas seulement à montrer que cet objet n’est pas accessible de manière distincte dans les limites d’une imagination directe, et qu’il nous faut alors recourir au soutien du concept — une thèse qui, comme nous le rappelle l’exemple célèbre du « morceau de cire », s’étend en fait à toute chose — ; il est également distingué par Descartes du cas du pentagone où l’imagination et la connaissance conceptuelle sont déclarées évoluer dans un parfait accord23. C’est ce que Descartes redira justement à Élisabeth en 1643, rappelant que « l’âme ne se conçoit que par l’entendement pur » tandis que « le corps, c’est-à-dire l’extension, les figures et les mouvements, se peuvent aussi connaître par l’entendement seul, mais beaucoup mieux par l’entendement aidé de l’imagination »24. Ceci est également cohérent avec les conceptions exposées dans les Regulae, reprises dans la seconde partie du Discours (où Descartes revient allusivement sur son premier calcul géométrique), puis postérieurement répétées dans la correspondance : les critiques que Descartes adresse régulièrement à l’imagination n’ont nullement pour fin de promouvoir une nouvelle mathématique « intellectuelle » (pour Descartes, les mathématiques sont une discipline intellectuelle, indépendamment de toute formalisation) ; elles ont pour but de prôner un usage régulé de l’imagination, ce qui suppose de s’en tenir à des cas où imagination et intellect évoluent dans un strict parallélisme. L’utilisation du symbolisme est présentée non pas comme une manière d’abroger l’usage de l’imagination, mais d’en prolonger le pouvoir par l’intermédiaire d’autres formes de représentation mieux adaptées au travail de mémorisation. Or ces représentations ne sont elles-mêmes, comme y insistera Leibniz, que d’autres manières d’imaginer (et non pas de procéder par « purs concepts », une pratique dont on aurait d’ailleurs du mal à trouver un seul exemple chez le Descartes mathématicien)25.
14Si les deux auteurs s’accordent ici, ce n’est donc pas sur le fait que les mathématiques devraient être débarrassées de l’usage de l’imagination, même s’ils insistent régulièrement sur le fait qu’il faut s’en méfier et ne pas trop la surcharger, mais sur le fait que l’imagination doit toujours rester sous le contrôle de la connaissance « claire et distincte ». C’est également en ce point que leurs chemins vont se séparer. Pour Descartes, en effet, ce contrôle sera assuré si l’on prend garde de ne s’appuyer que sur des intuitions simples, à la fois du côté des objets et des relations fondamentales. Dans le cas des mathématiques, comme il s’en explique dans la seconde partie du Discours, prolongeant le programme des Regulae, il s’agit de se donner comme objets de départ des segments et un certain nombre d’opérations simples, que l’on peut représenter par des schémas géométriques élémentaires. C’est exactement ce qu’il présente aux premières pages de la Géométrie26. Ceci permet de caractériser en retour les objets mathématiques légitimes comme ceux qui sont accessibles par un enchaînement réglé de telles opérations — ce qui correspond géométriquement à la construction des courbes « selon un mouvement continu » (comme ceux que produisent les fameux « compas cartésiens »27). L’écriture symbolique vient simplement à ses yeux enregistrer ces relations fondamentales pour éviter de surcharger l’imagination de premier niveau et permettre de maintenir, dans le déroulement de l’analyse mathématique, un substrat intuitif constant (sa légitimité étant établie d’avoir été instituée par la simple inscription de relations fondamentales elles-mêmes intuitives). Or Leibniz, comme nombre de ses contemporains, rechigne à une telle limitation dans la construction des objets qui revient, de fait, à rejeter des mathématiques tout un pan des techniques infinitaires. Dès que nous faisons intervenir l’infini, remarque-t-il, le critère proposé par Descartes s’avère précaire : ainsi puis-je avoir une connaissance « claire et distincte » de ce qu’est une « unité », de ce qu’est une « addition » d’unités, mais l’addition de toutes les unités n’en sera pas moins un concept contradictoire, « ce dont il y a démonstration »28.
15On ne peut objecter ici qu’il suffit donc de ne pas se risquer sur ces terres dangereuses où règne l’infini mathématique et où notre imagination, comme nos concepts, nous font précisément défaut. Car comme le rappelle Leibniz à Élisabeth, outre que ces nouvelles « analyses » sont particulièrement fécondes pour certains problèmes que Descartes eut lui-même à affronter, notamment suite aux questions de Florimond De Beaune, il dut également s’y aventurer pour délimiter le régime du possible et de l’impossible en mathématiques. C’est typiquement le cas de la quadrature du cercle, dont Descartes affirma à plusieurs reprises qu’elle était hors de portée des techniques algébriques. Ce faisant, il donnait droit de cité à des « idées », qui ne satisfaisaient pas ses propres critères. Car comment pourrait-on avoir une idée « claire et distincte » de la quadrature du cercle s’il s’agit précisément de faire valoir qu’elle n’est pas accessible à de telles idées ? D’où le dilemme dans lequel Leibniz l’enferma : ou bien, nous n’avons pas d’idée d’un tel objet et il est donc insensé de dire qu’elle permet de délimiter ce qui est accessible ou non en géométrie (nous ne pouvons rien en savoir), ou bien nous en avons une idée claire et distincte et c’est donc qu’on peut posséder une telle connaissance d’objets qu’on déclare pourtant… contradictoires. Cette dernière connaissance, on le sait, est celle que Leibniz proposa justement d’appeler « symbolique » ou « aveugle » et dont il fit reproche à Descartes de ne pas avoir vu qu’elle grevait du même coup sa démonstration de l’existence divine29.
16Il s’agit là d’une objection très forte, car elle se transfère immédiatement à toutes les notions « impossibles », voire simplement dont la possibilité demande à être attestée. Or leurusage est très courant en mathématiques, notamment, j’y reviendrai, dès qu’est mobilisé un certain type de raisonnement par l’absurde. Ceci est un nouvel élément à verser à notre dossier dans la mesure où l’imagination intervient ici sous une autre forme familière : celle de situations « imaginaires », « fictives »30. Mais avant de revenir sur la prise que nous donne cette entrée dans la question du rôle de l’imagination en mathématiques, il peut être utile de rappeler que, sous cette forme générale, elle n’a rien de particulièrement lié à l’infini. Il est tout à fait possible, par des moyens finis, de produire des objets impossibles. Leibniz le voit très bien qui mentionne également l’exemple du fameux « décaèdre régulier » (polyèdre convexe à dix faces régulières)31. Certes, on peut encore rétorquer qu’un tel objet ne sera jamais construit et que nous ne le rencontrerons donc jamais si nous nous en tenons à une vue constructive. Mais tout le problème est que nous ne procédons pas ainsi en mathématiques, où il ne s’agit pas toujours de déduire des vérités à partir d’axiomes, mais aussi de trouver des solutions dont la construction ne va pas toujours de soi. C’est bien là le ressort le plus fort de l’objection leibnizienne en tant qu’elle attaque la méthodologie de Descartes non pas seulement sur ses frontières, mais sur son terrain même : à partir du moment où l’on valorise, comme n’a cessé de le faire Descartes, la méthode « analytique », on se place dans un cadre où l’on fait « comme si » la solution du problème était donnée et il est donc possible que cette solution s’avère, pour différentes raisons, impossible32. Le rôle de l’imagination prend ici son sens le plus fort en tant qu’il donne aux représentations une autonomie que le concept ne peut surmonter qu’à les dissoudre, au terme de l’analyse, dans la contradiction. Il faut, en effet, pour commencer la preuve, que la représentation soit acceptable alors même que nous admettrons, à la fin de la preuve, qu’elle ne correspond à aucun concept ou objet. L’imagination n’est donc pas transparente au concept (ou, plus exactement, cette transparence se conquiert sur fond d’aveuglement et d’opacité). Elle n’est pas donc non plus totalement réductible au pur niveau conceptuel33.
17Ce n’est pas le lieu de détailler tous les attendus d’une telle position. Le seul point que j’aimerais mettre en avant ici est le suivant : Leibniz poursuit le geste cartésien en étendant plus clairement le domaine de l’imagination au symbolique, mais contrairement à Descartes il ne pense pas que cette extension aille avec moins d’opacité ou d’ « aveuglement ». Elle est exactement du même type. La caractérisation des mathématiques comme « logique de l’imagination » lui permet précisément de donner toute son ampleur à cet art de découverte (ars inveniendi) que nous déployons dans les mathématiques en travaillant avec des représentations imaginaires et que l’émergence des méthodes symboliques a rendu plus apparent encore. Elle nous offre du même coup une méthodologie pour aborder cette logique : il suffit de porter une attention particulière à ces lieux des mathématiques où la possibilité des objets doit être attestée.
2. Raisonnement diagrammatique, représentation aveugle et imagination
18Comme j’ai déjà eu l’occasion de le développer dans d’autres études, le lien des mathématiques à l’imagination, qu’on discerne chez Descartes et Leibniz, relève d’une tradition ancienne. On trouve, en effet, chez le néoplatonicien Proclus bien des traits communs à nos deux auteurs34. Mais le plus remarquable est certainement le fait que cette perspectivelargement occultée depuis la fin du xixe siècle revienne sur le devant de la scène aujourd’hui en même temps que l’intérêt de la philosophie des mathématiques se déporte des fondements à la pratique. C’est, en effet, un trait frappant de la récente philosophie « de la pratique mathématique » qu’elle s’intéresse beaucoup au rôle de la visualisation et accompagne l’intérêt des logiciens pour les raisonnements dits « diagrammatiques »35. Si les références à Descartes et Leibniz n’y sont pas particulièrement dominantes, on ne peut s’empêcher de remarquer que figurent en place éminente parmi les chercheurs de ce domaine bon nombre de spécialistes de ces auteurs36.
19Pour le cas qui nous concerne, l’exemple le plus parlant est certainement donné par les études sur la géométrie grecque ancienne, accomplies par Ken Manders et Reviel Netz37. L’un et l’autre ont, en effet, insisté sur le fait qu’est tout simplement fausse la conception courante selon laquelle les représentations diagrammatiques sont inessentielles à la géométrie ancienne et se limitent à quelques cas bien connus où les Anciens auraient été incapables d’expliciter certaines propriétés du continu géométrique dont ils avaient besoin pour leur démonstration. Ils ont mis en lumière un certain nombre de traits cognitifs portés par les diagrammes et qui ont la particularité d’être remarquablement stables, si bien qu’il est possible de détailler un régime d’inférences qu’ils permettent d’accomplir. Manders a proposé d’appeler certaines de ces inférences portées par les diagrammes en géométrie plane euclidienne « co-exactes » et de les considérer comme évoluant en parallèle avec un régime d’attribution « exacte » portée par le texte. Cette découverte a permis à un de ses élèves, John Mumma, d’élaborer un authentique système logique où l’on utilise ces deux régimes inférentiels en parallèle, donnant ainsi à l’idée d’une « logique de l’imagination » un contenu autrement plus puissant que celui d’une simple métaphore38. Ces études ont ainsi montré non seulement qu’il n’est pas possible de se passer de l’imagination diagrammatique dans la géométrie ancienne, mais surtout que cet usage n’a rien de non « rigoureux » et qu’il est parfaitement possible d’en expliciter la « logique » immanente.
20Un point particulièrement intéressant par rapport à la méthodologie que j’ai esquissée dans la première partie est le rôle que tiennent dans ces reconstructions les figures impossibles. Comme le fait remarquer Manders, les démonstrations par l’absurde nous confrontent à une situation très répandue dans les mathématiques grecques anciennes, où l’on voit que les diagrammes ne peuvent pas fonctionner selon une relation purement sémantique (de type » illustratif »). Cela permet à la fois de court-circuiter nombre de débats traditionnels sur la nature des « objets » mathématiques que ces représentations seraient censées « illustrer », mais aussi de revenir au vrai rôle des représentations mathématiques en tant que porteuses d’inférences :
Nombre de difficultés anciennes sur la nature des objets géométriques et la connaissance que nous en avons proviennent de ce qu’on tient pour acquis le fait suivant : le texte géométrique serait vrai, au sens le plus ordinaire du terme, à propos du diagramme ou d’une contrepartie idéale du diagramme. Or, sans même toucher à ses difficultés, on voit qu’une authentique relation sémantique entre le diagramme géométrique et le texte est incompatible avec la réussite de l’usage des diagrammes dans les preuves par l’absurde : les contextes de reductio ad absurdum servent précisément à assembler un corps d’affirmations qui, de manière évidente, ne peuvent pas être vraies simultanément ; il en résulte qu’aucune situation géométrique ne pourra sérieusement illustrer le fait qu’elles le soient39.
21Reviel Netz insiste également sur cette situation où le diagramme mathématique apparaît à la fois comme l’objet propre du géomètre et, dans le même temps, comme ne pouvant pas servir de représentation à un objet authentique40. De manière très intéressante pour nous, il développe alors une théorie de la fiction (« make-believe ») particulièrement adaptée aux situations où l’on procède par analyse. Sans surprise, un des noms qu’il donne à cette faculté est imagination41.
22Ce n’est pas le lieu d’entrer dans le détail de ces études, auxquelles je me contenterai de renvoyer pour plus de précision. Seul m’importera, pour le moment, le fait qu’elles donnent à l’idée d’une « logique de l’imagination » une actualité frappante. Mais il y a plus, car comme le fait remarquer Manders, l’argument lui-même n’a rien à voir avec les diagrammes géométriques, ni avec une pratique ancienne. Il concerne, en fait, n’importe quelle représentation mathématique que l’on manierait en court-circuitant sa charge sémantique — ce qui est très exactement ce que Leibniz appelle connaissance « symbolique » ou « aveugle ». L’intérêt est alors de nous suggérer que le couplage entre raisonnement et imagination n’a rien de propre à une pratique ancienne, dont on se serait débarrassée avec le développement de mathématiques « rigoureuses ». Si les mathématiques ont évolué vers plus de rigueur à la fin du xixe siècle, ce n’est pas tant en se débarrassant de l’intuition sensible (aucune mathématique n’en est jamais totalement indépendante) que par l’effort qu’elles ont fait de rendre le plus explicite possible (dans le texte) un certain nombre d’inférences autrefois portées par d’autres ressources expressives (dont les diagrammes, mais pas seulement : pensons qu’un des hauts faits du processus de « rigorisation » fut l’explicitation des fondements du calcul différentiel). Mais cela n’a rien à voir, une fois encore, avec le fait de se débarrasser de l’imagination et seule une curieuse conception des écritures symboliques comme « transparentes » aux concepts a pu donner prise à une telle interprétation. Pour le faire entrevoir, suivons la piste évoquée précédemment et prenons un exemple très simple d’analyse géométrique, telle qu’on peut le proposer aujourd’hui aux élèves des écoles42 :
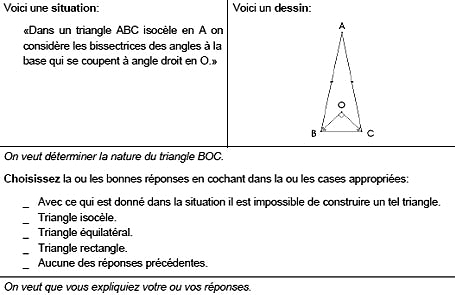
23Dans cet exercice, on veut à la fois vérifier que les élèves ont bien compris certaines propriétés fondamentales du triangle en géométrie euclidienne, comme le fait d’avoir la somme de ses angles égale à deux droits ou le fait pour un triangle isocèle d’avoir ses angles à la base égaux. Mais on veut également apprendre aux élèves à se méfier des constructions géométriques puisqu’il est tentant de répondre trop vite, espérant grappiller quelques points, que le triangle BOC est évidemment rectangle puisqu’il a été construit comme tel. Une analyse de la situation indique qu’un tel triangle est en fait impossible. Par construction, le triangle intérieur est isocèle, ses angles à la base étant égaux (puisqu’ils sont la moitié d’angles égaux), et il est également supposé rectangle. Ses angles à la base doivent donc être de 45 degrés si l’on veut que la somme totale des angles soit de 180 degrés. Mais dès lors, ils ne peuvent être la moitié des angles de BOC qui seraient, si c’était le cas, droits ! Comme le dit Netz de manière savoureuse : minuit sonne à la fin de l’analyse et le carrosse se transforme en citrouille43.
24Le point qui me semble le plus important dans cet exemple, outre qu’il nous familiarise sur un cas très simple avec ce que peut être la « logique de l’imagination » comme ars inveniendi (nous venons, au passage, de découvrir un théorème sur les conditions d’inscription d’un triangle isocèle sur la base d’un autre triangle isocèle), est qu’il est formulé dans le cadre de la géométrie euclidienne telle qu’on la connaît aujourd’hui — c’est-à-dire dans une formulation où il est possible de caractériser l’ensemble de ses principes fondamentaux à l’aide d’axiomes et sans aucun recours à des dessins. On peut faire toute la démonstration qui précède en ne traçant aucune figure et en imaginant simplement la situation (que cette imagination soit visuelle ou non étant laissé indifférent). Il ne s’agit pas là d’une pratique ancienne, mais de la manière la plus ordinaire de faire de la géométrie élémentaire, aujourd’hui comme hier.
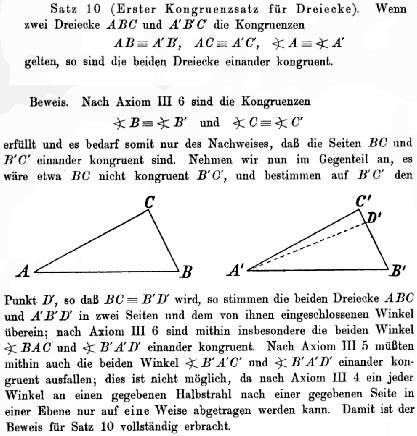
25Comme nous l’a indiqué l’exemple de Manders, ce type de situation est très commun puisqu’il va se retrouver dans nombre de démonstrations par l’absurde (où il s’agit de s’imaginer une situation dont on va ensuite montrer qu’elle est impossible). Si l’on n’est pas convaincu que l’exemple précédent soit parfaitement « rigoureux » (il existe, en effet, des acceptions très variées de la « rigueur » mathématique et peut-être certains rechigneront-ils à accepter que ce que l’on enseigne au lycée soit des mathématiques « rigoureuses »), on pourra aller regarder dans le maître ès rigorisation de la géométrie que fut le mathématicien David Hilbert. Si nous ouvrons l’ouvrage où il a proposé de donner une version purement axiomatique de la géométrie euclidienne, les Grundlagen der Geometrie de 1899, nous constaterons alors que la toute première démonstration du tout premier théorème sur la congruence des triangles qu’il donne se fait… par l’absurde. Ayant défini la congruence de deux triangles par le fait d’avoir leurs côtés et leurs angles congruents, Hilbert entend démontrer qu’il suffit en fait d’avoir deux côtés et l’angle qu’ils comprennent congruents. La preuve se ramène à la démonstration de congruence des troisièmes côtés respectifs de chaque triangle. Pour cela, Hilbert suppose qu’ils ne sont pas congruents. Il « construit » alors sur le troisième côté un point D’, distinct de C’ par hypothèse, et vérifiant la congruence (les guillemets s’imposent du fait que cette « construction » va s’avérer impossible). Il vérifie alors sans mal que l’on se retrouve avec deux angles B’A’C’ et B’A’D’ qui doivent, par hypothèse, être à la fois congruents et distincts, ce qui est impossible en vertu de son axiome III, 4 qui stipule qu’un angle déterminé ne peut être tracé sur une droite en un point que d’une seule façon44 :
26Comme l’avait fait remarquer Manders dans le passage que nous avons cité, cette situation où l’on exhibe une représentation dont on montre ensuite qu’elle n’est pas possible, n’a rien à voir avec l’usage des diagrammes géométriques per se. Elle s’étend immédiatement à n’importe quelle représentation symbolique dans laquelle on utiliserait un raisonnement par l’absurde ou, plus généralement, où l’on ferait une analyse dont le résultat dépendrait de certaines conditions de possibilité. En voici, à nouveau, un exemple très simple, que je tire volontairement de l’algèbre dite « abstraite ». Pour la commodité du lecteur, je le décrirai en langage naturel. On appelle anneau une structure algébrique formée par un ensemble muni de deux opérations qui se comportent comme l’addition et la multiplication ordinaires45. On dit qu’il est intègre s’il ne contient pas de diviseurs de zéro (les diviseurs de zéro sont des éléments a, b, non nuls tels que a*b = 0, en notant la multiplication de l’anneau par *). On dit, par ailleurs, qu’un anneau est un corps si tous ses éléments y ont un inverse pour la multiplication (c’est le cas des nombres rationnels, par exemple, mais pas des entiers relatifs). En d’autres termes, pour tout élément a d’un corps, il existe un élément, généralement noté a-1, tel que a*a-1=1. On voudrait alors montrer qu’un corps est toujours un anneau intègre.
27L’argument tient en deux lignes. Il suffit, en effet, de supposer qu’il existe deux éléments non nuls vérifiant a*b=0. En multipliant cette formule à gauche par a-1, on obtient que :
28a-1*a*b= (a-1*a)*b=1*b=b
29Mais comme on a également, par hypothèse, a*b=0, on a :
30a-1*a*b= a-1*(a*b)= a-1*0=0
31Les deux expressions étant égales, on a donc que b, qu’on avait supposé non nul, est nécessairement égal à 0. Contradiction46.
32On peut très facilement écrire les axiomes caractérisant un anneau et un corps sous une forme purement symbolique à l’aide d’un langage logique bien choisi, comme celui de la logique du premier ordre. De même peut-on aisément écrire la démonstration qui précède sous la forme d’une simple liste de formules dans laquelle, ayant posé b0 en hypothèse, on parvient au fait que b=0. La preuve qui précède se déroulera alors en une liste de formules, dont certaines seront les prémisses du raisonnement, d’autres des hypothèses et les suivantes des transformations opérées en utilisant les axiomes et les règles ordinaires de la logique formelle (modus ponens, substitution, etc.). On peut également se passer de démonstration par l’absurde et procéder de manière analytique en se demandant s’il peut y avoir dans un corps des éléments a, b, tels que a*b = 0. Par le même raisonnement, on aboutira à la condition qu’il faut alors que l’un des deux soit nul (ce qui est une autre caractérisation de l’intégrité : s’il y a des diviseurs de zéro, alors l’un d’entre eux est nécessairement déjà nul). Le point crucial est que dans tous ces cas, les écritures fonctionnent, toutes choses égales par ailleurs, comme les dessins : ce que nous écrivons au départ peut se révéler impossible (b≠0) ou dépendre de conditions de possibilité cachées (a*b = 0). Nous avons néanmoins imaginé ces situations, au double sens où nous en avons fait la fiction et où nous les avons représentées par une certaine image visuelle : ici, une suite de symboles sur la page. Ce sont des écritures « aveugles », dont on a ensuite montré qu’elles pouvaient parfois ne correspondre à aucun concept (lorsqu’elles enfermaient, sous les hypothèses considérées, une impossibilité).
33Un point important à noter dans tout ceci est que les écritures enferment ni plus ni moins de substrat intuitif que les figures géométriques. Nous avons certes utilisé un certain nombre de propriétés qui peuvent être explicitées par des axiomes, mais pas seulement : par exemple, nous avons pu repérer la différence entre la répétition d’une lettre qui vaut pour identité (la répétition de la lettre a) et la répétition d’une lettre qui vaut pour différence (a suivi du symbole -1). Ainsi nous savons détecter que la suite de symboles a* est différente de la suite de symboles a-1, en ce sens que dans un premier cas le symbole a n’est pas affecté par le symbole qui le suit, alors qu’il l’est dans le second. De même savons-nous faire la différence entre la gauche et la droite des symboles et cette intuition nous permet de voir qu’il y a une démonstration « symétrique » en multipliant à droite par b-1. Bref, nous nous sommes plusieurs fois appuyé sur ces aspects qu’un autre mathématicien particulièrement « rigoureux », Nicolas Bourbaki, rêvait de pouvoir reléguer à de simples problèmes « psychologiques ou métaphysiques » :
Nous n’entrerons pas dans la discussion des problèmes psychologiques ou métaphysiques que soulève la validité de l’usage du langage courant en de telles circonstances (par exemple la possibilité de reconnaître qu’une lettre de l’alphabet est « la même » à deux endroits différents d’une page, etc.). Il n’est guère non plus possible d’entreprendre une telle description sans faire usage de la numération ; bien que de bons esprits aient pu sembler embarrassés de ce fait, jusqu’à y voir une pétition de principes, il est clair qu’en l’occurrence les chiffres ne sont utilisés que comme repères (que l’on pourrait d’ailleurs remplacer par d’autres signes tels que les couleurs ou les lettres), et qu’on ne fait aucun raisonnement mathématique lorsqu’on dénombre les signes qui figurent dans une formule explicitée. Nous ne discuterons pas de la possibilité d’enseigner les principes du langage formalisé à des êtres dont le développement intellectuel n’irait pas jusqu’à savoir lire, écrire et compter47.
34Les présupposés intuitifs sur lesquels s’appuient ici l’utilisation des langages dits « formalisés » sont clairs : il faut savoir « lire, écrire et compter » — rien de moins ! À vrai dire, nous pouvons aujourd’hui mesurer plus clairement ce substrat intuitif du fait que nous possédons des machines capables de « lire, écrire et compter » sous certaines conditions. Comme le faisait remarquer le grand géomètre Bill Thurston :
Quand on considère combien est difficile l’écriture d’un programme d’ordinateur simplement approchant les exigences intellectuelles d’un bon papier de mathématiques, et combien plus grands le temps et l’effort qu’il faut y mettre pour le rendre « presque » formellement correct, il est ridicule de prétendre que les mathématiques telles que nous les pratiquons ne sont pas très éloignées de la correction formelle. Les mathématiques telles que nous les pratiquons sont bien plus formellement complètes et précises que les autres sciences, mais elles sont bien moins formellement complètes et précises dans leur contenu que les programmes d’ordinateurs48.
35Le mathématicien Thomas C. Hales, auteur d’une preuve formelle du théorème de Jordan (que nous recroiserons par la suite) raconte d’ailleurs à ce propos l’anecdote suivante : un auteur, intrigué par la déclaration bourbakiste selon laquelle il faudrait des dizaines de milliers de symboles pour produire formellement le nombre ‘1’, voulut montrer qu’ils avaient grandement surestimé le « coût » d’une telle dérivation formelle et entreprit d’en faire un exact dénombrement ; il s’aperçut alors que l’erreur était inverse de ce qu’il croyait et qu’il faudrait plus de quatre billions (quatre mille milliards) de symboles ! La démonstration que Hales élabora représente, quant à elle, 44 000 étapes de preuves et près de 60 000 lignes de code49. On voit que la déclaration de Thurston, qui s’était lui-même grandement intéressé aux preuves formelles, est loin d’être exagérée — et qu’à l’inverse, l’espoir bourbakiste, selon lequel on pourrait appeler mathématique formelleune mathématique dont le « flair » du mathématicien lui ferait sentir qu’elle n’est pas très « éloignée » d’une traduction formelle complète, est loin d’aller de soi.
36Pour compléter et étendre notre répertoire d’exemples, je partirai pour finir d’un exemple bien connu de démonstration par l’absurde, qui aura le double mérite de nous faire voyager à travers plusieurs théories (topologie générale, géométrie analytique, topologie algébrique, théorie des catégories) et de nous conduire comme par la main vers des pratiques plus contemporaines. Ici aussi, la situation est relativement élémentaire, même si le résultat est loin d’être évident à première vue : il s’agit de montrer qu’il ne peut pas y avoir d’application continue du disque dans lui-même qui n’ait pas de point fixe50. Autrement dit, si nous posons une feuille de papier tendue sur un disque et que nous la chiffonnons à l’envi avant de l’aplatir à nouveau, il y a aura toujours un point qui sera resté à l’endroit où il était au-dessus du disque plan initial.
37On procède par l’absurde en supposant que ce n’est pas le cas. Comme il n’y a pas de point fixe, tous les points du disque vont donc être envoyés par une application continue qu’on appellera f, sur un point distinct qu’on notera f(x). L’idée est alors de regarder la droite déterminée par x et f(x) : elle coupe le disque en un point r(x) dont on peut déterminer les coordonnées par une formule analytique (cf. ci-dessous pour ceux que cette formule intéresserait). Comme il s’agit d’une fonction polynomiale, elle détermine du même coup une application continue permettant d’envoyer continûment n’importe quel point de l’intérieur du disque sur son image sur le bord r(x) (les points du bord restant sur le bord) : c’est ce qu’on appelle une rétraction continue du disque sur son bord. Or il n’existe pas de telle application (c’est le résultat a auquel fait référence la preuve ci-dessous et sur lequel je vais revenir par la suite)51.

38Une des beautés de cette construction, quand on s’intéresse au travail de l’imagination, est qu’elle nous fait voyager d’une impossibilité à une autre tout en mobilisant plusieurs registres de ressources expressives (des dessins, des formules analytiques, de l’algèbre). On pourrait d’ailleurs poursuivre le jeu plus avant puisque le théorème du point fixe peut entrer comme ingrédient dans nombre de démonstrations d’autres théorèmes, comme celui de Jordan (qui stipule que si nous traçons un lacet simple dans le plan, il le découpe en deux régions connexes distinctes, dont l’une seulement est bornée, avec pour frontière le lacet tracé). Symétriquement, on pourra donc montrer de nouvelles impossibilités, comme le fait que le tore ne vérifie pas le théorème de Jordan, en montrant que sa cellule principale ne vérifie pas le théorème de Brouwer qui lui-même impliquerait, etc. etc.
39Regardons maintenant comment on établit qu’il n’existe pas de rétraction du disque (souvent noté B2, pour la boule unité en dimension 2) sur le cercle (souvent noté S1, pour la sphère unité en dimension 1). Cette transformation peut être définie, comme toute rétraction, par le fait qu’on peut d’abord injecter le cercle dans le disque (en le déformant continûment si nécessaire pour qu’il coïncide avec son bord), puis ensuite rétracter le disque sur ce même bord de sorte que la composition de ces deux applications soit simplement l’identité du cercle avec lui-même (noté IdS1). C’est ce qu’indique le premier schéma ci-dessous (qu’on appelle un « triangle commutatif » parce que les flèches s’y composent de sorte que r o i = Id)52. On peut faire la théorie générale de ces flèches entre objets entre lesquelles on ne stipule aucune autre contrainte que la possibilité de composition et l’existence d’application Id sur les objets. Ceci constitue une sorte d’algèbre de niveau supérieur où les structures sur lesquelles on travaille sont elles-mêmes constituées d’applications de niveau inférieur. Prise sous sa forme abstraite (c’est-à-dire indépendamment du fait qu’il existe ou non des structures « concrètes » de niveau inférieur correspondantes), elle relève de la « théorie des catégories ». Un des instruments fondamentaux de cette théorie est la possibilité de transporter les compositions et les identités d’une structure à une autre. Ces « applications » de niveau supérieur sont ce qu’on appelle des « foncteurs » et l’on peut alors définir également des structures de niveaux encore supérieurs (et ainsi de suite, à l’infini). Dans le cas qui nous intéresse, il existe un foncteur qui envoie le monde des applications continues sur celui des groupes fondamentaux (notés π1) — un instrument algébrique qui, intuitivement, mesure le nombre de « trous » dans les objets en regardant les rétractions des lacets qu’on peut y tracer. Or on voit tout de suite qu’un disque n’a pas de trou (on dit qu’il est « simplement connexe ») et ceci se manifeste par le fait que son groupe fondamental est trivial (il est réduit à l’élément neutre : tous les lacets se rétracteront en un point sans jamais rencontrer de trou). En revanche, le cercle a un « trou » central, par construction, et les lacets équivalents correspondront alors à des nombres de tours qu’on peut faire autour de ce trou (le groupe considéré est donc isomorphe à l’ensemble des entiers relatifs Z). Or il ne peut y avoir d’injection du groupe trivial (réduit à l’élément neutre) dans Z53. C’est ce que résume le petit schéma ci-dessous54.

40Ces deux diagrammes sont deux exemples très simples de diagrammes impossibles qu’on rencontrera aujourd’hui dans nombre de manuels de mathématiques. Ils posent aux philosophes exactement les mêmes questions que ceux des géomètres anciens. Même si les propriétés qu’ils portent sont très différentes de celles des figures géométriques, on aurait tort de croire qu’ils sont transparents aux concepts (c’est précisément ce que nous venons de montrer : les deux situations tracées sont conceptuellement impossibles). Par ailleurs, comme dans les autres cas rencontrés, la démonstration par l’absurde peut aisément se transformer en analyse d’un problème, ici de savoir si l’on peut rétracter le disque sur la sphère unité. Voyez la figure ci-dessous où le groupe trivial a été noté cette fois 0 et l’identité 155 :

41Il s’agit là, comme l’avait remarqué Leibniz, d’une pratique inventive particulièrement féconde. Dans le cas auquel nous parvenons, on trace donc des diagrammes « aveugles » et on se demande si on peut les compléter (comme l’indiquent les flèches « ? » dans le dernier exemple). Nombre de démonstrations en théorie des catégories reposent sur de telles questions.
42Ces exemples me serviront surtout pour faire sentir qu’il ne semble y avoir aucune raison de penser que le travail de l’imagination a progressivement disparu des mathématiques au fur et à mesure qu’elles se tournaient vers plus d’« abstraction ». C’est tout l’inverse qui est vrai ! Certes, pour chaque régime expressif, on ne fait pas porter les mêmes informations par les représentations et le travail de l’imagination est plus ou moins bien réglé. L’apprentissage consiste précisément pour une grande part à se familiariser avec ces réglages, parfois subtils. Mais le point qui me semble remarquable est que dans tous ces cas, on se retrouve dans une situation qui était celle sur laquelle s’appuyaient Descartes et Leibniz : d’un côté, on cherche à obtenir un contrôle maximal des représentations en se limitant à un certain nombre d’intuitions simples (éventuellement capturables dans des axiomes) ; de l’autre, il y a un aspect exploratoire qui suspend ces contraintes constructives et autorise à utiliser ces représentations même quand elles ne représentent… rien.
43En ce sens, il me semble que la proposition de Leibniz n’a rien perdu de son actualité. Aujourd’hui, comme hier, une « logique de l’imagination » préside à la pratique des mathématiciens et c’est une tâche urgente pour les philosophes de parvenir à en comprendre le fonctionnement.
Bibliographie
Araujo Silva, M. (2008), « L’imagination dans la géométrie de Descartes », dans D. Descotes et M. Serfati (dir.), Mathématiciens français du xviie siècle : Descartes, Fermat, Pascal, Clermont-Ferrand, Presses Universitaires Blaise Pascal, p. 69-128.
Bos, H. (2001), Redefining geometrical exactness: Descartes’ transformation of the early modern concept of construction, New York, Springer.
Bourbaki, N. (1956), Théorie des ensembles, Paris, Hermann.
Couturat, L. (1901), La Logique de Leibniz d’après des documents inédits, Paris, Alcan.
Descartes, R. (1969-1975), Œuvres de Descartes (11 vol.), ed. C. Adam & P. Tannery, Paris, Vrin. Je cite sous la forme AT, suivi du numéro du tome, suivi du numéro de page.
Descartes, R. (1977), Règles utiles et claires pour la direction de l’esprit en la recherche de la vérité, traduction de Jean-Luc Marion, avec des notes mathématiques de Pierre Costabel, La Haye, Martinus Nijhoff.
Dodson, C.T. et Parker, P.E. (1997), A user’s guide to algebraic topology, Dordrecht, Kluwer Academic Publishers.
Hahn, H. (1933), « Die Krise der Anschauung », dans Krise und Neuaufbau in den exakten Wissenschaften, 5 Wiener Vortrage, 1. Zyklus, Leipzig, Wien, p. 41-64.
Hales, T. C. (2007), « The Jordan curve theorem, formally and informally », Amer. Math. Month., vol. 114, p. 882-894.
Hilbert, D. (1899/1903), Grundlagen der Geometrie, 2nd edition, avec 5 suppléments, Leipzig, Teubner.
Husserl, E. (1976), La Crise des sciences européennes et la Phénoménologie transcendantale, Paris, Gallimard, 1976, rééd. 1989, coll. « Tel ».
Husserl, E. (1984), Logique formelle et logique transcendantale, trad. fr. S. Bachelard, Paris, P.U.F.
Jullien, V. (1996), Descartes : La Géométrie de 1637, Paris, PUF.
Leibniz. G.W. (1850-1853), Leibnizens Mathematische Schriften, éd. C. Gerhardt, Halle, rééd. Hildesheim, New-York, Olms, 1962. Cité GM suivi du tome et de la page.
Leibniz. G.W. (1875-1889), Die philosophische Schriften, éd. C. Gerhardt, Halle, rééd. Hildesheim, New-York, Olms, 1978. Cité GP suivi du tome et de la page.
Leibniz, G.W. (1923-…), Sämtliche Schriften und Briefe, herausgegeben von der Berlin-Brandenburgischen Akademie der Wissenschaften und der Akademie der Wissenschaften zu Göttingen. Je cite sous la forme A, suivi du numéro de la série (par exemple VI pour la philosophie), suivi du numéro de volume (par exemple 4 pour la période 1677-1690) et du numéro de page.
Lejeune, S. (2012-2013), Introduction à la théorie des revêtements et applications, cours de M2, Université de Poitiers, disponible à l’adresse : http://nuxeo.edel. univ-poitiers.fr/nuxeo/site/esupversions/ceab57aa-2552-48e3-8357-b5bcbd95564a (page consultée le 24.10.2106).
Mancosu, P. (1999), « Literature Survey: Recent publications in the history and philosophy of mathematics from the Renaissance to Berkeley », Metascience, 8 (1), p. 102-124.
Mancosu, P. Jørgensen, K. and. Pedersen, S.A (2005), ed., Visualization, Explanation and Reasoning Styles in Mathematics, Dordrecht, Springer.
Mancosu, P. (2008), ed., The philosophy of mathematical practice, Oxford, Oxford University Press.
Manders, K. (2008), « The Euclidean diagram » in Mancosu (2008), p. 80-133.
Michel-Pajus, A. et Rabouin, D. (à paraître), « Logica Mathematica: Mathematics as Logic in Leibniz », dans Fichant M., Pisano R, Agamenon O., Bussotti P. (eds), Homage to Gottfried Wilhelm Leibniz as Scientist and Engineer 1646-2016. New Scientific and Epistemological Insights, London, College Publication(à paraître : 2017).
Miller, N. (2001), A diagrammatic formal system for Euclidean geometry, Ph.D. Dissertation, Cornell University.
Miller, N. (2007), Euclid and his twentieth century rivals: Diagrams in the logic of Euclidean geometry, Stanford, Centre for the Study of Language and Information Press.
Mumma, J. (2006), Intuition formalized: Ancient and modern methods of proof in elementary Euclidean geometry, Ph.D. Dissertation, Carnegie Mellon University.
Mumma, J., Avigad, J., and Dean, E. (2009), « A Formal System for Euclid’s Elements », Review of Symbolic Logic, vol. 2, issue 4, p. 700-768.
Mumma, J. (2010), « Proofs, pictures, and Euclid », Synthese, 175(2), p. 255-287.
Netz, R. (1999), The shaping of deduction in Greek mathematics: A study in cognitive history, Cambridge, Cambridge University Press.
Netz, R. (2009), « Imagination and layered ontology in Greek mathematics », Configurations, 17(1), p. 19-50.
Queffélec, H. (2012), Topologie, Paris, Dunod, 4e éd.
Rabouin, D. (à paraître), « Mathematics and Imagination in Early Modern Times: Descartes and Leibniz’ Mathesis Universalis in the Light of Proclus’ Commentary of Euclid’s Elements », dans K. Vermeir (ed.), Knowledge and imagination in early modern philosophy, Springer.
Rabouin, D. (2015a), « The Difficulty of Being Simple. Interactions between Mathematics and Philosophy in Leibniz’s Analysis of Notions », dans D. Rabouin, Norma B. Goethe et Philip Beeley (eds.), G.W. Leibniz, Interrelations between Mathematics and Philosophy, Dordrecht, Springer, Archimedes Series n. 41, 2015, p. 49-72.
Rabouin, D. (2015b), « Proclus’ conception of geometric space and its actuality », in V. De Risi (ed.), Mathematizing Space. The Objects of Geometry from Antiquity to the Early Modern Age, Basel, Birkhäuser, Series: Trends in the History of Science, p. 105-142.
Rabouin, D. (2013), « Sur la mathesis universalis à l’âge classique. Réflexion pour une histoire de la philosophie des mathématiques », dans A.-L. Rey (dir.), Méthode et Histoire. Quelle histoire font les historiens des sciences ?, Paris, Classiques Garnier, p. 273-287.
Rabouin, D. (2010), « Le rôle de Proclus dans les débats sur la ‘mathématique universelle’ à la Renaissance » dans Alain Lernould (éd.), Études sur le Commentaire de Proclus au premier livre des Éléments d’Euclide, Lille, Presses du Septentrion, p. 217-234.
Rabouin, D. (2009), Mathesis universalis. L’idée de « mathématique universelle » d’Aristote à Descartes, Paris, P.U.F., coll. « Épiméthée ».
Rabouin, D. (2006), « Idée, représentation et correspondance mathématique chez Leibniz », dans Kim Ong-Van-Cung (éd.), La voie des idées ? Le statut de la représentation xvii-xixe siècles, Paris, CNRS-éditions, p. 111-124.
Rauzy, J.-B. (1998), ed., G.W. Leibniz, Recherches générales sur l’analyse des notions et des vérités, Paris, PUF.
Richard, P.R. (2004), Raisonnement et stratégie de la preuve dans l’enseignement des mathématiques, Berne, Peter Lang.
Serfati, M. (1993), « Les compas cartésiens », Archives de philosophie, 56, p. 197-230.
Thurston, W. (1994), « On Proof and Progress in Mathematics », Bulletin of the AMS, Volume 30, Number 2, p. 161-177.
Notes
1 J’ai eu l’occasion d’insister sur cet aspect dans plusieurs publications comme Rabouin (2009), Rabouin (2010) et Rabouin (à paraître).
2 Sur cette distorsion historique, je me permets de renvoyer à l’introduction de Rabouin (2009) et Rabouin (2013).
3 Mathesis universalis tradere debet Methodum aliquid exacte determinandi per ea quae sub imaginationem cadunt, sive, ut ita dicam, Logicam imaginationis (Sämtliche Schriften und Briefe, herausgegeben von der deutschen Akademie der Wissenschaften zu Berlin, series VI, tome 4, 1999, p. 513, désormais cité comme A VI, 4, 513). Sauf mention contraire, toutes les traductions sont miennes.
4 GM VII, 205-206. C’est moi qui souligne. On trouve une caractérisation très semblable dans les Elementa nova matheseos universalis (A VI, 4, 514).
5 Voir, par exemple, la liste déclinée dans le De artis combinatoriae usu in scientia generali (A VI, 4, A, 511) : Logica est Scientia generalis. Mathesis est Scientia rerum imaginabilium. Metaphysica est Scientia rerum intellectualium. Moralis est Scientia affectuum.
6 On trouvera également nombre de textes des années 1690 où les mathématiques sont caractérisées comme traitant des imaginabilia, voyez A VI, 6, 495 ; 499 et 521.
7 Correspondance avec Sophie-Charlotte 1702 [GP VI, 501].
8 Ce point n’est pas sans importance par rapport à une tendance actuelle à relier l’imagination à la seule représentation visuelle.
9 Cette théorie est de provenance néoplatonicienne, voyez Rabouin (2009) et Rabouin (2015b). Leibniz la résume par l’affirmation suivante : « Il y a donc trois rangs de notions : les sensibles seulement, qui sont les objets affectés à chaque sens particulier, les sensibles et intelligibles à la fois, qui appartiennent au sens commun, et les intelligibles seulement, qui sont propres à l’entendement. Les premiers et les seconds ensembles sont imaginables, mais les troisièmes sont au-dessus de l’imagination. Les secondes et les troisièmes sont intelligibles et distinctes ; mais les premières sont confuses, quoiqu’elles soient claires et reconnaissables » (GP VI, 502). Insistons sur le fait que la caractérisation de la structure comme « logique » ne renvoie pour Leibniz à aucune réforme des mathématiques existantes. Sur le sens du mot logique utilisé dans ce contexte, voyez Pajus et Rabouin (à paraître).
10 La ligne de progression dans laquelle s’inscrivent les Elementa nova est indiquée dès leur ouverture : Haec Elementa Matheseos universalis, multo plus different a Speciosa hactenus cognita, quam ipsa Speciosa Vietae aut Cartesii differt a Symbolica veterum (A VI, 4, 513). S’il s’agit de dépasser Viète et Descartes, c’est toutefois dans une histoire continue de la « spécieuse », supposée remonter aux Anciens.
11 E. Husserl, Logique formelle et logique transcendantale, § 26, trad. fr.(1984), p. 111.
12 E. Husserl, Krisis, II, chap. 9, f, trad. fr.(1976), p. 52-53.
13 « En somme, Leibniz a eu le mérite d’apercevoir (bien avant les découvertes et les progrès modernes qui ont rendu cette vérité manifeste) qu’il y a une Mathématique universelle dont toutes les sciences mathématiques relèvent pour leurs principes et leurs théorèmes les plus généraux, et que cette Mathématique se confond avec la Logique elle-même, ou du moins en est une partie intégrante. Il n’y a plus seulement entre la Logique et la Mathématique une analogie formelle, mais une identité au moins partielle. C’est que, d’une part, la Mathématique universelle constitue, comme on l’a vu, la science générale des relations (…). D’autre part, la logique formelle s’étend jusqu’à coïncidence avec la Mathématique. En effet, c’est le caractère formel des raisonnements qui garantit la valeur universelle et nécessaire de la déduction » (Couturat, 1901, p. 317-318).
14 Voyez, par exemple, l’article classique de J. Mittelstrass : « The restriction to formal sciences led to the distinction between a (general) programme to construct a universal science (scientia universalis or generalis) and a limited programme to construct a mathesis universalis. The latter was the attempt to represent the structure of formal sciences in terms of dependency relations controllable mechanically or rather within a calculus, and thereby to put the justification of scientific propositions in terms of a scientific language which satisfies the standards of unity and exactness » (Mittelstrass (1979), p. 594).
15 Selon l’expression célèbre de Hans Hahn (1933).
16 Un des avatars récents et malheureux de cette lecture étant l’opposition entre symbolique et diagrammatique, alors que, comme y avait insisté Peirce, les symboles mathématiques sont, d’un point de vue sémiotique, des « diagrammes ».
17 « Sur l’esprit, l’univers et Dieu » (1675) ; A VI, 3, 463 ; tr. fr.in Rauzy (1998), p. 17.
18 Voyez Règles pour la direction de l’esprit XII : « C’est la même et unique force, qui, si elle s’applique avec l’imagination au sens commun, est dite voir, toucher, etc. si c’est à l’imagination seule revêtue de diverses figures, elle est dite se souvenir ; si c’est encore à elle comme forgeant de nouvelles, elle est dite imaginer ou concevoir ; si enfin elle agit seule ; elle est dite entendre (…). C’est pourquoi aussi cette même force est appelée selon ses diverses fonctions ou bien pur entendement, ou bien imagination, ou bien mémoire, ou bien sens » (AT X, 415, 27-416, 8 ; trad. fr. Descartes (1977). C’est moi qui souligne).
19 Le passage canonique à ce sujet se trouve dans le Discours de la méthode : « Pour les considérer mieux en particulier [les rapports et proportions en général], je les devais supposer en des lignes, à cause que je ne trouvais rien de plus simple, ni que je pusse plus distinctement représenter à mon imagination et à mes sens; mais que, pour les retenir, ou les comprendre plusieurs ensemble, il fallait que je les expliquasse par quelques chiffres, les plus courts qu’il serait possible ; et que, par ce moyen, j’emprunterais tout le meilleur de l’analyse géométrique et de l’algèbre, et corrigerais tous les défauts de l’une par l’autre » (AT VI, 20). Ceci correspond très clairement au développement des Regulae (Règle XVI) où Descartes présente l’intervention des écritures comme une manière de contrôler le fonctionnement de la mémoire (AT X, 454-455).
20 Pour une étude plus complète, voyez Araujo Silva (2008).
21 À Élisabeth, 28 juin 1643, AT III, 691-692.
22 « J’observe toujours, en cherchant une question de géométrie, que les lignes, dont je me sers pour la trouver, soient parallèles, ou s’entrecoupent à angles droits, le plus qu’il est possible ; et je ne considère point d’autres théorèmes, sinon que les côtés des triangles semblables ont semblable proportion entr’eux, et que, dans les triangles rectangles, le carré de la base est égal aux deux carrés des côtés » (À Élisabeth, 17 Novembre 1643, AT IV, 38).
23 « Que s’il est question de considérer un pentagone, il est bien vrai que je puis concevoir sa figure, aussi bien que celle d’un chiliogone, sans le secours de l’imagination ; mais je la puis aussi imaginer en appliquant l’attention de mon esprit à chacun de ses cinq côtés, et tout ensemble à l’aire, ou à l’espace qu’ils renferment » (AT IXa, 58).
24 AT III, 691.
25 Je renvoie ici au travail de H. Bos (2001) qui a fortement insisté sur les aspects constructifs et diagrammatiques dans la pratique mathématique de Descartes. Voyez également Jullien (1996), en particulier la section « L’imagination et la géométrie », p. 12-15.
26 AT VI, 369-372.
27 Objets qu’il s’agit d’ailleurs d’imaginer : « Considérant la géométrie comme une science qui enseigne généralement à connaître les mesures de tous les corps; on n’en doit pas plutôt exclure les lignes les plus composées que les plus simples, pourvu qu’on les puisse imaginer être décrites par un mouvement continu, ou par plusieurs qui s’entresuivent et dont les derniers soient entièrement réglés par ceux qui les précédent: car, par ce moyen, onpeut toujours avoir une connaissance exacte de leur mesure » (AT VI, 389-390). Sur les « compas cartésiens », voyez Serfati (1993).
28 Pour une analyse de cet exemple, mis en avant dans l’Accessio ad arithmeticam infinitorum, je me permets de renvoyer à Rabouin (2006) et (2015a).
29 Voyez notamment les Meditationes de cognitione, veritate, et ideis, Acta Eruditorum, Novembre 1684, 537-542 (A VI 4 585-592).
30 Il est d’ailleurs remarquable que ce sens soit mentionné par Descartes au moment d’envisager des solutions aux équations qui ne soient pas « réelles » : « Au reste, tant les vraies racines que les fausses ne sont pas toujours réelles, mais quelquefois seulement imaginaires : c’est-à-dire qu’on peut bien toujours en imaginer autant que j’ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celles qu’on imagine » (AT VI, 453-454).
31 Voyez Nouveaux Essais sur l’entendement humain (III, 3, § 15 ; GP V, 272).
32 Situation qui arrive d’ailleurs à Descartes à l’occasion, voyez, outre la note 27 ci-dessus, le passage suivant de la solution du problème de Pappus « en trois ou quatre lignes » : « Et si, en toutes ces 4 positions, la valeur d’y se trouvait nulle, la question serait impossible au cas proposé. Mais supposons-la ici être possible… » (AT VI, 399).
33 Sur l’opacité de l’imagination, je me permets de renvoyer à Rabouin (2015b).
34 Rabouin (2009) et, pour une synthèse, Rabouin (à paraître).
35 Voyez notamment Mancosu, Jørgensen and Pedersen (2005), ainsi que Mancosu (2008), dans lequel les quatre premiers articles concernent la visualisation (ainsi que le chapitre XIV).
36 P. Mancosu, E. Grosholz, H. Breger, K. Manders, M. Panza, A. Arana. On doit d’ailleurs au premier de ces auteurs un article de synthèse où il avait insisté dès 1999 sur la manière dont la pensée de l’âge classique pouvait renouveler les thèmes de la philosophie des mathématiques, cf. Mancosu (1999).
37 Manders (2008) et Netz (1999).
38 Mumma (2006). Voyez également Mumma, Avigad and Dean (2009) et Mumma (2010). Miller a proposé une formalisation différente dans sa thèse (Miller (2001), qui a donné lieu au livre Miller (2007)). Elle repose cependant sur le même principe d’un couplage entre régimes d’inférence. Miller (2012) critique le système de Mumma, mais cette critique ne semble pas atteindre le système exposé dans Mumma, Avigad et Dean (2009) et il est trop tôt pour savoir si le système de Mumma peut être corrigé pour échapper aux contradictions. Ces formalisations ne sont ici mentionnées que pour indiquer la fécondité actuelle de l’idée d’une « logique de l’imagination » au sens où nous l’entendons dans cet article.
39 Manders (2008), p. 84.
40 Netz (1999), p. 55.
41 Voyez Netz (2009).
42 Je tire cet exemple de Richard (2004), p. 123.
43 Netz (1999), p. 55.
44 Hilbert (1899/1903), p. 10-11.
45 On les supposera ici l’une et l’autre commutatives.
46 On a simplement utilisé, outre l’existence d’un inverse, l’associativité de la multiplication qui est inscrite dans les axiomes d’un anneau, c’est-à-dire qu’on a : (a*b)*c = a*(b*c) et qu’on peut donc écrire sans préciser a*b*c.
47 Bourbaki (1956), E.1.9-10. C’est moi qui souligne.
48 Thurston (1994), p. 9-10.
49 Hales (2007).
50 Ce théorème est dû au mathématicien L.E.J. Brouwer.
51 Source Queffélec (2012), p.140.
52 La composition des fonctions se note g o f, ce qui signifie qu’on accomplit d’abord la fonction f, puis g.
53 Une injection est définie par le fait que deux points de l’ensemble de départ ne peuvent avoir une même image dans l’ensemble d’arrivée.
54 Lejeune (2012-2013), p. 17.
55 Dodson and Parker (1997), p. 45.