Amand Lucas

A Wave-Theoretic Model of Wind-Induced Wheat Field Motion

Résumé

Nous présentons un modèle physique minimal pour décrire le mouvement ondulatoire des champs de blé sous l’influence d’un forçage éolien structuré. Inspirés par un souvenir poétique attribué à Youri Gagarine et inspirés par les peintures de Van Gogh représentant des champs de blé, nous modélisons le déplacement des extrémités des tiges comme un champ scalaire régi par une équation d'onde bidimensionnelle de type Klein-Gordon avec forçage externe. La fonction de forçage est une superposition de modes harmoniques d’ondes induits par le vent. Malgré la simplicité du modèle, les motifs spatiaux simulés présentent une résonance visuelle et structurelle avec la dynamique de champ observée. Nous abordons également des phénomènes d'ondulation analogues dans plusieurs domaines de la physique de la matière condensée.

Abstract

We present a minimal physical model to describe the undulating motion of wheat fields under the influence of structured wind forcing. Inspired by a poetic recollection attributed to Yuri Gagarin and spurred by van Gogh paintings of wheat fields, we model the tip displacement of stalks as a scalar field governed by a two-dimensional wave equation of the Klein-Gordon-type with external forcing. The forcing function is a superposition of wind-induced wave harmonic modes. Despite the simplicity of the model, the simulated spatial patterns exhibit visual and structural resonance with observed field dynamics. We also discuss analogous undulation phenomena in several areas of condensed matter physics.

Inhoudstafel

Introduction

1Here are a few poetic lines, inspired by Yuri Gagarin’s reported impressions upon returning to Earth in April 1961.

2He spoke not of giant wheeling stars,

3nor of Earth’s curved limb,

4but murmured low, as one recalling dream:

5Not fiery flames, nor the black firmament stirred me so,

6but the breath that combs the golden hide of fields—

7where wheat sways, slow and soft,

8the sacred undulation of the Earth’s most humble choir.

9A sacredness born not of creed, but of motion, resonance, and return —

10the wind touching earth, and the Earth responding with a song.

11In addition to the above homage to the poetic soul of a cosmonaut, I wish to draw the reader’s attention to the extraordinary visual interpretations of wheat fields in motion offered by one of history’s greatest painters, Vincent van Gogh. His series of paintings — freely available in the public domain¹ — provides an artistic context that resonates deeply with the present study. These works capture, with remarkable intuition, both the individual stalk movement and collective undulations of wheat under wind — precisely the physical dynamics explored in this paper.

12While there is no definitive public record of Gagarin utterances upon egress, various memoirs and artistic retellings convey his awe not for cosmic spectacles but for the subtle beauty of terrestrial nature — particularly the rippling fields seen during the late phases of the descent.

13Whether the spectacle Gagarin reported were truly wind-driven oscillations studied here or their superposition with the soft topographic undulations of the Kazakhstan green fields (see Fig. 1) is open to interpretation. What matters is that, to the returning space farer, the surface of Earth — not the cosmos — moved him most. The present work explores the wheat oscillations in physical terms: as a coherent mechanical wave field shaped by wind. Motivated by the evocative images of Fig. 1², we explore a simple physical model to reproduce the motion of undulating wheat fields under wind. The phenomenon has not just biological and ecological relevance, but a physical and visual beauty worth modeling.

14

Fig. 1. Two photographs of wheat field undulations simulated in the present paper, and a photograph provided by Prof. Giorgio Benedek, showing in more detail the structure, size and distribution of ripe wheat stalks in a wheat field in Tuscany

15Analogies to dynamical phenomena observed in condensed matter physics further enrich the model. In particular, the waving wheat stalks evoke classical magnons³— collective modes of precession in spin lattices — or flexural phonons in graphene sheets^4,5, which also involve perpendicular displacements in 2-D fields with coupling and restoring forces. These parallels not only support the model's realism but suggest it may be extended or abstracted toward broader field-theoretic systems in nature.

16In addition to these analogies, the wheat field undulations can also be likened to capillary or ripple waves on a water surface⁶: a thin surface sheet lightly disturbed by a breath (or by water-walking insects) where surface tension (replaced in our model by the bending stiffness and interactions of the stalks) governs the undulating motion. Moreover, one may draw parallels with acoustic waves at the surface of solid substrates, considering the field as a compressible medium, where density fluctuations among wheat ears induce lateral pressure variations even without explicit mechanical coupling.

17A remarkably early conceptualization of wave-like motion in wheat fields appears in Leonardo da Vinci’s Codex Leicester (c. 1508), where he draws an analogy between ripples in water and wind-blown grain fields. Observing that wave patterns do not carry water forward but rather induce a local, oscillatory disturbance, Leonardo wrote:

18“They also noticed that the waves of the sea, or those produced by a stone thrown into a pond, do not move the water forward, but cause a temporary ripple that then returns; they also compared them to the undulations of the wind in a field of grain.”

19(«Notavano anche che le onde del mare, o quelle che produce una pietra gettata in uno stagno, non spostano l’acqua in avanti, ma causano una temporanea increspatura che poi ritorna indietro; le paragonavano anche alle ondulazioni del vento in un campo di grano.»)

20This early analogy anticipates the principle behind modern wave theory: that the medium (water or wheat) undergoes oscillations without net displacement, in striking agreement with the harmonic model developed here. See also⁷ for information on the Codex Leicester.

Model Formulation

21We consider a wheat field as a sheet of vertical stalks; each stalk is modeled as an inverted pendulum of length L ~ 1 m with a tip mass m. The stalk resists its angular deflection from the vertical by a linear restoring torque characterized by a bending stiffness κ. The field is subjected to a force field f(x,y,t) exerted by the wind.

22Using Newton’s law we get an equation

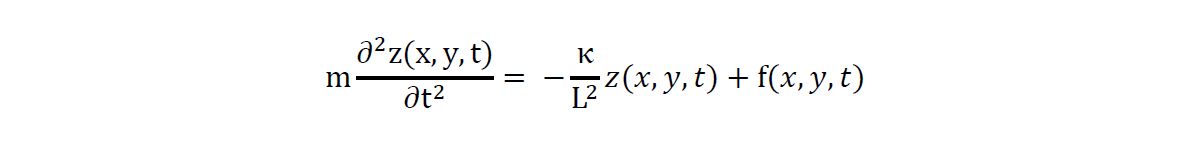
23for the vertical component z of pendulum-like motion of each stalk.

24To allow waves to form (rather than incoherent wagging of the stalks), let’s introduce a weak nearest-neighbor coupling term. This gives us a Laplacian term ∇²z with a small wave speed coefficient v² (discussed below). The final Partial Differential Equation (PDE) for z(x,y,t) is then

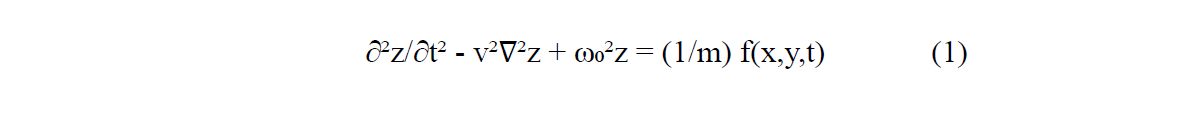
25where ω₀² = κ / (m L²) is the natural frequency squared of an individual stalk and v is the wave velocity of the coherent spread of motion through the field.

Parameters

26To place the model on biological footing, we estimate the bending stiffness κ of wheat stalks based on mechanical properties of hollow, cylindrical plant tissues. We use the relation κ=EI, where E is the Young modulus and I is the second moment of area of a hollow cylinder,

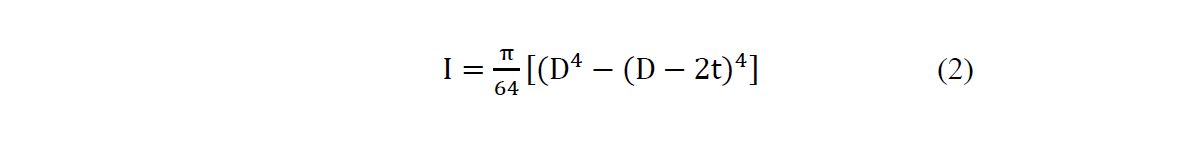
27which is a standard result from beam theory in mechanical engineering and used in Niklas⁸. We estimate a stalk outer diameter D ≈ 5 mm and wall thickness t ≈ 0.5 mm. E can range from 1 to 10 GPa reflecting the variable stiffness along the length of the stalk. Literature estimates of bending stiffness in cereal stems support this range9. The stalk is composed of cellulose, hemicellulose (molecular glue made of polysaccharide), and lignin (a biopolymer that stiffens plant cell walls). We adopt the representative value E ∼ 5 GPa consistent with dry, cellulose-based plant tissue. One obtains κ = EI ∼ 2×10⁻³Nm. This value gives a natural frequency ω₀ ∼ 2 rad/s (for L = 1 m stalk) used in our simulation (see below). Note that κ may also vary under different conditions (e.g., green vs. dry stalks, etc.).

28Although each stalk responds individually to wind, neighboring wheat plants interact in several ways. In dense fields, a dynamical interaction can arise through aerodynamic coupling, where the airflow deflected by one moving stalk alters the wind field felt by its neighbors. In addition, inter stalk interaction may take place via their extended root system in the soil; Moreover, mechanical contact between ears and stalks also transmit forces laterally, particularly under high wind. These effects justify the presence of nearest-neighbor coupling in our model, explaining how coherent wave motion propagates across the field. An average velocity v will result in a collective wavelength-dependent wave frequency ω(k), despite the autonomy of individual stalks. In view of the predominant effect of the wind forcing, the damping associated with the nearest-neighbor interaction is ignored.

Klein Gordon Equation (KGE)

29The PDE (1) is a Klein-Gordon-type wave equation (KGE). Before quantum mechanics, such equations did not have a specific name, but its form was already well known in classical physics, particularly as a wave equation with a mass-like term. Such an equation arises as a universal description of wave-like dynamics in many systems with local inertia, lateral coupling, and restoring forces — of which the present wheat field is just one vivid and illustrative instance. In particular, a KGE can describe elastic membranes and plates (transverse displacements), coupled pendula chains, acoustic fields at the surface of 3-D media with restoring forces, lattice models with nearest-neighbor coupling, etc.

30The reader may be interested in how the name KGE arose historically in quantum theory. Schrödinger’s equation is not consistent with relativity because the equation does not treat time on the same footing as space coordinates. Klein¹⁰ and Gordon¹¹ original works were early attempts to correct that by formulating a relativistic invariant quantum equation. In relativity, energy E and momentum p are related by:

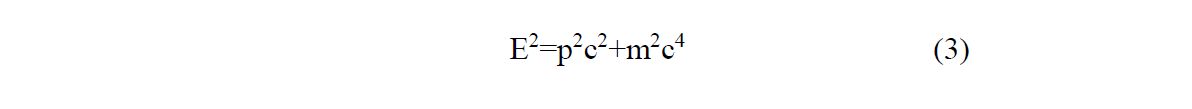
31where c is here the velocity of light.

32In quantum mechanics, energy and momentum are operators given by (in units ℏ = 1, c = 1): E → i/∂t, and p = −i∇. Substituting these into the energy-momentum relation (3), gives the KGE for the free-field scalar wave function ψ

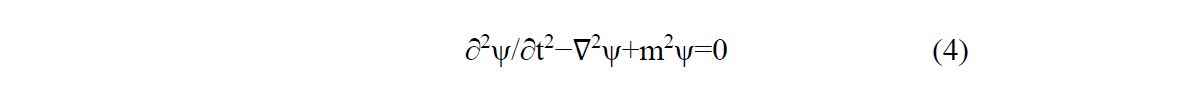
33which has an identical form to (1) for f = 0. The quantum mechanical KGE had two main drawbacks: i) for the electron, it did not include spin and ii) the solutions in a central field did not agree with the observed spectrum of the hydrogen atom. It was Dirac, in 1928, who famously discovered the correct quantum equation for the electron. Dirac’s equation, besides several other virtues, gave the electron a spin (showing its relativistic origin) and produced solutions in a Coulomb in near-perfect agreement with the existing experiments. Further experiments, performed later, led to the discovery of the Lamb shift and the hyperfine structures of the hydrogen spectrum (caused by the coupling between the electron and the proton spins) which launched quantum electrodynamics (QED). In quantum field theory the KGE was reinstated to represent -mesons¹² of zero spin and charge 0 or 1, after the discovery of these particles.

Free Field Dynamics and Analogies

34Consider first the homogeneous KGE for a free wheat field:

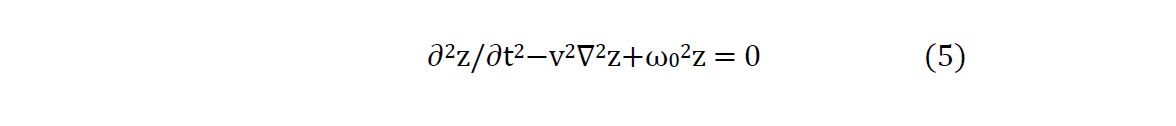
35Plane waves

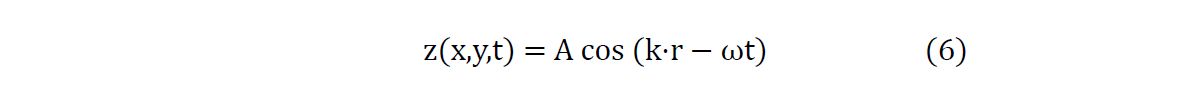
36are solutions provided a parabolic dispersion relation is satisfied:

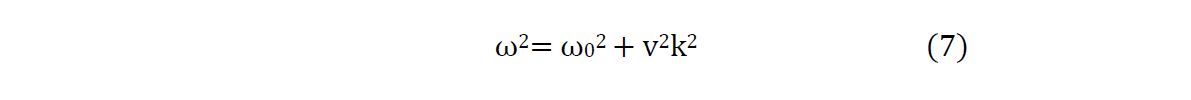
37or, for small k,

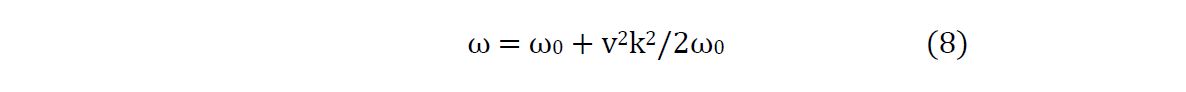
38This behavior is entirely similar to that of classical spin waves (whose quanta are called magnons) in ferromagnetic materials. In the long-wavelength limit, the magnon dispersion relation is also quadratic in k:

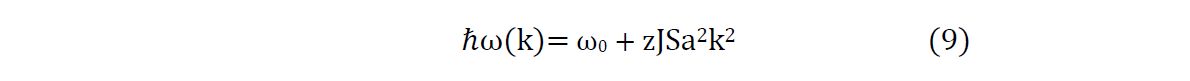
39where S is the spin, a is the lattice constant, J is the exchange interaction constant in Heisenberg’s model of ferromagnetism¹³., z is the number of nearest neighbors. The value of the frequency gap ω₀ = H_eff involves the spin gyromagnetic ratio and the local magnetic field H_eff (external + anisotropic).

40It is interesting to note that the magnons dispersion relation in antiferromagnetic (AFM) materials, by contract to the ferromagnetic (FM) case of Eq. (9), has a magnon branch linear at small k: ω = ω₀ + bk, where b JSais yet another constant. The presence of two coupled sublattices of counter-oriented spins in AFM is what gives the linear, acoustic-like magnon branch. In addition, AFM materials have a magnon “optical” branch as well, displaying a quadratic dispersion above a gap, similar to (9). In FM materials the absence of counterbalance between opposite spins leads to a single, quadratic, “free-particle-like” dispersion.

41Another analogy is provided by the transverse (flexural) phonons in an overlayer graphene sheet14 (a graphite monolayer over a substrate), share this quadratic form in the small k limit:

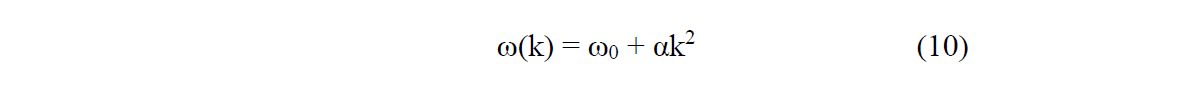
42where ω₀ represents the binding rigidity to the substrate and where the coefficient α is related to the bending resistance and mass density of the overlayer sheet.

43In all three cases (8)-(10), the quadratic form is in fact imposed by reflection and rotational symmetry for out-of-plane motions in a free-standing 2-D sheet.

44This quadratic behavior contrasts with the linear dispersion

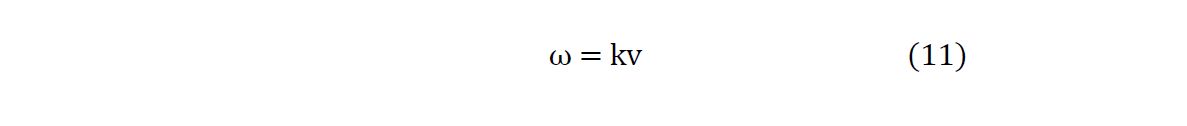
45of acoustic phonons of any polarization in elastic materials, where v is the mode velocity. These materials also possess “optical” branches of quadratic dispersion for small k, as well as families of localized phonon modes¹⁵ associated with the symmetry breaking at surfaces, edges and corners.

Wind Forcing Function

46We model the wind forcing as a superposition of a few traveling wave modes:

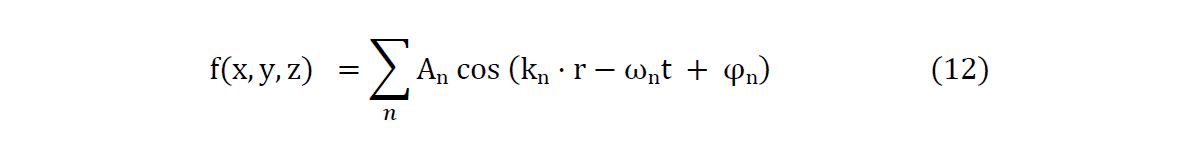
47where kₙ = (kₓₙ, k_yₙ) are 2-D wave vectors, Aₙ amplitudes, ωₙ frequencies, and φₙ phases. This non-random forcing is meant to mimic the effect of coherent gusts and atmospheric travelling waves sweeping over the field. All parameters defining the wind forcing used here (see appendix) are randomized at the beginning of the simulation but remain fixed throughout. The time dependence enters only through oscillatory terms ω_nt producing a structured and coherent field evolution rather than turbulent or stochastic motion.

48The forcing function f(x,y,t), while harmonic in time and space, does not itself satisfy the KGE. Rather, it acts as a structured external driver. The field z(x,y,t) responds according to its own modal structure — governed by the above dispersion relation — and resonates selectively when the driving overlaps with natural modes. This driving term leads to the structured wavefield seen in the simulations below, despite the non-resonant origin of the input.

Simulation

49We use the realistic parameters:

50• Tip mass: m = 0.005 kg
• Natural frequency: ω₀ = 2 rad/s
• 2-D domain: x, y ∈ [0, 50] m

51For simplicity, we have not included a damping term like ∂z/∂t in the KGE (1) whose effect would be to dissipate any intrinsic field motion, independent of the force-field. In the simulation, we focus on the late-time behavior of the system, where transient waves arising from initial conditions have decayed or dispersed. The steady-state displacement is then approximated as:

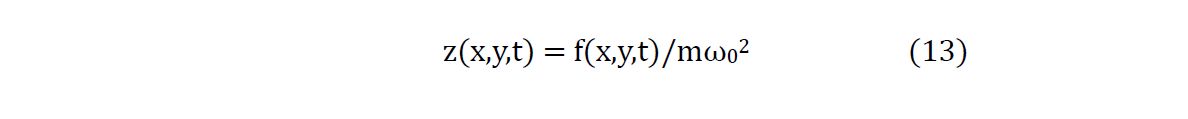
52

53The resulting pattern represents the particular solution to the inhomogeneous KGE under structured wind forcing — capturing the field’s dynamic response as it synchronizes with the driving modes. For intuition and visualization, we consider the quasi-static approximation z ≈ f/mω₀² valid at long time, when the field response is dominated by the local restoring force and the inertial and spatial coupling terms have become small. The quasi-static approximation captures the large-scale undulation pattern shaped by the wind field. A more complete treatment would involve time-resolved integration of the field’s wave response.

54Pattern snapshots of the field are shown in Fig. 2 in two states of maturation.

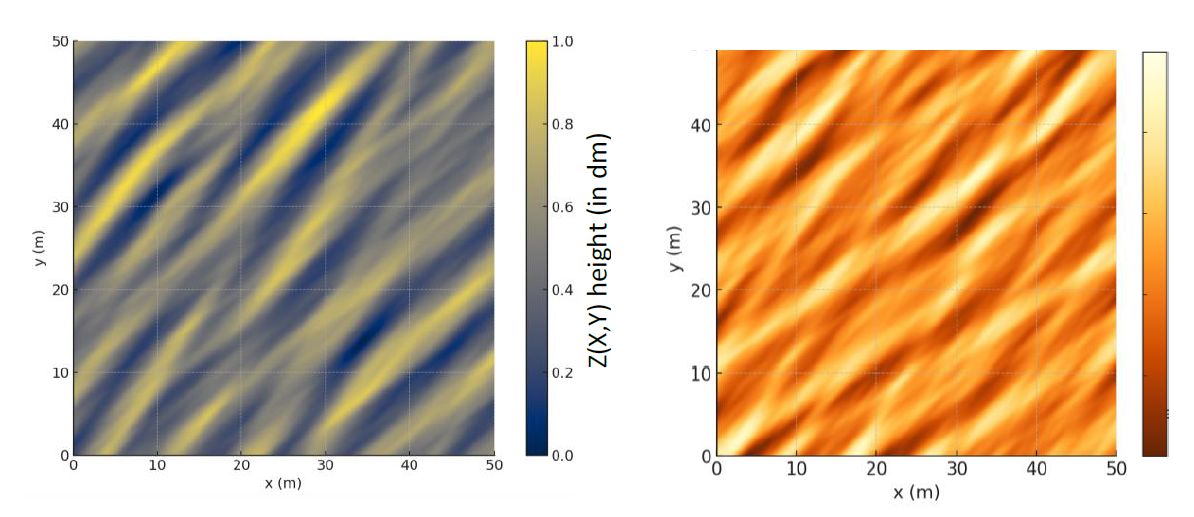
Fig.2. Simulated wheat field undulations (left: immature; right: mature). The color scales are the same (both from 0 to 1 dm).

Discussion

55The model presented here offers a simple yet powerful lens into natural wave phenomena in plant fields. Inspired by Gagarin’s as well as Van Gogh’s poetic visions, it bridges mechanics, aesthetics, and nature. The visual realism of the simulated undulations demonstrates the expressiveness of basic physical models when thoughtfully parameterized.

56By tuning the wavevector distribution in the forcing field, we can simulate different scales of atmospheric modulation. Lower k components lead to slower, broader undulations — resembling the kilometer-scale patterns seen from above — while higher k components produce more rapidly varying wavefronts on the scale of individual crop densities.

57Although analogies to phonons, magnons, or ripplons help conceptually frame the wheat field as a wave-supporting medium, any notion of discrete excitations—agrons, say—remains poetic. The energy scale of a single field mode, ℏω₀∼10⁻³⁴ J is vanishingly small — well below thermal or vibrational noise. No physical experiment could detect such quanta. In a similar way, a bended arc may be conceived as a macroscopic “mechanical laser,” but the elementary excitations are so tiny that one can hardly speak of arcons. These terms are used here by analogy, to emphasize the layered structure of response: from individual motion to collective waves.

Appendix

Parameter	Symbol	Value / Range	Notes
Number of modes	N	50	Total superposed wave components
Domain size	Lx×Ly	50 m × 50 m	Horizontal simulation area
Grid resolution	Nx×Ny	300 × 300	For spatial fidelity
Wavevector magnitude	kn	[0.63, 6.28] m⁻¹	Corresponds to wavelengths of 1–10 m
Wavevector direction range	θn	[120°, 150°] or [2π/3,5π/6]	Reflecting wind from SE toward NW
Amplitude scaling	An	∼ kn−2	Inverse-square decay with wavevector magnitude
Phase offset	ϕn	Uniform in [0, 2π]	Random for visual variety

Acknowledgements

58I am grateful to Prof. Giorgio Benedek, Foreign Member of the Belgian Academy, for drawing my attention to Leonardo da Vinci’s analysis of waves on water surface and on wheat fields

59The author acknowledges the help of AI’s which significantly accelerated the completion of this work.

Voetnoten

Om dit artikel te citeren:

Over : Amand Lucas