- Accueil
- Volume 90 - Année 2021
- Articles
- What apsidal motion reveals about the interior of massive binary stars
Visualisation(s): 2700 (97 ULiège)
Téléchargement(s): 139 (0 ULiège)
What apsidal motion reveals about the interior of massive binary stars

Document(s) associé(s)
Version PDF originaleAbstract
Apart from asteroseismology, the most efficient observational technique allowing to probe the internal structure of a star is the determination of the apsidal motion in close eccentric binary systems. This secular precession of the major axis of the binary orbit depends on the tidal interactions between the two stars. The rate of this motion is directly related to the internal structure of the stars, in particular their inner density profile. Based on radial velocity and light curve measurements made over a long timescale, the rate of apsidal motion can be constrained, together with the fundamental parameters of the stars. Comparing the observationally determined parameters to theoretical models of stellar structure and evolution then constrains the internal structure of the stars. This powerful technique has been known for years, but has been seldom applied - we are reviewing its interest and reveal recent results.
Table des matières
Cet article a reçu un des deux Prix Annuels 2021 de la Société Royale des Sciences de Liège. This paper was awarded one of the two Annual Prizes 2021 of the Société Royale des Sciences de Liège.
received 12 November 2020, accepted 16 December 2020
Note of the Editor: We apologize to our readers that there may be some minor discrepancies in the appearance of mathematical symbols when comparing equations and the main text in the html version. In particular, the dot in ω̇ should appear on top of the ω letter in the main text. Please refer to the pdf version if in doubt.
1. Introduction
1Massive stars, although less abundant in the Universe than solar type stars, play a key role in the Universe, notably in the enrichment of the galaxies through their radiation-driven stellar winds. This is why stars more massive than about ten solar masses can be truly named "Cosmic Engines" [1]. Main sources of UV radiation, but also important sources of chemical and mechanical feedback into the interstellar medium, these hot and luminous objects have a relatively short lifetime compared to solar type stars, of the order of ten millions years. At the end of their life, massive stars vehemently expel their external layers into the surrounding medium in a spectacular core-collapse supernova, while the core follows its contraction until becoming either a neutron star or, for the more massive ones, a black hole.
2Massive stars are seldom isolated from each other, but mostly are – or have been – part of a binary or higher multiplicity system [2]. According to current estimates, at least 70% of the massive stars located in our Galaxy belong to a binary system [3]. Being bound to another star by gravitational attraction may change the evolution of the star. Whilst an isolated massive star sees its evolution completely determined by three properties which are its initial mass, its rotational rate and its mass-loss rate [4, 5], the evolution of a binary star is much more complex and depends not only on the intrinsic properties of the considered star, but also on the properties of the whole binary system, including the properties of the companion and of the orbit itself [6]. The ways stars belonging to a binary system might interact are as diverse as the number of binary systems, and so are the evolutionary paths of massive binary stars ([7, 8]). We here just mention briefly a few. Some of the binary systems experience Roche lobe overflow episodes in the more advanced stages of their evolution, during which some matter leaves the gravitational attraction from one star (the mass loser), and falls onto the companion (the mass gainer) or is ejected from the system. At some point, the stars might expand and/or the orbit might shrink, leading to the merger of the stars.
3Roche lobe overflow and mergers are certainly the most extreme cases of interactions in massive binary stars. However, from the earliest phases of their evolution, stars orbiting one another on a close orbit exert a gravitational attraction on their companion which is strong enough to induce a dynamical deformation of their companion’s stellar surface. This interaction is called tidal interaction, and is responsible for angular momentum exchanges between the two components. It is similar to the tides exerted by the Moon on the Earth (and by the Earth on the Moon). In response to this gravitational attraction, the stellar surface and gravitational field adopt non-spherical shapes. These interactions are dynamical in the sense that the non-spherical shapes of the stars are not static in time: the bulges move on the stellar surface as the stars rotate around each other [9]. The non-spherical shape and gravitational field of the stars in turn induce a secular change of the orbital parameters [10], that is to say, the variations do not happen on the timescale of the orbital period but on much longer timescales. The most prominent manifestation of this effect is the slow precession of the argument of periastron of the binary, also known as apsidal motion.
4The rate of apsidal motion is directly related to the internal structure of the binary stars (see for instance [11, 12]). Hence, the accurate measure of this movement yields information about the internal structure of the stars and their evolutionary state. This possibility is extremely valuable for massive stars, as such information is rather scarce [13]. The most valuable binary systems for such a study are the special cases where the binary is a twin system, meaning that the two stars making up the system have essentially the same fundamental parameters such as the mass, radius, effective temperature, and luminosity. Indeed, these systems offer a very unique opportunity to obtain stringent constraints on the internal mass distribution inside the stars.
2. Geometrical representations of apsidal motion
5To zeroth order, the stars of a binary system orbit each other following ellipses whose focus is their common centre of mass. In general, the more massive star is called the primary star while the less massive companion is called the secondary star: we adopt this convention throughout this paper. Figure 1 illustrates the motion of the primary (P) and secondary (S) stars around their common centre of mass (CM). Both ellipses have the same eccentricity e, whilst the semi-major axis of the orbits of the primary and secondary stars are respectively ɑP and ɑS. As the secondary star is less massive than the primary star, ɑS is larger than ɑP. During one orbit, the stars alternatively move closer to and away from each other. This is illustrated in Fig. 1, where the position of the primary and secondary stars, respectively Pj and Sj, is shown at time tj (j = 1, 2, 3). The point of closest approach (when j = 1) is called periastron whilst the point located on the opposite, the point of largest separation (when j = 3), is called apastron. Those two points are called apsides.
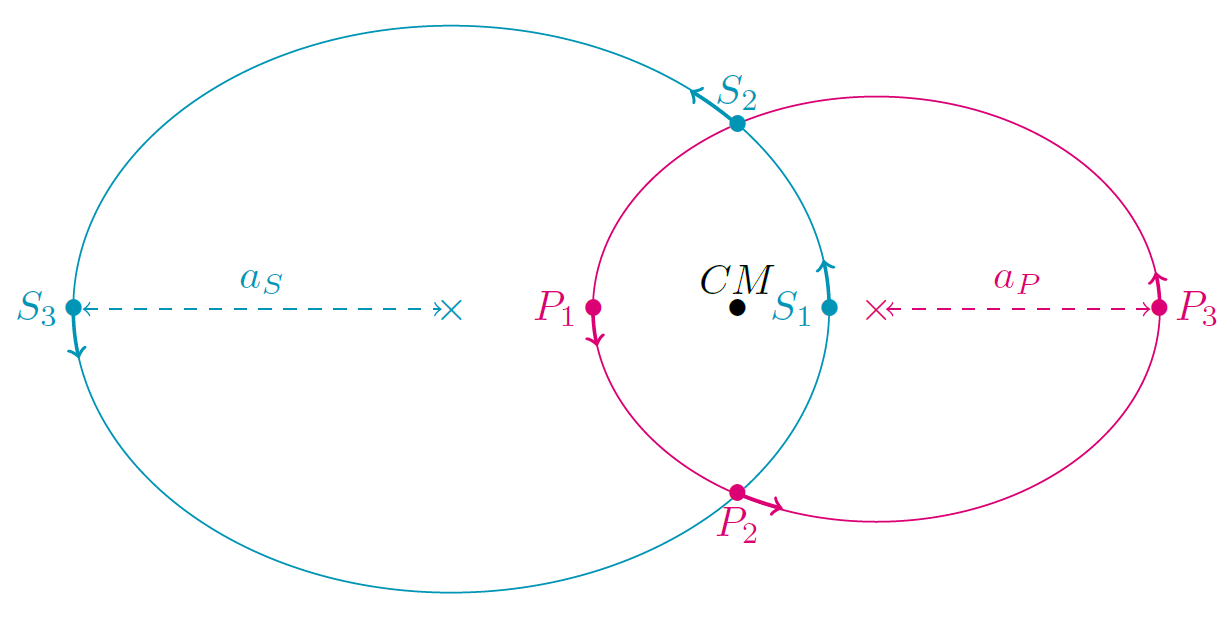
Figure 1.
Orbits of binary stars around their common centre of mass. See text for details.
6In practice, it is easier to visualise the motion of a binary system as the motion of the secondary star around the primary star: the primary star is assumed to be fixed and the secondary star moves on an orbit of eccentricity e and semi-major axis ɑ = ɑP + ɑS whose focus is the primary star. Observed from Earth, the plane of such an orbit is inclined by the inclination angle i with respect to the plane of the sky, as schematically depicted in Fig. 2. The orbital plane and the plane of the sky intersect along the line of nodes (in green in Fig. 2), one of its extremities, denoted by Ω0, is the ascending node. The angle between the reference direction and the direction of Ω0, denoted by Ω and measured in the reference plane, is the longitude of the ascending node. The argument of periastron, denoted by ω, is the angle measured in the orbital plane between the line of nodes and the direction of periastron. The true anomaly ν is the angle, measured in the orbital plane, between the direction of periastron and the position of the secondary star.
7The apsidal motion is the slow precession with time of the line of apsides, that is to say, the change of ω. The rate of apsidal motion is denoted by ω̇, where the dot symbolises the total time derivative of ω, that is to say, dω/dt. Geometrically, it means that the binary orbit precesses with time in the orbital plane.
8Historically, the discovery of apsidal motion dates back to the 2nd century B.C., when the Greek astronomer Hipparchus highlighted some anomalies in the lunar orbital movement around the Earth [14]. With the advent of the Newtonian mechanics, the apsidal motion observed in several planets of our Solar System were explained by the gravitational attraction exerted mainly by the Sun and, to a lesser extent, the other solar bodies. However, one case remained unsolved during about 60 years: the perihelion precession of Mercury, the closest planet to the Sun. The problem was pointed out in 1859 by the French astronomer Urbain le Verrier: whilst about 93% of the apsidal motion of Mercury could be attributed to the Newtonian effects, the remaining 7% were still unexplained. Several solutions were proposed in the course of the following years, all unsuccessful except one: Albert Einstein’s theory of General Relativity. The previously unexplained part of Mercury’s perihelion precession is there explained by a drag of space-time by the Sun. It was probably the result that contributed the most to the acceptance of General Relativity by the scientific community in the early years.
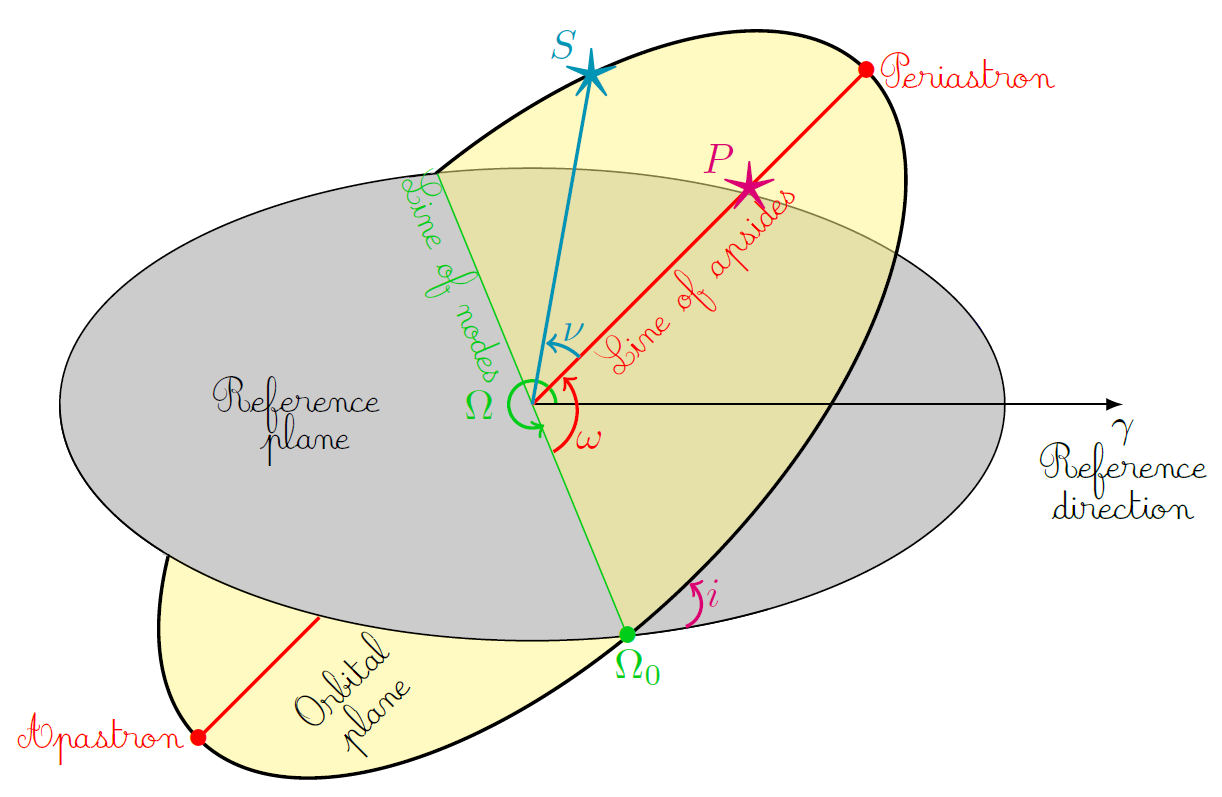
Figure 2.
Definition of the orbital elements. The plane of the sky (the reference plane) is depicted in gray and the γ-axis denotes the reference direction in this plane. The orbital plane is depicted in yellow. In the orbital plane, the primary and secondary stars are schematised by the pink and cyan stars, respectively. The line of apsides, which connects the periastron and apastron, is depicted in red. See text for details.
3. How to determine the apsidal motion rate based on observations
9The apsidal motion rate in a binary system can theoretically be measured in two different ways, either through the analysis of the light curve or through the analysis of the radial velocity curve. The method one would use mainly depends on the considered system and its properties. We now review the two methods that allow to determine the apsidal motion rate in a binary system. In both cases, the feasibility strongly depends on the time-span of the observational data. Indeed, the apsidal motion being slow, the availability of observations over a sufficient time span is a necessary condition to hope to determine the rate of this movement accurately. The need for a huge set of observational data spanning several years or even decades is a very restrictive condition in practice and explains why the study of apsidal motion in binary systems is quite a recent (mid of the 20th century) subject in astronomy.
3.1. In an eclipsing binary.
10In order to detect and constrain the apsidal motion rate based on a photometric analysis, the inclination of the system has to be high enough that eclipses of the two stars are observed during an orbital cycle. Usually, an inclination close to 90° is required to observe eclipses in the light curves of a binary. Other factors, such as the eccentricity of the orbit, the effective temperatures of the stars, and their Roche lobe filling factors, are known to influence the shape of the light curve but of course, in this paper, we focus on one parameter: the argument of periastron. Its strong impact is illustrated in Fig. 3: nine light curves having nine different values of ω ranging from 0° to 160°, all other parameters being identical, are presented. By convention, we have assumed that the primary eclipse always occurs at phase 0 (and is repeated at phase 1), which explains why only the phase of the secondary eclipse changes with ω. Hence, we can easily highlight the impact of the ω-value on the secondary eclipse (and to a lesser extent on the primary eclipse, although it is less affected for this range of ω-values because primary eclipse happens closer to periastron passage while secondary eclipse happens closer to apastron passage). The special case we present in Fig. 3 corresponds to two stars having exactly the same effective temperature. Hence, the unequal depths of the minima observed for all ω-values (except at ω = 0°) do not arise from a difference in surface brightness of the two stars, but are entirely attributable to the value of the argument of periastron. Indeed, in an eccentric binary seen under an inclination of less than 90°, the depth of an eclipse depends on the orbital separation between the two stars at the time of the conjunctions: the closer the eclipse occurs to periastron, the deeper it is. The orbital separation at conjunction phase obviously depends on the orientation of the ellipse with respect to our line of sight, that is to say on the argument of periastron ω at the epoch of the observations. Likewise, the photometric variations outside of the eclipses stem from the elongated shape of the stars and their changing aspect angle with respect to our line of sight as the stars revolve around their common centre of mass. Maximum brightness of these ellipsoidal variations (i.e. the bumps) occurs at quadrature phases, and the duration that the stars spend around quadrature depends through Kepler’s second law on the orbital separation: the closer the quadrature occurs to apastron, the flatter the bump. Hence, the shape of the bumps changes with ω. Finally, in Fig. 3, the light curves are normalised at phase 0.25, which explains the changing height of the bumps.
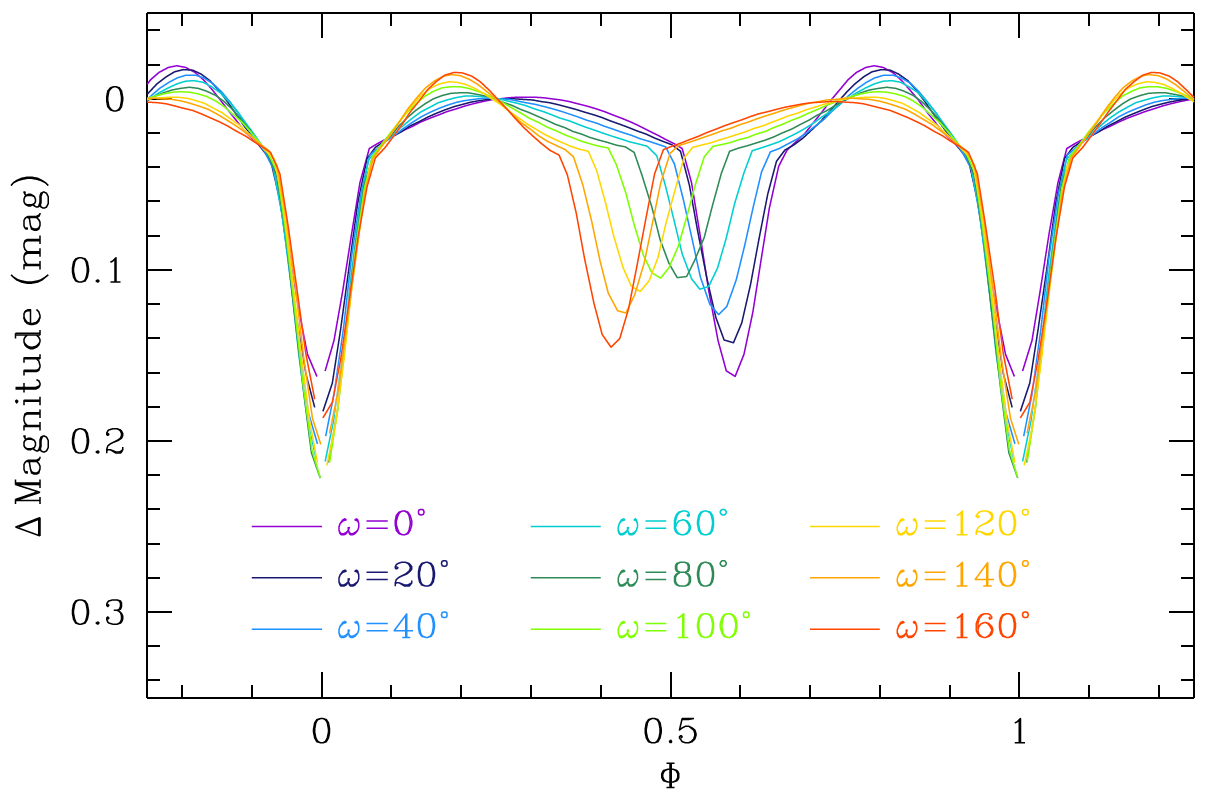
Figure 3.
Set of theoretical light curves for different values of the argument of periastron ω, all other parameters being identical (an eccentricity of 0.134, an inclination of 68.6°, and Roche lobe filling factors of 0.86 for both stars).
11From this simple example, it is clear that, if a binary system experiences apsidal motion, a set of light curves obtained at different epochs can in principle be used to infer the apsidal motion rate of the system. Such an analysis can be done in two ways. The first method is to analyse data obtained at different epochs separately and to infer a value of ω for each epoch, keeping all other parameters identical.
12This method has been applied using the Nightfall code (a freely available code developed by R. Wichmann, M. Kuster, and P. Risse [15]) in [16]. The second method is to simultaneously fit all the observational data with a code allowing for the argument of periastron to vary by a linear rate of change in time, thus directly handling apsidal motion rate. Such an analysis has been applied using the PHOEBE code (an open-source project, see [17, 18]) in [16, 19].
3.2. In a spectroscopic binary.
13If the inclination of the orbital plane with respect to the plane of the sky is non-zero, then the stars of a binary system alternatively move towards and away from us along our line-of-sight during one orbital cycle, that is to say, their velocity along the line-of-sight (called radial velocity) changes with phase. When the star moves towards us (resp. away from us), its radial velocity is by convention negative (resp. positive). Of course, when one star is moving towards us, the other one is moving away from us, and conversely. If the orbit experiences apsidal motion, the radial velocity curve of the binary star changes with time.
14In practice, the radial velocities of the stars are derived from the Doppler effect on the spectra of the stars. Exactly like the Doppler effect acting on the frequency of an ambulance’s siren, frequency that increases when the ambulance rides towards us and decreases when it rides away from us, the movement of the star along the line-of-sight alternatively blue- and red-shifts its spectral lines as the star moves towards and away from us. Mathematically, it can be written
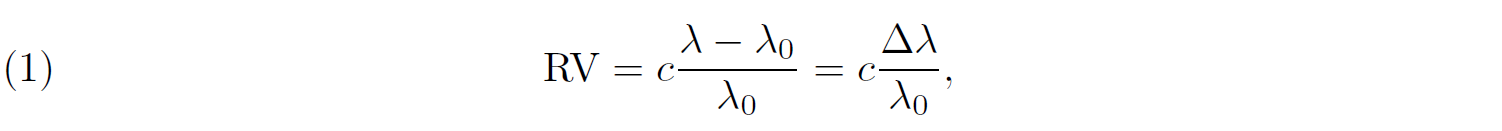
15where c is the speed of light, RV is the radial velocity of the star, and λ and λ0 are respectively the observed and rest wavelength of the considered line. Hence, if we can measure the blue- and red-shifts of the spectral lines during the orbital cycle, they can be used to infer the radial velocity curve.
16An example of such phenomenon is depicted in Fig. 4, where spectra of the massive binary HD 152248 are presented for different orbital phases ϕ. At phases ϕ close to 0 and 0.5, the spectral lines of the two stars are superimposed and their wavelengths are close to the rest values. At these phases, the radial velocities are small. At phases close to 0.25 and 0.75, these lines are completely deblended, one line being blue-shifted whilst the other one is red-shifted. At these phases, the radial velocities take their extremum values. Such a binary where both the primary and secondary spectral lines are visible is called a double-line spectroscopic binary (SB2).
17In order to compute the radial velocities at each phase from a set of spectra, the easiest technique is to fit two Gaussians on well deblended lines. This technique suffers from a lack of accuracy because it strongly depends on the position of the centroid of the line, and is not reliable when the lines are not well deblended. A more elaborate technique is the disentangling method [20], which consists in simultaneously reconstructing the individual spectra of the stars while inferring radial velocities of the stars for each observation. This is done in an iterative way and could be applied with success in several cases (see for instance [21, 16], and Fig. 5). The advantage of this method is twofold: the reconstructed spectra can be analysed by means of a model atmosphere code such as CMFGEN [22] or FASTWIND [23, 24, 25] to infer stellar fundamental parameters (notably the effective temperature and the bolometric luminosity of the stars), while the radial velocities are more accurate that the ones obtained with the two-Gaussian fitting.
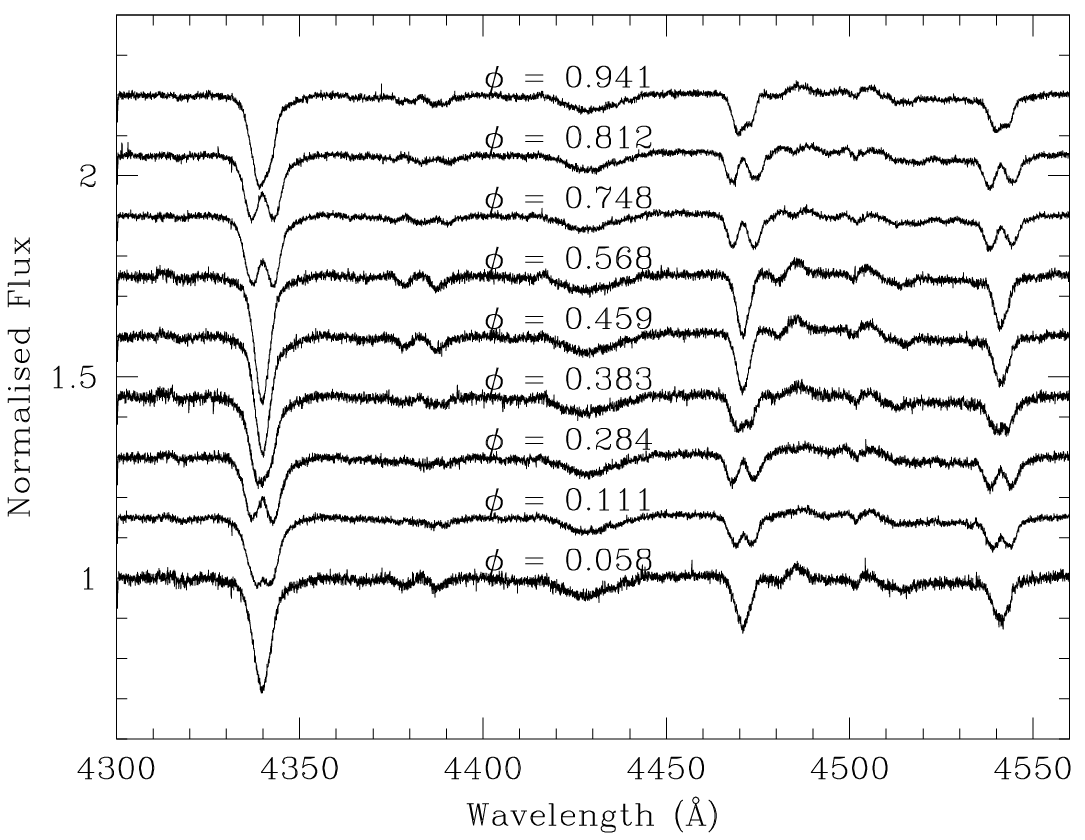
Figure 4.
Phase variations of the lines observed in spectra of the massive binary system HD152248 between 4300 and 4550 Å. Corresponding phases are indicated above each spectrum. The lines of the primary and secondary stars – which have similar depths – are alternatively blue- and red-shifted over the orbital cycle.
18The radial velocities at time t of the primary and secondary stars of a binary system are given by
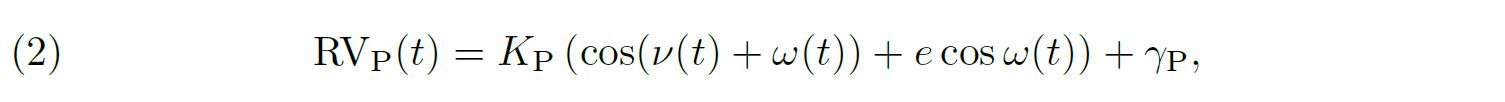
19and
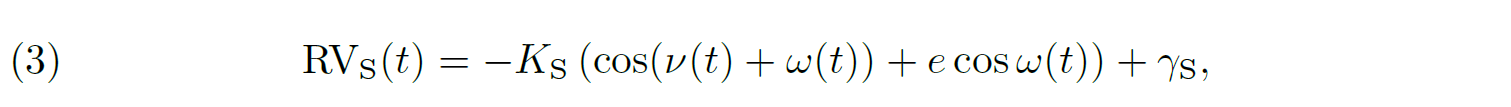
20where KP and KS are the amplitudes of the radial velocity curves, and γP and γS are the apparent systemic velocities. The true anomaly ν is computed from Kepler’s equation with a specific value of the orbital period Porb of the system, the eccentricity e, and the time of periastron passage T0. If the binary orbit experiences apsidal motion at a rate ω̇, the longitude of periastron of the primary star at time t, ω(t), is given by
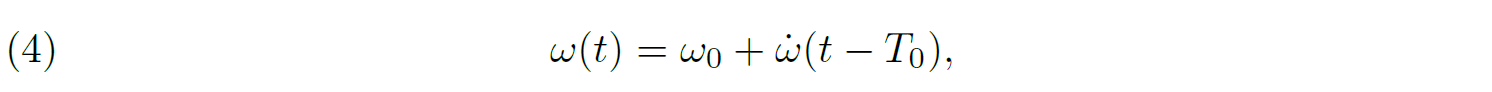
21where ω0 is the argument of periastron at time T0. In practice, the determination of the apsidal motion rate in a binary system then consists in adjusting a set of nine parameters: Porb, e, T0, ω0, ω̇, KP, KS, γP, and γS. As an example, Fig. 6 shows the adjustment of the radial velocity curves of the massive binary HD 152248 for four different epochs, the first and last being separated by 67 years. The change of morphology of the curves due to the apsidal motion is clearly seen.
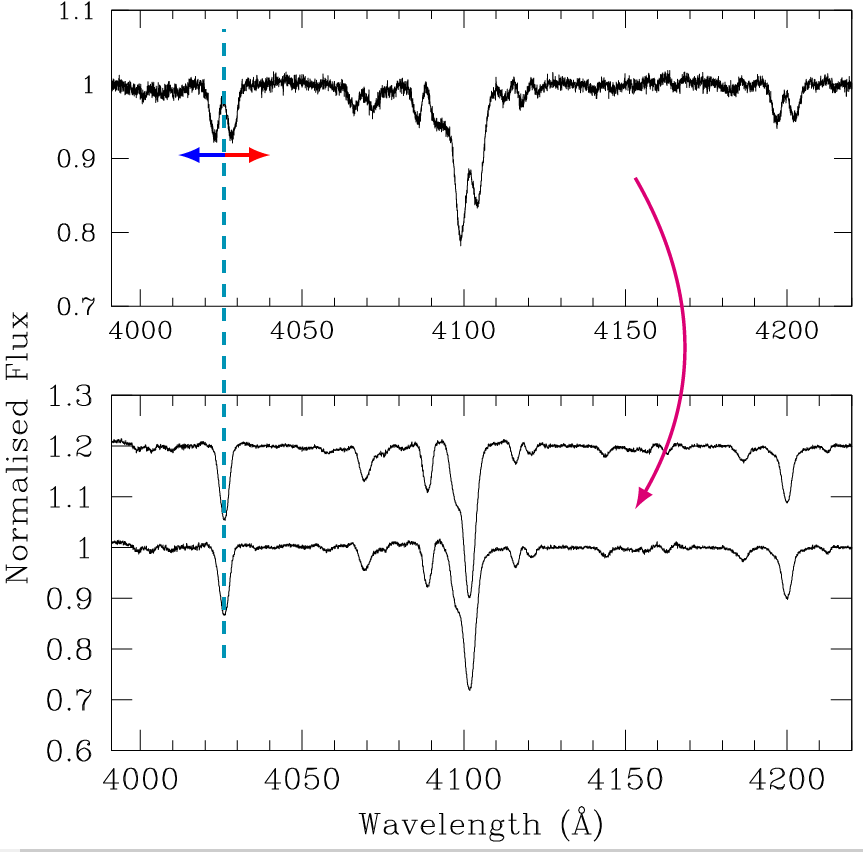
Figure 5.
Upper panel: one spectrum of HD152248 taken at an orbital phase at which the lines of the primary and secondary stars are well-deblended. Bottom panel: individual spectra of the primary and secondary stars obtained after disentangling (note that the spectrum of the secondary star has been shifted by +0.2 in the y-axis for convenience).
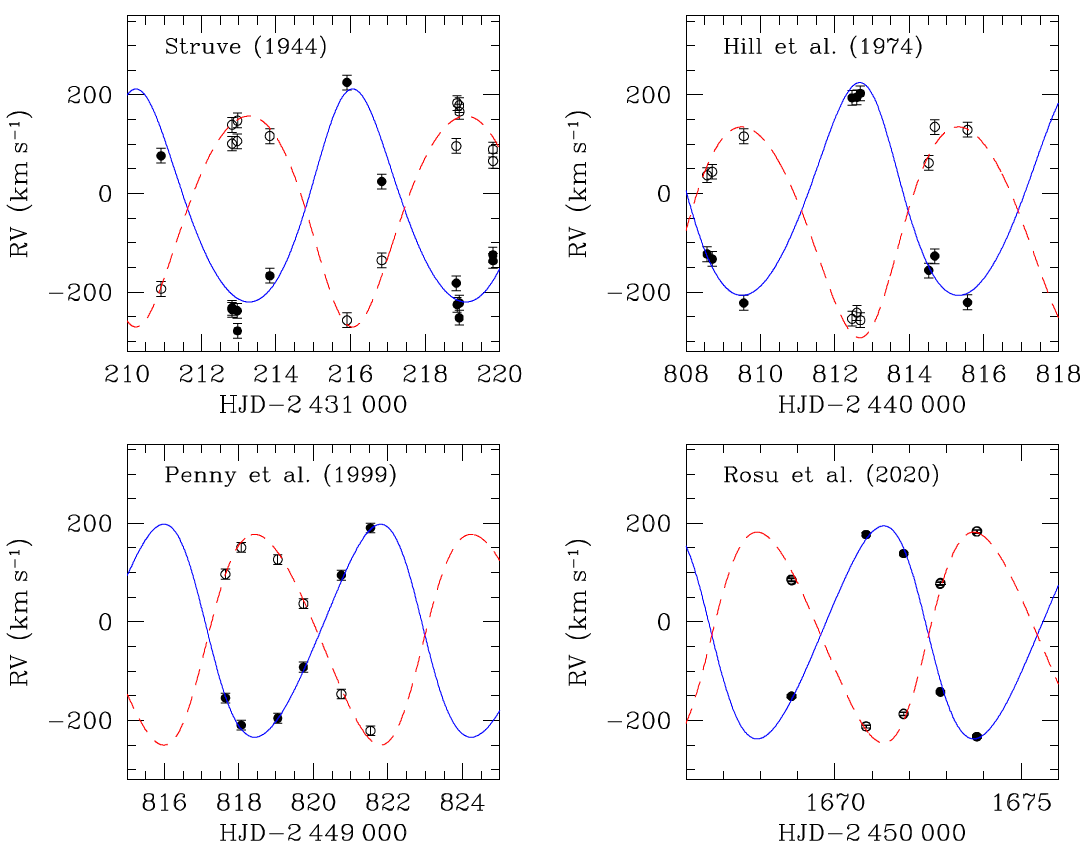
Figure 6.
Measured radial velocities of the primary (filled dots) and secondary (open dots) stars of the massive binary HD152248, and radial velocity curves obtained with the best-fit parameters. Top panels: data from [26] (left) and [27] (right). Bottom panels: data from [28] (left) and [16].
4. How apsidal motion is related to the internal structure of stars
22The simple two-body problem states that the apsidal motion rate of a binary system has a classical Newtonian contribution to which a general relativistic correction (GR) is applied:
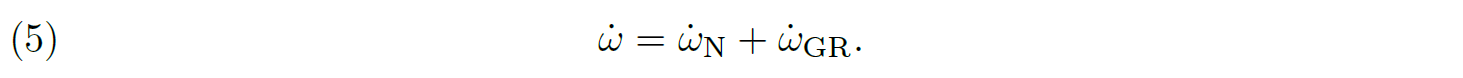
23The general relativistic correction to the apsidal motion rate takes the form
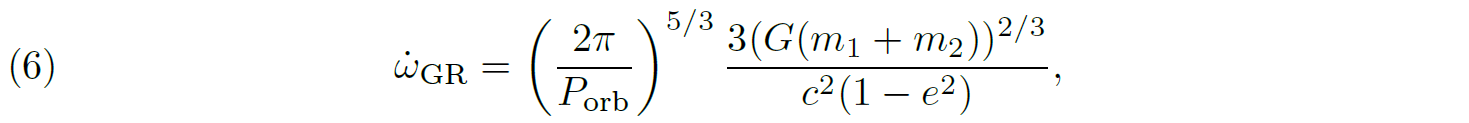
24where G and c denote the gravitational constant and the speed of light, respectively, and m1 and m2 are the masses of the primary and secondary stars, respectively [11].
25All the stellar parameters appearing in the expression of the general relativistic correction are known observationally, hence, the value of the general relativistic correction can be easily inferred. In general, this quantity is much smaller than the Newtonian contribution, except in a few special cases which are used to test the general relativity theory [29], exactly like Mercury was used at the beginning of the 20th century.
26The classical Newtonian contribution to the apsidal motion takes its origin in the non-Keplerian terms of the gravitational potentials of the stars. These terms stem from the non-spherical shape of the stars as a result of both the stellar rotation and the presence of the companion. Indeed, tidal interactions take their origin in the gravitational attraction existing between the two stars and in the stellar rotations which are not synchronised with the orbital motion. The amplitude of the deformation of a star in response to these tidal interactions depends on the way the mass is distributed in the stellar interior. The general expression of the Newtonian term takes into account the misalignment of the stellar rotation axis with respect to the normal to the binary orbital plane. However, it is highly unlikely that the rotation axis misalignment would be high for short-period binary systems. Hence, we restrict to the case where the stellar rotation axes are aligned with the normal to the orbital plane1.
271 A detailed analysis taking into account the stellar rotation axis misalignment is done in [30] for the short-period massive binary HD152248 and shows that unless a very high angle of ~60° is considered, the misalignment has no significant impact on the results.
28The Newtonian term is itself the sum of the contributions of the rotations of the two stars and the tidal deformation of each star induced by its companion. This term takes the following expression, as derived in [31]:
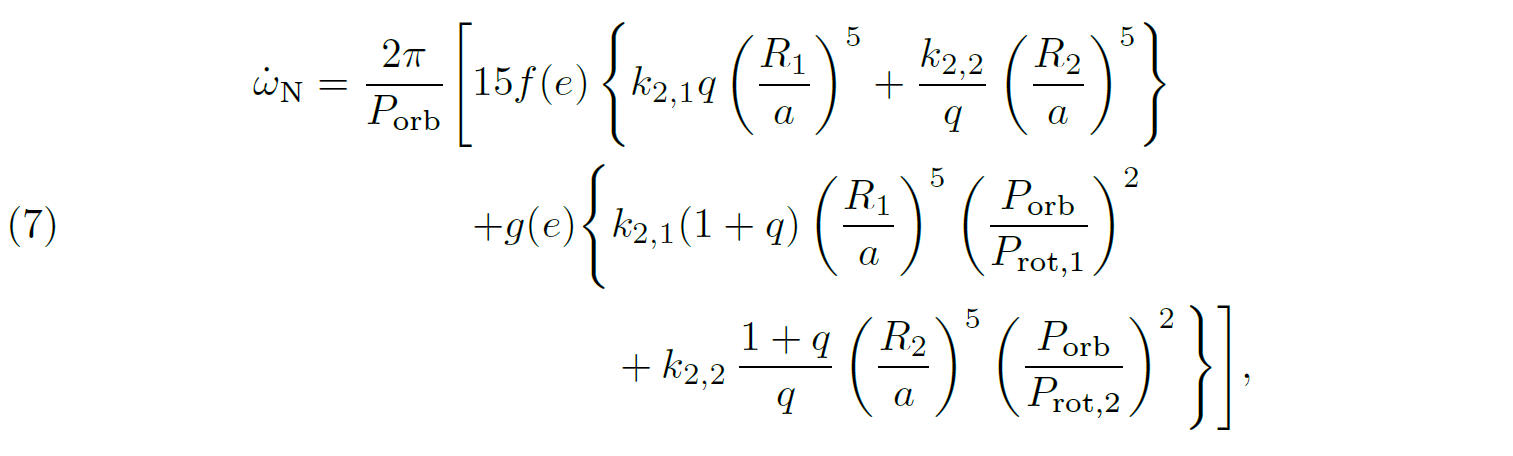
29where ɑ is the semi-major axis, q = m2/m1 is the mass ratio, R1 and R2 are the radii of the primary and secondary stars, respectively, k2,1 and k2,2 are the apsidal motion constants of the primary and secondary stars, respectively, Prot,1 and Prot,2 are the rotational periods of the primary and secondary stars, respectively, and f(e) and g(e) are functions of the eccentricity of the orbit. Their expressions are given by
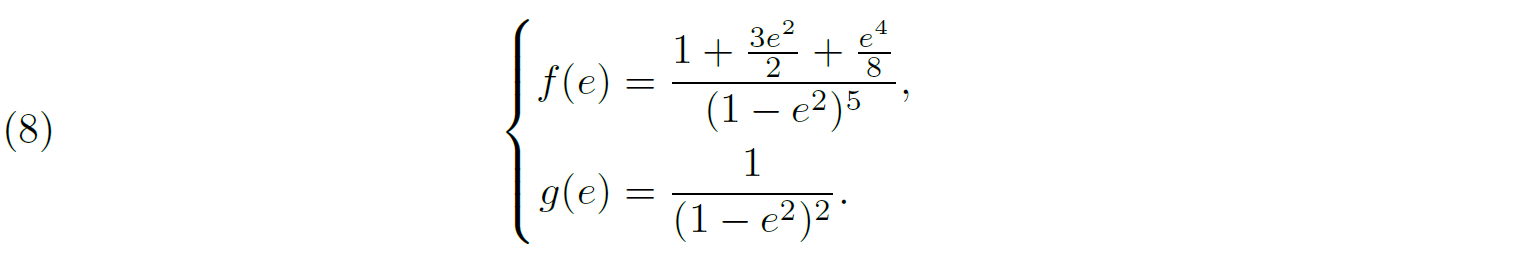
30With ω̇ and ω̇GR derived from observations, the Newtonian contribution can be constrained through Eq. (5). In expression (7), all terms can be inferred observationally, except for the internal structure constants of the stars. Indeed, the radii of the stars can be constrained through the light curve analysis, while the semimajor axis can be constrained through the radial velocity curve analysis, and therotational periods of the stars are derived from the width of the spectral lines.
31Also known as the apsidal motion constant, the internal structure constant k2 is a measure of the density contrast between the core and the external layers of the star. Its expression is given by
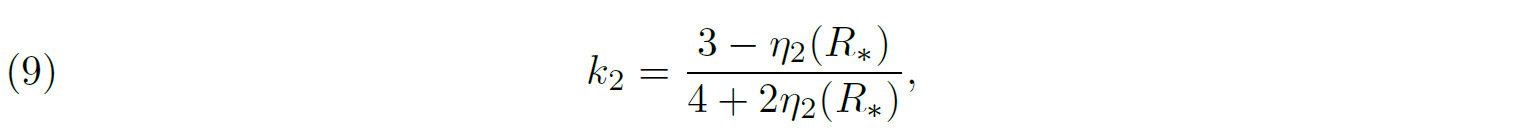
32where η2(R⁎) is the solution, evaluated at the stellar surface R⁎, of the Clairaut- Radau differential equation
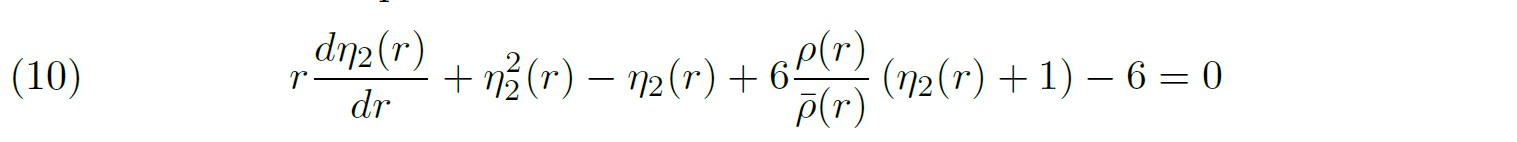
33with the boundary condition η2(0) = 0 [32]. In this expression, r is the current radius inside the star at which the equation is evaluated, ρ(r) is the density at the distance r from the center and ρ̅(r) is the mean density within the sphere of radius r.
34In Eq. (7), it is impossible to isolate the internal structure constants of the stars to observationally determine these, except if k2,1 = k2,2, in which case the two stars are identical and the binary system is a twin system. Such twin cases are scarce, but offer a unique opportunity to observationally constrain the k2-value. The massive binary HD152248, studied in detail in [16] is one such case where the k2-value could be inferred observationally.
35However, in the general case of two different stars, despite the fact that this parameter cannot be determined from an observational point of view, a small trick is generally used. We can rewrite Eq. (7) in the form
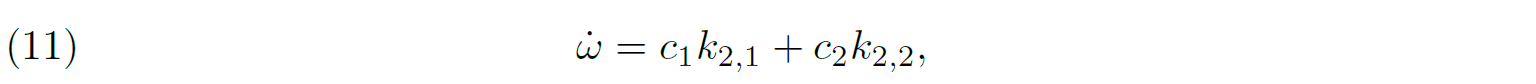
36where c1 and c2 are two known functions depending on the stellar parameters. We can then define a weighted average value of the internal structure constant for the system
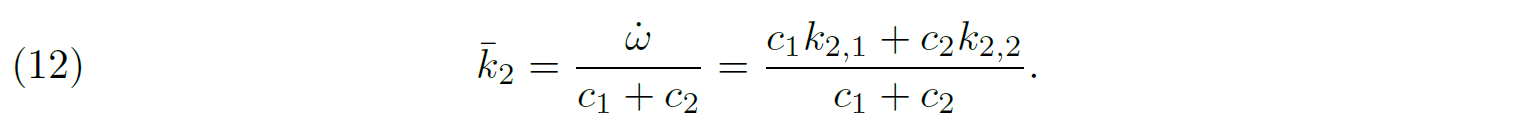
37This quantity can then be compared to the one obtained based on stellar structure and evolution models.
38The internal structure constant takes its maximal value of 0.75 for a homogeneous sphere of constant density and decreases towards values as low as 10-4 for massive stars which have a very dense core and a diluted atmosphere. As the density of the external layers decreases (compared to the core density) as the star evolves, k2 decreases, rendering this quantity a good indicator of the evolutionary state of the star.
5. A look at stellar structure models
39Stellar structure and evolution models aim at reproducing the internal structure of stars for a given set of initial parameters (or physical conditions) and for different evolutionary stages. In this way, we can follow the evolution with time of global stellar parameters (for instance the mass, radius, effective temperature, bolometric luminosity), as well as internal stellar parameters (for instance the size of the convective core, the density profile inside the star, and the central concentration of metals, among others).
40Several stellar evolution codes exist in the scientific community: to quote only three examples, the Code Liégeois d’Évolution Stellaire (Clés, developed and maintained by R. Scuflaire at the STAR Institute at the University of Liège [33]), the Geneva Stellar evolution code (GENEC, developed and maintained at the University of Geneva [34]), and the Modules for Experiments in Stellar Astrophysics code (MESA, developed and maintained at the University of California [35]).
41Each stellar evolution code has its own characteristics and specificities but the general physics implemented in these codes is usually very similar, just as the physical ingredients. For massive stars, which are our concern here, the stellar atmosphere can either be computed separately from the interior models and added as a boundary condition (as is the case in Clés) or directly computed with the stellar interior (as is the case in GENEC). The important mass-loss induced by stellar winds is implemented by default through the prescription of [36] but the user has the opportunity to scale this quantity by a multiplicative factor ξ or even to chose another formalism if deemed appropriate.
42The internal mixing is restricted to the convective core of the star, although additional mixing such as overshooting and/or turbulent mixing can be introduced in the model. Indeed, due to the inertia of chemical elements, some mixing also happens in a shell around the core (called the overshooting region). The overshooting is implemented as a displacement of the mixing region boundary towards the exterior from rc to rov through the simple step-function
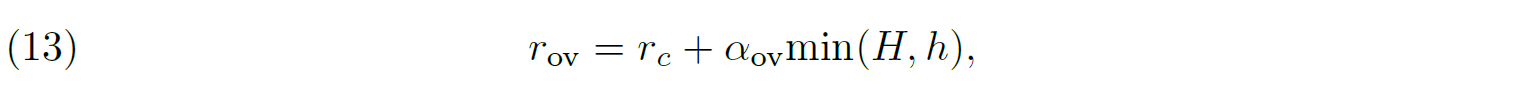
43where h is the thickness of the convective zone, H is a function of the pressure, density and gravity at the edge of the convective core, and αov is the overshooting parameter adopted by the user. When overshooting is added in the model, the mixed core is enlarged, and more fuel is available for the hydrogen fusion, hence the main-sequence lifetime of the star is extended.
44The turbulent transport of chemical elements is modelled as a diffusion process by adding a diffusion term to the velocity of the element. This diffusion term acts as reducing the abundance gradient of the element [37].
45Depending of the studied case and the user’s needs, one prefers to use one code or another. On the one hand, the GENEC code offers the possibility to explicitly include stellar rotation in the models, and it can take into account the mixing induced by tidal interactions in a binary system [38]. Although these two possibilities seem compulsory to properly model the internal structure of massive stars belonging to a close binary system undergoing tidal interactions, the reality is slightly less radical. Indeed, as shown by [30] in their analysis of the massive binary HD152248, the effects of rotational mixing on the stellar structure could a priori be simulated by enhancing turbulent mixing. These authors have also shown that, in the case of a well-detached binary such as HD152248, the inclusion of binarity in the code only accelerates the evolution of the stars along the evolutionary sequence they would follow if they were single [30]. On the other hand, the Clés code offers the possibility to determine the combinaison of free parameters allowing to best reproduce the chosen set of observational parameters of the star. Indeed, a Levenberg-Marquardt minimisation is implemented in the code as in [39]. The routine, called min-Clés, allows to put constraints on some parameters (such as the mass, radius, effective temperature, and luminosity, among others), while leaving some other parameters free (such as the initial mass and the age of the stars which are usually poorly constrained).
6. Review of some cases
46One of the best-known cases of apsidal motion among massive binary systems is certainly Y Cygni. Apsidal motion in this binary was discovered in the 1930’s by [40]. A detailed analysis of the apsidal motion was then performed by [41]. They determined a very low value of k̅2, (8.91 ± 1.44) × 10-3, which was very difficult to reconcile with the theoretical values obtained with the stellar evolution models of [42] and [43] available at the time of the study. The analysis of apsidal motion in Y Cygni was refined more recently by [44]. These authors used a large set of both spectroscopic and photometric data to constrain the fundamental parameters of the stars as well as to refine the value of the apsidal motion rate and the weighted-average value of the internal structure constant. The resulting values are summarised in Table 1. Their value of the weighted-average internal structure constant for the binary system, larger than the one determined by [41], agrees with the stellar evolution models of [45] which include more advanced physics and more precise opacity tables than those available at the time of [41].
47Another well-known case is the massive binary AG Persei, whose apsidal motion was discovered by [46]. As for Y Cygni, a detailed analysis of the apsidal motion was performed by [41]. The very low value of k̅2 they determined was also difficult to reconcile with theoretical models of [42] and [43]. This system has been reanalysed recently based on photometric data in [47]. The fundamental parameters obtained in this analysis, together with the refined value of the apsidal motion rate and the weighted-average value of the internal structure constant are given in Table 1. The k̅2-value they obtained observationally agrees with the theoretical value derived from the stellar evolution models of [48].
48CW Cephei is a well-known eccentric massive binary whose apsidal motion has first been mentioned by [49]. A detailed analysis has been performed by [41] who reached the same conclusions concerning the weighted-average internal structure constant of the binary as for the two previously mentioned systems. A refined analysis was performed recently by [47] (see Table 1) and it confirmed the k2-problem.
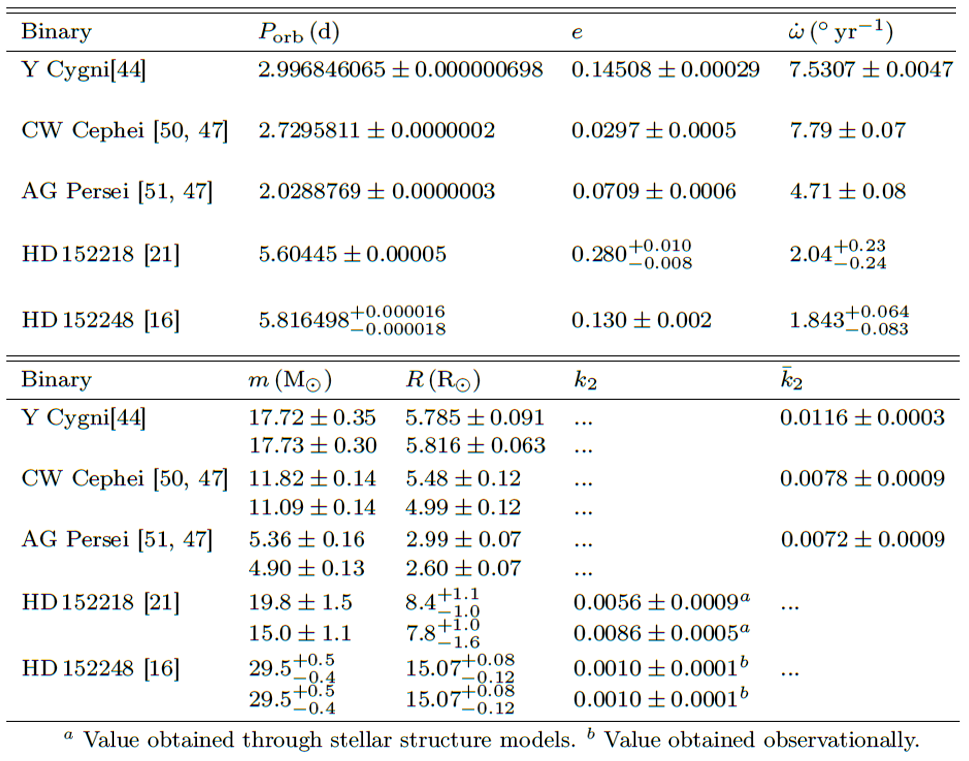
Table 1. Fundamental parameters of some binary systems for which apsidal motion has been studied in the literature.
Column 1 gives the name of the binary system as well as references. Columns Porb, e and ω̇ give the orbital period, eccentricity, and apsidal motion rate of the system, respectively. Columns m and R give the masses and radii of the primary (top) and secondary (bottom) stars. Column k2 gives the internal structure constant of each star, if available, whilst Column k̅2 gives the observational weighted-average internal structure constant of the binary, if individual k2 are not given.
49The three aforementioned systems experience apsidal motion at a fast rate compared to the majority of binary systems. The discovery of apsidal motion in other systems therefore had to wait until the instruments were precise enough and had been observed for a long-enough time to detect such a slow motion. Increased data acquisition over the last years allowed the study of numerous binary systems, which in turn allowed to detect new cases.
50To this aim, the GAPHE team of the University of Liège started to investigate massive binary systems belonging to the young open cluster NGC6231. Detecting apsidal motion in several systems belonging to the same cluster provides a sensitive test of our understanding of stellar structure and evolution as the chemical composition as well as the age of the stars should be the same.
51The first binary system which was studied is HD152218 [21]. The fundamental parameters of the stars are given in Table 1, together with the apsidal motion rate. As the two stars are different, the authors could not infer individual values for the internal structure constants, but rather inferred theoretical values for these parameters, based on Clés models available at that time.
52The second binary system of the cluster, HD152248, probably the most emblematic O-type binary in NGC6231, has been analysed very recently [16, 30]. The major and most valuable advantage of this binary system is the similarity of its two components, which allows to observationally constrain the individual values of the internal structure constants. Comparing to theoretical models computed with the Clés code, [30] constrained the masses, radii and positions in the Hertzsprung- Russel diagram to the observational values but allowed for different mixing sources. They concluded that an enhanced mixing was required, either through turbulent mixing or overshooting, to reproduce the fundamental parameters of the stars together with the apsidal motion rate of the binary and the internal structure constants. This result agrees with independent conclusions of other groups (see [52, 53], and reference therein), who found that standard stellar evolution models predict too homogeneous stars.
53Two more binary systems in NGC6231, namely HD152219 and CPD-41°7742, are currently under study. As these binaries are composed of two very different stars, the individual internal structure constants cannot be constrained. However, rather than computing a weighted-mean value for the internal structure constant of the binary system, we are currently working on the inclusion in the stellar evolution code of a constraint on the age of the two components of a binary system, forcing the two stars to have the same age. In this way, the degeneracy between k2,1 and k2,2 will, at least partially, be lifted.
54Finally, a completely different kind of analysis of the apsidal motion in a massive binary system can be mentioned: the extreme case of HD165052, reviewed by [54]. This binary system experiences apsidal motion at an extreme rate of (12.1 ± 0.3)° yr-1. The approach adopted by these authors is completely different from the one adopted elsewhere: rather than inferring the internal structure constant for the binary system on the basis of the apsidal motion rate, they deduced the masses of the components based on the apsidal motion rate. Due to the absence of eclipses in this system, these masses could not be inferred through photometry, hence apsidal motion became a way to infer masses in a binary system.
7. Conclusion
55The apsidal motion taking place in close eccentric binary systems is a phenomenon observed and measured for a couple of decades. This motion being very slow, a large set of observations spanning many years is required to obtain reliable estimates of the apsidal motion rate. But once such observational data are at hand, apsidal motion reveals precious and valuable information about the interior of massive binary stars. Such information is indeed difficult to obtain by other means. It not only reveals the density profile inside the stars, but also puts constraints on the internal mixing processes occurring inside the stars. It further allows to get an age estimate of the binary system and, when the binary systems under study belong to the same cluster, it allows to infer an age estimate for the entire cluster.
56Therefore, the study of apsidal motion in double-lined eclipsing binaries with non-zero eccentricity is a promising technique to probe the interior of stars from an observational point of view. These observational constraints serve as a basis to guide the refinement of the stellar evolution models. Such studies demonstrated that conventional models predict too homogeneous stars. With the advent of refined models, the discrepancy tends to decrease, but an entire knowledge of the interior of stars is still lacking. To achieve this goal, we need to enlarge the sample of binary stars for which such an analysis is performed.
Acknowledgments
57I warmly thank my colleagues Gregor Rauw and Yaël Nazé for their valuable comments towards the improvement of the manuscript. I acknowledge financial support from the Fonds de la Recherche Scientifique (F.R.S.-FNRS, Belgium).
Bibliographie
[1] F. Bresolin, P. A. Crowther, & J. Puls, Proc. IAU Symposium, 250 (2008)
[2] G. Duchêne, & A. Kraus, ARA&A, 51, 269 (2013)
[3] H. Sana, S. E. de Mink, A. de Koter, et al., Science, 337, 444 (2012)
[4] S. Ekström, C. Georgy, P. Eggenberger, et al., A&A, 537, A146 (2012)
[5] I. Brott, S. E. de Mink, M. Cantiello, et al., A&A, 530, A115 (2011)
[6] S. Wellstein, N. Langer, & H. Braun, A&A, 369, 939 (2001)
[7] D. Vanbeveren, C. De Loore, & W. Van Rensbergen, A&ARv, 9, 63 (1998)
[8] F. Raucq, E. Gosset, G. Rauw, et al., A&A, 601, A133 (2017)
[9] E. Moreno, G. Koenigsberger, & D. M. Harrington, A&A, 528, A48 (2011)
[10] J. H. M. M. Schmitt, K.-P. Schröder, G. Rauw, et al., A&A, 586, A104 (2016)
[11] N. I. Shakura, Sov. Astron. Lett., 11, 224 (1985)
[12] A. Claret, & A. Giménez, A&A, 519, A57 (2010)
[13] I. Bulut, & O. Demircan, MNRAS, 378, 179 (2007)
[14] A. Jones, Isis, 82, 3, 440 (1991)
[15] R. Wichmann, Astrophysics Source Code Library [record ascl:1106.016] (2011)
[16] S. Rosu, G. Rauw, K. E. Conroy, et al., A&A, 635, A145 (2020)
[17] A. Prša, K. E. Conroy, M. Horvat, et al., ApJS, 227, 29 (2016)
[18] D. Jones, K. E. Conroy, M. Horvat, et al., ApJS, 247, 63 (2020)
[19] P. Zasche, & M. Wolf, AJ, 157, 87 (2019)
[20] J. F. González, & H. Levato, A&A, 448, 283 (2006)
[21] G. Rauw, S. Rosu, A. Noels, et al., A&A, 594, A33 (2016)
[22] D. J. Hillier, & D. L. Miller, ApJ, 496, 407 (1998)
[23] A. E. Santolaya-Rey, J. Puls, & A. Herrero, A&A, 323, 488 (1997)
[24] T. Repolust, J. Puls, & A. Herrero, A&A, 415, 349 (2004)
[25] J. Puls, M. A. Urbaneja, R. Venero, et al., A&A, 435, 669 (2005)
[26] O. Struve, ApJ, 100, 189 (1944)
[27] G. Hill, D. L. Crawford, & J. V. Barnes, AJ, 79, 1271 (1974)
[28] L. R. Penny, D. R. Gies, & Jr. W. G. Bagnuolo, ApJ, 518, 450 (1999)
[29] A. Claret, & A. Giménez, A&A, 277, 487 (1993)
[30] S. Rosu, A. Noels, M.-A. Dupret, et al., A&A, in press (2020)
[31] T. E. Sterne, MNRAS, 99, 451 (1939)
[32] P. M. Hejlesen, A&AS, 69, 251 (1987)
[33] R. Scuflaire, S. Théado, J. Montalbán, et al., Ap&SS, 316, 83 (2008)
[34] P. Eggenberger, G. Maynet, A. Maeder, et al., Ap&SS, 316, 43 (2008)
[35] B. Paxton, L. Bildstein, A. Dotter, et al., ApJS, 192, 3 (2011)
[36] J. S. Vink, A. de Koter, & H. J. G. L. M. Lamers, A&A, 369, 574 (2001)
[37] J. Richer, G. Michaud, & S. Turcotte, ApJ, 529, 338 (2000)
[38] H. F. Song, A. Maeder, G. Meynet, et al., A&A, 556, A100 (2013)
[39] W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery, Numerical
Recipes in Fortran, Cambridge University Press (1992)
[40] R. S. Dugan, Contributions from the Princeton University Observatory, 12, 1 (1931)
[41] A. Giménez, C.-H. Kim, & I.-S. Nha, MNRAS, 224, 543 (1987)
[42] P. M. Hejlesen, A&AS, 39, 347 (1980)
[43] C. M. Jeffery, MNRAS, 207, 323 (1984)
[44] P. Harmanec, D. E. Holmgren, M. Wolf, et al., A&A, 563, A120 (2014)
[45] A. Claret, A&A, 424, 919 (2004)
[46] W. Chr. Martin, Bull. astr. Inst. Neth., 9, 416 (1938)
[47] M. Wolf, H. Kucáková, M. Kolasa, et al., A&A, 456, 1077 (2006)
[48] A. Claret, A&AS, 109, 441 (1995)
[49] I.-S. Nha, AJ, 80, 232 (1975)
[50] J. V. Clausen, & A. Giménez, A&A, 241, 98 (1991)
[51] A. Giménez, & J. V. Clausen, A&A, 291, 795 (1994)
[52] A. Giménez, J. V. Clausen, & K. S. Jensen, A&A, 159, 157 (1986)
[53] O. G. Benvenuto, A. M. Serenelli, L. G. Althaus, et al., MNRAS, 330, 435 (2002)
[54] G. Ferrero, R. Gamen, O. Benvenuto, & E. Fernández-Lajús, MNRAS, 433, 1300 (2013)