- Portada
- Volume 90 - Année 2021
- Articles sur invitation - Invited papers
- Evaporation of superparamagnetic colloids
Vista(s): 1807 (76 ULiège)
Descargar(s): 122 (2 ULiège)
Evaporation of superparamagnetic colloids
Article sur invitation – Invited paper

Documento adjunto(s)
Version PDF originaleRésumé
L’évaporation de ce qu’on appelle des colloïdes, c.-à-d. des liquides contenant des particules (sub)micrométriques, est un phénomène omniprésent. De la tache de café à la peinture de nos murs, en passant par les taches de sang sur les scènes de crime, les dépôts séchés vont de la saleté au revêtement utile, en passant par les indices dans les affaires criminelles. Les mécanismes de structuration de ces dépôts font donc l’objet d’une recherche intensive. Parmi les propositions récentes, des colloïdes magnétiques ont été proposés comme système modèle. En effet, leurs interactions peuvent être contrôlées par un champ magnétique externe, agissant comme une télécommande des propriétés de la suspension, Le présent article passe en revue les résultats les plus récents concernant une sous-classe spécifique définie comme des colloïdes superparamagnétiques. Il a été rédigé pour un public scientifique non expert. Une introduction générale au domaine de l’évaporation des colloïdes est suivie par une description des propriétés des colloïdes superparamagnétiques. Les dernières sections offrent un aperçu des conditions dans lesquelles un contrôle de la structure des dépôts d’évaporation des colloïdes superparamagnétiques peut être réalisé.
Abstract
Evaporation of so-called colloids, i.e. liquids containing (sub-)micrometric particles, is an omnipresent phenomenon. From the stain of coffee to the painting of our walls, via blood stains on crime scenes, the dried deposits they leave range from dirt to useful coating, via clues in criminal cases. The mechanisms behind the structuring of these deposits are then a topic of intensive research. Among recent proposals, magnetic colloids have been proposed as a model system. Indeed, their interactions can be controlled through an external magnetic field, acting as a remote control of the suspension properties. This paper reviews the most recent results regarding a specific subclass defined as superparamagnetic colloids. It has been written for a non-expert scientific audience. This review starts with a general introduction to the field of colloids evaporation, then describes the properties of superparamagnetic colloids. In its last sections, it offers an overview of the conditions in which a control of both the broad and detailed structures of superparamagnetic colloids evaporative deposits can be achieved.
Tabla de contenidos
Cet article a reçu un des deux Prix Annuels 2020 de la Société Royale des Sciences de Liège. This paper was awarded one of the two Annual Prizes 2020 of the Société Royale des Sciences de Liège,
Received 13 November 2020, accepted 15 March 2021
1. Introduction
1What is the common point between ink, paint, blood, and coffee? People with a background in multiphase systems would answer pretty fast that they are colloidal systems: sub-micron particles suspended in a continuous fluid. But that’s not all. Indeed, the solid deposit left after evaporation of their liquid part has attracted an enormous amount of research for each of them. Regarding coffee, it is often considered as waste or dirt, and many studies have shown how to prevent or remove this deposition through self-cleaning surfaces [1-3]. However, it is the main purpose of paints and inks to leave a clear trail, and their deposition gathered much attention due to their various applications [4-7], sometimes requiring control of the deposits at microscopic scale [8-10]. Lastly, blood deposits are sources of information on crime scenes [11,12], and are foreseen as a possible diagnostic tool [13-19]. For these reasons, and many others, the evaporation of colloidal droplets on a solid substrate is currently a topic of intense fundamental research [20-27].

Figure 1. Typical coffee-stain, as observed in a dirty sink of an academic office.
The stains are darker near the edges, indicating a higher concentration of solid particles in these areas.
2These studies highlighted the robustness of an effect, called “coffee-ring effect”, which often prevents a fine control of the deposit [28-30]. This nickname emphasizes the fact that particles tend to migrate to the edge of an evaporating droplet, which leads to a ring-like deposit as typically observed in every-day coffee stains (see Figure 1). This ring arises from an inhomogeneous evaporation rate, inherent to the geometry of the sessile droplet. Indeed, the curvature of the surface is usually higher near the edge. This induces a peak-effect of the evaporation rate, similar to the electrostatic peak-effect, creating a higher evaporation rate near the edge [28,29]. But at the same time, the surface tension of the liquid constraints the surface to keep a spherical cap shape near the edge, with a pinned contact line... The liquid has then no choice, but flowing from the center to the edge of the droplet to replenish the liquid that has been evaporated in excess overthere, as illustrated in Figure 2. This flow then drags along the suspended particles, which end up accumulating near the edge of the deposit.
3Many studies have focused on ways to suppress this coffee-ring effect [31-35]. One of the most famous and convenient successful cases is paint. In order to stabilize the colloidal pigment deposition, manufacturers add so-called “binders” (typically, polymeric resins) to the suspension, in order to fix the pigment uniformly on the deposit [36]. However, those binders modify many other properties of the suspension, such as its viscosity and drying time [37,38]. In particular, the drying time of the paints usually increases with the concentration of binders [39]. While this might be useful to mix successive brushstrokes, limiting the drying time might also be critical in some applications. Everyone who ever sat down on a freshly painted park bench can probably testify about it... Once again, industries have found ways to modify the drying time thanks to so-called “dryers” (often metal-based organic salt, interacting with the solvent or the binder) [40], but all these modifications and additions of components make the paints more expensive, more complex to produce and harder to model.
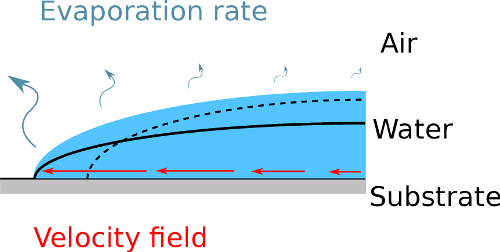
Figure 2. Illustration of the mechanisms leading to the coffee-ring deposits.
The evaporation rate, represented by the curvy arrows, is higher near the edge of the droplet, which typically has a greater curvature. If the liquid was not moving, the surface between air and water would become the dashed line. However, the contact line is pinned and the surface tension constrains the surface to the black line. The fluid is then flowing outward as indicated by the straight arrows.
4For simpler suspensions, another way to modify the distribution of colloidal particles in a dried deposit is to tune the ionic composition of the solvent. Indeed, the surface of colloidal particles is often electrically charged. Various mechanisms can create this charge, such as ions adsorption or direct ionization. [41-43] This surface charge then creates an electrical repulsion between the particles, which is in competition with the Van der Waals attraction. Moreover, the ions already present in the suspension can screen the electrostatic repulsion, creating in total a complex energy landscape. This complex interaction is usually modeled by the so-called DLVO potential [41-47]. The DLVO interaction exists between the different colloidal particles, but also between the particles and the substrate. If the substrate is attractive enough, and even if it might be limited to a small-range interaction, this attraction can then compete with the drag force of the coffee-ring flow. Some studies have then shown that the pH can modify the density profile of the colloidal dried deposits [48]. However, even if the pH is fixed with some buffer, the ion concentration itself has shown to have a tremendous effect on the deposit’ structure [49-51], as illustrated in Figure 3.

Figure 3. Comparison of dried deposits with two different dilutions of a pH buffer as suspending liquid. The pH buffer is Phosphate Buffered Saline (PBS), a preparation with well-defined concentration of several non-organic ions. The initial volume fraction of PBS diluted in distilled water is indicated as the parameter κ0. As one can see, when the ions concentration increases, the deposit is more homogeneous.
Reprinted figure with permission from [49] (DOI: http://dx.doi.org/10.1103/PhysRevE.98.062609 ). Copyright (2018) by the American Physical Society.
5Another effect which is often occurring in evaporating droplet is a Marangoni flow [32-34,48, 52-54]. This kind of flow, by definition, is produced by a gradient of surface tension. Such gradients have first been observed as a result of temperature gradients, resulting from both inhomogeneity of the evaporation rate along the surface (evaporation being an endothermic process), and heat transfer from the substrate [32,52]. Given the actual conditions of temperature, substrate and liquid thermal conductivity, this recirculation can hinder or reinforce the coffee-ring flow. The eventual deposit, with such temperature-induced Marangoni flow, can then range from the usual coffee-ring pattern to a deposit where most of the particles lie in the middle of the deposit [32,48,52]. But it has also been shown that Marangoni stress can appear due to the presence of surfactants or bulk-tensioactive agents in the liquid [33,34,49-51,53-55]. In those cases, the recirculation can also be triggered as an instability, where several recirculation cells are observed along one radius of the droplet [33,34,53,54]. This kind of instability usually tends to decrease the coffee-ring effect. Another feature which can be created by Marangoni recirculation is the so-called Marangoni eddy [54]. Actually, the Marangoni recirculation near the edge of the droplet and can rearrange a part of the particles from the coffee-ring. This creates a secondary peak of density in the deposit, a bit further from the edge. This kind of flow can then have a tremendous impact on the properties of the dried deposits.
6However, all the previous techniques focused on the suspensions composition, each suspension then giving rise to only a fixed set of properties for the deposits, including structure, resistivity and opacity. While reproducibility might be useful for industrial applications, flexibility could also be advantageous in some cases. This is particularly true if one wants to use a model system whose characteristics can be continuously tuned, possibly in real time.
7To this end, it has recently been suggested to use magnetic colloids as a model system, where the external magnetic field can be used as a remote control [56-58]. In the particular case of superparamagnetic colloids, it has been shown that this remote control can then tune the properties of the deposit, through inter-particles interactions [59]. This could lead to some applications in surface texturing, but also offers an ideal model system to understand the influence of particles interactions on the resulting dried deposits. This paper presents a review of some results obtained with such system, aimed at a non-expert scientific audience. The next section makes a brief review of what are superparamagnetic colloids and their known properties.
2. Super-paramagnetic colloids
8Superparamagnetic colloids are magnetic nanoparticles (being a magnetic monodomain) inserted in a matrix of non-magnetic material (usually polystyrene or silica) to obtain particles with diameter ranging from 100 nm to a few micrometers [61]. This core is then surrounded by a diamagnetic shell. This shell makes that the particles can be assimilated as magnetic dipoles, without taking into account the details of the core structure, even when two particles are touching each other [60]. Such a structure is illustrated in Figure 4. The paramagnetic properties of the whole particle come from the fact that there is no long-range order between the ferromagnetic inclusions. The small size of these inclusions implies a low magnetic energy. They are consequently already superparamagnetic. Indeed, thermal agitation can reverse their magnetic orientation on a time scale much smaller than the observation time. The time required to reverse this orientation is called the Néel time and highly depends on the material and the size of the sample [62]. Without external magnetic field, the colloidal particle has thus no remanent magnetic moment, which is characteristic of paramagnetic materials. When immersed in a magnetic field, it gets a reversible induced magnetization because the orientation of the magnetic moment of each nano-inclusion acquires a preferential direction along the field. The strength of their response to external magnetic fields, i.e. their magnetic susceptibility, is close to the order of ferromagnetic materials [60,63,64]. The magnetization process of a superparamagnetic colloidal particle is illustrated in Figure 5.
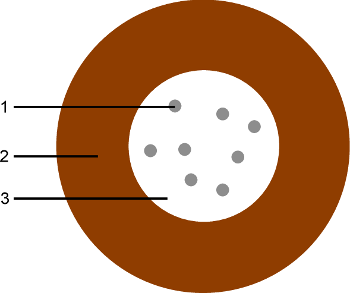
Figure 4. Characteristic structure of a superparamagnetic coilloidal particle.
1: Inclusion of ferromagnetic nanoparticle 2: Diamagnetic shell. 3: Superparamagnetic core, containing the ferromagnetic nano-inclusions in a diamagnetic matrix. Practically, the diamagnetic matrix and the shell can be made of the same diamagnetic material, depending on the manufacturing process. The surface of the shell can be covered with functional groups, for specific applications or in order to stabilize the suspension [60].
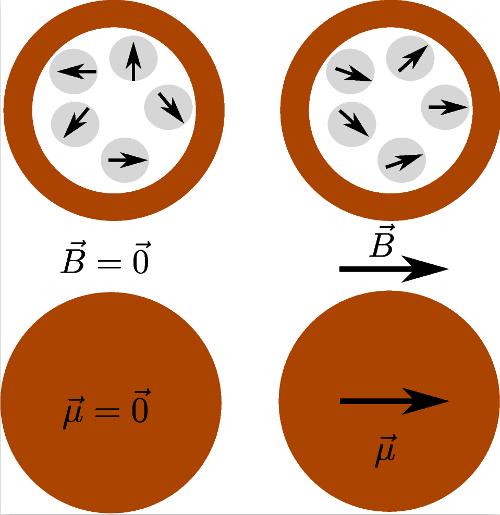
Figure 5. Illustration of the magnetization process of a superparamagnetic particle.
The fluctuating magnetic moments of the nanoinclusions are pictured in the above schemes, their average orientation depending on the external magnetic field. The global magnetic moment of the particle is represented by an arrow in the bottom schemes.
9In applications, the surface of superparamagnetic colloids is functionalized to capture specific targets, which can then be manipulated through magnetic fields. This leads to several applications such as protein isolation, cell separation, waste capture, bacteria processing, chromatography, etc [63, 65-74]. This flexibility, added to the remote manipulation through magnetic field, makes them a class of extensively used particles [68].
10One of the most interesting aspects of those magnetic colloids is that they interact not only with the external magnetic field, but also with each other. Indeed, each particle behaves like a tiny magnet, once there is an external magnetic field. Those tiny magnets then interact together, as paper clips or nails do once one of them touches a macroscopic magnet. This interaction leads to self-assembled structures and can be very helpful in some applications. For example, the magnetophoresis of those particles can be order of magnitude more efficient than expected, partly thanks to these assemblies [75]. Those chains can also serve as the basic components of more complex assemblies, possibly used as microbots [76-79]. Next section describes the processes of superparamagnetic colloids’ self-assembly when a uniform magnetic field is applied on a sample.
3. Self-assembly
11As explained earlier, the superparamagnetic colloids interact as magnetic dipoles μ, when they are immersed in an external magnetic field B. Moreover, their orientation is fixed by this external magnetic field, as well as their magnitude. Indeed, for magnetic field low enough, there is a linear relationship between both of them. One can then write the magnetic interaction potential between two of those magnetic dipoles in a simplified way as
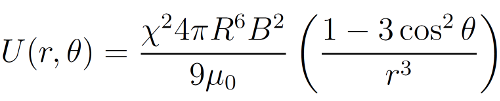
12where R is the radius of the particles, χ their magnetic susceptibility, μ0 the magnetic permeability of the vacuum, r their distance and θ = cos-1 (ez·er), if ez is the unitary vector pointing in the direction of B and er is the unit vector in the direction joining the two particles [61,69]. This potential, along with the previous variables, is represented in Figure 6.
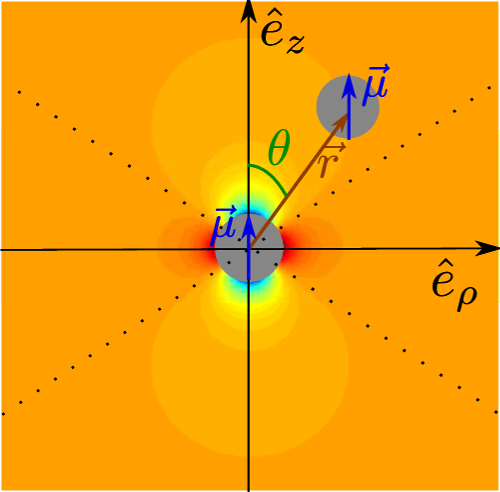
Figure 6. Diagram of the magnetic interaction potential. The different parameters of U(r,θ) are illustrated in this diagram. The background shading indicates the value of at each point, from black (very negative) to white (very positive). The main gray color denotes a negligible magnetic energy. The dotted lines separate the zones of radial attraction and repulsion. The zones containing black areas are the ones where radial attraction occurs.
Figure adapted from [80] (DOI: https://doi.org/10.1119/1.4975382 ), with the permission of the American Association of Physics Teachers.
13This interaction notably implies that, if two particles are immersed in a constant and uniform magnetic field B, they reach a stable configuration when they touch each other and are aligned with this external field B. Indeed, the minimum value of their interaction energy is reached when θ = 0 or π, and r is minimal (i.e. r = 2R for solid particles). This might lead the particles to self-organize into chains aligned with the field [61,63,69,70,81-84]. This process is illustrated in Figure 7. Moreover, this aggregation is reversible, meaning that the chains break up if the magnetic field B is suppressed, due to their almost zero remanence [70,80,85]. Experimentally, chains of several particles are typically observed [61,81,83] and the growth is successfully described on short time (typically up to 300s) by a Smoluchowsky equation, predicting a power law behavior of the mean size of the chains <s> ∝ tz after a transient behavior [61, 81-84]. Such chains can be useful in applications since they enhance the magnetophoresis of the particles [60,63,75] and can serve as the basis of more complex structures or microbots [76-79].

Figure 7. Left: Sketch of an experimental set-up used to observe self-assembly of superparamagnetic colloids. A transparent chamber containing the colloidal suspension is placed between two coils generating a constant and homogenous magnetic field B. The sample is enlightened from the top and observed from the bottom thanks to an inverted microscope. Right: Evolution of the chains formation along time as observed in experiments from [86]. One can observe the formation of chains aligned with the external magnetic field.
Figure reproduced from [86], with kind permission of The European Physical Journal (EPJ) (Copyright EPJ (2016)).
14However, the growth of those chains does not last forever. Actually, the competition between magnetic attraction and the mixing entropy of the system, which tends to maximize the number of various chains, will limit the average size of the structures. The suspension will eventually reach a thermodynamic equilibrium, characterized by a minimum of the free energy of the system [62, 69, 86, 87].
15Moreover, recent research has shown that those linear structures are not the only one observed [62, 86]. Indeed, long chains of more than 15 particles long tend to aggregate side-by-side. This might sound surprising at first thought, because first neighboring dipoles from two different chains interact repulsively. However, the interactions with further neighbors of the other chain are all attractive, and when the chains are long enough, theses attractions exceeds the repulsion of closest neighbors. This transition is illustrated in Figure 8.
16From a fundamental perspective, one can also see from the graph in Figure 8 that the energy par particle saturates at a finite value for a linear chain, as both highlighted in numerical simulations [62] and justified theoretically [88]. However, the addition of lateral neighbor does not lead to such a saturation of energy gain per particle, which is the fundamental reason for the apparition of these ribbons [88].
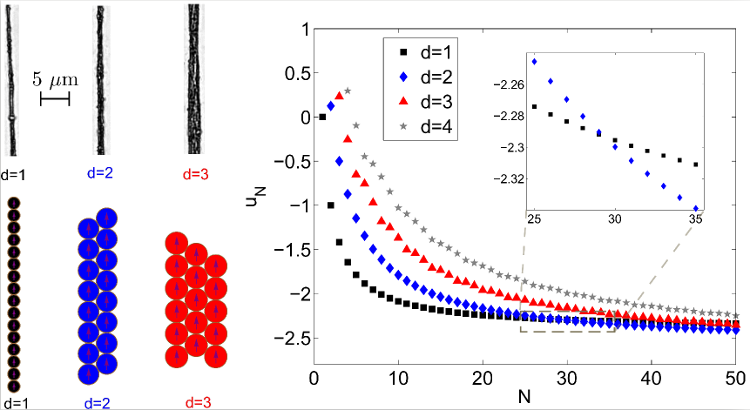
Figure 8. Top Left: experimental pictures of structures wider than one colloidal particle. Bottom Left: idealization of the structures, used to compute the magnetic energy per particle. Right: Evolution of the magnetic interaction energy per particle uN, as a function of the number of particles in the structure N, for structures with various widths. One can see that the wider structures reach lower energies for high number of particles, the first transition occurring at 30 particles. This means that two side-by-side chains of 15 particles have a lower magnetic energy than a linear chain of 30 particles.
Pictures adapted from [86], with kind permission of The European Physical Journal (EPJ) (Copyright EPJ (2016)).
17Another aspect enhancing the unexpected complexity of the suspension of such self-assembled chains is their dependency on the volume fraction. It was initially believed that only the interactions between single particles in a given aggregate, chain or ribbon, had to be taken into account to describe the equilibrium of the system [63,69]. However, recent numerical simulations, supported by experiments, showed that, at high volume frac-tion, the long-range interaction between various chains, which is repulsive, also has to be taken into account [89]. It has been demonstrated that a “two-levels” mean field theory could reproduce the behavior of such system. This theory defines one mean interaction for the particles inside a given aggregate, and another mean interaction for the repulsion between different aggregates [89].
18Overall, there is currently no analytical model able to take into account the presence of more complex aggregates, as those illustrated in Figure 8, in the thermodynamic equilibrium. This means that, nowadays, analytical models accurately predict the equilibrium properties only for small magnetic fields. Actually, even numerical simulations have difficulties reproducing realistic systems showing this behavior. Indeed, classical techniques of numerical simulations (Langevin dynamics, molecular dynamics, soft sphere discrete element methods,...) would require several years of computing time to reach equilibrium state with enough particles to form a statistically relevant amount of long chains [62,69]. Numbers currently report that actual experiments last for hours and one second of simulation currently takes from 300 to 1100 hours of computing time [69]. The most recently published simulations used some alternative techniques, performing further assumptions on the system. One of these assumptions is to consider the aggregation of the particles as irreversible and use a simplified magnetic interaction.
19This requires to dynamically redefine the objects in the simulation and implies a progressive decrease of their number. This progressive decrease in the number of objects in the system then shortens the simulations [62]. However, the assumption of irreversible aggregation is only valid when the magnetic interactions are really high and the system is diluted, which limits its range of application. Another proposed solution is to decrease the viscosity of the surrounding fluid [87]. Indeed, it has been shown that, above a certain threshold computable with a Péclet number, a decrease of the viscosity accelerates the reach of the thermodynamic equilibrium, without modifying its properties [89]. Unfortunately, even if they gave access to higher volume fraction than previously, those simulations couldn’t reach equilibrium containing ribbons of colloids. This experimentally observed state is thus a current challenge from both theoretical and numerical points of view.
20However, these interactions, depending on an external field and leading to self-assembled structures, can then be exploited experimentally in the evaporation of colloidal’s droplet. Indeed, the magnetic field acts as a remote control for the interactions between the particles. It is then a flexible way to modify the structures which appear in such suspensions [59]. The question is to what extent those structures have an influence on the final dried deposit. The next section describes the current results about this topic.
4. Evaporative deposits
21As explained earlier, the dried deposits of superparamagnetic colloids highly depend on the composition of the suspending liquid. With a low concentration of ions, the deposit presents a strong coffee-ring effect. However, with a higher concentration of ions, the deposit is already much more homogeneous, as shown in Figure 3. As already stated, this might be understood by taking into account the fact that ions screen the electrostatic repulsion and favor the Van der Waals attraction. The attractive behavior occurs between the various particles but also between particles and substrate. This has then two effects on the system [49, 90]. The first one is that particles are more likely to form aggregates which can then sediment. Therefore, the particles are more likely to be close to the substrate and interact with it. The second effect is that the interactions with the substrate are more likely to counteract the drag force of the flowing liquid, then potentially counteracting the coffee-ring effect.
22Moreover, the PBS has a small tensioactive effect. Indeed, surface tension of PBS slightly increases with the PBS concentration [90]. Since the outward flow due to the coffee-ring creates a gradient of concentration, it also induces a higher surface tension near the edge of the droplet. This, which could at first sight tend to reinforce the outward flow [55], can also actually trigger a Marangoni instability [49, 51]. This instability consists of several recirculation cells, which homogenize the particles distribution, but also traps particles near the surface in a “honeycomb-like” structure [49]. The characteristic size of this structure decreases with Marangoni stress, and then with PBS concentration. This explains the bigger clots of particles in the middle of the deposit for low PBS concentration in Figure 9. For higher PBS concentration, the structure has much smaller components, which remain almost as is in the eventual deposits thanks to the substrate attraction. For low concentrations, the structure however looses most of its integrity at the end of the evaporation process, since the substrate is not attractive enough to counterbalance the final stage of outward flow.
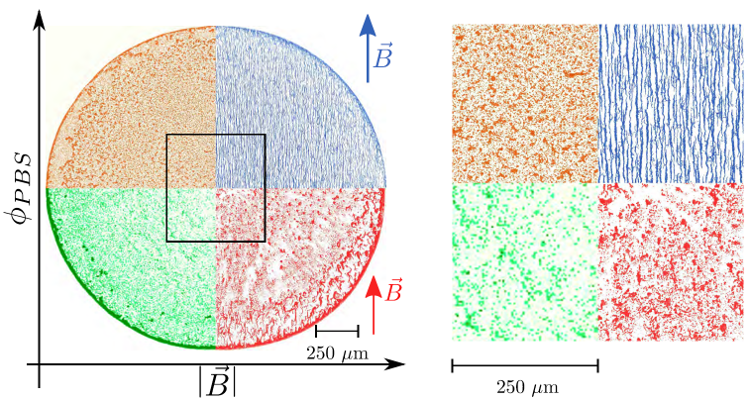
Figure 9. Various deposits obtained when varying both the magnetic field and the concentration of ions (indicated by κ0, the initial volume fraction of PBS, which is diluted in distilled water). One can see that the ions can prevent an overall coffee-ring effect. The magnetic field reinforces this prevention and also creates a detailed structure at a smaller scale.
Figure reprinted from [90] (DOI: https://doi.org/10.1016/j.colcom.2019.100198 ), with permission from Elsevier.
23The self-assembly of the particles has then a similar outcome of counteracting the coffee-ring effect through interactions. Indeed, aggregates formed through the magnetic interactions of the particles also tend to sediment. The density of the particles near the substrate is then furthermore increased. However, if the interactions with the substrate are not attractive enough, the temporary deposit will not resist the drag from the liquid flow. This drag then destroys the self-assembled structures, and the eventually dried deposit has a structure close to a typical coffee-ring. However, when there is both an external magnetic field and a high concentration of ions, the self-assembled structures can resist this stress and the eventual deposit keeps the structures created by the magnetic field [90]. This then leads to a rich phase diagram, as represented in Figure 9. The deposition of these self-assembled structures is not limited to the homogeneous and constant magnetic fields. More complex fields, such as rotating or oscillating ones, have also demonstrated the possibility to create aggregates which can be deposited almost as is [59]. Such deposits are represented in Figure 10. The influence of the magnetic field is then twofold. First, it changes the overall particles distribution in the dried deposit, by increasing the importance of sedimentation through agglomerating particles. Second, it also creates a fine structure at a smaller level, by self-assembling the particles in aggregates of specific shapes, depending on the intensity and temporal properties of the field.
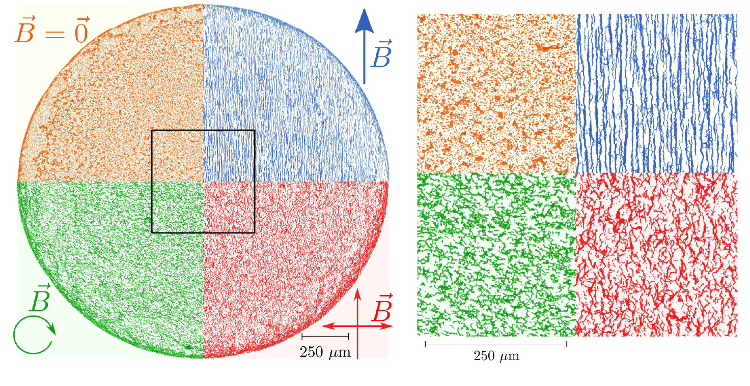
Figure 10. Dried deposits obtained with a “high” concentration of PBS (initial dilution κ0 = 50.10−3) and various magnetic fields. As one can see, the deposits contain the self-assembled aggregates of particles, almost as is from the suspension. This means that the magnetic field acted as a remote-control for these dried structures.
Reprinted figure with permission from [59] (DOI: http://dx.doi.org/10.1103/PhysRevE.98.062608 ). Copyright (2018) by the American Physical Society.
24In other words, this field act as a remote control. It gives possibilities to tune global and local properties of the deposit. It then has an influence at all the different scales of the system. And one can also adjust the global properties of the deposit by adjusting the ions concentration. Evaporating superparamagnetic colloids are therefore a system which is very flexible, offering opportunities to choose the eventual dried deposit during the evaporation process. This also leads to various possible deposits for a single suspension of particles, chosen through the properties of the external field. Moreover, it has already allowed to make significant steps in the comprehension and modeling of the mechanisms governing the distribution of colloidal particles in evaporative deposits [59, 90].
5. Conclusion and perspectives
25Recent publications on self-assembling superparamagnetic colloids have evidenced how analytical models compare with actual experiments. While the models are efficient to predict thermodynamic equi-librium for chains of particles in low magnetic fields and limited volume fractions [69, 89], the presence of more complex structures for higher magnetic field makes the experimental situation harder to fully comprehend [62, 86]. In particular, situations with high magnetic fields and large aggregates are nowadays still challenging to model, due to the various geometries available to the aggregates. Given the intrinsic interest of the magnetic structures for several applications, such as magnetophoresis filtering or remote-controlled microbots [60, 63, 75, 77-79, 91], further insight in this topic would certainly provide a better grasp of those applications. Indeed, the first step to assemble magnetic microbots is often to produce well-defined aggregates of colloids [76-79]. Those microbots are seen as having an interesting potential for medical applications (e.g. for drug delivery or bacteria killing [92-95]) as well as for water filtering [94-96]. Understanding and mastering a method of self-assembled production of magnetic colloids is then a crucial step towards the development and efficiency of such a micro-technology in those areas.
26In addition, the current knowledge about superparamagnetic colloids already leads to a good un-derstanding on their evaporative deposits. A detailed description of their structure, both on global and local scale, is already available and supported by theoretical scalings [59, 90]. Given the importance of sedimentation on this system, it might however be interesting to go further and try new configurations. For instance, nobody never focused on what happens when the evaporating liquid is not on top but below the solid substrate. Very different results can be expected since the sedimentation would then lead the particles toward the air-liquid interface instead of the substrate. The effect of the tilting of the substrate should be interesting to investigate. And there are still so many possible configurations of the external magnetic field to explore... One can tilt the field, modify it during the evaporation process, either on time scales close to the evaporation time or to the particles’ assembly characteristic time, which can differ from several orders of magnitude... On a more fundamental level, some questions remain challenging. There is indeed currently no mechanistic model to predict quantitatively the distribution of the particles in the eventual dried deposit. Such a model would require to first understand in details the competition between the drag of the fluid flow and the attraction of the substrate as well as how the presence of aggregated particles modifies the flow itself.
27Such fundamental understanding would likely help to reach some of the more promising applications regarding the controlled deposition of colloids. For instance, the controlled patterning of colloids deposition can lead to some enhanced wettability properties [97-99], which is a key parameter to prevent raindrops, snow or fog adhesion to surfaces such as windows, antenna or self-cleaning devices [100]. Surface structuring has also been shown to modify the properties of field-emitter devices, allowing to optimize the turn-on time, compactness and sustainability of devices such as displays or antennae [101, 102]. The modification of the surface area and structure can also lead to catalytic properties for chemical or (cell-based) biological reactions, which might be useful to grow artificial organic tissues [100, 103]. Moreover, optical properties of the covered surfaces are also modified by the deposition, which can be used to produce light filters or anti-reflection surfaces [100, 104].
28Moreover, the deposit that magnetic paints would actually produce under a magnetic field is nowadays an interesting topic still requiring further exploration. To our knowledge, no study has paid attention to the competition between magnetic interaction and polymers deposition in such paints. This is also of particular complexity because of the inherent multi-component nature of the liquid, which can lead to many surprising effects [105]. Amongst others, it has been shown that magnetic field also interact with and deteriorate regular acrylic paint [106]. Besides this, one can expect the actual deposit to depend on the exact composition of the paint, especially of the binder and the magnetic components. Indeed, previous work has shown that non-magnetic binding of the particles to the surface is a requisite to keep the magnetic structures in the evaporative deposit [90]. Some binder might then be required for an external field to have any effect, but too much binder might as well hinder the magnetic interaction, or attach the magnetic particles too strongly or too fast. Moreover, for a ferrofluid (i.e. a suspension with nanometric magnetic particles), a perpendicular magnetic field can also have the same homogenizing effect [107]. It is then of fundamental importance to understand the influence of the suspensions basic properties, such as the size and organization of magnetic particles, to actually model those more complex situations and choose relevant components for specific applications.
29To sum up, evaporating superparamagnetic colloids have then proven to be a flexible system. Indeed, their dried deposit can be remote-controlled via the external magnetic field, during the evaporation process. This system could then be adapted to produce control deposits for some applications requiring surface texturing at micrometric scale. Moreover, their versatility also makes them a good candidate as a model system to understand the fundamental mechanisms behind the deposition of colloids. The current results regarding their dried deposits are already an achievement, but they could also serve as a starting point to induce further knowledge valid on more complex but less versatile systems.
Bibliographie
[1] R. Blossey, Nature Materials 2, 301 (2003).
[2] J. Genzer and A. Marmur, MRS Bulletin 33, 742 (2008).
[3] F. Geyer et al., Science Advances 6, eaaw9727 (2020).
[4] N. Martínez, A. Rico, C. Múnez, C. Prieto, and P. Poza, Solar Energy 199, 585 (2020).
[5] D. C. Conner, A. Greenfield, P. N. Atkar, A. A. Rizzi, and H. Choset, IEEE Transactions on Automation Science and Engineering 2, 381 (2005).
[6] M. Fogliati et al., JCT research 3, 117 (2006).
[7] K. Franke and S. Rose, Ink-deposition model: The relation of writing and ink deposition processes, in Ninth International Workshop on Frontiers in Handwriting Recognition, pp. 173-178, IEEE, 2004.
[8] F. Burmeister et al., Langmuir 13, 2983 (1997).
[9] M. Wood, Journal of the Royal Society Interface 4, 1 (2006).
[10] C. D. O'Connell, M. J. Higgins, D. Marusic, S. E. Moulton, and G. G.Wallace, Langmuir 30, 2712 (2014).
[11] G. Edelman, T. G. van Leeuwen, and M. C. Aalders, Forensic science international 223, 72 (2012).
[12] M. Raymond, E. Smith, and J. Liesegang, Science and justice 36, 161 (1996).
[13] K. Sefiane, Journal of Bionic Engineering 7, S82 (2010).
[14] T. A. Yakhno et al., IEEE engineering in medicine and biology magazine 24, 96 (2005).
[15] B. S. Sikarwar, M. Roy, P. Ranjan, and A. Goyal, Journal of medical engineering & technology 40, 245 (2016).
[16] D. Brutin, B. Sobac, B. Loquet, and J. Sampol, Journal of fluid mechanics 667, 85 (2011).
[17] L. Bahmani, M. Neysari, and M. Maleki, Colloids and Surfaces A: Physicochemical and Engineering Aspects 513, 66 (2017).
[18] R. Chen, L. Zhang, D. Zang, and W. Shen, Advances in colloid and interface science 231, 1 (2016).
[19] L. Hamadeh et al., Scienti_c reports 10, 1 (2020).
[20] D. Brutin and V. Starov, Chemical Society Reviews 47, 558 (2018).
[21] S.-a. Ryu, J. Y. Kim, S. Y. Kim, and B. M. Weon, Scienti_c Reports 7, 1079 (2017).
[22] V. Vysotskii, V. Roldughin, O. Y. Uryupina, I. Senchikhin, and A. Zaitseva, Colloid Journal 79, 190 (2017).
[23] D. Brutin, B. Sobac, and C. Nicloux, J. Heat Transfer 134, 061101 (2012).
[24] H. Y. Erbil, Advances in colloid and interface science 170, 67 (2012).
[25] T. Kajiya, D. Kaneko, and M. Doi, Langmuir 24, 12369 (2008).
[26] Á. G. Marín, H. Gelderblom, D. Lohse, and J. H. Snoeijer, Phys. Fluids 23,1111 (2011).
[27] Á. G. Marín et al., Proc. Nat. Acad. Sci. U.S.A. 109, 16455 (2012).
[28] R. D. Deegan et al., Nature 389, 827 (1997).
[29] R. D. Deegan et al., Physical review E 62, 756 (2000).
[30] D. Mampallil and H. B. Eral, Advances in colloid and interface science 252, 38 (2018).
[31] P. J. Yunker, T. Still, M. A. Lohr, and A. Yodh, Nature 476, 308 (2011).
[32] H. Hu and R. G. Larson, The Journal of Physical Chemistry B 110, 7090 (2006).
[33] H. Kim et al., Physical review letters 116, 124501 (2016).
[34] R. Bennacer and K. Sefiane, Journal of Fluid Mechanics 749, 649 (2014).
[35] J. R. Christy, Y. Hamamoto, and K. Se_ane, Physical review letters 106, 205701 (2011).
[36] J. Bentley and G. P. A. Turner, Introduction to paint chemistry and principles of paint technology (CRC Press, 1997).
[37] R. Talbert, Paint technology handbook (CRC Press, 2007).
[38] A. Reuvers, Progress in Organic Coatings 35, 171 (1999).
[39] A. Overbeek, F. Bückmann, E. Martin, P. Steenwinkel, and T. Annable, Progress in organic coatings 48, 125 (2003).
[40] O. Preininger, J. Vinklárek, J. Honzí£ek, T. Mikysek, and M. Erben, Progress in Organic Coatings 88, 191 (2015).
[41] D. J. Shaw, Introduction to colloid and surface chemistry (Butterworth, 1966).
[42] T. Cosgrove, Colloid science: principles, methods and applications (John Wiley& Sons, 2010).
[43] M. Elimelech, J. Gregory, and X. Jia, Particle deposition and aggregation: measurement, modelling and simulation (Butterworth-Heinemann, 2013).
[44] D. H. Everett et al., Basic principles of colloid science (Royal society of chemistry, 2007).
[45] B. Cabane and S. Hénon, Liquides: solutions, dispersions, émulsions, gels (Belin, 2007).
[46] R. Pashley and M. Karaman, Applied colloid and surface chemistry (John Wiley & Sons, 2005).
[47] P. C. Hiemenz and R. Rajagopalan, Principles of Colloid and Surface Chemistry, revised and expanded (CRC press, 1997).
[48] R. Bhardwaj, X. Fang, P. Somasundaran, and D. Attinger, Langmuir 26, 7833 (2010).
[49] A. Darras, N. Vandewalle, and G. Lumay, Physical Review E 98, 062609 (2018).
[50] V. Soulié et al., Physical Chemistry Chemical Physics 17, 22296 (2015).
[51] G. Kuznetsov, S. Misyura, R. Volkov, and V. Morozov, Colloids and Surfaces A: Physicochemical and Engineering Aspects 572, 37 (2019).
[52] H. Hu and R. G. Larson, Langmuir 21, 3972 (2005).
[53] V. X. Nguyen and K. J. Stebe, Physical Review Letters 88, 164501 (2002).
[54] T. Still, P. J. Yunker, and A. G. Yodh, Langmuir 28, 4984 (2012).
[55] A. Marin et al., Physical review _uids 4, 041601 (2019).
[56] S. Shyam, P. Mondal, and B. Mehta, Soft Matter 16, 6619 (2020).
[57] K. J. Mutch, V. Koutsos, and P. J. Camp, Langmuir 22, 5611 (2006).
[58] Y. I. Dikanskii, A. Zakinyan, L. Khalupovskaya, V. Goncharov, and N. Demidova, Colloid Journal 81, 501 (2019).
[59] A. Darras, F. Mignolet, N. Vandewalle, and G. Lumay, Physical Review E 98, 062608 (2018).
[60] J. Faraudo and J. Camacho, Colloid Polym. Sci. 288, 207 (2010).
[61] J. H. Promislow, A. P. Gast, and M. Fermigier, J. Chem. Phys. 102, 5492 (1995).
[62] J. Faraudo, J. S. Andreu, C. Calero, and J. Camacho, Advanced Functional Materials 26, 3837 (2016).
[63] J. Faraudo, J. S. Andreu, and J. Camacho, Soft Matter 9, 6654 (2013).
[64] J. W. Tavacoli et al., Soft Matter 9, 9103 (2013).
[65] C. T. Yavuz et al., Science 314, 964 (2006).
[66] K. M. Krishnan, IEEE Trans. Magn. 46, 2523 (2010).
[67] J. L. Corchero and A. Villaverde, Trends Biotechnol. 27, 468 (2009).
[68] U. Jeong, X. Teng, Y.Wang, H. Yang, and Y. Xia, Adv. Mater. 19, 33 (2007).
[69] J. S. Andreu, J. Camacho, and J. Faraudo, Soft Matter 7, 2336 (2011).
[70] G. P. Gajula, M. T. Neves-Petersen, and S. B. Petersen, Appl. Phys. Lett. 97, 103103 (2010).
[71] K. S. Khalil et al., Nat. Commun. 3, 794 (2012).
[72] Y. Gurevich, Y. Mankov, and R. Khlebopros, Dokl. Phys. 11, 478 (2013).
[73] F. Martinez-Pedrero and P. Tierno, Phys. Rev. Applied 3, 051003 (2015).
[74] H. Carstensen, V. Kapaklis, and M. Wol_, Phys. Rev. E 92, 012303 (2015).
[75] S. S. Leong et al., Langmuir 36, 8033 (2020).
[76] T. Yang et al., Proceedings of the National Academy of Sciences 117, 18186 (2020).
[77] R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello, and B. B. Yellen, Nature 457, 999 (2009).
[78] F. Martinez-Pedrero and P. Tierno, Phys. Rev. Applied 3, 051003 (2015).
[79] P. Liu, J. W. De Folter, A. V. Petukhov, and A. P. Philipse, Soft Matter 11, 6201 (2015).
[80] A. Darras, J. Fiscina, N. Vandewalle, and G. Lumay, American Journal of Physics 85, 265 (2017).
[81] S. Fraden, A. J. Hurd, and R. B. Meyer, Phys. Rev. Lett. 63, 2373 (1989).
[82] M. Kolb, Phys. Rev. Lett. 53, 1653 (1984).
[83] F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt, and J. Callejas-Fernández, Phys. Rev. E 76, 011405 (2007).
[84] S. Miyazima, P. Meakin, and F. Family, Phys. Rev. A 36, 1421 (1987).
[85] P. Domínguez-García, J. Pastor, and M. Rubio, Eur. Phys. J. E 34, 1 (2011).
[86] A. Darras, J. Fiscina, M. Pakpour, N. Vandewalle, and G. Lumay, The European Physical Journal E 39, 47 (2016).
[87] A. Darras, E. Opsomer, N. Vandewalle, and G. Lumay, Scientific reports 7, 1 (2017).
[88] R. Messina and I. Stankovi¢, Physica A: Statistical Mechanics and its Applications 466, 10 (2017).
[89] A. Darras, E. Opsomer, N. Vandewalle, and G. Lumay, The European Physical Journal E 42, 123 (2019).
[90] A. Darras, N. Vandewalle, and G. Lumay, Colloid and Interface Science Communications 32, 100198 (2019).
[91] J. Yu, B. Wang, X. Du, Q. Wang, and L. Zhang, Nature communications 9, 3260 (2018).
[92] J. Durán, J. Arias, V. Gallardo, and A. Delgado, Journal of Pharmaceutical Sciences 97, 2948 (2008).
[93] S. Ebbens, Current opinion in colloid & interface science 21, 14 (2016).
[94] J. Katuri, X. Ma, M. M. Stanton, and S. Sánchez, Accounts of chemical research 50, 2 (2017).
[95] D. Vilela, M. M. Stanton, J. Parmar, and S. Sánchez, ACS Applied Materials & Interfaces 9, 22093 (2017).
[96] F. Mushtaq et al., Journal of Materials Chemistry A 3, 23670 (2015).
[97] I. Badge, S. P. Bhawalkar, L. Jia, and A. Dhinojwala, Soft Matter 9, 3032 (2013).
[98] G. Caputo et al., The Journal of Physical Chemistry C 112, 701 (2008).
[99] S. Utech, K. Bley, J. Aizenberg, and N. Vogel, Journal of Materials Chemistry A 4, 6853 (2016).
[100] Y. Li, G. Duan, G. Liu, and W. Cai, Chemical Society Reviews 42, 3614 (2013).
[101] X. Fang, Y. Bando, U. K. Gautam, C. Ye, and D. Golberg, Journal of materials chemistry 18, 509 (2008).
[102] S. Fan et al., Science 283, 512 (1999).
[103] M. Wood, Journal of the Royal Society Interface 4, 1 (2007).
[104] P. M. Tessier et al., Advanced Materials 13, 396 (2001).
[105] C. Diddens, J. G. Kuerten, C. Van der Geld, and H. Wijshoff, Journal of colloid and interface science 487, 426 (2017).
[106] G. Bikul'chyus, R. Butkene, and A. Ruchinskene, Protection of metals 42, 498 (2006).
[107] M. Jadav, R. Patel, and R. Mehta, Journal of Applied Physics 122, 145302 (2017).