Samuel Nicolay

Pixels, pinceaux et probabilités
De la représentation numérique à la signature stylistique des artistes

Inhoudstafel

Manuscrit reçu le 3 novembre 2025 et accepté le 4 novembre 2025

Article publié selon les termes et conditions de la licence Creative Commons CC BY 4.0.

Communication présentée au colloque annuel de la Société Royale des Sciences de Liège sur « L’art au service de la science, la science au service de l’art », Université de Liège (Belgique), 28 novembre 2025.

1. De l’image au tableau de nombres : représentations

1Pour représenter une image, l’idée la plus naturelle consiste à en coder les couleurs : chaque pixel se voit attribuer une ou plusieurs valeurs numériques décrivant son intensité lumineuse ou sa teinte. Cette approche conduit à une représentation directe de l’image sous la forme d’un tableau de nombres. Toutefois, il est d’autres façons d’encoder l’information, mathématiquement équivalentes mais relevant d’un domaine distinct ; nous y reviendrons plus avant dans la section suivante. La transformée de Fourier, par exemple, décrit l’image dans le domaine des fréquences, en exprimant son contenu en termes d’oscillations élémentaires. La transformée en ondelettes, quant à elle, s’inscrit dans le domaine des échelles : elle décompose l’image en motifs de tailles variées et de localisations précises. Dans tous les cas, qu’il s’agisse d’une description directe ou transformée, l’image se ramène toujours à un ensemble ordonné de valeurs numériques.

2Pour compresser une image, deux approches principales s’offrent à nous : la compression sans perte, qui préserve intégralement l’information, et la compression avec perte, qui accepte une altération partielle du contenu en échange d’un gain substantiel en espace de stockage. Cette dernière, bien que destructrice, permet d’atteindre des taux de compression beaucoup plus élevés, au prix d’une dégradation progressive de la qualité visuelle lorsque l’on réduit davantage la taille du fichier, c’est-à-dire la quantité de données numériques nécessaire pour stocker l’image. Les méthodes les plus performantes n’opèrent toutefois pas directement sur les intensités lumineuses des pixels, mais sur une représentation transformée de l’image, obtenue, par exemple, dans un autre domaine.

3Deux formats de compression illustrent bien cette idée : le JPEG (Joint Photographic Experts Group en anglais) et le JPEG 2000. Le premier repose sur la transformée en cosinus discrète, qui décompose l’image en motifs périodiques de différentes fréquences. Le second s’appuie sur la transformée en ondelettes discrète, capable de représenter les détails à plusieurs échelles. Si les deux formats suivent le même principe—transformer l’image avant de la compresser—leurs performances diffèrent : JPEG 2000 offre en général une meilleure qualité à taux de compression équivalent et une dégradation plus progressive lorsque la compression est forte.

4Le lecteur intéressé par l’approche présentée ici et dans le paragraphe suivant peut se référer à [1].

2. Voir le signal autrement : du temps aux échelles

5La transformée de Fourier illustre la dualité entre deux manières complémentaires de décrire un même phénomène. En musique, on peut appréhender un morceau soit comme une succession de sons dans le temps—une mélodie que l’on écoute ou que l’on lit sur une portée—soit comme une combinaison de fréquences correspondant aux notes qui le composent. La première description met en évidence le déroulement temporel, la seconde révèle la structure harmonique. De même, la transformée de Fourier permet de passer d’une représentation temporelle d’un signal (son évolution au fil du temps) à une représentation fréquentielle (sa décomposition en composantes sinusoïdales). Le principal inconvénient de la représentation fréquentielle pure est qu’elle perd toute information temporelle : on connaît les fréquences présentes dans le signal, mais on ignore quand elles apparaissent. Pour remédier à cette limitation, on peut analyser le signal dans des fenêtres temporelles successives, en effectuant une transformée de Fourier sur chacune d’elles. Cette approche, appelée transformée de Fourier à court terme, permet de suivre l’évolution des composantes fréquentielles au fil du temps, mais au prix d’un compromis entre résolution temporelle et résolution fréquentielle. La transformée en ondelettes s’inscrit dans cette continuité en raffinant le principe : elle adapte la taille de la fenêtre à la fréquence étudiée, large pour les basses fréquences (qui évoluent lentement) et étroite pour les hautes fréquences (plus brèves et localisées). La décomposition repose sur le choix d’une ondelette de base, dont les dilatations et translations servent à représenter le signal. Ce procédé confère une flexibilité bien plus grande dans l’analyse des signaux dont les caractéristiques changent au cours du temps.

6Ainsi, un signal f peut être décomposé en une somme d’ondelettes, chacune localisée à la fois dans le temps et dans la fréquence. Dans le cadre des ondelettes discrètes, cette décomposition s’écrit :

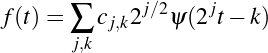
7où ψ est l’ondelette de base et c_j,k sont les coefficients d’ondelettes associés aux différentes échelles j et positions k. Chaque coefficient c_j,k mesure la contribution de l’ondelette correspondante à la reconstruction du signal. Cette double dépendance permet de représenter finement les variations locales du signal, tant du point de vue de sa structure temporelle que de son contenu spectral. La décomposition obtenue dépend bien sûr du choix de l’ondelette de base ψ, mais les propriétés essentielles, notamment la capacité à restituer fidèlement l’information du signal, sont largement indépendantes de ce choix.

8De cette manière, un signal peut être associé à une suite de nombres représentant ses coefficients d’ondelettes ; cette suite constitue alors une représentation alternative du signal initial. En analyse, il est courant de regrouper les fonctions présentant des propriétés similaires au sein d’espaces fonctionnels, tels que l’espace des fonctions continûment dérivables ou celui des fonctions mesurables à carré intégrable. Or, ces propriétés se traduisent souvent directement dans la structure des coefficients d’ondelettes : par exemple, la régularité (au sens de Hölder) d’une fonction se manifeste par une décroissance rapide de ses coefficients aux petites échelles, c’est-à-dire pour les hautes fréquences de la décomposition. Ainsi, un espace fonctionnel peut être interprété comme un espace de suites de nombres satisfaisant certaines conditions précises, offrant une passerelle élégante entre l’étude des fonctions et celle de leurs représentations discrètes.

3. Capturer le style d’un artiste à l’aide des ondelettes

9Nous résumons ici l’essentiel des travaux présentés dans [2] et [3].

10Plutôt que d’analyser directement les teintes ou les textures visibles d’une image pour en extraire une signature stylistique d’un artiste, on peut étudier la structure plus profonde révélée par sa décomposition en ondelettes. Les coefficients ainsi obtenus traduisent les variations locales de l’image à différentes échelles, et leur organisation recèle des motifs caractéristiques du geste ou de la technique picturale. Ces coefficients présentent toutefois des propriétés particulières : ils sont corrélés entre eux, notamment à travers les échelles voisines, et leur distribution est généralement non gaussienne, marquée par la présence de valeurs extrêmes rares mais significatives.

11Pour modéliser ces dépendances, les « arbres de Markov cachés » (HMT, hidden Markov trees en anglais) constituent un outil statistique particulièrement adapté [4]. Dans ce cadre, chaque coefficient d’ondelette est associé à un état latent qui capture sa « significativité » (forte ou faible amplitude). Les états latents suivent une structure arborescente reflétant la hiérarchie des échelles  le coefficient à une échelle donnée dépend probabilistiquement de l’état de son parent à l’échelle supérieure. Ce modèle permet de capturer à la fois la corrélation inter-échelles et la nature non gaussienne des coefficients, offrant une représentation compacte et efficace de la structure statistique de l’image. L’estimation des paramètres du HMT à partir des coefficients d’ondelettes permet ainsi de décrire et comparer les motifs caractéristiques d’un artiste de manière quantitative.

12Ces structures statistiques, issues de l’analyse en HMT des coefficients d’ondelettes, peuvent être interprétées comme une signature numérique de l’artiste, reflétant son style propre de manière objective et reproductible. Les méthodes basées sur ces modèles ont le potentiel d’assister les experts dans la détection de contrefaçons, en identifiant des écarts subtils par rapport aux motifs statistiques attendus. Au-delà de l’authentification, elles offrent également un outil pour quantifier les différences stylistiques perçues intuitivement par les historiens de l’art, permettant de comparer les œuvres entre elles selon des critères mesurables et rigoureux.

13Dans le Polyptyque Peruzzi de Giotto (Fig. 1), Saint François se distingue des autres figures par une modélisation plus sculpturale et des contours plus affirmés, conférant au personnage une présence plus expressive. Ces différences stylistiques, contrastant avec la douceur et la planéité des autres saints, peuvent refléter un accent délibéré sur ce personnage central ou la participation de différents assistants dans l’atelier (notamment Stefano Fiorentino), soulignant ainsi sa singularité au sein du polyptyque. L’analyse en ondelettes, couplée à un modèle HMT, confirme que ce panneau est stylistiquement distinct des autres [2].

Figure 1: Le polyptyque Peruzzi est un retable peint a tempera sur fond d’or sur panneau de bois de Giotto di Bondone, daté vers 1318–1322. Les personnages représentés sont, dans l’ordre : saint Jean l’Évangéliste, la Vierge, le Rédempteur, saint Jean-Baptiste et saint François. Source : Wikimedia Commons (consulté le 3 novembre 2025).

14Une autre approche de l’analyse d’une peinture repose sur les espaces fonctionnels. Si l’on considère l’image comme une fonction définie sur le plan, il est possible d’étudier sa régularité en chaque point (x,y). Cette régularité locale se quantifie par un nombre positif, appelé exposant de Hölder, qui mesure la finesse ou la singularité du signal à ce point [1]. Pour passer d’une vision locale à une vision globale, on considère la distribution de ces exposants à travers l’ensemble de l’image : le spectre multifractal associe à chaque exposant sa « taille », souvent exprimée via la dimension de Hausdorff des points correspondants. Une peinture peut ainsi être représentée par un spectre reflétant la répartition des irrégularités et textures du tableau, offrant une signature globale de sa structure visuelle. Les peintures peuvent ensuite être comparées entre elles via leur spectre multifractal, fournissant une mesure quantitative des irrégularités propres à chaque œuvre.

15Cette méthode a été appliquée à des tableaux de Van Gogh, mélangés avec d’autres artistes, afin de distinguer les œuvres authentiques de celles qui ne le sont pas. Deux critères ont été retenus pour classer les peintures : l’exposant de Hölder minimum du spectre et un critère lié à la convexité du spectre (le coefficient de linéarité de sa transformée de Legendre). L’approche a donné des résultats très satisfaisants, confirmant son efficacité pour détecter des signatures stylistiques propres à l’artiste.

Informations supplémentaires

Identifiant ORCID de l’auteur

160000-0003-0549-0566 (Samuel Nicolay)

Conflits d’intérêt

17L’auteur déclare l’absence de tout conflit d’intérêt.

Bibliographie

Om dit artikel te citeren:

Over : Samuel Nicolay