- Portada
- Volume 88 - Année 2019
- Articles
- Réciprocité
Vista(s): 1655 (28 ULiège)
Descargar(s): 539 (0 ULiège)
Documento adjunto(s)
Version PDF originaleRésumé
On présente une généralisation du principe de réciprocité de Maxwell pour pouvoir l’utiliser même avec des conditions différentes d´appuis.
Abstract
It is a generalization of the principle of reciprocity of Maxwell to use it even with different support conditions.
I Prolégomènes
1Hommage à mon père
2 Beaucoup d´ingénieurs encore en activité, proches de la pension, ou déjà pensionnés, ont eu l´occasion d´écouter les cours faits par mon père, Albert Pirard, à l’ULg. et d´étudier dans ses notes rédigées très clairement. Il faut reconnaître que ses notes de cours étaient diversifiées, didactiques et très compréhensibles.
3 Dans chacun de ses cours, il a réussi à mettre un apport personnel qui produisait une avance dans la matière en question.
4 Encore maintenant, d’anciens étudiants me demandent la possibilité d´obtenir tel ou tel de ses cours. Mon père n´a jamais réalisé son enseignement sans publier les notes correspondantes : Mécanique (3 tomes), Grafostatique (1 tome), Géométrie descriptive (2 tomes), Hyperstatique (1 tome), Élasticité (1 tome), Photoélasticité (1 tome). Sans entrer dans la liste de ses nombreuses publications (Holographie, Moiré, etc.).
5 Curieusement, il en va dans l´enseignement un peu comme dans l´évolution des civilisations. L´apogée d´une civilisation, marque le début de sa fin ; ou le début de sa fin, marque l´apogée.
6 Évidemment l´enseignement doit évoluer et mon père le savait très bien. En Graphostatique (Science introductive à l´art de construire), il a fait évoluer cette science par plusieurs généralisations jusqu´à son apogée qui fut la résolution du problème le plus difficile de cette matière, en se basant sur la Méthode de Mayor, la décomposition graphique d´une force de l´espace en six directions données (ce qui n’avait jamais été fait auparavant). Mais cette apogée fut aussi la fin de cette matière si formatrice, évincée par les calculs automatiques des ordinateurs. Ces derniers travaillent très vite mais ne forment pas dans la discipline des statiques.
7 Le traité d´hyperstatique analytique et graphique arrive aussi à son apogée par la généralisation du principe de Maxwell que nous allons voir ci-dessous. Ce dernier ouvre la porte au changement de système isostatique fondamental pour chaque inconnue hyperstatique. Les ordinateurs se sont chargés aussi d´évincer cette matière. Mon père voyait très bien ce qui arrivait avec les ordinateurs, mais il a réussi à maintenir l´aspect formatif de ces matières et de ses notes de cours.
8 La même chose s’est passée avec la géométrie descriptive. Cette branche si formative a disparu de l´enseignement, remplacée par des programmes de dessins automatisés.
9 Ne me faites pas dire ce que je n´ai pas dit. Les transformations des méthodes de calculs par les ordinateurs doivent être incorporées à l´enseignement, évidemment. Mais s´il est indubitable que l´utilisation de l´ordinateur dans les bureaux d´études est fondamental, l´enseignement en général n´a pas encore trouvé son équilibre entre la formation et l´information.
10 Pourquoi apprendre à dériver et intégrer des fonctions, demandent les étudiants ? À notre époque nous avons fait des dizaines ou centaines d´exercices de dérivations et d´intégrations. Et cela nous a formés aux calculs algébriques. Mais, maintenant, les étudiants nous disent : Pourquoi tant d´exercices si les programmes d’ordinateur dérivent ou intègrent analytiquement ? Et c´est vrai. Et nous pouvons remonter jusqu´en primaires : Pourquoi, dès lors, apprendre de mémoire les tables de multiplications si nous les avons en poche ?
11 La révolution de l´enseignement est en marche, mais l´adaptation des enseignants est plus lente que l´évolution des ordinateurs. C´est quelquefois assez désespérant de laisser tomber des matières que l´on juge formatives, et qui le sont, pour les remplacer par des touches d´ordinateur.
12 En effet, si l´on considère que les tables de multiplications sont importantes pour former la mémoire de l´enfant, il faudra trouver autre chose pour cette formation.
13 Et si les exercices de dérivées et d´intégrales ont perdu leurs sens, il faudra en inventer d´autres qui obligeront les étudiants à penser profondément au sens original de ces opérations. Par exemple, proposer des exercices où, en plus d´établir une certaine fonction, l´étudiant doit décider s’il doit intégrer ou dériver cette fonction pour obtenir la solution du problème proposé. Penser et préparer ce genre d’exercices n´est pas facile.
14 Notre génération a reçu une solide formation de base qui nous a permis de nous adapter le mieux possible aux évolutions. Mais nous restons un peu pensifs face aux nouvelles générations dont nous sommes responsables de la formation, et comme dit plus haut, que l´on informe plus que l’on ne forme. (C´est l´ère de l’informatique.)
15 Tous les enseignants ont dû s´adapter au temps où ils vivaient, mais notre époque est assez secouée de ce point de vue.
16 Revenons à nos moutons.
17 Mon père a été de son époque. Il a formé, et bien formé, plusieurs générations d´ingénieurs, qui, d´habitude et selon ce qu´on me raconte, lui en sont reconnaissantes.
Je reprends ici ce qu´il a écrit lui-même : «J’ai été de mon temps. Je considère aussi que je suis parti à temps. L’actualité n’est plus à la statique, ni à la mécanique analytique, ni à l’hyperstatique ni à la photoélasticité, ni à la géométrie ni au dessin.
C’est à l’ordinateur que l’on confie ces besognes matérielles, et peut-être le soin d’enseigner la philosophie à nos successeurs.»
18 Une des apogées dont je parlais ici plus haut est sans nul doute la généralisation du Principe de Réciprocité de Maxwell. Je ne l´ai vue nulle part ailleurs que dans le cours de mon père, et je la présente ci-dessous, non en copiage, mais avec une démonstration un peu différente.
II. Article
19 On peut se demander: que peut-on dire sur la réciprocité dans le calcul des structures qui n´a pas déjà été dit ou écrit? Très peu en vérité. On pourrait même dire, presque rien dans son aspect pratique. Par conséquent, les considérations que nous faisons ici sont essentiellement théoriques. La première apparition de la réciprocité est due à Maxwell en 1864. La simplicité de l’énoncé et de la démonstration basée sur des arguments énergétiques est notable. Il semblerait que Maxwell «eut besoin» de ce théorème. Il l´a énoncé en deux lignes, démontré en deux autres et a continué à travailler. Il ne mentionne pas le terme de réciprocité et probablement n’a pas réalisé l’importance de ce qu´il avait écrit et démontré, parce que la notion de ligne influence n’existait même pas et la notion de matrice de rigidité non plus.
20 Dans notre cas, l´énoncé de Maxwell est très simple :
21 Si une cause agit en un point A d´un corps élastique, la déformation qui se produit en un autre point B du système est égale à celle qui se produit en A si la cause agit en B.
22 Selon Maxwell la charge P (cause) agissant en A, produit vB en B, et la même charge P agissant en B produit en A vA et donc, Fig. 1 a y b.
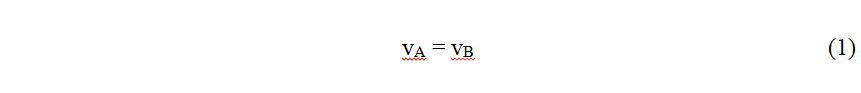

23 Il est clair que comme cause et déformation on peut considérer, comme ici, P et v, ou Couple, C et rotation .
24 Si, sur un corps nous avons une force P et, sur l’autre, une force Q, nous avons la situation de Fig. 2 a et b. La démonstration de Maxwell basée sur travail et énergie nous donne :
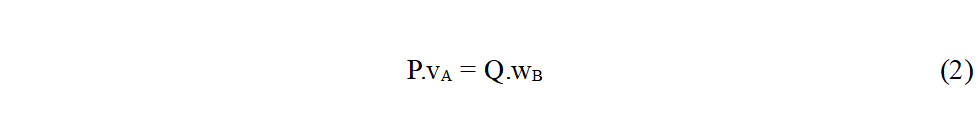

25 Nous voyons bien ainsi que la réciprocité n’est pas dans les déplacements mais dans les travaux. Nous pouvons énoncer :
26 Le travail de P durant les déplacements produits par Q est égal au travail Q pendant les déplacements produits par P.
27 En 1872 est venue la généralisation de Betti. Il considère un état de charges avec plusieurs forces P, soit Pi et un autre état de charges avec plusieurs forces Q soit Qj. Avec des raisonnements semblables à ceux de Maxwell, soit par des considérations énergétiques, il est établi que :
28 Les travaux réalisés par un état de charges 1 pendant les déplacements produits par un état des charges 2 est égal aux travaux de l´état de charges 2 pendant les déplacements produits par l’état de charges 1.
29Soit ici :
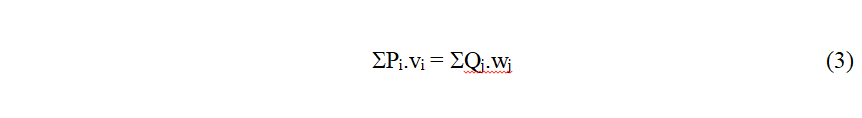
30De nouveau les charges P et Q pourraient être des couples.
31 L´utilisation pratique se fait habituellement avec un état de charges 2 qui contient une seule force unité en un point B et on obtient wB, le déplacement en B, produit par l’état de charges 1.
32 La généralisation suivante se trouve dans le cours de mon père «Traité d´hyperstatique analytique et graphique»1. Dans ce cours, il introduit le changement de référence, soit d’appuis, entre l’état de charges 1 et l´état de charges 2. La démonstration, qui ne laisse aucun doute, est basée sur la réciprocité de Maxwell, l’utilisation de la règle de Vereschaguin, dite règle de S. Y., pour l’intégrale du produit de deux fonctions linéaires et sur l’utilisation du théorème des travaux virtuels. Ici nous allons développer une démonstration différente.
33 Pour simplifier, nous travaillerons sur des poutres élastiques chargées perpendiculairement à la fibre moyenne. Soit des charges réparties p(x), soit concentrées Pi ou des couples Cj. Pour le travail de ces charges on utilisera, selon le cas, une des expressions suivantes, équivalentes pour nous.
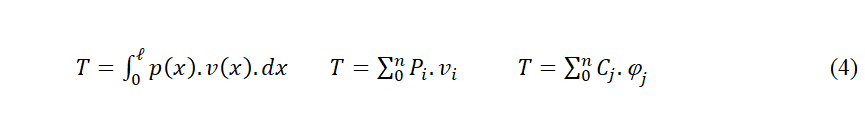
34 Le seul outil mathématique que nous utiliserons est la première règle d’intégration ou l’intégration par partie.
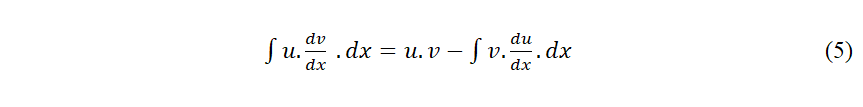
35 À partir de ces expressions, simples et bien connues, nous arriverons à des expressions pratiques très importantes.
36 Tout d’abord, nous considérerons que u est la dérivée d´une certaine fonction w, alors l’expression ci-dessus sera :
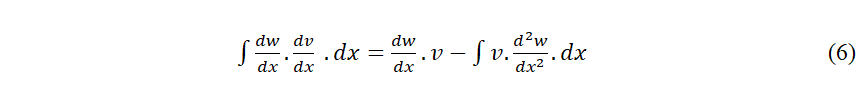
37 L´expression de gauche est parfaitement symétrique en “v” et “w”. Par conséquent, dans le membre de droite, on peut invertir aussi v et w sans changer le résultat.
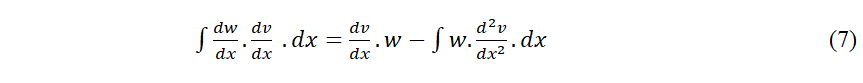
38 Et en réunissant le tout :
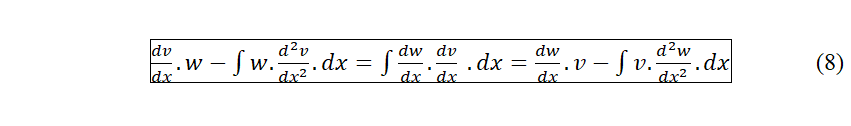
39 C’est ce qu’on pourrait appeler le Principe de Réciprocité de premier ordre entre deux fonctions «v» et «w».
40Remarque : L´utilisation doit tenir en compte les constantes d’intégration qui égalisent les trois membres pour une même valeur de x.
41 Si on applique le principe de manière définie entre “a” y “b” :
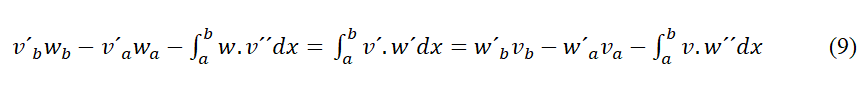
42 Ici les constantes d´intégration n´interviennent plus.
43 Comme exemple d’application, on peut dire que: pour trouver la meilleure forme de variation de l’inertie d’une colonne afin de maximiser la charge de flambage, on a utilisé cette réciprocité de premier ordre2.
44 Continuons un peu plus avec ce thème de la réciprocité. Si dans cette relation de premier ordre, nous remplaçons chaque fonction par sa dérivée, nous obtenons :
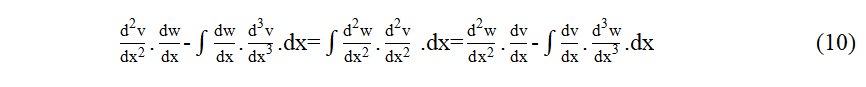
45 Et avec une intégration par partie dans le premier et troisième membre, nous obtenons le Principe de Réciprocité de second ordre :
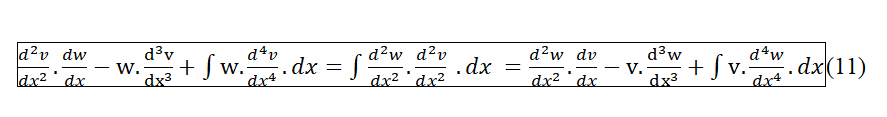
46Remarque : De nouveau, pour l´utilisation, il faut tenir compte des constantes d´intégration qui égalisent les trois membres pour une même valeur de x.
47 Si nous appliquons ce dernier principe de manière définie entre “a” y “b” :
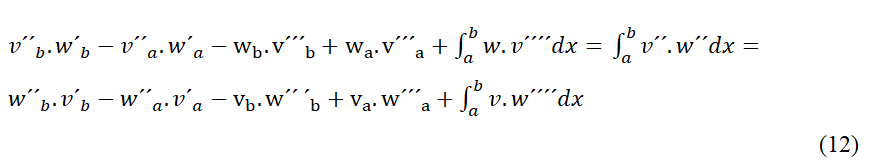
48 Ici les constantes d´intégration n´ont pas d´importance.
49 On pourrait généraliser cela à des Principes de n´importe quel ordre…
50 Il est important de comprendre la simplicité dans l’obtention de ces relations de réciprocité et de l’importance de l´utilisation. Toutes les bases du calcul des structures se trouvent dans cette relation: le théorème de Castigliano, de Menabrea, la réciprocité de Maxwell, Betti, etc., la conservation de l’énergie si nous faisons auto-réciprocité, la relation des travaux virtuels, etc. Tous dépendent de cette relation. Mais ce n’est pas parce que toutes les méthodes de calcul peuvent être basées sur cette relation de réciprocité, que l´on doit toujours l’utiliser. Dans certains cas, des méthodes moins générales et plus appropriées peuvent être plus pratiques.
51 Maintenant, regardons la mise en œuvre de ces expressions mathématiques pour le calcul des structures.
52 Nous considérons la déformation d’une poutre en flexion. Appelons v(x) l’élastique et M(x) le moment de flexion ; l’équation différentielle de l’élastique est : [basée sur la courbure, en supposant les déformations petites, en utilisant un matériau avec un comportement linéaire (Loi de Hooke), avec la rigidité de la poutre en flexion EI constante, (module E: d´élasticité du matériau, I l’inertie de la section de la poutre)]
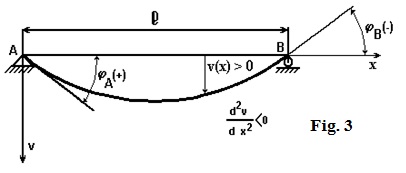
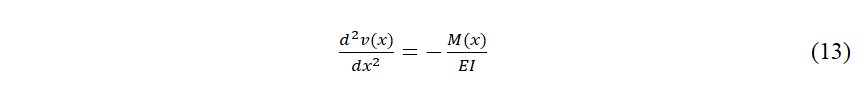
53 Le signe dépend des conventions de signe pour v(x) et pour M(x). Ici, comme indiqué sur la fig. 3, M(x) est positif quand les fibres inférieures sont en traction, et v(x) se considère positif vers le bas.
54 Nous avons ainsi les expressions différentielles connues par la statique :
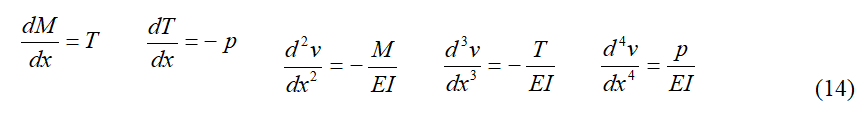
55Et à partir de l´élastique (EI constant) :
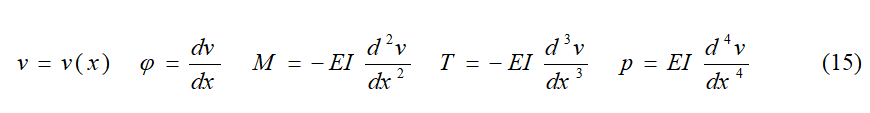
56 Nous devons insister ici sur quelque chose d´élémentaire, simple mais très important.
57 Pour obtenir le diagramme des moments ou ses expressions analytiques, un schéma libre s’effectue tout d’abord. Les inconnues de réactions sont calculées et se transforment en forces extérieures pour avoir une mise en charge équilibrée avec toutes les forces agissant de façon directe ou réactive. Mais pour les expressions analytiques du moment de flexion, ce sont toutes des forces ou des couples. Il n’y a aucune différence entre une force extérieure appliquée ou une force de réaction. En d’autres termes : le moment de flexion «ne connaît pas ses réactions» (l´effort tranchant non plus).
58 Comme dans l´équation différentielle de l’élastique intervient le moment de flexion, l´intégration donnera une expression, dans une certaine mesure, indépendante des appuis. C´est seulement quand on veut évaluer les constantes d’intégration (A, B), de forme linéaire «Ax + B», que les conditions d´appuis interviennent.
59 Nous devons ainsi nous rendre compte que les expressions mathématiques, où interviennent seulement les moments, ne dépendront pas des conditions d´appuis. Par exemple, la dérivée du moment donne l´effort tranchant qui ne dépend pas des appuis.
60 Encore une fois, il faut insister: le moment et le tranchant ne dépendent pas des appuis dans la mesure où ce sont des restrictions de déplacement; les forces de réactions introduites par les appuis doivent évidemment être prises en compte, mais apparaissent seulement comme des forces extérieures appliquées à la poutre.
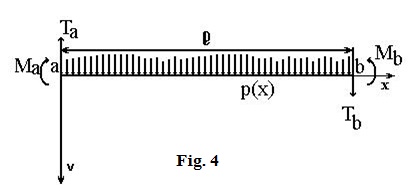
61Pour faciliter les raisonnements ci-après, appelons p(x) la charge sur une poutre et sa longueur (Fig. 4). Cette expression inclût pour nous les charges concentrées, les couples agissant sur la poutre ainsi que les réactions extériorisées. Nous devons aussi tenir en compte, à l´extrémité gauche (a), l´action de Ma y Ta et à l´extrémité droite (b) l´action de Mb y Tb ; ce sont des actions extérieures ou des réactions extériorisées. Comme le système est en équilibre, on peut écrire les équations d’équilibre statique :
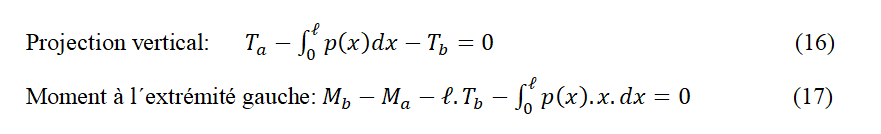
62 Si, dans cette deuxième équation, nous remplaçons Tb par sa valeur tirée de (16), nous obtenons l’équation d’équilibre relative à l’extrémité droite.
63 Nous pouvons maintenant aborder la réciprocité et envisager une même poutre, c'est-à-dire même EI, chargée différemment, l’état de charge 1, p(x), et l´état de charge 2, q(x). Les appuis sont les mêmes ou différents, mais les réactions sont supposées calculées et extériorisées, et les états de charge sont équilibrés.
64 Le premier
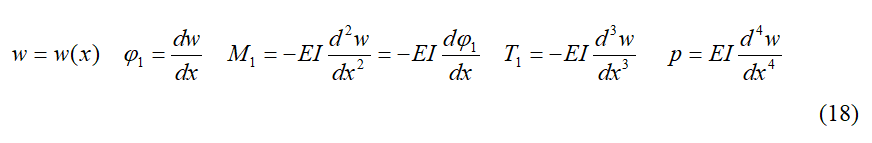
65À l´extrémité gauche wa φ1a M1a T1a
66et à l´extrémité droite wb φ1b M1b T1b
67 Le second
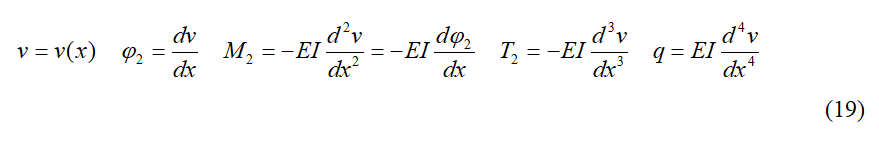
68À l´extrémité gauche M2a T2a va φ2a
69et à l´extrémité droite vb φ2b M2b T2b
70En appliquant le principe de réciprocité de second ordre que nous réécrivons ici :
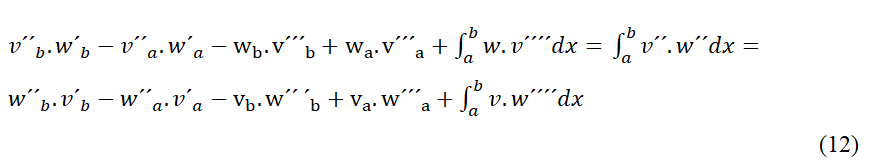
71On obtient:
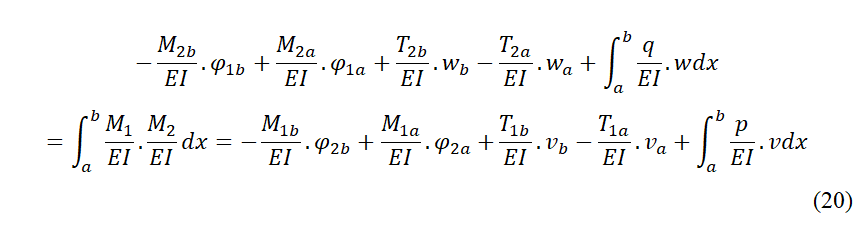
72En multipliant tout par EI, nous obtenons la Relation de Réciprocité :
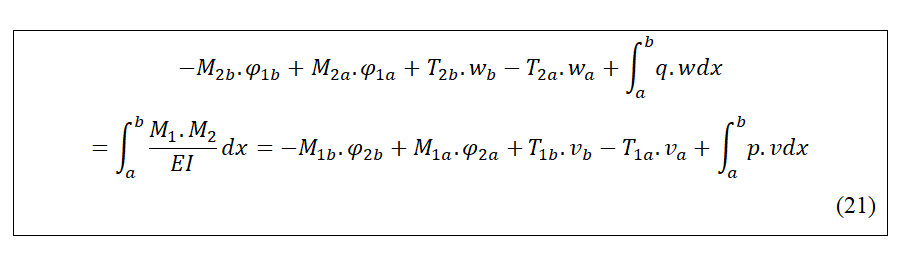
73 Cette Relation de Réciprocité établie, ici pour les poutres, est générale, réelle, utile, et permet de nombreuses conclusions.
74 Si nous analysons les deux systèmes de charge nous constatons que l’expression ci-dessus signifie que: «Le travail du système de charges 2, durant les déplacements produits par le système de charges 1 (premier terme), est égal au travail du système de charges 1 pendant les déplacements produits par le système de charges 2 (troisième terme). Les deux sont égaux à l’intégrale du centre (second terme)». La notion de réciprocité est bien explicite.
75 Comme le second terme dépend seulement des moments, le résultat est indépendant des conditions d´appuis. Cela peut sembler curieux vu que le premier et le troisième terme représentent des travaux effectués au cours d’un déplacement élastique qui dépend des appuis. Il semblerait logique que le résultat aussi dépende des appuis. Mais non, les appuis n´ont pas d´influence. Nous insistons. Quelles que soient les conditions d´appuis du premier état de charges et du deuxième, égales ou différentes, les trois membres de l’équation ci-dessus donneront des résultats numériquement égaux.
76 Nous avons un cas particulier important quand l’état de charge 1 coïncide avec le 2 et les appuis aussi. L’équation se réduit à :
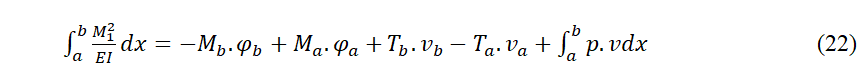
77 Si nous mettons ½ à chaque terme, nous obtenons la conservation de l’énergie: l´énergie interne de flexion est égale au Travail des charges extérieures. (Dans ce cas les réactions ne travaillent pas.)
78 Le coefficient ½ pourrait s´ajouter à chaque terme de la réciprocité mais ce n´est pas nécessaire.
79 Le terme central de la relation peut s´interpréter de deux manières réciproques aussi:
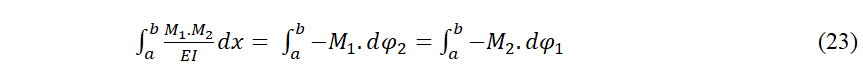
80 C´est alors le travail interne des moments produits par le système de charges 1, durant les rotations des sections produites par le système de charges 2 et vice-versa.
81 En fait, tous les grands théorèmes d’analyse structurale, auxquels sont liés de grands noms, peuvent se retrouver à partir de la réciprocité analysée ici. Avant de continuer d´analyser cette réciprocité, nous allons discuter plus en détail l’influence des conditions d´appuis.
82 Comme nous l’avons déjà souligné, les états de charge sont équilibrés. Changer les conditions d´appuis, sans changer l’état de charge, signifie tout simplement changer les constantes d’intégration A et B qui apparaissent sous la forme Ax + B. Cela représente simplement un mouvement de la poutre, déjà courbé par flexion, comme un corps rigide. Cependant, comme le système de charge est équilibré, il n´y a pas de travail qui se produit au cours de ce changement. En d’autres termes, quelles que soient les constantes d´intégration pour l’élastique de chaque poutre, les trois membres seront égaux.
83 Supposons maintenant que le second état de charge se réduise à une seule charge Q1 au point 1. Quelles que soit les conditions d´appuis choisies, mais identiques pour les deux états, le premier avec une charge p (x),
84 l’équation de réciprocité sera :
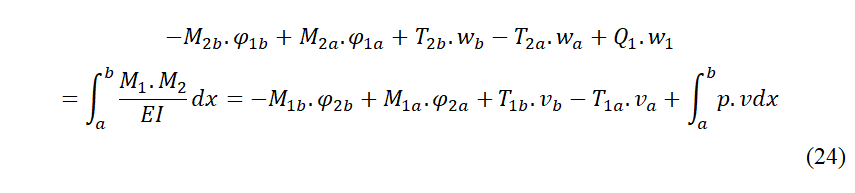
85Analysons les conditions d´appuis possibles :
1) Une articulation y un appui simple. Cela annule l´élastique en deux points. Si ce sont les extrêmes a et b de la poutre, wb = wa = M2b = M2a = 0, et si ce sont deux autres points, M2b = M2a = T2b = T2a = 0, le premier membre se réduit à Q1.w1. (Le troisième se réduit à l´intégrale.)
2) Un encastrement en a : φ1a = wa = T2b = M2b = 0 et de nouveau le premier membre se réduit à Q1.w1. Si l´encastrement est en b le résultat est le même. (De nouveau le troisième membre se réduit à l´intégrale.)
La réciprocité sera :
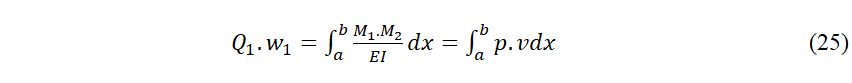
86 Le troisième membre ne s´utilise pas habituellement. Nous obtenons l’expression bien connue qui, avec Q1 unitaire, permet d’obtenir le déplacement vertical du point 1 de la première poutre, produit par les charges p(x). M1 est le moment flector produit par la charge p(x) et M2 est le moment flector produit par Q1 unitaire. Évidemment, il n’est pas nécessaire de considérer deux poutres dans ce cas ; c´est la même poutre chargée une fois avec p(x) pour obtenir M1 et ensuite la même poutre chargée avec Q1 pour M2.
87 A partir de ces expressions, on obtient facilement le Théorème de Castigliano et celui de Menabrea. Mais aussi la Règle de Vereschagin généralisée par A. Pirard et appelée la méthode des SY.
88 Si, sur la première poutre, nous avons aussi une seule force P2 en un point 2, la réciprocité sera :
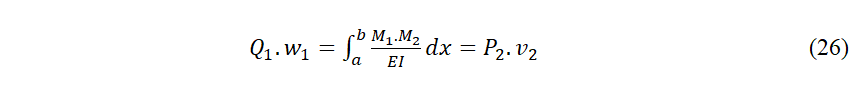
89 C´est le Principe de Réciprocité de Maxwell. Le travail de Q1, durant les déplacements produits par P2, est égal au travail de P2 durant les déplacements produits par Q1.
90 Nous allons insister un peu plus sur ce Principe de Maxwell. Habituellement ce principe se démontre à partir de considérations énergétiques très simples. L’élégance et la simplicité de la présentation faite par Maxwell est notable.
91 Pour faciliter la présentation nous allons utiliser la notation avec deux indices inférieurs :
92Vij déplacement du point i d´une poutre dû à une force P situé au point j. Comme ce déplacement est proportionnel à l´action P on peut écrire :
93Vij = P.vij vij est le déplacement en i dû à une forcé unitaire au point j.
94 Soit donc une poutre avec ses conditions d´appuis. Pour une première étape, si en un point 1 nous avons une force P, en ce même point nous avons le déplacement :
95V11 = P.v11 et au point 2 nous aurons le déplacement V21 = P.v21. Pour la seconde étape, si au point 2 nous avons la force Q, en ce même point 2 nous aurons V22 = Q.v22 et au point 1, V12 = Q.v12.
96Par application du Principe de Maxwell vu ici au-dessus,
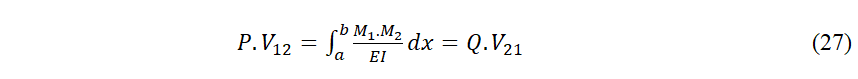
97 Soit, le travail de P, à cause des déplacements produits par Q, est égal au travail produit par Q durant les déplacements produits par P.
98Si nous utilisons les déplacements produits par des forces unitaires :
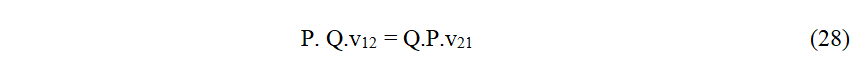
99soit

100 «Dans une poutre, le déplacement en 1, dû à une force unitaire en 2, est égal au déplacement en 2 dû à une force unitaire en 1”. C´est la forme la plus simple, élémentaire et utile du Principe de Maxwell. Les «m» sont dus à une force unique et unitaire.» (Forces et déplacements se mesurent dans la même direction.)
101 La notion de force et déplacement doit s´entendre au sens large, c.à.d. que cela peut être couple et rotation.
102 La présentation faite par Maxwell est le fondement de la théorie des lignes d’influence dans les systèmes hyperstatiques. Pour une utilisation dans les systèmes isostatiques, elle a besoin d’une petite modification dans la présentation.
103 Revenons sur la relation de Réciprocité.
104 Nous allons voir comment on peut exprimer la relation de Réciprocité en utilisant seulement les charges extérieures des états de charge, sans qu´il soit nécessaire d’extérioriser les réactions.
105 L’intégration de l’équation différentielle d’une élastique a besoin de l’évaluation des deux constantes d’intégration (A, B) qui apparaissent dans une expression linéaire, Ax + B. C´est donc une ligne droite appelée ligne de fermeture ou ligne de référence. Au temps passé, mais pas si lointain, l’élastique s´obtenait par méthodes graphiques (funiculaires) et la ligne de fermeture était obtenue en fermant le funiculaire solution par une ligne, dite de fermeture, qui annulait les flèches sur les points d’appuis par exemple. L´élastique proprement dite se mesurait entre la ligne de référence ou de fermeture et la courbe d’intégration. Dans les méthodes analytiques, la ligne de référence est généralement horizontale.
106 Dans la relation de réciprocité, comme nous l’avons déjà dit, nous pouvons dans les deux états de charge considérés et donc dans les deux élastiques obtenues, mettre la ligne de référence où nous voulons. Cela n’a aucune influence et nous pouvons «inventer» une myriade de lignes de références. Elles sont toutes valables. Il n’y a aucun intérêt à mettre la ligne de référence dans n´importe quelle position, mais il y a deux positions logiques et privilégiées. Tout d’abord, on peut mettre la ligne de fermeture correspondant à un état de charge à son emplacement normal, c'est-à-dire, compte tenu des appuis qui furent extériorisés et inclus dans l´état de charge. Ce qui est habituellement fait parce que, dans ce cas, seules les charges extérieures réalisent un travail et pas les réactions. Mais comme nous allons évaluer les travaux croisés, c'est-à-dire les charges du second état de charges avec les déplacements du premier état de charges, on peut localiser la ligne de fermeture de la première élastique en concordance avec les appuis du second état de charges. De cette manière, les réactions du second état de charges ne travailleront pas et seules les charges réellement extérieures travailleront.
107De la même façon, la ligne de fermeture du second état de charge se fera en concordance avec les appuis du premier état de charge et ainsi les réactions ne travailleront pas non plus.
108 L’expression analytique de la Relation de Réciprocité ne change en rien. La valeur de chaque membre non plus. Seulement que, maintenant, pour l’évaluation des travaux croisés, on devra prendre en compte uniquement les charges externes et pas les réactions.
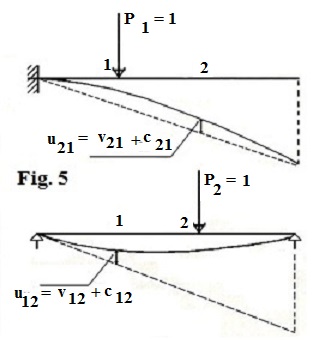
109 Si l'on considère le premier état de charge (P1) et son élastique, nous avons deux lignes possibles de fermeture. La première correspond à ses appuis propres, ici un encastrement, qui détermine par la tangente à l´élastique à l´origine, la ligne de fermeture, ici horizontale. La seconde, en pointillé, correspond aux appuis du second état de charge et annule les déplacements aux extrémités. Ces deux droites séparées donnent par la distance verticale entre elles, la Fonction Linéaire de Concordance à l’état 2 de l´état 1, C21(x). De la même manière dans l´état de charge 2 (P2), nous avons deux lignes de fermeture, celle qui lui correspond, horizontale ici, et qui annule les déplacements aux extrémités, et l´autre en concordance avec les appuis du premier état de charge, qui est la tangente à l´élastique à gauche. La distance verticale entre les deux est la fonction linéaire de concordance à l’état 1 de l´état 2, C12(x). Fig. 5.
110 Pour le travail de P1, le déplacement dans l´état 2 entre la ligne de fermeture pointillée et l´élastique doit être tenu en compte, u21 = v21 + c21. Et pour le travail de P2, le déplacement dans l´état 1 entre la ligne de fermeture pointillée et l´élastique doit être tenu en compte, u12 = v21 + c21. Donc, finalement, avec les lignes de fermetures adéquates, seules les charges extérieures directement appliquées doivent intervenir.
111 Notons que le passage d´une ligne de fermeture à une autre produit simplement un travail durant une translation, et une rotation d´un système de forces en équilibre dont le bilan est nul. Les fonctions de concordance C(x) sont de la forme (α + θ.x) soit une translation de α et une rotation de θ.
112 La relation de réciprocité de Maxwell, avec une seule charge dans chaque état et des appuis différents, sera :
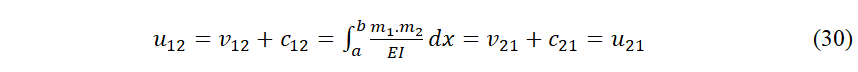
113Donc les fonctions de concordance apparaissent dans la réciprocité (seulement si les appuis sont concordants, soit les mêmes, les c sont nuls).
114u est l´élastique concordée. Ver Fig. 5.
115 Le travail d’une charge unitaire agissant au point 1 d´une poutre pendant les déplacements, produits par une charge unitaire placée au point 2, et concordés aux appuis du premier état de charge, est égal au travail accompli par la charge unitaire 2, pendant les déplacements produits par une charge unitaire placée au point 1, et concordés aux appuis du second état de charge.
116C´est le Principe de Réciprocité de Maxwell sous sa forme la plus générale.
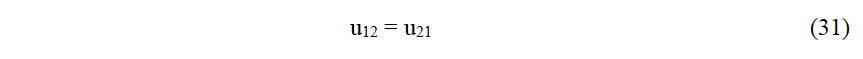
117 L’utilisation de ce principe général pour obtenir une Ligne d´influence en statique peut être vue dans la référence 1.
118 Tout ce que nous venons de voir est fondamentalement réel. Il est peut-être intéressant d´expliquer ce que signifie réel: dans le domaine des structures que nous analysons, la réalité réside dans le fait que nous pouvons utiliser une poutre réelle, la charger réellement, mesurer les déplacements et rotations des sections et vérifier les relations écrites ci-dessus. On peut aussi vérifier les résultats sur modèles réduits avec un facteur d´échelle approprié.
119 D´un autre côté, cette Réciprocité généralisée explique pourquoi on peut, pour solutionner des structures hyperstatiques par la méthode des forces, changer à chaque étape de système isostatique fondamental et pourquoi la matrice de rigidité reste symétrique dans ce cas.
120 On présente souvent ces sujets en introduisant la virtualité. Comme nous l’avons vu, cela n’est pas nécessaire. La manière de travailler est de supposer que le second état de charge est virtuel δp (x) au lieu de p(x) et son élastique aussi, δv (x) au lieu de v(x) Comme les déplacements élastiques sont toujours petits, on peut toujours les assimiler à une élastique virtuelle très petite.
121 La virtualité dans ce cas n´apporte rien de nouveau.
122 Maintenant, si nous supposons un état de charge (q(x), M2b, M2a, T2b, T2a) et ses réactions, tout réel, qui produit une élastique réelle que nous n´utilisons pas ici, et à côté une fonction élastique virtuelle w(x), avec rotations virtuelles, dérivées de l´antérieure, φ(x), la relation suivante peut s´écrire :
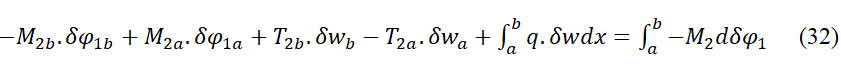
123 Le travail des charges réelles durant les déplacements virtuels est égal au travail interne des moments réels durant les rotations virtuelles.
124 Il faut dire que, dans ce cas, la relation virtuelle écrite est tout à fait indépendante du comportement du matériau ; c.à.d. que, si celui-ci n´est pas linéaire (ne suit pas la loi de Hooke), cette relation se maintient.
125 Dans ce cas il est clair que l´élastique virtuelle est une élastique qui n´est pas produite par une quelconque charge. Il n´existe même peut-être pas de charge qui pourrait produire cette fonction.
126 Nous devons reconnaître que d´habitude la virtualité est plus une façon de s´exprimer qu´une nécessité. Soit on considère comme virtuelle une élastique réelle, soit on imagine une petite variation différentielle d’une élastique réelle et on la considère comme virtuelle, soit on imagine un état de charges appelé virtuel et l’élastique virtuelle correspondante.
127 Nous avons présenté une généralisation complète de la réciprocité de Maxwell, au moyen de calculs simples. Comme nous l’avons dit au début, nous n´apportons rien de nouveau d´un point de vue pratique, mais bien sur la théorie de la réciprocité, avec une démonstration totalement générale.
128Liège, Belgique, Octobre 2017 – Córdoba, Argentina, Marzo 2018
129RÉFÉRENCES
130 Il y a tellement de publications sur les travaux de Maxwell, Betti et d´autres qu´il n´est pas utile de les citer. Quant aux développements faits par mon père la référence1 est suffisante.
Notes
1 A. Pirard, «Traité d´hyperstatique analytique et graphique», Liège, Vaillant Carmanne, 1960
2 Revista internacional de Ingeniería de estructuras, vol. 13 y 14 nº 1, 2008 – 2009 p. 89, Ecuador: “Consideración acerca de los trabajos de Lagrange sobre pandeo de columnas” por G. Pirard