Apophantique et ontologie dans la logique pure husserlienne (1901)
If you have built castles in the air, your work need not be lost; that is where they should be. Now put the foundations under them. (Henry David Thoreau)
1L’ancrage du projet husserlien de la phénoménologie dans le contexte logico-mathématique de la fin du XIXe siècle n’est aujourd’hui plus ignoré1. Son potentiel en termes de philosophie de la logique et des mathématiques a en particulier été établi grâce aux reconstructions formelles de la plupart des composants de l’idée de la logique pure dont il est l’instaurateur2, et qui, à bien des égards, préfigurent ce qui sera par la suite identifié sous le nom de logique mathématique ou formelle. Mais ce que ces reconstructions omettent en général, c’est de prendre en compte l’insertion desdits composants de la logique pure dans le système complet qu’elle constitue3, tandis que lorsque la logique pure est traitée comme un tout4, les problématiques générées par la formalisation de ses composants et/ou de leurs relations (exemplairement, celles afférentes à la conception husserlienne de la complétude) ne sont pas réellement considérées5. Cet article représente une première tentative de combler ces lacunes par le biais d’une reconstruction systématique et unitaire de la logique pure (1900/1). Et de la sorte, en situant chacun des composants de la logique pure (selon ses statut et fonction) dans l’architecture globale de l’idée husserlienne, il devrait alors en résulter une détermination précise du type de légalité (syntaxique ou sémantique) de la grammaire pure logique — ainsi que peut-être corollairement, de la relation de cette même légalité à celle, ontologique, des objets visés par et à travers elle.
Introduction : la structuration de la logique pure
2L’idée husserlienne de la logique pure intervient dans le premier volume des Recherches logiques publié en 1900. Lato sensu, elle vise à être une Wissenschaftslehre, ou en d’autres termes, un système théorique traitant des conditions de possibilité de toutes sciences, et cela, en se focalisant sur les structures logiques (a priori, analytiques, formelles) qui fondent l’unité logique des théories en général (ces dernières étant conçues comme des totalités composées d’objectivités idéales ou idéalités objectives : les significations) (Prol. : § 66 ; voir également R.L. I : § 29). Stricto sensu, elle consiste en une superposition de composants censée assurer la fondation épistémologico-transcendantale6 de la logique mathématique. Telle qu’elle est esquissée dans les Recherches logiques, elle est stratifiée sur trois niveaux7 : sub-théorique, théorique et métathéorique (Prol. : §§ 67-9) ; et ces trois niveaux sont alors scindés transversalement en deux plans qualifiées d’apophantique et d’ontologique (concernés par les domaines formels, respectivement, des significations et des objets) (R.L. IV : § 148 ; voir également R.L. I : § 29). Une telle structuration de la logique pure (voir Figure 1) — soit, sa stratification (section 1) et les relations entre ses niveaux et plans (sections 2 et 3) — forme l’objet de cet article, dont la visée tient, rappelons-le, dans la détermination de la nature et de l’opérativité nomologique de la grammaire pure logique (Conclusion).
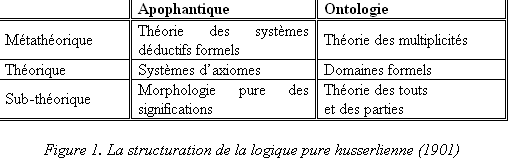
1. Les trois niveaux de la logique pure
3À suivre les Prolégomènes, le niveau sub-théorique de la logique pure husserlienne est composé de deux types (soit, apophantique et ontologique) de morphologies catégoriales (Prol. : § 67). Et sur la base des catégories et lois de connexions catégoriales de ce premier niveau est fondé son niveau théorique, alors composé de deux types de théories objectivement valides (Prol. : § 68). Quant à son niveau métathéorique, il ne constitue rien d’autre que la théorie des théories possibles en général, et simultanément de leurs domaines d’objets possibles, c’est-à-dire la science de leurs conditions de possibilité (Prol. : § 69). Ces trois niveaux scindés en deux plans sont présentés dans cette section 1 de la base au sommet.
1.1. Le niveau sub-théorique
4Les morphologies catégoriales du niveau inférieur de la logique pure sont censées établir les infrastructures transcendantales qui fondent épistémologiquement les deux niveaux supérieurs de la logique pure. À ce titre, elles traitent des catégories idéales formelles dont sont constituées les sphères apophantique et ontologique, tandis que leurs lois visent la régulation a priori de la totalité objective de combinaisons catégoriales possibles. Eu égard à la dichotomisation de la logique pure sur deux plans, ces morphologies catégoriales sont de deux types :
5— Le plan apophantique consiste dans la morphologie logico-grammaticale pure des significations (R.L. IV)9, laquelle est supposée être la théorie des significations conçues, d’un point de vue purement formel, comme les correspondants idéaux des signes signifiants (lesquels signes sont nommés expressions dans la première recherche)10 ;
6— Cependant que le plan ontologique consiste dans la théorie pure des touts et des parties (R.L. III) qui, en tant qu’ « ontologie formelle »11, est supposée être la « la théorie pure (a priori) des objets comme tels » (Husserl 1961b : 5) (soit, d’un point de vue purement formel).
7Et puisque la conception méréologique de la morphologie pure des significations (soit, ses catégories et lois) est modelée sur celle de la théorie des touts et des parties (Husserl 1961b : 85), ces deux types de morphologies catégoriales sont, du point de vue de leur compositions, strictement analogues (sous-section 3.1).
1.2. Le niveau théorique
8À son niveau intermédiaire, la logique pure est composée de systèmes d’axiomes et de domaines formels, respectivement situés sur ses plans apophantique et ontologique. Ces deux composants sont ici interdépendants — au sens où les domaines formels sont les corrélats objectifs des systèmes d’axiomes. Et ainsi, leur composition est analogue :
9— Les systèmes d’axiomes comprennent une totalité finie d’axiomes formels — mutuellement indépendants et mutuellement consistants (Husserl 1975 : 495)12 — ainsi que des lois d’opération, et lorsque lesdites lois sont utilisées pour dériver logiquement les conséquences formelles des axiomes, ils produisent une totalité nécessairement consistante de propositions ;
10— Les domaines formels sont basés sur des « multiplicités formelles », lesquelles sont conçues par Husserl comme des totalités génériques d’objets formels insérés dans des réseaux de relations (par exemple, des relations d’ordre sur des multiplicités numériques) et qui, lorsqu’elles sont spécifiées13, sont traitables par les opérations (addition, soustraction…) d’un « domaine » ou « système d’opérations »14 — cela, avec pour résultat la production d’états de choses formels (Husserl 1975 : 541-2).
11Une telle analogie dans la composition des deux plans du niveau théorique de la logique pure trace le cadre de leur mise en connexion (section 2).
1.3. Le niveau métathéorique
12Au niveau supérieur, la logique pure constitue la théorie des pures formes de théorie ressortissant au niveau théorique (y inclus ses deux plans). À l’instar de ses deux niveaux inférieurs, sa composition est ici également duale :
13— Sur le plan apophantique, la perspective métathéorique est en l’occurrence prise en charge par une théorie pure des systèmes déductifs formels, laquelle traite des formes des systèmes d’axiomes et en étudie les propriétés (telle que la correction, la complétude syntaxique, etc.) ;
14— Tandis que sur le plan ontologique, cette même perspective ressortit à la théorie des multiplicités traitant quant à elle de la forme des domaines formels15 en vue notamment de produire le classement systématique de leurs types essentiels (en tant que systèmes théoriques axiomatisés).
15Au vu de cette stratification triple de la logique pure, son niveau théorique est central. Et plus précisément, la relation entre les deux composants de ce même niveau (savoir, les systèmes d’axiomes et les domaines formels), articulant les deux plans de la logique pure, en forme le noyau — un noyau autour duquel s’articulent les statuts et fonctions de composants de la logique pure.
2. Les deux plans de la logique pure16
16La connexion des deux plans de la logique pure n’est formellement développée par Husserl qu’à son seul niveau théorique. À ce niveau, l’articulation de ses deux composants se fait le vecteur d’une relation de signification (sous-section 2.1). Et dans le cadre d’une confrontation au problème de l’imaginaire en mathématique (sous-section 2.2), le traitement métathéorique de cette relation de signification donne lieu à la dualisation putative des systèmes d’axiomes et de leurs domaines formels sous l’appellation husserlienne de définitude (sous-section 2.3).
2.1. La connexion des deux plans
17En tant qu’ « ensemble compatible de conséquences formelles » (Husserl 1975 : 531), un système d’axiomes délimite une sphère formelle d’objets au sein de la totalité des objets formels possibles. Une telle délimitation est conçue par Husserl comme un processus d’identification en deux temps, successivement gouvernés par un ensemble de conditions.
181. Le processus d’identification d’un domaine formel par son système d’axiomes est d’abord caractérisé en tant que définition « indéterminée », et cette dernière requiert la présence d’ « axiomes d’existence » pour chacune des opérations exploitées dans le domaine formel17, ainsi que l’adjonction d’un « axiome de fermeture » excluant toute possibilité d’élargissement du système d’axiomes auquel il s’ajoute18.
192. Quand la première condition de l’obtention d’une définition indéterminée (soit, celle concernant la présence d’axiomes d’existence) est satisfaite, l’identification d’un domaine formel par son système d’axiomes peut alors être perfectionnée de manière à obtenir une définition déterminée19.
20À terme, lorsque la détermination est parfaite, la spécification du domaine formel est ultime. Et dans un tel cas, le domaine formel en question constitue alors une multiplicité dite « constructible » ou encore « mathématique »20 (Husserl 1975 : 515-6, 556).
2.2. Le problème de l’imaginaire en mathématique
21Le lien articulant un système d’axiomes à son domaine formel cadre la formulation dudit “problème de l’imaginaire en mathématique” (Husserl 1975 : app. VI21). Brisant « le sens propre, originairement visionné » dans les « procédés purement symboliques » des mathématiques pures pour l’inverser en « contre-sens », le problème du passage par l’imaginaire est présenté par Husserl (1975 : 375) en 1913 comme le motif de sa focalisation sur « le caractère purement signitif et purement linguistique du processus de la pensée et de la connaissance », puis de sa quête d’un « éclaircissement universel du sens » dans le cadre de la logique pure (dès lors conçue en tant que fondation épistémologique transcendantale de la logique formelle). Et aiguillant de la sorte le cours des investigations philosophico-mathématiques de Husserl dès le début des années 1890 (Husserl 1950 : § 72, note ; 1957 : § 31), ce problème concerne l’utilisation, dans un calcul opérant sur un domaine formel (plus exactement, sur la multiplicité à la base de ce domaine), d’éléments qui, selon son propre système d’axiomes, sont inexistants dans ce domaine (voir l’exemple 1 ci-dessous). Dans ce contexte, il met en jeu la question de la conservativité et de la consistance de l’extension d’un système d’axiomes (Husserl 1975 : 496-7, 1957 : 132-3) (cf. l’exemple 2 ci-dessous). Ce qui en sens inverse peut se reformuler comme suit : À quelle condition est-il possible d’élargir un système d’axiomes (par l’ajout d’axiomes indépendants pour les « imaginarités » en cause) sans entraîner de contradiction ? et : À quelle condition une extension consistante d’un système d’axiomes est-elle conservative (sur le domaine formel corrélatif élargi) ?22 C’est pour traiter ces questions que Husserl introduit alors ses notions de définitude.
22Exemple 1 (Emprunté à da Silva 2000a : 418).Soit N, l’ensemble des nombres naturels (c’est-à-dire, la plus petite relation contenant 0 et close pour l’opération de succession (S)), avec l’addition récursivement ainsi : pour tout n, m appartenant à N : n + 0 = n ; n + (S (m)) = S (n + m). Supposons maintenant l’élargissement arbitraire de N par des éléments imaginaires – n définis comme les uniques éléments, pour chaque n respectivement, tels que n + (– n) = 0 [*] : ces “imaginarités mathématiques” sont inexistants pour N, cependant que leur propriété définitionelle [*] est sans sens dans N élargi par l’ajout des imaginarités – n (de fait, telle qu’ici définie l’addition ne fait sens que pour N) ou lorsque l’addition est restreinte aux nombres entiers.23
23Exemple 2 (Emprunté à da Silva 2000a : 420).Dans N élargi par l’ajout des nombres négatifs, il est possible de prouver (à l’aide d’un ensemble d’axiomes satisfaisant pour N) que pour tout n, m, k appartenant à N : n + k = m + k => n = m ; mais cela est également prouvable comme suit (à l’aide des nombres négatifs, de leur propriété définitionnelle [*], ainsi qu’avec certaines des propriétés générales de l’addition) : n + k = m + k => (n + k) + (–k) = (m + k) + (–k) => n + (k + (–k)) = m + (k + (–k)) => n + 0 = m + 0 => n = m : cependant, pour N, seules la première et les deux dernières équations sont pourvues de sens, quoique ce que la dérivation prouve est vrai.
2.3. Les notions de définitude
24Les recherches menées par Husserl sur l’extension des systèmes formels au niveau théorique suscite l’identification, au niveau métathéorique, d’une propriété intrinsèque à certains des systèmes d’axiomes définissant leur domaines respectifs de manière déterminée — soit à des systèmes d’axiomes clos de manière interne (sans adjonction extrinsèque d’axiome de fermeture) qui déterminent complètement leurs domaines formels (sous-section 1.3). Étiquetée par Husserl du terme de définitude, cette propriété peut être interprétée comme une forme de complétude déductive impliquant l’idéal d’une dualisation des systèmes d’axiomes et de leurs domaines formels24. Sous cette appellation, elle est alors spécifiée en deux types distincts, respectivement qualifiés de relatif et d’absolu — eu égard à la portée de la complétude déductive du système qualifié (valide dans les limites de son domaine formel en cas de définitude relative, valide en général en cas de définitude absolue)25. Et par le biais de cette spécification, la définitude husserlienne est supposée permettre de solutionner le problème de l’imaginaire en mathématique en ces termes : Une extension conservative et consistante d’un système d’axiomes (par l’ajout d’axiomes indépendants pour des “imaginarités mathématiques”) est possible si le système d’origine est relativement « défini » et si l’extension est opérée dans la sphère d’un système d’axiomes absolument « défini »26. Quoi qu’il en soit, la dualisation syntaxico-sémantique impliquée dans la notion de définitude en elle n’est toujours que supposée, sans jamais être démontrée (ni même à démontrer). Et ici, mon hypothèse est que, caractérisant la relation liant un système d’axiomes à son domaine formel en tant que relation de signification, la justification de cette même notion réside dans son intégration et sa fondation dans l’architecture globale de la logique pure (voir Figure 1) — c’est-à-dire, selon les articulations internes de cette dernière27.
3. Les articulations internes de la logique pure
25La base de la logique pure est constituée sur ses deux plans par des morphologies catégoriales — à savoir, par la morphologie (logico-grammaticale) pure des significations et la théorie des touts et des parties (sous-section 1.1). Ces morphologies sont mises en œuvre théoriquement sur le principe d’une distinction entre deux types d’entités : les entités « simples » et les entités « complexes ». Et, cette distinction ayant pour critère la décomposabilité de l’entité en question en une pluralité de parties articulées (R.L. III : §1), lesdites morphologies se focalisent sur la relation de composition du complexe par le simple (soit, des touts par les parties). En conséquence, chacune de deux morphologies constitue une méréologie28 (sous-section 3.1). Subdivisées en deux sphères (sous-section 3.2), elles sont ce qui fonde la relation de signification propre au niveau théorique de la logique pure husserlienne (sous-section 3.3).
3.1. Les morphologies catégoriales en tant que méréologies
26La constitution des morphologies catégoriales en tant que méréologies procède29 :
271) à l’établissement des deux catégories formelles fondamentales d’objet et de signification, que sont en l’espèce :
28• D’un côté, la catégorie de l’indépendance caractérisant des entités autonomes — soit, des entités non nécessairement intégrées dans des touts (et qui, lorsqu’elles le sont, préservent leur indépendance à l’endroit du tout, ainsi qu’au sein du tout, envers ses autres parties : cela forme en conséquence des entités « complètes »),
29• De l’autre, la catégorie de la non-indépendance qui quant à elle caractérise des entités non-autonomes — soit des entités nécessairement intégrées dans des touts (et qui sont dépendantes du tout en tant que parties, et dépendantes des autres parties au sein du tout : cela forme alors des entités « incomplètes ») ;
302) à la formulation des lois qui régulent la totalité des combinaisons (syntaxiques) possibles entre ces deux types de catégories formelles fondamentales (et leurs spécifications) dans le processus de formation d’entités complexes à partir d’entités simples, et plus précisément : les entités simples « en entrée » comprennent autant des entités de type autonome que non-autonome (toutes étant traitées en tant que parties dans le processus de leur combinaison)30, et en cas de compatibilité, il en résulte (« en sortie ») des touts par complémentation de parties — c’est-à-dire des unités complexes de parties compatibles connectées par un lien de fondation (à savoir, des parties elles-mêmes dans le tout) (R.L. III : § 23 ; IV : § 10)31.
31Et sur cette base, l’objectif des morphologies méréologiques husserliennes est d’obtenir le sous-ensemble de toutes les combinaisons catégoriales possibles de leurs domaines respectifs — soit, la totalité itérativement close des toutes les formes possibles d’objets et de significations (R.L. III : § 24 ; IV : §§ 10, 13).
3.2. Les deux sphères des morphologies catégorielles
32La totalité des combinaisons méréologiques des catégories formelles propres à chacune des deux morphologies est stratifiée sur deux niveaux respectivement qualifiés de sphères logiques inférieure et supérieure (R.L. IV : § 14, rem. 3), lesquelles sont gouvernées par des lois de natures complètement différentes (R.L. IV : intro. et § 14).
3.2.1. La sphère morphologique inférieure
33Au niveau inférieur, le critère opérationnel est la bonne formation des touts par les parties. Et en fonction de sa satisfaction ou non, le produit obtenu “en sortie” forme soit une combinaison unitaire (composée de parties morphologiquement compatibles), soit une combinaison non unitaire (alors composée de parties morphologiquement incompatibles). Ainsi :
34— Dans le cas apophantique (savoir, celui de la morphologie pure des significations), cette distinction correspond en l’occurrence à l’opposition du sens et du non-sens (Unsinn)32 ;
35— Tandis que dans le cas ontologique, il devrait lui correspondre une distinction entre des possibilités et impossibilités objectives absolues (c’est-à-dire, entre des objets ou états de choses possiblement existants et des combinaisons nécessairement inexistantes).33
36Cette première sphère méréologique conditionne de la sorte la possibilité même de la sémanticité. D’une part, en déterminant la possibilité, pour n’importe quel composé sémiotique, de posséder une signification (c’est-à-dire, de faire sens). Et d’autre part, symétriquement, en déterminant la possibilité, pour n’importe quel composé ontologique, d’être un corrélat référentiel (c’est-à-dire, d’exister comme objet) (R.L. I : § 29).
3.2.2 La sphère morphologique supérieure
37Quant au niveau supérieur, il représente une spécification en deux types distincts de la combinaison unitaire de parties morphologiquement compatibles — soit, du cas de satisfaction du critère opératif au niveau inférieur (sous-section 3.2.1). Le critère de distinction de ces deux types d’entités complexes est alors la consistance des touts en question eu égard à leurs parties composantes. Et en fonction de la satisfaction ou non d’un tel critère, le produit obtenu « en sortie » forme une combinaison unitaire, respectivement, de compatibilités ou incompatibilités objectives. Ainsi :
38— Dans le cas apophantique, cette distinction correspond en l’occurrence à l’opposition du sens « accordé formellement avec lui-même » (Husserl 1961b :130) et du contre-sens (Widersinn)34 ;
39— Tandis que dans le cas ontologique, il correspond à la distinction entre des possibilités et impossibilités objectives relatives (c’est-à-dire, entre des possibilités d’existence et de non-inexistence d’objets en tant que déterminés par un système de significations)35.
40Cette seconde sphère méréologique conditionne de la sorte la possibilité même de toute sémantisation (soit, de toute valuation sémantique). Ce qui est alors ici déterminé est la possibilité, pour n’importe quel composé sémiotique doté de signification, d’être interprétable ; et symétriquement, la possibilité, pour n’importe quel complexe objectal, d’être le corrélat référentiel interprétant un composé sémiotique doté de signification (R.L. I : § 29).
3.3. Les relations de fondations
41La stratification en deux sphères des morphologies catégoriales accomplit la jonction des deux niveaux inférieurs de la logique pure elle-même. Du point de vue de la structuration globale de cette dernière, la jonction en question est une relation de fondation. Et ce que cette relation indique, c’est le conditionnement transcendantal du niveau théorique de la logique pure par son enracinement sub-théorique (R.L. I : §29 ; voir également Husserl 1975 : 546). Ainsi, sur le plan apophantique, la morphologie logico-grammaticale des significations est ce qui fonde les systèmes d’axiomes, voire peut-être plus précisément les axiomes « structurels » — avec ici les catégories de signification fondant les axiomes relatifs aux objets et les lois de combinaisons apophantico-catégoriales, les axiomes portant sur les relations (voir note 13)36. Alors que sur le plan ontologique, la théorie des touts et des parties fonde les domaines formels, voire peut-être plus strictement les multiplicités formelles à la base de ces derniers — avec ici les catégories objectives fondant les objets formels des multiplicités et les lois de combinaisons ontologico-catégoriales, les réseaux de relations unifiant ses objets37. Et de la sorte, la jonction en jeu serait scellée et la fondation opérée.
Conclusion
42Au terme de cet article, la logique pure husserlienne (1900/1) a été systématiquement et unitairement reconstruite. Dans le cadre de cette reconstruction, elle apparaît comme étant conçue pour justifier la dualité possible de la relation de signification en jeu à son niveau théorique (section 2) — à savoir, de la relation articulant un système d’axiomes à son domaine formel (section 1). Le statut de la morphologie logico-grammaticale pure des significations à l’endroit de cette relation est alors d’être le fondement des systèmes d’axiomes, et sa fonction, de les fonder (sous-section 3.3). Or, par le biais de cette articulation fondationnelle des deux niveaux inférieurs du plan apophantique de la logique pure, le type de légalité de ladite morphologie est enfin précisément déterminable. En l’occurrence, ce type se révèle être double, déterminant autant l’exclusion des combinaisons de significations insensées parce que composées de parties morphologiquement incompatibles (soit, de combinaisons mal formées), que l’exclusion des combinaisons de significations contradictoires parce que composées de parties objectivement incompatibles (soit, de combinaisons non interprétables) (sous-section 3.2). Conditionnant de la sorte successivement la sémanticité et la sémantisation possibles de tout composé sémiotique, la nature et l’opérativité des lois logico-grammaticales de la morphologie pure des significations ne sont donc en définitive pas seulement celles de lois morphosyntaxiques à la base des systèmes d’axiomes, mais aussi également celles de lois sémantiques conditionnant la possibilité même de leur mise en relation à un domaine formel. Et suivant pareille prévalence du plan apophantique sur le plan ontologique au sein de la logique pure, le corrélat objectal d’un composé sémiotique pourvu de signification sera ici déterminé par la structure des significations au moyen desquelles il est visé38.
Bibliographie
Benoist, Jocelyn (1997). Phénoménologie, sémantique, Ontologie. Paris : Presses universitaires de France.
— (2001). Intentionnalité et langage dans les Recherches logiques de Husserl. Paris : Presses universitaires de France.
Casari, Ettore (2000). On Husserl’s Theory of Wholes and Parts. History and Philosophy of Logic 21 (1), 1-43.
Centrone, Stefania (2010). Logic and Philosophy of Mathematics in the Early Husserl. Dordrecht : Springer.
Correia, Fabrice (2004). « Husserl on Foundation ». Dialectica 58 (3), 349-367.
da Silva, Jairo José (1999). « Husserl’s Conception of Logic ». Manuscrito 22 (2), 367-397.
— (2000a). « Husserl's Two Notions of Completeness. Husserl and Hilbert on Completeness and Imaginary Elements in Mathematics ». Synthese 125 (3), 417-438.
— (2000b), « The Many Senses of Completeness ». Manuscrito 23 (2), 41-60.
— (2015), « Husserl and Hilbert on Completeness, still ». Synthese. doi:
10.1007/s11229-015-0821-2.
Fine, Kit (1995). « Part-Whole ». B. Smith, D. Woodruff Smith (éds.), Cambridge Companion to Husserl, New York : Cambridge University Press, 463-485.
Frege, Gottlob (1971). Écrits logiques et philosophiques. Trad. Claude Imbert. Paris : Seuil.
Gutzmer, August (1902). « VI. Mitteilungen und Nachrichten. 1. Akademie. Gesellschaften. Vereinigungen. Versammlungen ». Mathematische Gesellschaft zu Göttingen. Jahresbericht der Deutschen Mathematiker-Vereinigung 11, 71, 147, 202, 302, 356, 426.
Hartimo, Mirja Helena (2007). « Toward Completeness: Husserl on Theory of Manifolds 1890-1901 ». Synthese 156 (2), 281-310.
— (2012). « Husserl and the Algebra of Logic: Husserl’s 1896 Lectures ». Axiomathes 22 (1), 121-133.
Hill, Claire Ortiz (1995). « Husserl and Hilbert on Completeness ». In J. Hintikka (éd.), From Dedekind to Gödel. Essays on the Development of the Foundations of Mathematics. Éd. Jakko Hintikka. Dordrecht : Kluwer, 143-163.
— (2002). « Tacking Three of Frege’s Problems: Edmund Husserl on Sets and Manifolds ». Axiomathes 13 (1), 79-104.
— (2003). « Incomplete Symbols, Dependent Meanings and Paradox ». In D. O. Dahlstrom, (éd.), Husserl’s Logical Investigations. Dordrecht : Kluwer, 69-93.
— (2010a), « On Fundamental Differences between Dependent and Independent Meanings ». Axiomathes 20 (2-3), 313-332.
— (2010b), « Husserl on Axiomatization and Arithmetic ». In M. H. Hartimo (éd.), Phenomenology and Mathematics. Dordrecht : Springer, 47-71.
Hill, Claire Ortiz & Rosado Haddock, Guillermo Ernesto (2000). Husserl or Frege? Meaning, Objectivity and Mathematics. Lasalle : Open Court.
Husserl, Edmund (1950). Idées directrices pour une phénoménologie. Introduction générale à la phénoménologie pure. Trad. Paul Ricœur. Tome 1. Paris : Gallimard.
— (1957). Logique formelle et logique transcendantale. Essai d’une critique de la raison logique. Trad. Suzanne Bachelard. Paris : Presses universitaires de France.
— (1959). Recherches logiques. Prolégomènes à la logique pure. Trad. Hubert Élie, Arion Lothar Kelkel et René Schérer. Tome 1. Paris : Presses universitaires de France.
— (1961a). Recherches logiques. Recherches I et II. Trad. Hubert Élie, Arion Lothar Kelkel et René Schérer. Tome 2-1. Paris : Presses universitaires de France.
— (1961b). Recherches logiques. Recherches III, IV et V. Trad. Hubert Élie, Arion Lothar Kelkel et René Schérer. Tome 2-2. Paris : Presses universitaires de France.
— (1963). Recherches logiques. Éléments d’une élucidation phénoménologique de la connaissance. Recherche VI. Trad. Hubert Élie, Arion Lothar Kelkel et René Schérer. Tome 3. Paris : Presses universitaires de France.
— (1975). Articles sur la logique (1890–1913). Trad. Jacques English. Paris : Presses universitaires de France.
— (1996). U. Panzer (éd.), Logik und allgemeine Wissenschaftstheorie. Vorlesungen 1917/18. Mit ergänzenden Texten aus der ersten Fassung von 1910/11.. Husserliana 30. Dordrecht : Kluwer.
— (1998). Introduction à la logique et à la théorie de la connaissance. Cours 1906–1907. Trad. Laurent Joumier. Paris : Vrin.
— (2003). Philosophy of Arithmetic. Psychological and Logical Investigations. With Supplementary Texts from 1887-1901. Trad. Dallas Willard. Dordrecht : Kluwer.
Ierna, Carlo (2011), « Der Durchgang durch das Unmögliche. An Unpublished Manuscript from the Husserl-Archives ». Husserl Studies 27 (3), 217-226.
Isaac, Manuel Gustavo (2015). « L’idée de la logique formelle dans les appendices VI à X du volume 12 des Husserliana (1970) ». History and Philosophy of Logic 36 (4), 321-345.
— (2016). « Widersinn in Husserl’s Pure Logic ». Logica Universalis. doi:
10.1007/s11787-015-0135-7.
— (à paraître). A. Pietarinen, M. Shafiei (éds.), « Pure Logic from the Semiotic Standpoint of Intentionality ». Husserl and Peirce. Dordrecht : Springer.
Rollinger, Robin D. (2003). « Husserl’s Elementary Logic. The 1896 Lectures in their Nineteenth Century Context ». Studia Phænomenologica III (1-2), 195-213.
Rosado Haddock, Guillermo Ernesto (1997), « Husserl’s Relevance for the Philosophy and Foundations of Mathematics ». Axiomathes 8 (1-3), 125-142.
— (2006). « Husserl’s Philosophy of Mathematics: its Origin and Relevance ». Husserl Studies 22 (3), 193-222.
Schuhmann, Elisabeth & Schuhmann, Karl (2001). « Husserl Manuskripte zu seinem Göttinger Doppelvertrag von 1901 », Husserl Studies 17 (2), 87-123.
Smith, Barry (1982). Parts and Moments. Studies in Logic and Formal Ontology. München & Wien : Philosophia Verlag.
Smith, David Woodruff (2002). « What is ‘Logical’ in Husserl’s Logical Investigations? The Copenhagen Interpretation ». In D. Zahavi, F. Stjernfelt (éds.), One Hundred Years of Phenomenology. Husserl’s Logical Investigations Revisited. Dordrecht : Kluwer, 51-65.
Tieszen, Richard L. (2008). « Husserl’s Concept of ‘Pure Logic’ ». In V. Mayer (éd.), Husserl: Logische Untersuchungen. Berlin : Akademie Verlag, 9-26.
Notes
1 Outre certains des travaux de Husserl en philosophie de la logique et des mathématiques datés au tournant du siècle et publiés pour partie en appendice au volume 12 des Husserliana (Husserl 1975 : app. VI-X), cet article est rédigé exclusivement à partir des Recherches logiques et sans tenir compte des inflexions successives subies par l’idée de la logique pure dans l’œuvre husserlienne ultérieure (Husserl 1957, 1996, 1998).
2 Sur la théorie des touts et des parties, cf. Casari 2000 ; Correia 2004 ; Fine 1995 et l’essai de Simons dans Smith 1982. Sur la théorie des multiplicités, cf. Centrone 2010 : chap. 3 ; da Silva 2000a, 2000b, 2015 ; Hartimo 2007 ; Hill 1995 ; Hill & Rosado Haddock 2000 : chap. 9 et Isaac 2015. Enfin, sur le calcul logique de Husserl, cf. Centrone 2010 : app. 5 ; Hartimo 2012 et Rollinger 2003.
3 Les exceptions sont ici notamment da Silva 2015 et Hill 2002, 2003, 2010a, 2010b, ainsi Mulligan & Smith, Simons, Willard et Null & Simons dans Smith 1982.
4 Comme par exemple dans Centrone 2010 : chap. 2 ou encore da Silva 1999.
5 Outre Smith 2002 (et dans une moindre mesure, Tieszen 2008), une exception notable est ici Rosado Haddock 2006 (cf. e.g. Haddock 1997).
6 Le syntagme adjectival épistémologico-transcendantal désigne ici le motif husserlien d’une « compréhension critique de la logique en tant que science » et en termes de théorie de la connaissance (Husserl 1959 : ix) ; plus généralement, eu égard à la focalisation des recherches de Husserl sur « le rapport entre la subjectivité du connaître et l’objectivité du contenu de la connaissance » (ibid.), le terme d’épistémologie (et ses dérivés) sera employé dans cet article pour signifier conjointement les théories de la science et de la connaissance.
7 La terminologie à suivre n’est évidemment pas husserlienne.
8 La distinction de deux plans de la logique pure est opérée par Husserl à chacun des trois niveaux de sa stratification (Prol. : §§ 67-9). Cf. l’« Esquisse d’une Préface aux Recherches logiques (1913) », publiée en 1939 (Husserl 1975 : 369-70, 380-1) ; la qualification de ces deux plans par les épithètes d’apophantique et d’ontologique procède ici d’une extension de l’emploi de ces derniers au paragraphe 14 de la seconde édition des Recherches logiques (1913) — emploi apparemment restreint au niveau ici identifié comme sub-théorique (cf. Husserl 1998 : § 18).
9 L’épithète logico-grammatical est une adjonction de 1913 au titre du paragraphe 13 de la quatrième Recherche.
10 Cette correspondance explique que la distinction des significations dépendantes et indépendantes (section 3.1) procède en partie de la distinction médiévale du catégorématique et du syncatégorématique appliquée aux signes ou expressions (R.L. IV : §§ 4, 5).
11 Identifiant une partie du projet méréologique husserlienne (à savoir, sa partie analytique et non matérielle), le syntagme d’ontologie formelle est également une adjonction de Husserl (1961b : 6) datée de 1913 — cf. l’ « Esquisse de Préface » mentionnée en note 2 de la page précédente (Husserl 1975 : 360, 372-3, 387-8).
12 Il est en fait possible de distinguer trois types d’axiomes dans les textes de Husserl datés du tournant du siècle (Husserl 1975 : app. VI-X) : les axiomes décrivant les objets des domaines formels, ceux qui expriment les propriétés des relations dans tel domaine formel (par exemple, la linéarité d’une relation d’ordre sur les objets du domaine en question) et enfin, ceux qui sont relatifs aux propriétés des opérations dans un domaine formel (typiquement, l’associativité, la commutativité, etc. de tel de ses opérateurs) ; les domaines formels qu’ils caractérisent étant généralement des théories algébriques, leur forme est celle d’équations (Husserl 1975 : 503).
13 Plus précisément, l’existence des relations formelles unifie la multiplicité, cependant que leur forme (définie par les axiomes du domaine formel) est ce qui la spécifie — c’est-à-dire distingue ses composants formels (objets et relations) en tant qu’espèce(s) d’une multiplicité générique.
14 En d’autres termes, les opérations d’un domaine d’opérations opèrent sur des multiplicités considérées en tant que composées d’espèces de formes d’objets et de relations (Husserl 1975 : 535, 539, 543-4).
15 Plus spécifiquement, de la forme de multiplicités formelles définies de manière déterminée qui en tant que telle constitue lesdites « multiplicités mathématiques » ou « constructibles » (sous-section 2.1).
16 La rédaction de cette section repose principalement sur les essais posthumes publiés en appendices au volume 12 des Husserliana (Husserl 1975 : app. VI-X).
17 Le rôle de tels axiomes est d’assurer l’application des opérations en usage dans le domaine d’opérations — par exemple, si la combinaison « + » est présente dans le domaine formel, alors il doit y avoir en son sein deux objets a et b combinables sous la forme “a + b” et au moins un élément x tel que x = a + b (Husserl 1975 : 531-2).
18 L’adjonction d’un axiome de fermeture étant toujours extrinsèque à un système d’axiomes, il s’agit d’un axiome négatif, et à ce titre, le système d’axiomes en question est alors seulement clos de manière externe (Husserl 1975 : 504).
19 Dans ce cas, le système d’axiomes du domaine en question doit être tel que (Husserl 1975 : 534) : 1/ aucune nouvelle détermination ne puisse être ajoutée à la caractérisation du domaine formel par les axiomes de son systèmes d’axiomes — à cet égard, le système d’axiomes concerné est clos de manière interne (cf. la précédente note) ; 2/ il soit possible d’identifier univoquement, par le biais des axiomes, chacun des éléments de la multiplicité à la base du domaine — et à cet égard, le domaine formel est complètement déterminé.
20 C’est-à-dire, un domaine formel (impossible à spécifier plus avant) dans lequel ce qui seul reste à déterminer est l’identité singulière de son contenu matériel.
21 Cf. Schuhmann & Schuhmann 2001 ; Husserl 2003 : B. Essay III et Ierna 2011.
22 Dans Logique formelle et logique transcendantale, les deux questions sont confondues dans les termes suivants : « Jusqu’où s’étend la possibilité d’“élargir” une “multiplicité”, un système déductif bien défini en un système nouveau qui contient comme “partie” l’ancien ? », Husserl 1957 : 133.
23 Pour une typologie des incompatibilités des significations en jeu au niveau théorique de la logique pure, cf. Isaac 2016.
24 Une telle complétude requiert que pour chaque proposition pourvue de signification pour/compréhensible par le système d’axiomes, soit elle-même, soit sa négation est dérivable par le système d’axiomes et qu’elle est en conséquence respectivement valide ou non-valide dans le domaine formel corrélé — ainsi : « Dans une multiplicité définie de type mathématique on peut poser l’équivalence de ces deux concepts : “vrai” et ”conséquence formelle des axiomes”, de même celle des concepts : “faux” et “conséquence contraire formelle des axiomes” » (Husserl 1950 : 232) ; néanmoins, la signification de la notion husserlienne de définitude continue de faire débat sans qu’un consensus ne soit à ce jour atteint (cf. Centrone 2010 : chap. 3 ; da Silva 2000a, 2000b, 2015 ; Hill 1995 ; Hartimo 2007 ; Isaac 2015).
25 Dans le texte : « Un système d’axiomes est “défini” de manière relative si toute proposition qui a un sens pour lui est décidée dans la limitation au domaine de ce système ; un système d’axiomes est “défini” d’une manière absolue si toute proposition qui a un sens d’après lui est décidée en général. » (Husserl 1975 : 502) ; cette distinction fait l’objet de Centrone 2010 : 3.6.1 ; da Silva 2000a : 3, 4 ; Hartimo 2007 : 303 sq.. ; Isaac 2015 : 4.2.
26 Cf. Husserl 1975 : 503, 517 ; 1957 : 133, ainsi que la recension de la seconde des deux Conférences de 1901 devant la Société mathématique de Göttingen (Gutzmer 1902 : 147).
27 Inversement, il est possible d’interpréter la stratification triple de la logique pure comme résultant de l’exigence d’une justification de l’idéal de dualisation véhiculé par la notion de définitude — et donc indirectement, comme réponse au problème de l’imaginaire en mathématiques (section 2.2).
28 Sur l’élaboration progressive du thème de la méréologie chez Husserl entre 1887 et 1901, cf. Benoist 2001 : chap. 1.
29 À propos des deux étapes de ce processus, quoiqu’avec compréhension radicalement divergente du statut de la méréologie ontologique à l’endroit de la grammaire pure, se reporter à Benoist 1997 : chap. 5.
30 Les parties non-indépendantes sont ici à l’évidence nécessaires dans le processus de formation d’entités complexes à partir d’entités simples (corrélativement à la focalisation des morphologies catégoriales sur la relation de dépendance, autrement dit, de fondation) (R.L. IV : § 10) — cf. les remarques de Frege en 1891/2 touchant à la relation liant une fonction insaturée ou incomplète à son argument quant à lui clos sur soi (Frege 1971 : 84sq., 140) (à propos des notes personnelles de Husserl en réaction aux articles de Frege, cf. Hill 2003 : section 7).
31 Sur le concept de fondation, se reporter au paragraphe 13 de la troisième Recherche (pour des développements techniques, consulter les références mentionnées dans la première note du texte).
32 Par exemple, un homme raisonnable ou un carré non-carré forment des combinaisons unitaires de parties (indépendantes et non-indépendantes) morphologiquement compatibles, c’est-à-dire forment du sens; tandis que vert est ou forme une combinaison non unitaire de parties morphologiquement incompatibles (toutes étant en l’occurrence non-indépendantes), c’est-à-dire forme du non-sens.
33 Par exemple, les états de choses homme–raisonnable ou carré–non-carré (où non-carré est une propriété) forment des combinaisons unitaires de parties (indépendantes et non-indépendantes) morphologiquement compatibles, c’est-à-dire forment des états de choses possiblement existants; tandis que vert-est-ou forme une combinaison non unitaire de parties (en l’occurrence, non-indépendantes) morphologiquement incompatibles, c’est-à-dire forme une combinaison nécessairement inexistante.
34 Par exemple, un homme raisonnable forme une combinaison unitaire de parties objectivement compatibles (et ainsi non-contradictoire), tandis que un carré non-carré forme une combinaison unitaire de parties objectivement incompatibles (et ainsi contradictoire).
35 Par exemple l’état de choses homme–raisonnable forme une combinaison unitaire de parties objectivement compatibles (et relativement existantes), tandis que l’état de choses carré–non-carré forme une combinaison unitaire de parties objectivement incompatibles (et relativement inexistantes) — ce signalement de relativité est ici en adéquation avec la détermination des domaines formels par leurs systèmes d’axiomes (sous-section 2.1).
36 Aucune attestation textuelle ne supporte à ma connaissance pareille interprétation, ici purement conjecturale.
37 Voir cependant la mise en garde de la note précédente.
38 Sur ce point, cf. Isaac (à paraître).

