Valeria Giardino

L’imagination manipulatoire en mathématique

Documenten bij dit artikel

Bijlagen

• Texte complet en PDF/Full text in PDF: Vol. XIII, n°2 (209k)

Résumé

L’objectif de cet article est double. D’abord, nous introduirons une notion d’imagination qui s’avérera être un élément crucial en mathématique. Dans des travaux précédents, nous avons analysé la pratique de la topologie et nous avons proposé que l’expertise en topologie a une certaine familiarité avec ce que nous avons défini comme étant l’« imagination manipulatoire ». Cette forme d’imagination s’avère centrale dans de nombreux domaines de la topologie, par exemple la théorie des nœuds1, la topologie en basses dimensions2 et la théorie des tresses3. Ensuite, nous présenterons une caractérisation possible de l’imagination manipulatoire basée sur la notion d’imagination comme « faire semblant » qui a été proposée par Walton4. Nous ferons aussi l’hypothèse que cette caractérisation « waltonienne » peut être mieux spécifiée si on étend aux représentations la notion de « potentialité » introduite par Gibson5.

Inhoudstafel

1. L’« embodied mathematics » et ses deux interprétations possibles

1L’imagination a-t-elle un rôle fondamental en mathématique ? Et si c’est le cas, comment peut-on la caractériser ? Dans cet article, on cherchera à répondre à ces deux questions. D’abord, on introduira une notion d’imagination dont nous nous sommes occupés dans des travaux précédents dédiés en particulier à la topologie ; ensuite, on cherchera à donner une caractérisation satisfaisante de ce type d’imagination. Avant de s’interroger sur le rôle de l’imagination en mathématiques, on présentera le contexte philosophique plus large qui rend particulièrement intéressantes ces questions.

2Ces dernières années, plusieurs travaux ont eu comme objectif de mettre en évidence le rôle du corps dans la cognition, non seulement dans la pensée ordinaire mais aussi et en particulier dans la pensée mathématique. Aujourd’hui on parle souvent d’« embodied cognition », mais plusieurs théories — ou étiquettes ? — alternatives ont été proposées, telles que « embedded cognition », « enactivism », « extended mind », « situated cognition », « grounded cognition »6, et ainsi de suite7. On ne va pas discuter ici des différences entre ces positions distinctes, ce qui mériterait un traitement à part ; cependant, on voit facilement quelle est leur thèse négative, c’est-à-dire l’approche à la cognition à laquelle elles s’opposent. Les théories « standard » en sciences cognitives ont affirmé que les représentations impliquées dans les connaissances fondamentales ont un format amodal, c’est-à-dire qu’elles sont traitées indépendamment des systèmes modaux du cerveau dédiés à la perception, à l’action et à l’introspection8. Au contraire, les approches qui défendent l’idée de la cognition comme « embodied » nient que ceci soit vrai : la perception, l’action et l’introspection peuvent en fait influencer la manière dont nous connaissons. Comme Barsalou le souligne :

Following the cognitive revolution in the mid-twentieth century, theorists developed radically new approaches to representation. In contrast to pre-twentieth century thinking, modern cognitive scientists began working with representational schemes that were inherently nonperceptual. To a large extent, this shift reflected major developments outside cognitive science in logic, statistics, and computer science9.

3Selon les approches « embodied », la révolution cognitive des années 1950 a eu donc comme désavantage d’avoir fait oublier l’apport de la perception — et donc du corps, et des boucles sensorimotrices — à la cognition, et à la connaissance en général.

4Une critique parallèle se retrouve dans certaines théories sur la nature des connaissances mathématiques. Plusieurs études récentes, qui peuvent être regroupées sous l’étiquette d’« embodied mathematics », ont rejeté les théories classiques des mathématiques. Selon ces théories standard, les mathématiques s’occupent d’objets abstraitsdécrits par des signes mais qui n’ont aucune propriété en commun avec les objets ordinaires ; cela signifie qu’on peut distinguer nettement la connaissance abstraite de nos connaissances qui résultent de nos rencontres avec le monde concret. En revanche, les approches qui s’intéressent aux mathématiques en tant qu’« embodied » remettent en cause une telle distinction : selon ces approches, les théories standard n’arrivent pas à expliquer la nature des connaissances mathématiques, parce que l’on peut montrer que même en travaillant avec des objets abstraits les êtres humains exploitent certaines compétences et capacités qu’ils utilisent typiquement dans leurs interactions avec les objets concrets.

5Pour mieux comprendre les thèses positives de ces approches, nous proposons de distinguer deux interprétations de l’« embodied mathematics » (ci-après EM). D’abord, on peut parler d’une interprétation conceptuelle de l’EM, qui défend l’idée que les notions mathématiques sont conceptualisées par le biais de métaphores fondamentales qui se basent sur l’expérience corporelle. Cette interprétation du caractère « embodied » des mathématiques a été proposée par Lakoff et Núñez dans un livre qui date déjà de presque vingt ans10, où les auteurs ont soutenu que nous comprenons les concepts scientifiques abstraits ainsi que les concepts ordinaires en terme de métaphores.

6Pour donner un exemple, les expressions suivantes sont très répandues : on dit communément que les nombres naturels « croissent » indéfiniment, ou que les points « se trouvent » sur une droite, ou encore que les fonctions « tendent » vers 0, même si les nombres bien évidemment ne peuvent pas littéralement croître, ni se trouver quelque part, ni tendre vers quelque état non plus. En fait, selon Lakoff et Núñez, les mécanismes cognitifs principaux nous permettant de conceptualiser les objets mathématiques sont les métaphores et ce qu’on appelle le « mélange » (blending) conceptuel11.

7Il est intéressant de constater que la source de ces métaphores est l’expérience corporelle. Pour donner un exemple qui est devenu classique, selon Lakoff et Núñez le concept d’« ensemble » est compris par le biais de la métaphore du « Schéma-conteneur» (Container-schema) : un ensemble est considéré comme un récipient parce que comme un récipient il possède un intérieur, une limite et un extérieur, et les éléments de son intérieur sont reconnus comme les éléments de l’ensemble. Les auteurs affirment que celle-ci est une métaphore fondamentale, souvent seulement implicite, utilisée pour conceptualiser la notion mathématique d’ensemble telle qu’elle est déterminée par les axiomes de Zermelo-Fraenkel avec l’axiome du choix (ZFC).

8Cette interprétation de l’EM que nous avons qualifiée de « conceptuelle » a malheureusement certaines limites, qui ont été mises en évidence d’une manière très efficace par Schlimm dans un article récent12. Il faut préciser que Schlimm n’est pas en désaccord avec l’approche générale de Lakoff et Núñez, c’est-à-dire avec l’idée qu’il faudrait partir des sciences cognitives pour arriver à une analyse des idées mathématiques. Au contraire, il insiste sur le fait — positif — que Lakoff et Núñez ont été les premiers à chercher à bâtir finalement une théorie de la cognition mathématique qui ne s’intéresse pas seulement à l’arithmétique, comme d’autres nombreuses études de l’époque relatives aux bases cognitives des mathématiques13, mais aussi aux mathématiques avancées. Cependant, selon Schlimm, cette théorie devrait être discutée aussi d’un point de vue qui prend plus sérieusement en considération la pratique mathématique et son histoire. Pour revenir à l’exemple des ensembles, Lakoff et Núñez soutiennent qu’il existe une notion intuitive pré-mathématique de classe qui est « généralement » et « normalement » conceptualisée comme schéma-conteneur ; ce schéma serait donc notre métaphore naturelle, ordinaire et inconsciente de ce qui compte pour nous comme classe. Effectivement, dit Schlimm, la métaphore des ensembles comme conteneurs peut être retrouvée dans les premières pages d’un certain nombre de manuels d’introduction à la théorie des ensembles, mais seulement pour être après très rapidement abandonnée. Des analyses plus attentives ont révélé des défauts cruciaux dans ces métaphores14 et on découvre que la pratique mathématique est caractérisée par un aller-retour de différentes activités intellectuelles, dont la métaphore, mais pas seulement. Une idée peut être bien sûr suggérée par une vague métaphore, ainsi que par une intuition, ou par une caractéristique accidentelle de la notation qui a été choisie (comme on le verra, ce dernier point sera pour nous crucial). Pour arriver à des élaborations ultérieures, il faut de nouveaux essais et erreurs, voire aussi l’interaction avec d’autres mathématiciens, qui nous amènent à d’autres métaphores ou à d’autres notations plus sophistiquées, et ainsi de suite.

9Par conséquent, du point de vue d’une philosophie de la pratique mathématique, il faudrait une analyse plus nuancée des processus cognitifs qui sont impliqués par la pratique mathématique que celle que nous offrent Lakoff et Núñez ; par exemple, il faudrait faire une distinction entre les mathématiques des manuels et celles de la recherche, surtout quand notre sujet d’étude est marqué par certains développements historiques cruciaux tels que la définition de la notion d’ensemble dans la théorie des ensembles. Ce que Schlimm suggère est d’aller regarder ce qui en partie a été déjà réalisé pour la physique15, c’est-à-dire de chercher à atteindre à une science cognitive des mathématiques qui soit informée par l’histoire des mathématiques et inversement à une histoire cognitive des mathématiques telles qu’elles sont pratiquées en réalité.

10L’interprétation conceptuelle de l’EM semble donc être d’un côté trop limitée (il faut prendre en compte davantage qu’une activité intellectuelle quand on parle de conceptualisation en mathématiques) et de l’autre trop vaste (tous les concepts mathématiques ne sont pas « embodied » par le biais des métaphores fondamentales). Pour ces raisons, nous proposons de considérer une deuxième interprétation de l’EM, l’interprétation sémiotique,qui sera l’objet de la section suivante. Dans cette interprétation, l’approche de l’EM soutient plus simplement que les mathématiques comprennent des outils cognitifs qu’il faut percevoir et qui s’offrent comme un espace pour nos actions ; dans ce cadre, il se peut que des considérations sensori-motrices deviennent pertinentes. Cette interprétation semble donner un sens plus précis au rôle du corps dans la cognition mathématique, sans se concentrer sur la définition d’un seul mécanisme « embodied » tel que les métaphores fondamentales ou le mélange conceptuel, et nous permettra d’arriver à traiter la question de l’utilisation de l’imagination en mathématiques.

2. L’interprétation sémiotique de l’EM : notations, diagrammes et imagination manipulatoire

11L’approche sémiotique des mathématiques se propose d’étudier les facteurs sensori-moteurs qui peuvent influencer le raisonnement mathématique à partir des actions qu’on peut faire dans et sur les outils cognitifs qui font partie de chaque pratique mathématique. Dans cette section, nous présenterons et discuterons deux cas où cette influence nous semble évidente.

12Le premier cas concerne une série d’études accomplies par Landy et Goldstone16. L’objectif des expérimentateurs était d’évaluer comment en mathématiques la disposition physique des signes graphiques peut affecter la segmentation de simples équations. La segmentation correcte d’une certaine forme notationnelle dans ses composants formels est une partie délicate et en même temps routinière du raisonnement mathématique. Pour donner un exemple, une équation contenant des multiplications et des additions doit être décomposée d’une manière permettant d’effectuer les multiplications avant les additions. Les théories classiques du raisonnement mathématique semblent suggérer que cette segmentation est exécutée tout simplement en appliquant certaines règles formelles aux symboles notationnels individuels, cela conduisant à la supposition, comme l’affirment les auteurs, « appealing and tempting » que le sujet cognitif qui effectue cette segmentation extrait de façon triviale des notations physiques certaines séquences abstraites des symboles. Pour évaluer cette hypothèse, les expérimentateurs ont créé des formules qui expriment certaines équations dont les participants doivent juger la validité et leur ont ajouté une série de repères visuels, par exemple des espaces, des lignes, ou des cercles, leur hypothèse étant que ces repères influenceraient l’application des mécanismes de regroupement perceptifs, et par conséquent la capacité de raisonnement symbolique des participants (voir Fig. 1).

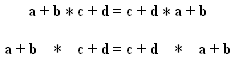
(fig. 1) Un exemple de manipulation où on ajoute des espaces entre les deux composants à multiplier (le regroupement visuel ne correspond pas à l’ordre de priorité des opérateurs)

13Effectivement, les résultats montrent que les jugements sur la validité des équations sont plus susceptibles d’être corrects si les regroupements visuels correspondent à l’ordre de priorité des opérateurs, c’est-à-dire quand par exemple un cercle est ajouté autour des éléments qu’il faut multiplier et non autour de ceux qu’il faut additionner. Dans un papier plus récent17, cette expérience a été reprise avec d’autres résultats similaires pour supporter celle que les auteurs appellent la « Théorie des Manipulations Perceptives » (Perceptual Manipulations Theory), qui soutient que la plus grande partie du raisonnement symbolique émerge de la façon dont les formalismes notationnels sont perçus et manipulés ; les notations servent de cibles pour l’activation des puissants systèmes perceptifs et sensori-moteurs. Cela montrerait que les gens utilisent des informations non formelles qui sont typiquement disponibles pour leur perception quand ils effectuent la segmentation de l’équation, intégrant cette information avec d’autres propriétés formelles.

14D’autres chercheurs ont proposé de parler d’« apprentissage perceptif » (perceptual learning) pour les mathématiques aussi, qui amènerait à des progrès dans la capacité d’extraire l’information pertinente de certaines notations formelles en vertu de l’expérience acquise18. Leur suggestion est de former les étudiants à reconnaître des expressions algébriques en utilisant des techniques standard d’apprentissage perceptif ; cela conduirait à des améliorations durables dans la lecture et la compréhension des équations ainsi que dans la résolution de problèmes en algèbre. Ils proposent donc de penser en termes de « modules d’apprentissage perceptifs » (perceptual learning modules), qui définissent les processus de découverte et de sélection de l’information et qui sont communs à la fois à certaines simples tâches sensorielles et à d’autres tâches cognitives plus complexes et même symboliques.

15Nous soulignons en passant que ces approches sont compatibles avec une hypothèse que nous avons faite récemment selon laquelle les êtres humains possèdent la capacité de « schématiser » et qui leur permettrait de relier différents systèmes cognitifs, déjà disponibles dans d’autres contextes tels que la perception ou l’action, mais avec un but spécifiquement inférentiel. Cette capacité se déclenche par le biais d’un outil cognitif matériel extérieur tel qu’une formule ou un diagramme, avec un objectif spécifiquement inférentiel, et elle serait à la base de l’introduction de ces outils19.

16Dans des travaux précédents en collaboration avec De Toffoli20, nous avons considéré le rôle des visualisations et plus généralement, des notations dans la pratique de la topologie. En particulier, nous avons proposé que les diagrammes utilisés dans la théorie des nœuds sont des outils dynamiques, c’est-à-dire qu’ils ne sont pas considérés par les experts comme des illustrations statiques mais s’offrent comme des instruments cognitifs pour imaginer les transformations qu’il serait possible d’effectuer sur eux-mêmes et en même temps — dans un sens que nous allons clarifier — sur les nœuds en tant qu’objets abstraits auxquels ils renvoient. Ces outils sont donc l’occasion pour une forme spécifique d’imagination manipulatoire de se déclencher : un expert en topologie doit apprendre comment (imaginer d’) effectuer certaines actions sur les diagrammes, pour explorer les propriétés inconnues des nœuds qu’ils étudient. Évidemment, ces actions sont des actions qui sont considérées comme légitimes à l’intérieur de la pratique, c’est-à-dire qu’elles sont des actions permises par la pratique.21 Pour clarifier, le théorème de Reidemeister stipule que deux entrelacs orientés sont isotopes si et seulement si nous pouvons passer de l’un à l’autre par une suite finie d’un des trois mouvements qu’on appelle de Reidemeister. Ces mouvements sont définis d’une manière graphique, à partir de gros plans sur les parties concernées d’un diagramme de nœud par chacun de ces trois mouvements22.

17Si on reprend donc les deux exemples des formules des équations et des diagrammes de nœud, l’interprétation sémiotique de l’EM nous semble être caractérisée par une idée principale et deux directions de recherche possibles. L’idée est que l’utilisation de certains outils cognitifs — une notation particulière, des diagrammes ou plus généralement une forme d’écriture au sens large — a une influence sur certains aspects de la conceptualisation en mathématiques. Le novice ainsi que l’expert perçoivent et agissent sur ces outils et, si l’on considère nos deux exemples, nous voyons comment cela peut amener à :

18(i) des effets non intentionnels des considérations sensori-motrices sur la conceptualisation qui deviennent une source possible d’« artéfacts » (au sens ici d’erreurs) induits par la notation ;

19(ii) des effets intentionnels des considérations sensori-motrices sur la conceptualisation.

20Il nous semble que dans tous ces cas les outils cognitifs de ce genre sont des « stimulateurs d’imaginaire ». Dans certains cas, cela peut être négatif, comme nous l’avons vu avec les résultats relatifs aux effets sur la performance dus à la manipulation des formules des équations ; dans d’autres cas, cela peut être en revanche positif, comme nous l’avons vu dans le cas des diagrammes de nœud. Il s’agit peut-être d’une question de « bon design » : si une notation ou plus généralement une certaine forme d’écriture est « bien conçue » (designed), alors elle servira de stimulateur d’imagination d’une manière efficace parce que l’imagination qu’elle déclenche est cohérente avec les contraintes, les buts et le cadre général de la pratique en question.

3. Comment peut-on caractériser l’imagination manipulatoire ?

21Admettons donc qu’il existe quelque chose comme l’imagination manipulatoire en mathématiques. Comment pouvons-nous la caractériser ? De quelle façon pouvons-nous concevoir les outils cognitifs utilisés en mathématiques comme des stimulateurs d’imagination ?

22Une stratégie possible pour répondre à ces questions est de nous référer à la théorie de l’art de Walton, qui se base sur l’imagination en tant que « faire-semblant » (make-believe)23. Cependant, nous montrerons pourquoi la seule théorie de Walton n’est pas suffisante mais peut être efficacement intégrée par une extension de la notion de « potentialité » (affordance) originairement introduite par Gibson dans sa psychologie écologique24.

3.1. « Faire-semblant » en mathématiques

23Walton a proposé de baser sa conception de l’art et de la fiction sur la notion de « faire-semblant ». Pour clarifier de quoi il s’agit, pensons à des enfants qui jouent avec des poupées ou des camions jouets (peu importe leur genre). Selon Walton, les poupées et les camions jouets servent de « supports » (props) dans des jeux de « faire-semblant » (pour réutiliser un terme que nous avons utilisé plus haut pour les outils cognitifs en mathématiques, ils sont eux aussi des stimulateurs d’imaginaire). Si l’enfant imagine que la poupée est un bébé réel, c’est effectivement sur la base de ce qui arrive à la poupée qu’il ou elle imagine en même temps plusieurs choses qui arriveraient au bébé. Bien sûr il existe des règles qui prescrivent ce que les enfants peuvent imaginer à partir de ces supports, que Walton appelle les principes de génération. Ces principes sont normatifs : ce qu’on peut imaginer dans le jeu est fictionnel mais il peut bien être vrai ou faux à l’intérieur de la fiction.

24Certains auteurs ont proposé d’utiliser la théorie de Walton dans le contexte des sciences naturelles. Par exemple, Toon a proposé une théorie de modèles en chimie basée sur le faire-semblant25. Selon l’auteur, les modèles aussi sont pour les scientifiques des « supports »dans des jeux de faire-semblant, tels que les poupées ou les camions jouets pour les jeux des enfants : les chimistes imaginent que les modèles sont des molécules presque de la même façon que les enfants imaginent qu’une poupée est un bébé ; de plus, les scientifiques peuvent s’imaginer eux-mêmes en train de voir et manipuler les molécules, donc ils « participent » à la modélisation de la même façon que les enfants participent à leur jeu de faire semblant. En chimie aussi les principes de génération sont des règles normatives : l’étudiant sait qu’il ne peut pas mal interpréter le modèle26. Un avantage d’une lecture waltonienne de l’utilisation des modèles en chimie est qu’elle se montre particulièrement efficace pour répondre aux problèmes ontologiques posés par la modélisation théorique ou mieux pour les faire disparaître.

25Revenons donc au cas des mathématiques. Les outils cognitifs en mathématiques tels qu’une formule ou un diagramme peuvent-ils être considérés comme supports eux aussi pour l’imagination manipulatoire ? Faisons ici un parallèle avec ce que Toon nous dit pour ce qui concerne les modèles en chimie. D’abord, les mathématiciens aussi imaginent que les diagrammes de nœud sont les nœuds mêmes, presque de la même façon que les enfants imaginent qu’une poupée est un bébé ; cela se montre bien dans l’ambiguïté du terme « nœud » qu’ils utilisent pour parler du nœud en tant qu’objet abstrait ainsi que du nœud en tant que diagramme de nœud. De plus, les mathématiciens peuvent s’imaginer en train de voir et manipuler les nœuds, et parfois même « vivre » dans l’espace topologique représenté, et cela témoignerait de leur « participation » dans la schématisation. Nous pouvons bien sûr faire l’hypothèse que ce type d’imagination peut avoir une base tout simplement spatiale, comme le montrent certains cas des mathématiciens aveugles qui ont produit des résultats très intéressants en topologie (voir le cas du mathématicien français Bernard Morin). Même dans le cas des mathématiques, nous pouvons penser en termes de principes de génération qui font partie de la pratique et sont des règles normatives : les mathématiciens savent qu’ils ne peuvent pas mal interpréter le diagramme, et les transformations qu’ils choisissent d’effectuer ou d’imaginer effectuer sont des actions autorisées par la pratique. De nouveau, cette approche peut être intéressante pour gérer un grand nombre de problèmes ontologiques, par exemple en suggérant d’aller vers une théorie fonctionnaliste des objets mathématiques27.

26Jusqu’ici, la théorie de Walton s’appliquerait donc bien au cas de l’imagination manipulatoire. Mais cette application de la théorie semble présenter deux problèmes principaux. Le premier problème peut être selon nous facilement surmonté. Par contre, le deuxième mérite d’être considéré sérieusement et nous amènera à réfléchir sur la possibilité d’intégrer cette théorie avec des éléments nouveaux qui seront abordés dans la section suivante.

27Pour ce qui concerne le premier problème, cette approche semble être très efficace pour le cas des représentations telles que les diagrammes de nœud mais moins naturelle pour expliquer le fonctionnement d’autres outils cognitifs tels qu’une formule. Cependant, nous proposons que l’imagination manipulatoire se déclenche même si les outils cognitifs utilisés ne sont pas iconiques. On peut penser qu’un expert en algèbre qui perçoit et agit sur une formule utilise la formule comme support pour imaginer manipuler des relations algébriques abstraites de la même manière qu’un expert en topologie utilise un diagramme de nœud pour imaginer manipuler le nœud abstrait. Quoique plus sophistiqué, il s’agirait quand même d’un jeu de faire semblant. Ceci nous permettra de donner une explication unifiée au rôle des outils cognitifs dans les mathématiques. Dans cette interprétation, le premier problème est ainsi surmonté.

28Un deuxième problème est par contre constitué par la définition de la détermination des principes de génération en mathématiques. Dans le cas de l’art, Walton soutient que ces principes sont fixés par certaines conventions et certaines contraintes culturelles. Que dire des mathématiques ? Dans la section suivante, nous chercherons à répondre à cette question.

3.2. Des règles extérieures aux potentialités

29Pour comprendre comment les principes de génération se définissent en mathématiques, nous allons nous référer à certaines approches propres aux sciences cognitives.

30D’abord, nous allons considérer le travail de certains auteurs qui se sont intéressés aux tâches cognitives dites « distribuées »28. Selon ces auteurs, un grand nombre de tâches cognitives demande le traitement des informations qui sont distribuées entre un esprit interne et un environnement externe. Dans leur interprétation, le système représentationnel de ce genre de tâches cognitives distribuées résulte d’un ensemble de représentations internes et externes, qui prises ensemble représentent la structure abstraite de la tâche29. Selon leurs résultats, plus les règles sont « distribuées » dans la représentation externe, plus facile devient le problème ; c’est-à-dire, quand les objets externes utilisés présentent des contraintes qui influencent le comportement de l’agent cognitif d’une manière telle qu’il est amené vers la solution du problème, les participants font moins d’erreurs. En fait, selon les auteurs, beaucoup d’erreurs sont dues à une surcharge de la mémoire de travail. Pour cette raison, il faut éviter que ces erreurs « internes » à l’esprit se produisent ; une solution est d’intégrer certaines règles dans les objets mêmes qui sont partie de l’environnement externe. Les règles extérieures seraient donc « intégrées » dans l’outil matériel et externe, c’est-à-dire qu’elles sont disponibles à la perception ou sont constituées par des contraintes physiques.

31Les outils cognitifs en mathématiques peuvent-ils incarner des règles extérieures de ce genre ? Le parallèle est évident : les mathématiciens agissent sur les outils cognitifs qu’ils ont à leur disposition. Pour clarifier, revenons à l’exemple des diagrammes de nœud : ces diagrammes sont bien conçus comme des outils cognitifs précisément parce qu’ils présentent certaines contraintes physiques qui induisent les experts à effectuer certaines transformations et pas d’autres, en ligne avec le but du jeu mathématique de faire semblant pertinent. Cependant, la reconnaissance de ces règles extérieures dépend de l’interprétation correcte des contraintes physiques et spatiales de l’outil cognitif à partir de la connaissance nécessaire d’arrière-plan : toutes choses étant égales par ailleurs, devant un même diagramme de nœud, un expert et un novice réagiront, se comporteront, imagineront des transformations d’une manière probablement très différente. Il nous semble donc que les contraintes physiques des outils cognitifs sont un élément nécessaire mais non suffisant pour expliquer leur utilisation.

32Plus généralement, l’approche de ces auteurs présente deux difficultés majeures. La première est constituée par leur distinction nette entre esprit interne et environnement externe. En fait, il nous paraît difficile de pouvoir distinguer si clairement entre ces deux éléments dans le cas des tâches mathématiques, et peut-être même dans tous les cas de tâches cognitives dites distribuées. En ligne avec l’interprétation sémiotique de l’EM, nous soutenons qu’il y a un aller-retour continu entre la conceptualisation de certains problèmes et la notation utilisée pour les aborder : la conceptualisation est influencée par la manière dont le problème est (re)présenté et en même temps la notation doit être correctement interprétée pour être comprise et utilisée de manière correcte. La deuxième difficulté est que leur exemple de tâche distribuée — le casse-tête de la tour d’Hanoi — comporte l’utilisation d’objets concrets extérieurs. Cependant, notre intérêt est de considérer des objets — tels qu’une formule physique — qui sont bien concrets mais qui, dans le contexte approprié, sont interprétés comme représentations, c’est-à-dire qu’ils sont des signes qui renvoient à d’autres objets plus abstraits.

33Heureusement, ces auteurs-mêmes nous offrent une voie de sortie à ce problème, qui mérite d’être d’explorée plus en détails. Quand ils définissent ce qui compte comme règle extérieure, ils se réfèrent brièvement aux « potentialités » (affordances) que les règles extérieures semblent fournir, reprenant un terme introduit par Gibson30. Dans la prochaine section, nous présenterons rapidement la notion de « potentialité » et nous discuterons comment une certaine extension de cette notion peut être utilisée pour intégrer le cadre waltonien et aboutir à une caractérisation satisfaisante de l’imagination manipulatoire en mathématiques.

3.3. Les potentialités représentationnelles

34Dans cette section, nous rappellerons très rapidement à quoi se réfère le terme « potentialité » introduit par Gibson. Ensuite, nous discuterons comment il est possible d’étendre cette notion au cas des outils cognitifs mathématiques.

35D’abord, il faut souligner que la psychologie écologique soutenue par Gibson avait comme présupposé précisément de défendre un refus d’une séparation nette entre sujet cognitif et environnement. Gibson introduit ainsi la notion de « potentialité »31 : les potentialités de l’environnement sont ce que l’environnement offre à l’animal, dans un sens qui peut bien être positif dans certains cas et négatif dans d’autres. Par exemple, si une surface possède les propriétés d’être horizontale, plate, étendue et rigide, alors elle « offre » (affords) un support. Malgré le fait que les propriétés d’une surface qui s’« offre » comme support sont physiques et par conséquent peuvent être mesurées en utilisant les échelles et les unités standard propres à la physique, les « potentialités » en tant que telles se mesurent relativement à l’animal. L’aspect intéressant de la notion de potentialité est en fait qu’elle se réfère en même temps à l’environnement et à l’animal, et laisse entendre la complémentarité des deux. Le fait que quelque chose dans l’environnement puisse s’offrir au corps et par conséquent au comportement de l’animal suggère que la frontière entre environnement et animal n’est pas fixée au niveau de la peau de l’animal mais peut au contraire se déplacer. Selon Gibson, quand on considère les potentialités, on échappe en définitive à la dichotomie philosophique et trompeuse basée sur une dualité absolue entre « objectif » d’un côté et « subjectif » de l’autre.

36Comment cette théorie peut-elle être utile pour parler du fonctionnement des outils cognitifs en mathématiques et de l’imagination manipulatoire ? Notre idée est de généraliser la notion de potentialité aux outils cognitifs. Evidemment, ces outils ne font pas partie de l’environnement de la même manière qu’une surface horizontale, plate, étendue et rigide. En fait, ces outils sont représentationnels, c’est-à-dire qu’ils font bien partie de l’environnement mais leur but est de se référer à des objets abstraits. Nous voulons donc introduire la notion de « potentialité représentationnelle » (representational affordance), c’est-à-dire la manière dont certaines notations, certaines écritures, ou certains diagrammes s’« offrent » comme terrain pour effectuer sur eux certaines actions. Si l’outil est bien conçu, alors ces actions permettront à l’expert de faire des inférences correctes et éventuellement d’apprendre quelque chose de nouveau sur les objets auxquels ces outils se réfèrent. Le fait que ces outils existent et sont introduits représente un avantage pour plusieurs raisons, dont deux sont les plus importantes. D’abord, l’utilisation de ces objets permet de décharger la mémoire de travail. En plus, ces objets présentent des potentialités représentationnelles grâce auxquelles ils peuvent servir comme cibles pour déclencher des capacités qui sont déjà familières à l’utilisateur, parce qu’elles ont été développées à l’occasion de ses rencontres avec le monde concret — perception et action, par exemple. Cela permet d’activer l’imagination manipulatoire et ainsi de considérer ces objets à la fois comme des objets concrets présents dans l’environnement et comme des signes pour d’autres objets plus abstraits dont on veut explorer les propriétés.

4. Conclusion : les potentialités représentationnelles pour faire semblant

37Dans cette dernière section, nous allons discuter de la possibilité de fournir une caractérisation de l’imagination manipulatoire en mathématiques dans un cadre waltonien intégré par la notion de potentialité représentationnelle dérivée de la notion gibsonienne de potentialité.

38Nous avons dit que les outils cognitifs sont des « stimulateurs d’imaginaire » : les experts les utilisent pour imaginer les conséquences épistémiques sur les objets dont ces outils sont signes de certaines transformations et manipulations. Comment cela est-il possible ? Et comment les principes de génération sont-ils déterminés dans ces jeux de faire semblant mathématiques ? C’est ici que nous proposons d’introduire les potentialités représentationnelles. Les outils cognitifs tels qu’une suite de signes dans une formule ou un diagramme de nœud possèdent, relativement à l’expertise de l’utilisateur, certaines potentialités représentationnelles, qui une fois reconnues et appliquées, vont aboutir à des résultats forcément corrects par rapport à la connaissance d’arrière-plan. Si l’outil est bien conçu, il s’offre à nos actions de manipulation d’une manière qui permet d’un côté de décharger la mémoire de travail et de l’autre de déclencher chez l’utilisateur son imagination manipulatoire. C’est à cet effet que l’outil a été spécialement conçu, en tant qu’instrument pour la découverte des nouvelles propriétés de l’objet représenté.

39Résumons donc notre parcours. Nous avons souligné l’intérêt de considérer les approches de l’EM qui critiquent les images standard de la cognition ainsi que des mathématiques comme totalement indépendantes des compétences plus basiques des êtres humains telles que par exemple la perception et l’action. Ensuite, nous avons discuté des limites de l’interprétation conceptuelle de l’EM et des avantages méthodologiques de prendre en compte une interprétation sémiotique de l’EM qui s’occupe de la manière dont on perçoit et agit sur certains outils cognitifs tels qu’une certaine notation ou certains diagrammes. Enfin, nous avons proposé que ces outils cognitifs sont des « stimulateurs d’imaginaire », c’est-à-dire des « supports » pour une forme d’imagination que nous avons définie comme « manipulatoire » parce qu’elle reprend certains éléments de notre perception et de notre action sur les objets ordinaires du monde concret. À travers cette forme d’imagination, on fait semblant de manipuler et de transformer des objets abstraits par le biais des manipulations et des transformations qu’on effectue sur ces outils. Pour définir ces actions, nous avons enfin introduit les potentialités représentationnelles qu’un expert est capable de reconnaître dans les propriétés physiques de ces outils.

40Ce cadre général nous semble rendre compte des exemples que nous avons présentés plus en haut. Les suites des signes d’une formule ainsi que les diagrammes utilisés en topologie présentent certaines « potentialités » pour l’expert et ces potentialités sont utilisées pour faire semblant de manipuler certains objets abstraits auxquels ils se réfèrent. Il faut souligner certains avantages de ce cadre walton-gibsonnien. D’abord, on dépasse une distinction trop nette entre esprit du sujet cognitif d’un côté et environnement matériel de l’autre. En outre, on se réfère aux objets représentés par les outils cognitifs utilisés comme des objets abstraits dont cependant il n’y a aucune raison de présupposer une quelconque forme d’existence. Cela nous permettrait de dépasser aussi une position ontologiquement problématique comme celle du platonisme.

41Il reste encore beaucoup à préciser. Par exemple, il nous semble important d’arriver à distinguer entre potentialités représentationnelles qui dérivent des capacités très spontanées telles que l’application des mécanismes de regroupement perceptifs, et d’autres qui nécessitent par contre une expertise plus sophistiquée. Cela sera l’objet d’un travail ultérieur.

Bibliographie

Voetnoten

Om dit artikel te citeren:

Over : Valeria Giardino