Jean Mawhin

Éloge de Jaroslav Kurzweil, membre associé de la Classe des Sciences

Résumé

Éloge de Jaroslav Kurzweil, décédé le 17 mars 2022. Mathématicien, auteur de contributions majeures sur les équations différentielles ordinaires et la théorie de l’intégration, il a été professeur et chercheur à l’Institut de Mathématiques de l’Académie des Sciences et à l’Université Charles à Prague.

Abstract

Eulogy of Jaroslav Kurzweil, dies on March 17, 2022. Mathematician, author of important contributions on ordinary differential equations and the theory of integral, he was professor and researcher at the Institute of Mathematics of the Academy of Science and at Charles University in Prague.

Jaroslav Kurzweil (1926-2022)

1Notre confrère Jaroslav Kurzweil est décédé le 17 mars 2022 à Prague, où il était né le 7 mai 1926. Il était âgé de 95 ans. Élu membre associé de la Classe des Sciences le 6 janvier 1996, il était devenu membre associé émérite le 18 décembre 2013. Il a participé à la séance de la Classe le samedi 31 mars 2007.

Signant le Livre d’or de l’Académie royale de Belgique, en présence de Léo Houziaux, 2007

2Les médias ont la regrettable habitude de privilégier l’image du mathématicien excentrique, voire du mathématicien fou. Jaroslav Kurzweil échappe définitivement à ces images. D’apparence tout à fait discrète, d’une simplicité et d’une modestie extrêmes, il trouvait son bonheur dans son pays d’origine, dans sa famille, parmi ses amis et ses collaborateurs, qu’il retrouvait avec plaisir dans un café, un restaurant ou une balade en forêt. Il appréciait en leur compagnie le vin blanc de Moravie et la bière de Pilsen. François Hollande l’aurait sans doute qualifié de « mathématicien normal ».

3Si on excepte des séjours de recherche en Pologne (1953), en URSS (1957), en Grande-Bretagne (1968-69) et en Belgique (1998), notre confrère a passé toute sa vie à Prague, ce qui ne l’a pas empêché d’être citoyen de deux nations, la Tchécoslovaquie et la Tchéquie, et de connaître trois régimes politiques. Il a toujours professé son opposition aux systèmes totalitaires.

4En 1945, la Seconde Guerre mondiale l’empêche de passer, au gymnasium de Prague-Schminov, les examens finaux, remplacés par la collecte des pommes de terre. Cela ne l’empêche pas d’étudier les mathématiques à l’Université Charles de Prague et d’obtenir, en 1949, son diplôme et un poste d’assistant à l’Université technique de la capitale. Un an plus tard, il décroche le titre de Rerum naturalium doctor avec une dissertation sur la théorie métrique des approximations diophantines, un domaine de la théorie des nombres qui mesure les ensembles de nombres réels jouissant d’une forme donnée d’approximation par des nombres rationnels. Ses seuls articles dans le domaine paraissent en 1951 et 1955, et le second résout par la négative une question posée par le célèbre mathématicien polonais Hugo Steinhaus.

5Chercheur depuis 1951 au futur Institut de Mathématiques de l’Académie des Sciences, Jaroslav Kurzweil est le premier docteur en mathématiques tchécoslovaque envoyé en séjour de recherche en Pologne. En 1953, il travaille trois mois à Poznan sous la direction de Wladislaw Orlicz, célèbre par les espaces de fonctions qui portent aujourd’hui son nom. Notre confrère étend aux applications entre espaces de Banach, qui généralisent l’espace usuel aux dimensions infinies, un théorème classique de Bernstein sur la caractérisation des fonctions analytiques réelles. Il donne également des conditions pour qu’on puisse approcher uniformément un opérateur continu entre espaces de Banach par des opérateurs analytiques. Ces résultats, dans un domaine sur lequel notre confrère ne reviendra plus, n’ont pas cessé d’inspirer de nouvelles recherches.

6Une autre conséquence de son séjour en Pologne a une immense importance dans sa vie : il y rencontre Stefania, née en 1928, qu’il épouse en 1956. Elle est décédée en 2018, deux ans après leurs noces de diamant.

Avec son épouse Stefania, Lliblice, 1996

7La vie familiale compte beaucoup pour notre confrère. Lors du congrès organisé à Prague pour ses 90 ans, son petit-fils veillait sur lui avec une sollicitude sans faille.

Avec son petit-fils, Prague 2016

8En 1954, Jaroslav Kurzweil est nommé chef du département d’équations différentielles ordinaires, un domaine alors peu étudié en Tchécoslovaquie. Il justifie aussitôt la confiance mise en lui en créant un séminaire hebdomadaire très suivi qui existe encore, et en apportant des contributions essentielles à la théorie de la stabilité au sens de Lyapounov. Une position d’équilibre d’un système mécanique dont les forces dérivent d’un potentiel V est stable lorsque V y atteint un minimum local strict. Au début du XX^e siècle, Alexandre Lyapounov a étendu ce résultat à un système général d’équations différentielles du premier ordre admettant un équilibre. Ce dernier est stable s’il existe une fonction réelle V nulle à l’équilibre, strictement positive dans son voisinage, et telle que V(x(t)) décroît pour t > 0 le long des solutions x(t) voisines de l’équilibre en t = 0. L’existence d’une telle fonction V, dite de Lyapounov, est donc une condition suffisante de stabilité. Savoir si cette condition est nécessaire est un problème difficile. Entre 1955 et 1957, Jaroslav Kurzweil apporte à cette question, pour différents types de stabilité, des réponses positives devenues classiques. Après un séjour de recherche de trois mois à Moscou en 1957, notre confrère est promu Docteur en Sciences, l’équivalent de l’habilitation, en 1958.

9Un autre domaine d’intérêt de Jaroslav Kurzweil est la méthode de centrage qui remonte à la théorie des perturbations en mécanique céleste aux XVIII^e et XIX^e siècles. Sa justification se ramène à montrer, pour un système d’équations différentielles de la forme x’(t) = f(t,x(t)), la dépendance continue des solutions dans un intervalle [a,b] par rapport au second membre des équations, à partir de conditions de continuité sur ce second membre f(t,x) et sur son intégrale indéfinie F(t,x) par rapport à t. En 1957, Jaroslav Kurzweil cherche à exprimer ces conditions en termes de F(t,x) uniquement. Cela le conduit à introduire un concept d’intégrale à partir de fonctions U(t,s) définies pour t et s appartenant à [a,b], en utilisant des sommes de Riemann de la forme [U(t₁,s₁) – U(t₁,s₀)] + [U(t₂,s₂) – U(t₂,s₁)] + … + [U(t_m,s_m) – U(t_m,s_m-1)] associées à des divisions a = s₀ < s₁ < s₂ < … < s_m-1 < s_m = b de l’intervalle [a,b] et à des t_k contenus dans [s_k-1,s_k] pour 1 ≤ k ≤ m. Le cas particulier où U(t,s) = f(t)s redonne les sommes de Riemann usuelles f(t₁)(s₁–s₀) + f(t₂)(s₂-s₁) + … + f(t_m)(s_m-s_m-1). L’intégrale classique de Riemann s’obtient en passant à la limite dans les sommes correspondantes lorsque tous les pas s_k-s_k-1 des divisions tendent vers zéro.

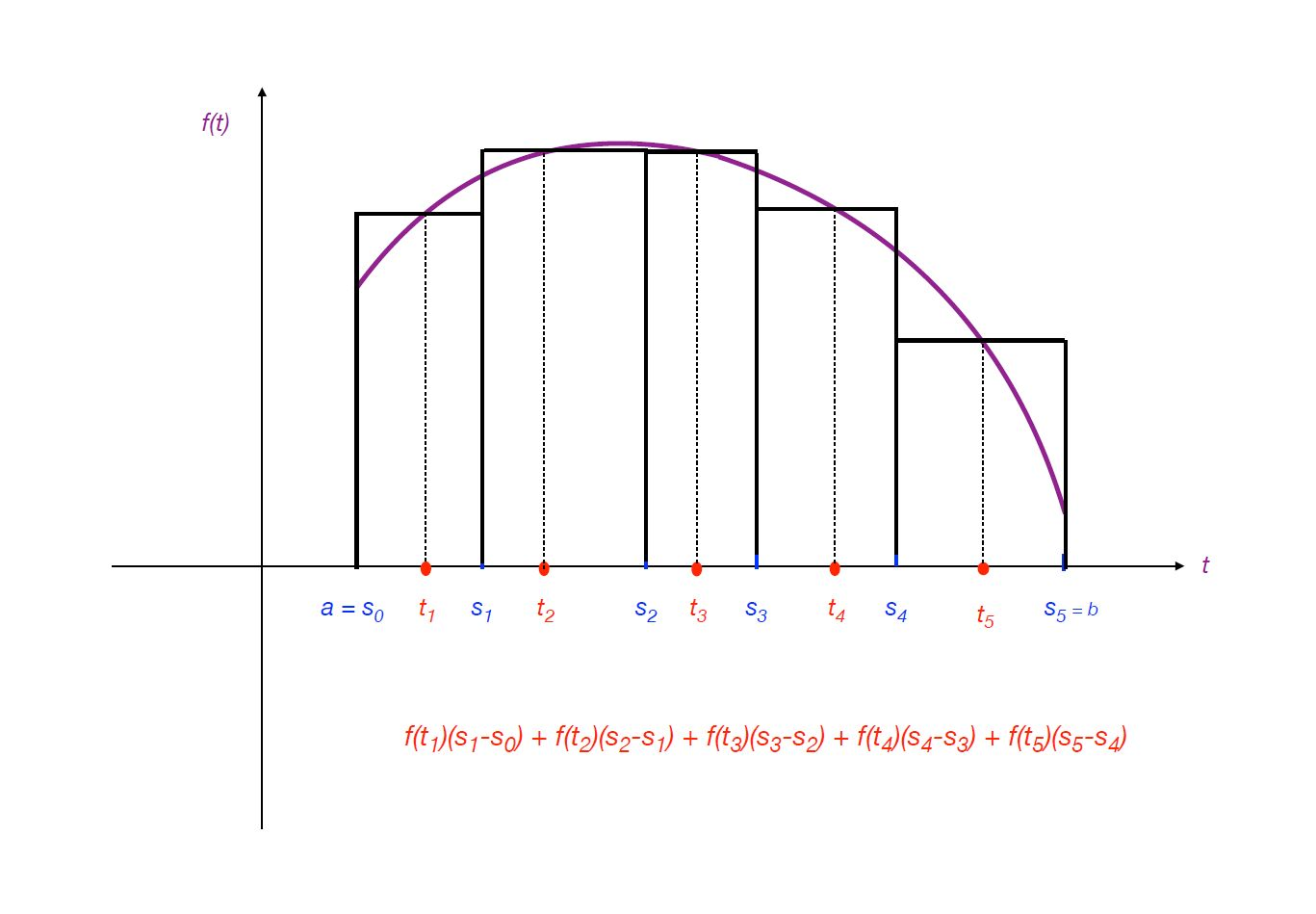
Somme de Riemann et intégrale

10Le même processus appliqué aux sommes de Riemann associées à U conduit à une intégrale insuffisante pour justifier la méthode du centrage dans le cas important où U(t,s) oscille avec une grande fréquence et une amplitude importante par rapport à t. En fait, le passage à la limite dans l’approche de Riemann ne tient pas compte de la nature de la fonction intégrée : les pas tendent vers zéro de la même manière pour toutes les fonctions. En termes de confection, ce passage à la limite est du type « prêt à porter » : c’est au client de s’adapter à un costume fait d’avance. Kurzweil a l’idée d’introduire un mode de passage à la limite « sur mesure » : les divisions autorisées doivent s’adapter à la fonction intégrée, en imposant à s_k-s_k-1 d’être d’autant plus petit que la variation de la fonction est rapide et violente entre s_k-1 et s_k. Ce but est atteint par une modification formellement mineure de la définition de Riemann. Kurzweil définit ainsi une intégrale suffisamment puissante pour conduire, lorsqu’elle est appliquée à la fonction U(t,s) = F(s,x(t)), à des équations différentielles généralisées, dont les solutions ne sont plus nécessairement continues. Ces équations contiennent comme cas particuliers les équations différentielles ordinaires, les équations intégrales de Volterra, les équations différentielles comprenant des retards, des impulsions ou des mesures et les équations aux différences. L’efficacité et l’actualité de cette approche sont illustrées par la parution, l’an dernier, d’un ouvrage de plus de 500 pages rédigé par un groupe de mathématiciens brésiliens dirigés par Marciá Federson.

11Dans son article fondateur de 1957, Jaroslav Kurzweil a montré que l’intégrale ainsi définie est équivalente, lorsque U(t,s) = f(t)s, à celle introduite en 1915 par Oskar Perron, par une approche moins géométrique et moins intuitive. Cette intégrale de Perron intègre toutes les dérivées et généralise celle introduite en 1900 par Henri Lebesgue, à laquelle elle se réduit lorsqu’on impose à la valeur absolue de f d’être également intégrable. Enfouie dans un article substantiel consacré aux équations différentielles, la définition de Kurzweil passe inaperçue en dehors de Prague, au point d’être redécouverte indépendamment en 1961, à partir de considérations entièrement différentes, par Ralph Henstock, professeur à Coleraine (Irlande du Nord) et spécialiste de l’intégrale. Une telle double paternité n’est pas rare en mathématiques. Elle n’a engendré aucune querelle de priorité, comme celle restée célèbre entre Newton et Leibniz pour le calcul infinitésimal. Les relations entre Kurzweil et Henstock ont toujours été cordiales, à l’image de leurs rencontres à Coleraine en 1988, pour les 65 ans de Henstock, et à Prague en 1996, pour les 70 ans de Kurzweil.

Rencontre avec Ralph Henstock, Coleraine 1988

12Depuis longtemps, le cours commun de calcul différentiel et intégral destiné aux futurs ingénieurs, mathématiciens et physiciens de l’Université de Louvain, développait l’intégrale de Riemann, bien adaptée au public et au nombre d’heures allouées. Lorsqu’on sépara en 1976 les étudiants de sciences appliquées de ceux de la faculté des sciences, on augmenta pour ces derniers le nombre d’heures afin de remplacer l’intégrale de Riemann par celle de Lebesgue, indispensable aux mathématiciens et physiciens théoriciens. Les approches classiques de l’intégrale de Lebesgue me semblaient trop difficiles pour des étudiants de première année, et je trouvais peu pédagogique d’introduire l’intégrale de Riemann en première pour la remplacer en seconde par celle de Lebesgue. Je portais mon choix sur la définition riemannienne de Kurzweil et Henstock, qui levait ces difficultés. J’y suis resté fidèle jusqu’à l’éméritat et j’ai eu le plaisir de voir mes successeurs confirmer ce choix.

13L’Université de Louvain, pionnière dans cette innovation pédagogique, a été suivie par un nombre croissant d’institutions partout dans le monde, et les manuels qui l’exposent se comptent aujourd’hui par dizaines. En 2007, Jaroslav Kurzweil, invité à Louvain-la-Neuve pour le cinquantenaire de son intégrale, accepta gentiment de faire aux étudiants de première année en mathématiques et physique, spontanément rejoints par ceux des années suivantes, un exposé sur l’origine d’une intégrale qui les avaient fait rêver ou souffrir. Mes tentatives pour renouveler l’expérience avec Newton, Leibniz, Euler ou Cauchy sont restées désespérément vaines.

Un cours à Louvain-la-Neuve, 2007

14Au niveau de la recherche, ce renouveau de l’approche riemannienne s’est montré fécond dans l’étude des intégrales stochastiques, des mathématiques financières et dans la justification des mystérieuses intégrales de Feynman en mécanique quantique.

15Les travaux de Jaroslav Kurzweil sur les équations différentielles généralisées l’ont conduit, dans les années 1960, à étudier les variétés intégrales de systèmes différentiels, pour lesquelles toute solution issue de la variété pour un t₀ y reste quel que soit t. Le problème principal consiste à trouver des conditions pour que les perturbations suffisamment petites de systèmes différentiels possédant une variété intégrale conservent la même propriété. Notre confrère l’a résolu sous des hypothèses si générales que ses résultats s’appliquent à des équations différentielles à retard et à des équations aux dérivées partielles, et que des cas particuliers ont été régulièrement redécouverts par d’autres dans les années suivantes.

16En 1966, Jaroslav Kurzweil ajoute à ses fonctions à l’Institut de Mathématiques de l’Académie celle de professeur ordinaire à l’Université Charles de Prague. Son enseignement donne naissance en 1986 à son remarquable traité Ordinary Differential Equations.

17Notre confrère a également perçu l’importance croissante de la théorie du contrôle optimal, dans laquelle les systèmes différentiels dépendent d’une fonction supplémentaire dont on dispose pour imposer aux solutions un comportement donné. Cette théorie conduit à une autre généralisation de la notion d’équation différentielle, les inclusions ou relations différentielles, dans lesquelles f(t,x) est, pour chaque t et x, un ensemble (multifonction) et la dérivée x’(t) de la solution est assujettie à appartenir à l’ensemble f(t,x(t)) pour chaque valeur de t. Un des résultats obtenus par Kurzweil, en collaboration avec Jiri Jarnik, autour de 1980, porte sur l’approximation de f(t,x) par des multifonctions plus régulières.

18Jusqu’au début des années 1980, et contrairement à son alter ego Henstock, Kurzweil a peu contribué à sa théorie de l’intégration, si on excepte la publication en 1980 de la monographie Nichtabsolut konvergente Integrale, qui étend l’intégrale à des fonctions de plusieurs variables à valeurs dans un espace de Banach, ce qui ne pose pas de difficultés particulières. En 1981, j’ai réalisé que cette intégrale n’intègre pas la divergence d’un champ de vecteurs simplement différentiable sur un pavé (produit de n intervalles), dès que n ≥ 2. J’ai proposé en 1981 une intégrale plus générale redonnant, sous ces hypothèses minimales, le théorème de la divergence. Dans cette généralisation, on restreint encore plus les divisions du pavé en sous-pavés dans les sommes de Riemann en contrôlant la régularité de ces sous-pavés, c’est-à-dire le rapport entre leur plus long et leur plus court côté. Cette intégrale conserve la plupart des propriétés de celle de Kurzweil-Henstock à une notable exception près : l’intégrabilité sur chaque morceau d’un pavé coupé en deux n’entraîne plus l’intégrabilité sur le pavé entier. Le plus grand mérite de ce travail fut sans doute de réveiller l’intérêt de Jaroslav Kurzweil pour la théorie de l’intégrale, comme il l’a reconnu lui-même en me dédicaçant l’ouvrage mentionné plus haut.

19Avec ses collaborateurs de Prague, Jaroslav Kurzweil montre en 1983 comment remédier au défaut d’additivité en utilisant une notion plus globale, quoique moins géométrique, de la régularité. Ensuite, avec Jiri Jarnik, il remplace le pavé par un ensemble bordé par une variété en utilisant des divisions basées sur des partitions de l’unité, ce qui lui permet de prouver une formule de changement de variables. Jusqu’en 1997, il développe de nouveaux types d’intégrales riemanniennes à partitions régulières et les compare à celles introduites par d’autres mathématiciens, dont son compatriote Washek Pfeffer, professeur à Davis (Californie).

20À la fin des années 1990, Jaroslav Kurzweil revient aux intégrales en dimension un et discute la structure de l’espace des fonctions intégrables correspondantes. Ce problème d’analyse fonctionnelle, beaucoup plus délicat que pour l’intégrale de Lebesgue, est abordé dans deux notes publiées dans feu notre Bulletin de la Classe des Sciences en 1997 et 1998. Notre confrère les développe dans deux livres Henstock-Kurzweil integration: its relation to topological vector spaces et Integration between the Lebesgue integral and the Henstock-Kurzweil integral: its relation to locally convex vector spaces, publiés en 2000 et 2002, qui révèlent une fois de plus son immense virtuosité technique. Son dernier ouvrage Generalized ordinary differential equations: not absolutely continuous solutions, paru en 2012, donne une présentation d’ensemble actualisée des équations différentielles généralisées, confirmant qu’en mathématiques aussi, on revient souvent à ses premières amours.

21Une carrière scientifique aussi riche et une personnalité aussi attachante ne pouvaient pas échapper aux honneurs, que notre confrère ne rechercha jamais. Malgré son peu de sympathie pour le régime communiste et l’emploi de son autorité scientifique et de la force tranquille de son caractère pour aider des collègues menacés par ce régime. Jaroslav Kurzweil reçut le Prix d’État Klement Gottwald en 1964 et la médaille d’argent Bernard Bolzano en 1981. La fin du communisme se traduisit par une pluie de médailles décernées par Président de la République, l’Académie des Sciences, et l’Université Charles, par le Prix Comenius en 1996, et la médaille Josef Hlavka en 2001. En 2006, Jaroslav Kurzweil fut lauréat du prestigieux prix Ceská hlava attribué annuellement depuis 2002, pour contributions exceptionnelles, à un intellectuel tchèque. Il est le seul mathématicien à l’avoir reçu.

22Notre confrère a été élu membre correspondant (1968) et membre effectif (1988) de l'Académie tchécoslovaque des Sciences, membre honoraire de la Société royale d’Édimbourg (1978), membre honoraire de l’Union des mathématiciens et physiciens tchécoslovaques (1987). Il est membre fondateur de la Société savante de Prague (1994) et docteur honoris causa de l’Académie slovaque des Sciences (1996), de l’Institut de Technologie de Brno (1999), de l’Université d’Opava (2001), de l’Université de Brno (2001) et de l’Université de Pilsen (2003).

23Jaroslav Kurzweil pratiquait avec art un humour typiquement slave, qui n’est pas étranger à l’atmosphère amicale qui régnait à l’Institut de Mathématiques, qu’il présida pendant de nombreuses années. Il savait donner à cet humour une couleur politique, sans avoir l’air d’y toucher. On se souvient que l’invasion soviétique de la Tchécoslovaquie de 1968 avait débuté le 21 août, et chaque année, les autorités communistes étaient assez nerveuses à l’approche de cette date. Le hasard voulut que la séance d’ouverture du congrès international Equadiff 7 de Prague se tienne le 21 août 1989. Notre confrère, président du congrès, commença son discours d’ouverture par les mots : « Aujourd’hui, nous célébrons un important anniversaire », avant de marquer un silence. Les auditeurs, en particulier ses compatriotes, retinrent leur souffle, et il poursuivit : « il y a deux cents ans aujourd’hui, naissait l’un des plus grands mathématiciens de tous les temps, Augustin Cauchy, pionnier de l’analyse mathématique ». Jaroslav Kurzweil remit le couvert lorsqu’il reçut le Prix Ceská Hlava. Dans son discours de remerciement, il insista sur le fait qu’en mathématiques, « ce qui était vrai hier est encore vrai aujourd’hui ». Cette remarque fut interprétée dans la presse comme un commentaire sur les difficultés politiques tchèques du moment. Elle traduisait peut-être le regard lucide mais toujours bienveillant de notre confrère sur la nature humaine.

24Car il était avant tout un sage ; pas un sage austère et puritain prêchant le salut par le renoncement, mais un sage qui construit son bonheur sur les petites joies. Lors d’un colloque organisé en 2008 dans un ancien couvent de Hejnice en Bohême, assis sur un banc du jardin en compagnie de mon épouse, Jaroslav savourait la paix du paysage, la lumière scintillante de l’automne et le chant des oiseaux avant leur grand départ. Quand mon épouse remarqua qu’on ne pouvait rien ajouter à ce bonheur, il répondit en souriant : « si, un verre de vin blanc ». Si le paradis existe, notre confrère mérite, par sa personnalité, sa vie et son œuvre, que les anges lui indiquent le chemin de la tonnelle la plus proche1.

Notes

Para citar este artículo

Acerca de: Jean Mawhin