Propagation function: towards constant time algorithms

Document(s) associé(s)

Annexes

• AS_13_n1_137_SCH (1,2M)

Abstract

Let P_n be the regular n-sided polygon inscribed in a circle of radius 1 in the plane. The distance from x to y induced by P_n is the smallest size of the homothety of P_n centered at x and containing y. On X, simply connected planar set, the propagation function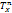is defined by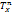(x) = sup_y∈_X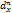(x,y) where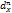(x,y) is the geodesic distance in X, that is the lower bound of the length (induced by P_n) of the paths entirely lying inside X and linking x to y. Efficient algorithms for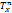are based on the following remark: the farthest points to any x in X may have only a few possible locations Y. In this paper, it is shown that, as in the convex case, there exists a set Y with at most n elements, such that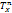(x) = sup_y∈_Y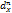(x,y). In the case of the square lattice equipped with the 4-connectivity distance, this theorem leads to an algorithm computing the propagation function by means of at most 7 geodesic balls, whatever the shape of X.

Pour citer cet article

A propos de : Michel Schmitt