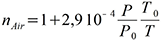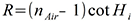Résumé

Entre le 23 janvier et le 12 février 1898, l’expédition d’Adrien de Gerlache en Antarctique a réalisé un important levé cartographique du Détroit de Gerlache entre le Cap Neyt à l’extrémité nord-est de l’Île de Liège et le Cap Renard en Terre de Danco. Son commandant en second, Georges Lecointe, officier de navigation et hydrographe, a effectué des observations astronomiques destinées à fixer les coordonnées de plusieurs stations qui ont servi de référence pour déterminer le tracé des lignes de côte. Dans cet article, nous tentons d’évaluer la précision et l’exactitude de ces mesures à la lueur de la documentation cartographique disponible actuellement. Nous exposons les limites de l’approche et les sources d’incertitudes relevant des méthodes utilisées à la fin du XIXe siècle et de nos interprétations pour restituer la position des stations sur les documents actuels. Les hypothèses explicatives majeures du biais constaté en longitude et latitude sont probablement une sous-estimation de la réfraction et des observations du soleil généralement matinales.

Abstract

Between January 23 and February 12, 1898, Adrien de Gerlache expedition in Antarctica carried out an important cartographic survey of the “de Gerlache Strait” between Cape Neyt at the north-eastern end of Liège Island and Cape Renard in the Terre de Danco. Its second in command, Georges Lecointe, navigation officer and hydrographer, carried out astronomical observations intended to fix the coordinates of several stations that were used as a reference to delineate coastlines. In this article, we attempt to assess the precision and accuracy of these measurements in the light of the cartographic documentation currently available. We expose the limits of the approach and the sources of uncertainties related to the methods used at the end of the 19th century and to our interpretations to restore the position of the stations on the current documents. The major explanatory hypotheses for the bias observed in longitude and latitude are probably an underestimation of refraction and observations of the sun generally in the morning.

Introduction

1On connaît la grande importance de l’Antarctique pour l’étude de l’évolution du climat ainsi que son rôle sur ses conséquences telle que hausse du niveau marin, par exemple (The IMBIE team, 2018 ; Dethinne et al., 2022). Par ailleurs, l’Antarctique est protégé jusque 2048 de toute exploitation minérale et d’hydrocarbures par le Protocole au Traité sur l’Antarctique relatif à la protection de l’environnement datant de 1991. Cependant, dans le contexte géopolitique actuel, le renouvellement de ce traité en 2048 fait déjà l’objet de discussions sur de futures activités minières (Zhang et Talalay, 2021). Aujourd’hui, la documentation cartographique sur l’Antarctique est riche et précise, notamment grâce à l’imagerie satellitaire (Williams et al., 1982 ; Lahaye, 2010 ; réf. Web 1, 2 et 3). Mais l’histoire de sa cartographie a commencé au crépuscule du XIXe siècle et la Belgique y a contribué d’une belle façon.

2Ainsi, l’expédition scientifique belge en Antarctique à bord de la Belgica commandée par Adrien de Gerlache a été un exploit remarquable. Le navire appareilla d’Anvers le 16 août 1897. Le 14 janvier 1898, après une traversée de l’Atlantique et un arrêt à Punta Arenas, il fait route vers les terres antarctiques. Le 23 janvier, il pénètre dans la baie de Hughes dont les contours ne sont pas exactement tracés sur les cartes. Les explorateurs croyaient d’abord entrer dans une baie sans issue, mais il apparut qu’un passage inattendu s’ouvrait entre les falaises et débouchait dans l’océan Pacifique.

3Le jour de la découverte de l’entrée du détroit, de Gerlache (de Gerlache de Gomery, 1902) écrit : «Le 27 février 1898, nous pénétrons dans un détroit que nous avons entrevu le 24 - orienté vers le Sud-Ouest - et dont la baie de Hughes forme, en quelque sorte, l’entrée septentrionale. Ce détroit n’est pas figuré sur les cartes, aussi éprouvons nous, à nous y engager, cette joie et cette émotion spéciales qui s’emparent des navigateurs lorsque l’étrave de leur navire laboure des flots vierges ».

4À propos de l’entrée de la Belgica dans ce passage, de Gerlache (de Gerlache de Gomery, 1902) écrit : « Nous sommes entourés de terres élevées ; dans la baie nous voyons plusieurs icebergs et quelques îles et îlots dont l’un, très dégagé de neige, attire particulièrement notre attention ; les cartes ne l’indiquant pas, je lui donnerai par la suite le nom de mon père et le baptiserai îlot Auguste ». Le navire séjourne trois semaines dans ce vaste bras de mer, d’abord appelé détroit de la Belgica, mais renommé détroit de Gerlache après le retour de l’expédition. Inlassablement, A. de Gerlache et G. Lecointe, commandant en second de l’expédition, officier de navigation et hydrographe, vont cartographier ce détroit jusqu’alors inexploré.

5R. Amundsen, second lieutenant, écrit le 27 janvier 1898 (Decleir, 1998), lorsque le navire se trouve au large de l’île Auguste : “The only thing we can say with certainty is that the old charts are wrong. The Hughes Bay where we were is now behind us. We have discovered a very large strait which extends in a (southwesterly) direction ...”. H. Arctowski (1901) écrit à ce sujet: “Captain Lecointe, assisted by Commander de Gerlache, was busy from morning till night on survey work, the Belgica being moved from place in order that all details of the coast might be seen from near at hand; Dr Cook was constantly at work taking photographs”.

6Les informations cartographiques disponibles avant l’expédition consistaient en deux documents de qualité discutable (de Gerlache de Gomery, 1901) : la Carte de l’Amirauté Anglaise (Figure 1) et la Carte de L. Frederichsen (Figure 2). La première est un vague tracé avec de nombreuses imprécisions. R. Amundsen (Decleir, 1998) écrit à son sujet : « The Admiralty chart appears to be very inaccurate so that we were uncertain of our position”. Concernant la seconde, de Gerlache (de Gerlache de Gomery, 1901) affirme : « La carte Petermann and Friederichsen, qui devrait reprendre les découvertes du Capitaine allemand Dallmnan, effectuée en 1873-1874, est complètement erronée ».

7Ainsi, conscient de l’importance du levé cartographique, de Gerlache mit tout en œuvre pour permettre à Lecointe de rassembler les données nécessaires malgré le fait que l’expédition poursuivait des buts scientifiques multiples et concurrents concernant leurs calendriers respectifs.

8Une nouvelle carte du détroit de Gerlache fut donc produite au terme de l’expédition belge.

9Dans cet article, nous proposons de valider l’hypothèse qu’il est possible de quantifier l’erreur affectant les coordonnées astronomiques de différentes stations calculées par Lecointe en 1898 (Lecointe, nd ; 1903a et 1903b) en les comparant aux coordonnées géodésiques actuelles de ces mêmes points positionnés sur les documents cartographiques récents.

10Cette comparaison a été faite en appliquant la méthode décrite dans la section I.

11Pour être en mesure de discuter de l’origine des différences mesurées, il est évidemment nécessaire de démontrer que nous disposons d’une information suffisante sur la façon dont Lecointe a effectué ses observations astronomiques et sur la façon dont il a réalisé ses calculs. La section II a pour objectif de répondre à cette exigence en qualifiant les données sur l’expédition de 1898 en notre possession.

12Par ailleurs, il est aussi important de valider les positions actuelles qui résultent d’une interprétation comparative visuelle des documents cartographiques produits par Lecointe et de l’information cartographique actuelle. Cette validation est décrite dans la section III.

13La section IV expose les résultats de la comparaison de coordonnées.

14Enfin, dans la section V, nous discutons les sources d’erreurs possibles au regard des méthodes mises en œuvre à l’époque et de l’évolution ultérieure des connaissances et techniques de la géodésie (Malys et al., 2015). Cette discussion montrera les limites de l’approche que nous avons adoptée et les précautions à prendre pour démontrer notre hypothèse initiale.

I. MéTHODE DE COMPARAISON DES COORDONNéES

15Nous avons analysé les coordonnées astronomiques calculées par Lecointe (1901a et nd) de onze stations principales réparties dans le détroit de Gerlache. Les coordonnées de neuf d’entre elles furent mesurées par observations astronomiques lors de débarquements (« stations à terre »), les deux autres ont été réalisées sur le navire (« stations à bord »).

16Pour évaluer l’incertitude de ces coordonnées, nous avons exploité les quelques brèves descriptions des sites de ces stations datant de l’expédition ainsi que leur report sur les « cartes » établies à cette époque. Leur position sur les cartes et dans les bases de données récentes de l’Antarctique a été interprétée au mieux, puis leurs coordonnées « actuelles » ont été estimées.

17Parmi les données cartographiques actuelles, citons deux sources cartographiques du British Antactic Survey (BAS) : les éditions de 2008 et 2017 d’une carte (BAS-UKAHT) de la Northern Antarctic Peninsula (réf. Web2) et la couche High resolution vector polylines of the Antarctic coastline de sa base de données géographiques (réf. Web3).

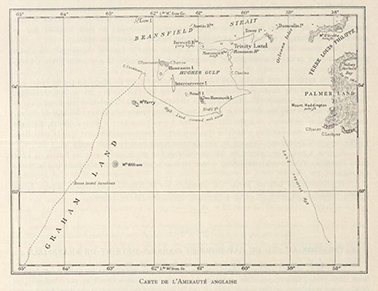
Figure 1. Reproduction en réduction de la Carte de l’Amirauté Anglaise (source : Lecointe, 1903b).

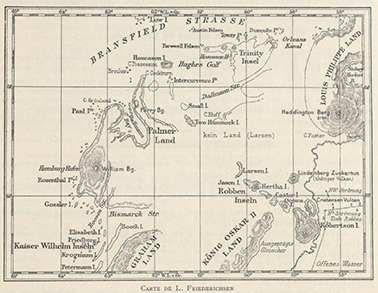
Figure 2. Reproduction en réduction de la carte de L. Friederichsen (1841-1915), géographe, cartographe et aussi éditeur allemand. Cette carte s’inspirait des découvertes par E. Dallmann (1830-1896), chasseur de baleines et explorateur allemand, de différentes îles et terres antarctiques entre 1873 et 1874. (source : Lecointe, 1903b).

18La version imprimée à l’échelle du 1 : 250000 de la carte du BAS utilisée est réalisée en projection cartographique Lambert Conforme Conique : parallèles standard sécants 64°40’S et 67°20’S, méridien central 63°W, système géodésique horizontal WGS84. Les données géographiques numériques du BAS sont, quant à elles, fournies en coordonnées stéréographiques polaires antarctiques calculées sur base du système géodésique horizontale WGS84 (EPSG3031).

19Deux autres sources ont été exploitées : la base de données d’images satellitaires LIMA (Landsat Image Mosaic of Antarctic) de l’USGS (Williams et al., 1982 ; Lahaye, 2010 ; Web 1) et Google Earth Pro (version 7.3.4.8573) qui, dans ces régions, met à disposition majoritairement de l’imagerie Landsat du projet LIMA et plus récente. Le trait de côte et la nature des côtes et terres émergées visibles sur les images constituent évidemment des éléments permettant d’interpréter la position « actuelle » la plus probable des stations levées par Lecointe. Par ailleurs, la qualité géométrique de ces produits est assurée par les nombreux points de contrôle mesurés au sol par GNSS pour corriger géométriquement les images et par l’exploitation de MNS autorisant, grâce au contrôle de la position et de l’assiette des plates-formes satellitaires, un géo-référencement direct.

20La position « actuelle » de chaque station a ainsi été déterminée, indépendamment par chacun des deux co-auteurs de cet article, sur la carte du BAS imprimée au 1 : 250000 (J.-J. Derwael), d’une part, et en exploitant, soit la base de données géographiques du BAS, soit les produits LIMA et Google Earth (Y. Cornet), d’autre part. La mesure des coordonnées géographiques a été réalisée sur chacune de ces sources. Elles ont ensuite été comparées aux coordonnées calculées pendant l’expédition de 1898 (Lecointe, nd et 1903a).

21Pour chaque station, les composantes est-ouest (Δx) et sud-nord (Δy) exprimées en m entre les coordonnées « actuelles » et les coordonnées de 1898 ont simplement été calculées en utilisant les formules suivantes :

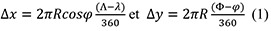
Avec	(λ, φ)	coordonnées géodésiques (WG84) “actuelles” exprimées en degrés,
	(Λ,Φ)	coordonnées calculées en 1898 par observations astronomiques exprimées en degrés,
	R	un rayon terrestre exprimé en m.

22Les deux composantes de l’erreur résultant de cette formule sont exprimées en mètres. Le couple (Δx, Δy) d’une station est un vecteur-erreur dont l’origine (0,0) correspond à la position « actuelle » et l’extrémité est la position calculée en 1898.

23Chaque vecteur-erreur a ensuite été reporté sur un même graphique bivarié des erreurs (Δx, Δy). Ce graphique permet de comparer l’erreur de localisation de toutes les stations. Il alimente la discussion de la section V. Mais, avant cette discussion et pour appréhender au mieux les sources d’erreurs et leur ordre de grandeur, il importe de décrire les données collectées sur l’expédition de 1898 (section II).

II. DONNéES sur L’EXPéDITION DE 1898

A. « Cartes » du Détroit de Gerlache

24Quatre documents cartographiques de cette région ont été établis (voir références cartographiques) : un croquis provisoire du détroit de la Belgica, un croquis provisoire du détroit de Gerlache, un levé rapide (Carte V. Expédition antarctique belge. Détroit de Gerlache) que nous nommons « carte finale » dans la suite de l’article, le Sketch of Danco Land, the Belgica Strait and Palmer Archipelago Surveyed. Il est important de noter que Lecointe emploie rarement le terme « carte » dans ses différents rapports, et jamais sur les représentations graphiques du détroit de Gerlache. D’ailleurs, il formule plusieurs avertissements concernant leurs imperfections (Lecointe, 1903a) liées à la courte durée du séjour dans le détroit avec une météo défavorable aux observations, l’absence de repères visibles et reconnaissables de loin, l’impossibilité d’observer les étoiles pendant l’été austral constituant un problème sérieux selon Loodts (1966) et une lune invisible. Il était uniquement prévu de faire un simple croquis de la région visitée et de l’étudier en détail l’année suivante. Plus de précision au levé représentait une perte de temps car la bonne saison était déjà fort avancée et d’autres observations scientifiques devaient être réalisées.

25Pendant l’expédition, Lecointe dresse le « croquis provisoire » en exploitant les observations astronomiques et les levés de traits de côtes effectués entre le 23 janvier et le 12 février 1898. Vingt débarquements permettront aux scientifiques d’explorer les terres dont neuf furent consacrés au calcul de coordonnées de « stations à terre » par observations astronomiques. Deux déterminations de coordonnées par observations astronomiques ont aussi été effectuées « à bord ». Les coordonnées géographiques de ces onze stations ont servi de points d’appui principaux pour le levé des côtes.

26De nombreuses descriptions des lieux visités, comme l’exemple suivant, se retrouvent dans les différents rapports : « Cap Neyt, au 53 S.W., l’île Low (?) à 20 miles environ au 18 N.E. et deux points remarquables d’une terre assez élevée l’un à 16 miles environ et au 64 N.E., l’autre à 12 miles environ au 75 N.E., le groupe Nord des îles Christiana entre le 79 et le 76 S.E. » (Lecointe, 1903a).

27Des photos ont été prises par F. Cook, médecin et photographe américain de l’expédition et de nombreux croquis furent exécutés (Figure 3). Ces derniers représentent la configuration des côtes aux endroits où des observations astronomiques furent exécutées. Ces documents constituent, avec les descriptions et particularités rapportées par les explorateurs, des informations essentielles pour interpréter les positions « actuelles » les plus probables.

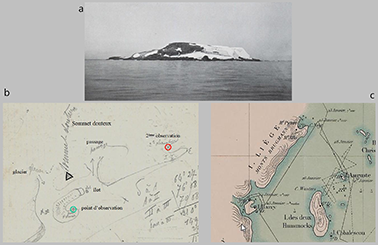
Figure 3. a. Photographie de l’Ile Auguste (23.01.1898). b. et c Région de l’Ile Harry et l’Ile de Liège (Cap Neyt) où furent réalisés les débarquements 4 et 5, respectivement le 25 janvier 1898 à 7 h 00 et à 13 h 45. b. Schémas annotés des côtes. c. Extrait de la « carte » finale (Lecointe, 1903b).

28Lecointe (1903a) décrit les méthodes qui ont été employées au cours de l’expédition pour le levé des côtes reportées sur ses « cartes ». Les points secondaires de la côte ont été relevés par des observations faites « à bord », le navire étant immobile ou en marche.

29Si le navire était immobile, la méthode des trois segments capables fixait sa position à condition que trois repères principaux aux coordonnées connues avec suffisamment de précision soient visibles et bien disposés. La vérification de cette condition semble très peu probable vu la distribution spatiale de ces repères, leur faible nombre et la météo défavorable. Ensuite, les angles horizontaux entre ces repères et les points secondaires ont été mesurés au sextant tenu horizontalement afin d’obtenir une série de lieux géométriques passant par chacun de ces points secondaires. Il fallait au moins deux arrêts du navire pour appliquer cette méthode.

30Si le navire était en marche, sa position était déterminée à l’aide de deux points (relèvements) ou de trois points (segments capables). Connaissant la route au compas et la vitesse, il était possible d’interpoler cette position pour un instant quelconque. Dans ces conditions, le relevé d’un même point à certains intervalles de temps était réalisé afin de positionner sur la carte les points secondaires de la côte par la méthode des recoupements.

31Les mesures des orientations au compas nécessitaient de connaître la déclinaison magnétique. E. Danco, physicien du globe, l’a déterminée à 20° 43’ 13’’ NE, le 3 février 1898 dans les Monts Solvay sur l’Ile du Brabant. Selon plusieurs sources (Jonkers et al., 2003 ; Web4 ; Web5), la déclinaison magnétique dans la région du détroit de Gerlache en 1900 était de l’ordre de 15°à 20° vers le NE. Tenant compte du fort gradient spatial de cette déclinaison, spécialement selon la direction suivie par la Belgica, le calcul de Danco peut être considéré cohérent par rapport aux modèles actuels de l’évolution du champ magnétique terrestre. Néanmoins, ce fort gradient aurait nécessité de la réévaluer à plusieurs endroits pendant le voyage. Il n’y a aucune trace de cela et il n’est pas précisé dans les différents rapports scientifiques de façon univoque le protocole de mesure des azimuts.

32Une autre méthode semble avoir été utilisée, la même mesure d’angles horizontaux au sextant et d’estimation de distances « à l’œil ». Connaissant les coordonnées géographiques de la station, celles du point visé était alors déterminées par la méthode « orientation et distance ». Outre la difficulté de relever, depuis le navire, un grand nombre de points des traits de côtes très découpées, l’estimation des distances est très incertaine. Cela a conduit à une généralisation excessive du tracé des côtes sur les « cartes » de 1898 car, au-delà d’une certaine distance, l’œil humain sous-estime fortement les variations de distance.

33Sur la carte V de l’annexe cartographique publiée par Lecointe (1903b,), ont été reportés : le parcours fléché et daté suivi par la Belgica, les débarquements, les sondages bathymétriques, des icebergs, des amas de glaces, des récifs, des glaciers et des « courbes de niveau » schématiques. Un nom a aussi été donné aux caps, montagnes, baies, îles et îlots (Verlinden, 2008).

34La Figure 4 montre un extrait du croquis provisoire dressé par Lecointe. La Figure 5 montre une reproduction en réduction de la « carte » finale sur laquelle nous avons symbolisé de façon lisible les stations dont les coordonnées ont été déterminées par observations astronomiques effectuées en 1898 et leurs positions “actuelles” (interprétation de Y. Cornet). Ces stations font l’objet de notre analyse en section III.

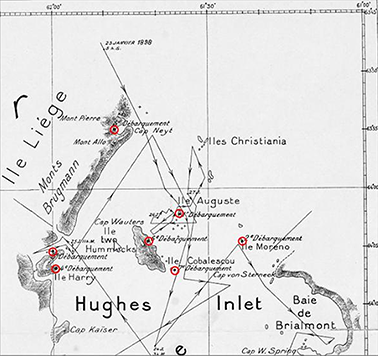
Figure 4. Extrait du “Croquis provisoire” dressé par Lecointe (disponible à la bibliothèque de l’Institut Royal Belge des Sciences Naturelles) avec le parcours fléché du navire ainsi que les dates et lieux des débarquements symbolisés en rouge par nos soins.

Figure 5. à gauche, reproduction en réduction de la carte du détroit de Gerlache (Lecointe, 1903b, carte V de l’annexe cartographique). à droite, la même région vue sous Google Earth. Les cercles représentent les positions des stations levées par observations astronomiques Lecointe (nd et 1903a). Les croix représentent les positions que nous avons déterminées (interprétation de Y. Cornet) en exploitant les ressources cartographiques actuelles. NE : Cap Neyt (25/01/1898), HA : Ile Harry (25/01/1898), AU : Ile Auguste (26-27/01/1898), CO : Ile Cobalescou (27/1/1898), LO : Ile Louise (30/01/1898), AN : Ile d’Anvers (8/02/1898), WI : Ile Wiencke (9/02/1898), WA : Iles Wauwermans (09/02/1898), MO : Ile Moureaux (11/02/1898), DA : Cap Renard sur la Terre de Danco (12/02/1898).

35Les dimensions de la « carte » finale sont 58x55 cm. Elle couvre la région située entre 63° 50’ et 65° 20’ S et entre 61° 00’ et 64° 20’ W-Greenwich. La zone couverte par le document a une étendue, en longitude, de ~163 km et, en latitude, de ~167 km. Il n’y a pas de mention concernant la projection cartographique, mais à l’analyse de l’aspect de la grille des méridiens et parallèles et du rapport des distances entre méridiens et entre parallèles qui est de l’ordre de 0,43, soit le ~cos 64°, il nous semble qu’il s’agit d’une projection équi-rectangulaire avec une latitude de référence de l’ordre de 64°S. Il s’agit aussi du rapport des longueurs d’une minute d’arc de parallèle et de méridien au milieu de la carte qui valent respectivement ~797 m et ~1 853 m. Nous avons estimé l’échelle de la carte à ~1 : 320 000. À cette échelle, l’erreur graphique (0,2 mm) correspond à une distance de 60 m.

B. Instruments utilisés par Lecointe pour réaliser les observations astronomiques

36La précision des coordonnées calculées en 1898 est intimement liée aux instruments utilisés à l’époque. Lecointe (1901a) décrit tous les instruments de mesure dont il dispose.

37Lors des observations astronomiques, les angles ont été mesurés au sextant construit par Hurlimann Paris (Figure 6A). Le rayon du segment du cercle gradué est de 19 cm et l’approximation de la lecture du vernier vaut 10’’. Il faut cependant tenir compte des erreurs systématiques et constantes ainsi que des conditions dans lesquelles les mesures sont effectuées. Selon Duhamel (1949), la précision moyenne du sextant serait de l’ordre de 1’. Un écart-type de 30’’ semble plausible. Lecointe (1903a) arrondit généralement les résultats de ses calculs de coordonnées géographiques à 15’’ près ou 1’ près selon les méthodes mises en œuvre (Tableaux 1 et 2).

Figure 6. a. Sextant Hurlimann Paris – 1895 (https://www.liveauctioneers.com/item/71303435_sextant-by-la-hurlimann-paris-c-1895) ; b. Horizon artificiel à miroir (Source : archives de la famille de Gerlache); c . Ne disposant pas de photos des instruments employés, nous montrons, à titre d’exemples, un chronomètre Carl Ranch (https://www.invaluable.com/auction-lot/carl-ranch-copenhagen-a-mahogany-marine-chronomet-683-c-a524febbf1).

38En mer, la mesure de la hauteur angulaire au sextant se fait à partir de l’horizon naturel ou ligne séparant la mer du ciel. Lorsque l’horizon naturel n’est pas visible et pour les observations sur terre, Lecointe utilise un horizon artificiel constitué d’une surface réfléchissante (liquide ou miroir) parfaitement immobile et horizontale. L’expédition disposait de deux horizons artificiels : le premier liquide (huile ou mercure contenu dans une cuvette) et le second formé d’un miroir rectangulaire porté par un cadre en métal (Figure 6B). Pour lever les coordonnées de “stations à terre”, l’utilisation de l’horizon artificiel et du sextant monté sur trépied constitue un élément favorisant une plus grande précision que celle obtenue par les pratiques marines de l’époque.

39Trois types de compas destinés à mesurer l’azimut magnétique ont aussi été emportés par l’expédition : un compas étalon du système Thomson, un compas liquide et quelques compas d’embarcation (Lecointe, 1901a). Ils auraient été utilisés pour déterminer le cap suivi par le navire et pour orienter des tours d’horizon au sextant.

40Concernant la mesure du temps, elle était essentielle pour le calcul de la longitude à la fin du XIXe siècle, soit une dizaine d’années avant la première utilisation des signaux horaires (Hutchinson, 1908). L’expédition disposait de cinq chronomètres (Figure 6C) : deux chronomètres Carl Ranch (Copenhague), les n° 501 et 564, respectivement nommés A et B par Lecointe (1901a et 1901b) ; un chronomètre (n° 1277) Charles Shepherd (Londres) ; une montre de torpilleur (n° 3263) Le Roy (Paris) et un chronomètre (n° 7844) Ulysse Nardin (Locle – CH). Pendant l’expédition, il semblerait que les deux chronomètres systématiquement utilisés sont les chronomètres Ranch. Tous nécessitaient un réglage régulier.

41Les méthodes citées par Lecointe (1901a) pour ce réglage sont : les éclipses des satellites de Jupiter, les occultations d’étoiles par la Lune, la méthode des distances lunaires. Mais sachant que les étoiles et la Lune n’étaient pas visibles pendant l’exploration du détroit de Gerlache, il y a de fortes chances que la précision de la mesure du temps ait été affectée d’une dérive (Remy, 1909) partiellement corrigée a posteriori par interpolation entre le 30/12/1897 et le 14/03/1898. La première date correspond au réglage par des hauteurs mesurées à l’horizon artificiel et, la seconde, au commencement de l’éclipse du premier satellite de Jupiter.

42Pendant la traversée du détroit de Gerlache, le temps absolu à midi Tmg (Temps moyen de Greenwich utilisé par Lecointe) a varié entre 00h 00m 15s.29 et 00h 00m 09s,17 et les marches diurnes en secondes entre 0 et -0,3, -2,8 et -3,0, +2,1 et +2,2 et +2,4 et +3,8 (Figure 7), respectivement pour les chronomètres A, B, C et D (Lecointe, 1901a). Lecointe (1901a et b) a appliqué la méthode de correction de la mesure du temps par les chronomètres en fonction de la température tel que suggérée par Mouchez en 1855 (Boistel, 2006). À titre indicatif, signalons que, selon Yvon-Villarceau (1875) cité par Boistel (2006), après une traversée de soixante-huit jours de mer, cinq chronomètres de marine n’ont pas dévié de plus de l’équivalent de six secondes d’arc, soit ~85 m à 64°S. Par ailleurs, les chronomètres de l’époque subissaient des variations brusques de marche sans cause apparente. Pour le reconnaître et éliminer les mesures affectées, Remy (1909) rappelle que 3 chronomètres étaient nécessaires. Une erreur de 10 secondes sur la mesure du temps à la latitude du détroit de Gerlache correspond à 1995 m d’erreur en longitude. L’erreur de mesure du temps par Lecointe est probablement bien inférieure à cette valeur de 10 secondes.

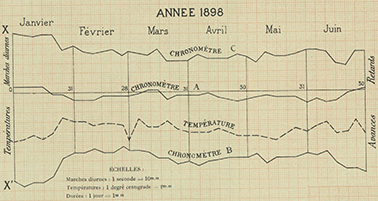
Figure 7. Marche diurne des chronomètres A, B et C et variation de la température pendant l’année 1898 (Lecointe, 1901b). Le chronomètre A montre les variations les plus faibles. Les chronomètres A et B sont généralement utilisés par Lecointe dans ses calculs (Lecointe, nd).

C. Méthodes de calcul des latitude et longitude adoptées par Lecointe

43La précision des coordonnées calculées en 1898 est aussi intimement liée aux méthodes de calcul de cette époque. Lecointe (1903a) décrit les différentes méthodes de détermination des latitudes et longitudes.

1. Correction des hauteurs angulaires

44La formule de calcul de la hauteur astrale vraie au-dessus de l’horizon est différente pour les observations « à bord » et « à terre » car celles effectuées « à bord » exploitent la surface de la mer comme horizon et celles effectuées « à terre » exploitent un horizon artificiel. La formule pour les observations « à bord » est :

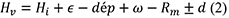
Avec	Hv	hauteur vraie du centre de l’astre,
	Hi	hauteur instrumentale, la valeur lue sur le sextant,
	ϵ	erreur instrumentale,
	dép	dépression,
	ω	parallaxe,
	Rm	réfraction moyenne,
	d	demi diamètre de l’astre.

45Notons que dans toutes les formules de l’article, nous utilisons les notations de Lecointe (1903a).La formule pour les observations « à terre » est :

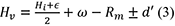
Avec

d’

demi diamètre de l’astre quand il s’agit du soleil ou de la lune.

2. Détermination directe de la latitude

46Trois méthodes sont décrites par Lecointe (1903a) : la hauteur méridienne du soleil, les circum-méridiennes et la hauteur de la culmination de la lune.

47Détaillons les deux premières étant donné que la lune n’était pas visible pendant l’exploration du détroit de Gerlache.

48La méthode de la hauteur méridienne du soleil repose sur la mesure précise de sa hauteur angulaire à sa culmination au passage dans le méridien du lieu et de l’heure exacte de ce passage. Elle permet de déterminer la latitude φ (notation de Lecointe, elle correspond à Φ de la formule de la section I) par l’addition algébrique de la distance zénithale et de la déclinaison de l’astre provenant des éphémérides :

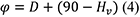
Avec	D	déclinaison solaire,
	(90°-Hv)	distance zénithale solaire.

49La méthode des circum-méridiennes consiste à observer le soleil avant et après son passage méridien. On traite chaque pointé séparément en amenant chaque observation de hauteur à ce qu’elle aurait été, si elle avait été effectuée à l’instant du passage méridien (réduction au méridien). La formule générale est l’expression d’une parabole :

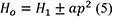
Avec	H0	hauteur de l’astre au moment de son passage au méridien,
	H1	hauteur vraie de l’astre au moment où l’angle au pôle était p,
	a	changement de hauteur de l’astre pendant la minute précédant ou suivant ce passage,
	p	angle au pôle.

3. Calcul de la longitude par la méthode de l’angle horaire

50Cette méthode consiste à comparer le Temps vrai de Greenwich (Tvg), au temps astral (solaire, car, dans le détroit de Gerlache, c’est le seul astre qui a été observé) local (Tal) :

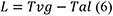
Avec

L

angle horaire assimilable à la longitude.

51Si plusieurs observations ont été réalisées sur un très court laps de temps, un calcul de longitude moyenne, Lm, est alors effectué à partir des différentes valeurs obtenues de L.

52Nous renvoyons le lecteur à Lecointe (1903a) pour les détails de calcul de Tvg à partir du temps mesuré avec les différents chronomètres réglés sur le temps moyen et, plus particulièrement les chronomètres Carl Ranch A (n° 501) et B (n° 564).

53Tal est estimé à partir de la hauteur astrale (solaire) vraie Hv, d’une estimation préalable de la latitude φ par une des méthodes précédentes et par la distance polaire Δ. Pour le soleil, Tal équivaut au Temps vrai local (Tvl).

54Dans le triangle sphérique construit sur les 3 côtés 90-Hv, 90-φ et Δ, il est possible d’estimer l’angle au pôle de l’astre observé par la formule des cosinus, mais, Lecointe (1903a) a utilisé une formule des demi-côtés car elle est plus adaptée à l’utilisation des tables de logarithmes :

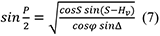
Avec	2S = φ + Hv + Δ

4. La méthode de Marcq St Hilaire

55La méthode de Marcq St Hilaire permet de construire une droite de hauteur. Dans ses notes manuscrites, Lecointe (nd) l’intitule « Calcul de la position (Méthode du point rapproché) ». Cette droite est la tangente au cercle de hauteur à proximité de la position estimée de l’observateur (Lecointe, 1903a). Elle est perpendiculaire à l’orthodromie joignant le point approché (φe, Le) et le point subsolaire (Figure 8a). Si plusieurs droites de hauteur peuvent être construites par l’observation d’un même astre à différents moments ou de différents astres à un « même » moment, le calcul de leurs intersections permet une estimation plus précise de la position. Dans le détroit de Gerlache, le soleil a été observé à différents moments.

56Le point subsolaire est estimé par la mesure du Temps moyen de Greenwich selon Lecointe (Tmg) donné par le chronomètre qui est ensuite corrigé de l’équation du temps (Em) lue par Lecointe dans les éphémérides pour obtenir le Temps astral local (Tal). L’angle du soleil au pôle (Pe) correspond à Tal. La déclinaison du soleil (D) est aussi calculée pour déterminer la latitude du point subsolaire. Nous renvoyons à Lecointe (nd ; 1903a) pour les détails des calculs.

57Les coordonnées de la position approchée et du point subsolaire déterminent un triangle sphérique avec le pôle terrestre. Sa résolution permet de calculer une hauteur solaire attendue (Hc) au point approché à l’instant de l’observation. La différence entre Hv du soleil découlant de la mesure au sextant au même moment et Hc donne l’intercept. Sa valeur permet de positionner la droite de hauteur sur l’orthodromie dont l’orientation est l’azimut géographique (Z) de l’astre depuis le point approché à cette heure. Z est calculé par la formule :

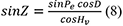
Avec	Z	azimut géographique du soleil dans le sens horaire à partir du nord géographique,
	D	déclinaison du soleil provenant des éphémérides,
	Hv	hauteur vraie du soleil,
	Pe	angle horaire du soleil.

58La Figure 8b illustre l’application de la méthode des droites de hauteur à la station de l’île Harry. Les droites de hauteur D1 et D2 sont construites depuis les deux points déterminatifs Z1 et Z2. L’intersection des deux droites de hauteur est le point Z cherché (attention, ici, Z1, Z2 et Z ne correspondent pas à des azimuts !).

Figure 8. a. Principe du dessin de la droite de hauteur. b. Exemple d’application de la méthode d’intersection entre deux des droites de hauteur à la station de l’île Harry par Lecointe (1903a).

59Avec un angle de 25° entre les droites D1 et D2 et avec l’intercept de la seconde mesure valant 20’’ (distance Z1Z2), on détermine la distance x :

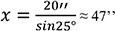
60en direction de 24° sud-est (azimut de 156°, 66°+90°)

61Une troisième méthode, la méthode directe, est décrite par Lecointe (1903a) pour fixer une position. Cependant, elle ne concerne aucune des stations faisant l’objet de notre analyse.

62Le Tableau 1 détaille les méthodes utilisées en 1898 pour chaque station.

Station	Date-heure (1898)	Méthode (1)	Température °C	Pression atm. mm Hg	Réfractation	Azimut	Horizon	R calculé (2) en f(P,T) Arc seconde	DeltaR Arc seconde
NE	25 janvier 3h du soir	Droite de hauteur HV1 : 35°00’50,2’’ HV2 : 34°55’20,2’’ HV3 : 34°40’05,2’’ HV4 : 34°35’40,2’’	5	746,0	1’23,2’’	58°03’30’’ NW	Artificiel	85,89	-2,69
HA	25 janvier vers 8h du matin	Droite de hauteur HV1 : 31°39’18,85’’ HV2 : 31°45’38,85’’ HV3 : 31°56’48,85’’ HV4 : 32°08’38,85’’	5	746,0	1’34,9’’	65°54’ NE	Artificiel	96,59	-1,69
	25 janvier vers 9h50 du matin	Droite de hauteur HV1 : 39°40’32,3’’ HV2 : 39°47’27,3’’ HV3 : 39°53’57,3’’	5	746,0	1’10,5’’	41°11’15’’ NE	Artificiel	71,78	-1,28
AU	26 janvier vers midi	Méridienne HV1 : 44°32’38’’	1	744,0	1’01’’	~0° NE	Artificiel	61,55	-0,55
	27 janvier vers 6h45 du matin	Droite de hauteur HV1 : 20°46’35’’ HV2 : 20°56’00’’ HV3 : 21°01’45’’ HV4 : 21°13’35’’	1	742,0	2’36,5’’	~90° NE	Artificiel	157,13	-0,63
CO	27 janvier vers midi	Méridienne à bord HV1 : 44°10’54’’	1	742,0	1’00’’	~0°	Mer	62,24	-2,24
LO	30 janvier vers 8h du matin	Droite de hauteur HV1 : 27°36’53,3’’ HV2 : 27°45’36,3’’ HV3 : 28°05’01,3’’ HV4 : 28°30’46,3’’	1	735,0	1’57’’	71°16’ NE	Artificiel	112,21	4,79
AN	8 février vers midi	Circum-méridienne HV1 : 40°17’17,30’’	5	746,0	1’08’’	~0° NE	Artificiel	70,48	-2,48
WI	9 février vers 7h15 du matin	Angle horaire HV1 : 21°18’11’’ HV2 : 21°24’46’’ HV3 : 21°30’56’’ HV4 : 21°37’21’’	6	746,5	2’31’’	~90° NE	Artificiel	151,45	-0,45
WA	9 février vers midi	Méridienne HV1 : 39°35’59’’	3	749,0	1’12’’	~0°	Artificiel	73,33	-1,33
MO	11 février vers 9h du matin	Angle horaire HV1 : 31°02’34,5’’ HV2 : 31°08’54,5’’ HV3 : 31°35’44,5’’ HV4 : 31°41’14,5’’	0	756,0	1’41,7’’	~30°NE	Artificiel	101,05	0,65
DA	12 février vers 10h45	Angle horaire HV1 : 37°03’03,4’’ HV2 : 37°06’03,4’’ HV3 : 37°10’33,4’’ HV4 : 37°12’38,4’’	0	753,0	1’19,6’’	~35°	Artificiel	81,14	-1,54
	12 février vers midi	Méridienne HV1 : 38°29’41’’	2	753,0	1’16’’	~0°	Artificiel	76,76	-0,76

Tableau 1. Méthodes de calcul de la position des stations principales.

(1) Droite de hauteur = méthode du point rapproché (Lecointe, nd et 1903a).

(2) Calculs effectués par nos soins en utilisant les équations suivantes proposées par Dufour (2001) :

Avec n_Air Indice de réfraction de l’air,

P Pression atmosphérique en Pa,

P_o Pression atmosphérique de référence (101325 Pa),

To Température de référence de l’air (288.15 K),

T Température de l’air en K,

R Valeur angulaire de la réfraction,

H_i Hauteur instrumentale de l’astre observé.

(3) Delta R = différence entre la réfraction calculée par Lecointe (nd et 1903a) et celle obtenue par les formules ci-dessus.

III. POSITIONS DES STATIONS SUR LES DOCUMENTS CARTOGRAPHIQUES ACTUELS

63Le procédé de levé des côtes en 1898 a produit un tracé très généralisé, mais il est relativement conforme au tracé détaillé des données cartographiques et des images satellitaires actuelles. Ainsi, certaines stations ont pu être localisées de façon assez certaine sur les documents actuels. Par contre, nous avons éprouvé beaucoup plus de difficultés à en localiser d’autres (Figure 9).

Figure 9. Exemples de localisations interprétées de 6 stations principales sur les documents cartographiques actuels. à gauche, 6 positions sur la « carte » de 1898. À droite, les positions homologues dans Google Earth (imagerie Landsat principalement). 1. HA ; 2. MO ; 3. NE ; 4. LO ; 5. AN ; 6. WI. Les stations HA, MO et NE sont des exemples de stations positionnées avec une bonne certitude sur les documents actuels. Les positions « actuelles » de LO, AN et WI sont des exemples plus incertains.

A. Localisations « actuelles » les plus certaines

64Les positions de 5 stations ont été interprétées sur les documents actuels avec une précision très satisfaisante. De la plus précise à la moins précise, citons : l’île Auguste, l’île Harry, l’île Cobalescou, les îles Moureaux et le Cap Neyt.

1. Île Auguste (AU)

65La station de l’île Auguste a été localisée à l’aide de la base de données vecteur du BAS au centre de l’île. L’incertitude en longitude et en latitude est d’une centaine de mètres.

2. Île Harry (HA)

66Lecointe localise la station de l’île Harry sur son cap sud-oriental. Sur les documents cartographiques actuels, ce cap apparaît avec une forme différente. Par ailleurs, les coordonnées calculées par Lecointe ne correspondent pas à la position reportée sur sa carte. Nous estimons l’incertitude de localisation « actuelle » à quelques centaines de mètres en longitude et latitude. L’impact sur l’orientation du vecteur-erreur peut être important étant donné la proximité de la position calculée par Lecointe et la position « actuelle ».

3. Île Cobalescou (CO)

67Bien que l’île Cobalescou soit une « station à bord » considérée moins fiable par Lecointe, nous l’avons prise en compte dans notre analyse. Son positionnement sur les documents actuels ne pose pas de problème particulier. Même s’il s’agit d’une « station à bord », notre choix de position sur les documents actuels est au centre de l’île. Elle est affectée d’une incertitude de l’ordre de quelques centaines de mètres en longitude et en latitude.

4. Îles Moureaux (MO)

68La station des îles Moureaux a été positionnée entre les deux îles. Ces deux îles sont disposées selon un axe WNW-ESE. L’incertitude de notre interprétation est au maximum de l’ordre de 400 m en longitude et 200 m en latitude.

5. Cap Neyt (NE)

69Sur la « carte » de 1898, la baie du Cap Neyt où Lecointe a localisé la station montre un tracé homologue sur les documents actuels. Nous y avons positionné la station en un lieu homologue sur les documents actuels. Mais une incertitude persiste car Lecointe décrit « le fond d’une petite baie à l’ouest du Cap Neyt ». L’endroit que nous avons choisi n’est pas une petite baie. Par ailleurs, le fond de la baie est occupé par un front glaciaire avec des crevasses et séracs peu propice au débarquement. On imagine mieux un débarquement sur une partie de côte rocheuse visible de part et d’autre de la baie. Une position actuelle sur un de ces promontoires rocheux produirait un vecteur-erreur très différemment orienté de celui obtenu en utilisant le fond de la baie. L’incertitude de notre interprétation est de l’ordre de 800 m en longitude et en latitude.

B. Localisations « actuelles » les plus incertaines

1. Île Louise (LO)

70Lecointe (1903b) positionne la station de l’île Louise sur la côte septentrionale du cap Anna loin à l’ouest de l’Île Louise, alors qu’il décrit le débarquement sur les récifs de l’île Louise. Il y a donc un doute important sur sa position exacte. Le report des coordonnées calculées par Lecointe positionne la station près et au nord-est de l’Île Louise. L’incertitude existe mais nous estimons avoir retrouvé la position homologue sur les documents actuels avec une assez bonne fiabilité.

2. Île d’Anvers (AN)

71La côte sud de l’île d’Anvers est vraiment très généralisée sur la « carte » de Lecointe. Cela rend l’interprétation d’une position sur les documents actuels très incertaine. La distance par rapport aux îles se trouvant au sud-ouest (cap Hippolyte) et la présence sur la « carte » de Lecointe d’une ondulation de la côte séparant deux golfes au tracé beaucoup plus généralisé que sur les documents actuels permet de proposer une localisation « actuelle » de la station avec une incertitude de 2000 à 3000 m en longitude et de 1500 m en latitude.

3. Île Wiencke (WI)

72Le tracé de la côte septentrionale de l’île Wiencke est lui aussi très généralisé sur la « carte » de 1898. Des ondulations du tracé semblent correspondre à la succession de 3 proéminences visibles sur les documents actuels, mais l’aspect de la côte sur les documents actuels diffère assez fortement de celui de la « carte » de Lecointe. Il semblerait que la station de l’île de Wiencke soit située où se trouve actuellement Port Lockroy. Cette interprétation est néanmoins très incertaine surtout en latitude.

4. Cap Renard sur la Terre de Danco (DA)

73Pour la station du cap Renard sur la Terre de Danco, le même type de problème d’interprétation que pour les stations des îles d’Anvers et de Wiencke existe. L’incertitude sur la localisation « actuelle » des stations des îles d’Anvers et Wiencke et du cap Renard est certainement la plus importante de toutes les stations.

5. Îles Wauwermans (WA)

74La station des îles Wauwermans n’a pas été prise en compte car il s’agit d’un archipel d’îles très dispersées. La station se trouve certainement sur une des îles sud-orientales, mais, faute de détails suffisants sur la « carte » de Lecointe (1903b), nous n’avons pu déterminer la localisation de cette station sur les documents actuels.

IV. Résultats de la comparaison de coordonnées

75Le Tableau 2 montre les coordonnées calculées par Lecointe (nd et 1903a) et celles que nous avons déterminées par interprétation des ressources cartographiques actuelles en les comparant à la « carte » du détroit (Lecointe, 1903b). Les deux positions sont symbolisées sur la Figure 5.

Nom	Lecointe 1898		Auteurs de l’article *
	Longitude naturelle	Latitude naturelle	Longitude Géodésique WGS 84	Latitude Géodésique WGS84
Cap Neyt	61°47’15’’W	63°57’06’’S	61°49’32’’W	63°58’11’’S
Ile Auguste	61°35’03’’W	64°02’26’’S	61°37’52’’W	64°03’14’’S
Ile Harry	61°58’45’’W	64°07’19’’S	61°60’43’’W	64°07’27’’S
Récifs près de l’Ile Louise	62°22’W	64°31’S	62°23’34’’W	64°36’15’’S
Ile Anvers	62°56’W	64°31’38’’S	61°05’49’’W	64°38’10’’S
Ile Wiencke	63°29’01’’W	64°47’S	63°25’28’’W	64°47’25’’S
Terre de Danco Cap Renard	63°49’46’’W	65°01’26’’S	63°51’04’’W	65°03’33’’S
Une des Iles Moureaux	63°00’27’’W	65°04’24’’S	63°07’17’’W	65°05’26’’S
Iles Wauwermans	63°42’W	64°54’22’’S
Ile Cobalescou	61°36’00’’W	64°08’30’’S	61°39’07’’W	64°11’46’’S
Vu l’incertitude de ses coordonnées, la station “à bord” près du cap von Sterneck n’a pas été retenue
Toutes les observations du tableau ont été réalisées “sur la terre” sauf celles de l’Ile Cobalescou qui ont été faites “à bord”
63°57’06’’S	Calcul de Lecointe (nd) : Précision à 15 secondes d’arc
64°31’W	Calcul de Lecointe (nd) : Précision à la minute d’arc
* Ressources cartographiques utilisées par les auteurs de l’article :
BAS1	Carte du BAS imprimée au 1 : 250 000
BAS2	Base de données géographiques du BAS
GE	Google Earth
LIMA	Landsat Image Mosaic of Antarctica

Tableau 2. Coordonnées des stations principales calculées par Lecointe (nd et 1903a) et celles obtenues par un des auteurs de cet article (Y. Cornet) en utilisant les ressources cartographiques actuelles.

76On constate que les longitudes et latitudes proposées par Lecointe (nd et 1903a) sont biaisées (Figure 10). Une erreur systématique affecte presque toutes les coordonnées calculées par Lecointe (nd et 1903a) ; les stations sont trop à l’est et au nord par rapport à leurs coordonnées « actuelles ».

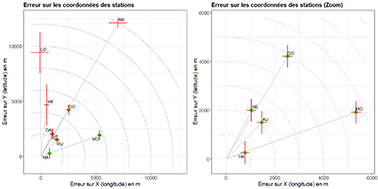
Figure 10. Erreurs, estimées à partir des positions « actuelles » (interprétation de Y. Cornet), sur les coordonnées calculées par Lecointe en 1898. Les étiquettes ont la même signification que sur la figure 5. Les barres d’imprécision en rouge correspondent aux imprécisions de ±15’’ ou ±1’ considérées par Lecointe (1903a). Les points verts correspondent aux stations dont la position actuelle a été interprétée avec une certitude satisfaisante.

Chronomètre	Erreur sur l’heure	Erreur sur la longitude à 64°S
	1 sec	203 m
Arrondi (Lecointe, nd) Sextant-Chronomètre- Méthode	Arrondi (lat. ou long.)	Erreur sur la longitude à 64°S	Erreur sur la latitude
	1’’	14 m	31 m
	15’’	203 m	463 m
	1’’	812 m	1853 m

Tableau 3. Imprécisions attendues sur les coordonnées calculées par Lecointe (1903a)

77La position « actuelle » interprétée de LO, AN, WI, DA et WA est trop peu fiable que pour discuter l’incertitude des coordonnées calculées par Lecointe. Dès lors, seules les 5 stations dont la position « actuelle » a été interprétée avec le plus de certitude peuvent être exploitées pour analyser l’incertitude des coordonnées calculées par Lecointe. Deux d’entre elles (AU et HA) présentent un faible biais relativement aux autres stations. Les deux autres (CO et MO) présentent un biais beaucoup plus important. La cinquième, NE montre un biais comparable à AU.

78Les coordonnées de HA ont été calculées à partir de 2 droites de hauteur en début de matinée. Cela explique le faible biais dont une part importante est probablement liée à l’incertitude sur la position « actuelle ».

79Les coordonnées de AU ont été estimées en combinant trois méthodes, une méridienne le 26 janvier ainsi qu’une droite de hauteur et l’angle horaire le 27 janvier à 6h45 du matin. Cette combinaison produit un biais assez faible dont la valeur est très marginalement influencée par la position « actuelle » fiable.

80À CO, une seule observation méridienne a été faite « à bord » et cela explique probablement un biais plus important et équivalent en latitude et longitude. Les incertitudes sur la hauteur vraie (horizon de la mer, correction de la réfraction même si l’angle vertical solaire est proche de 45°...), le moment de la culmination en raison de la trajectoire peu courbée du soleil et l’heure des chronomètres se combinent probablement ici pour produire un tel biais supérieur à l’incertitude sur les coordonnées « actuelles ».

81Les coordonnées de MO calculées par la méthode la moins précise de l’angle horaire à 9h du matin sont affectées d’un biais très important en longitude. L’heure matinale des observations en est certainement la principale cause (azimut des observations proche de 90°) en association avec la faible hauteur du soleil et la correction approximative de la réfraction. L’incertitude sur l’heure affecte peut-être aussi le calcul de l’angle horaire, mais il est très peu probable que celle-ci explique de façon significative le biais de ~2 500 m sur la longitude, une erreur d’une seconde de temps à la latitude de 64° provoquant une erreur de ~203 m d’arc de longitude.

82La direction des vecteurs-erreur pour les stations HA, AU et MO montre un azimut supérieur à 45°. Les observations y ont été faites assez tôt le matin avec un soleil bas au-dessus de l’horizon (Tableau 1). Même si la correction de réfraction calculée par Lecointe correspond à celle que nous avons calculée (Tableau 1), elle reste approximative et se répercute donc sur le biais en longitude lorsque les observations sont faites à ce moment de la journée.

83À NE, selon l’endroit où les observations auraient été faites, dans la baie ou sur un des deux caps qui la délimitent, la composante latitudinale restera importante et la composante longitudinale pourrait être légèrement réduite ou augmentée (de l’ordre de 400 m) à la suite d’une mesure du temps imparfaite. Il s’agit de la seule station où une droite de hauteur a été observée l’après-midi. Malgré cela, le biais est orienté vers le nord-est peut-être en raison de l’erreur sur la position approchée. Mais, dans ce cas, il faut peut-être aussi invoquer l’effet de la connaissance imprécise du temps !

V. Discussion des causes possibles du biais constaté

A. Déviation de la verticale

84Le premier élément qui peut expliquer le biais de coordonnées constaté est la méthode simplificatrice que nous avons adoptée pour mesurer, par une simple différence, l’écart entre les coordonnées astronomiques calculées par Lecointe en 1898 et les coordonnées géodésiques modernes exprimées dans le datum WGS84.

85à ce sujet, Malys et al. (2015) nous rappellent qu’en 1884, la Conférence internationale de Washington a recommandé que le méridien « origine » soit employé comme zéro commun de longitude et norme de calcul du temps dans le monde entier. Il s’agit du méridien correspondant au Cercle de Transit de Airy installé à l’Observatoire de Greenwich.

86Aujourd’hui, les récepteurs de navigation par satellite indiquent la longitude géodésique zéro environ 102 m plus à l’est. Malys et al. (2015) expliquent ce décalage à Greenwich par la différence entre les coordonnées astronomiques et géodésiques qui correspond à la composante est-ouest de la déviation de la verticale et par la condition imposée de continuité du temps astronomique. Ce décalage est lié à l’exigence des récepteurs de navigation par satellite dont les coordonnées sont fournies dans un système géocentrique. Le méridien de référence pour la navigation satellitaire doit donc passer par le centre de masse de la Terre, ce qui n’était pas le cas du méridien « origine » imposé en 1884. Les méridiens correspondant aux deux systèmes sont parallèles car cela garantit que la mesure du Temps Universel n’a pas changé.

87Selon Malys et al. (2015), il ne s’est donc pas produit de rotation systématique des longitudes globales entre l’ancien système astronomique et le système géodésique actuel. Ces chercheurs ont démontré que la différence entre des coordonnées GNSS précises et des coordonnées déterminées astronomiquement correspond partout sur Terre à la déviation de la verticale locale et qu’il est possible d’estimer les deux composantes de cette déviation en mesurant la pente et son orientation du modèle de géoïde EGM2008. Ces deux composantes sont notées ηgrav ~= η et ξgrav ~= ξ, respectivement selon la longitude et la latitude. La différence entre longitude astronomique (Λ ~= Λgrav) et longitude géodésique (λ) vaut dès lors ηgrav sec(φ). La différence entre latitude astronomique (Φ ~= Φgrav) et latitude géodésique (φ) vaut dès lors ξgrav.

88Nous avons implémenté cette méthode pour estimer ces composantes aux stations mentionnées par Malys et al. La comparaison de nos résultats à ceux de ces auteurs montre la fiabilité de notre calcul (Tableau 4).

ID	φ	λ	ηgrav sec(φ) en arc-sec (nos calculs)	ηgrav sec(φ) en arc-sec (Malys et al.)	Différence
G	51,47781	-0,00147	5,6	4,9	0,7
BLI	44,80014	20,51303	1,9	1,5	0,4
BOI	52,27519	17,07492	7,5	7,4	0,1
BG	52,47553	21,03475	8,9	8,9	0,0
BS	47,24806	5,98925	-6,9	-6,4	-0,5
CT	-33,93481	18,47750	-0,7	-0,4	-0,3
G	50,87256	0,33736	2,0	1,5	0,5
GRA	43,75202	6,92364	11,2	12,2	-1,0
MA	55,70133	37,54183	9,1	9,2	-0,1
MS	-35,32094	149,00641	-4,3	-4,5	0,2
NK	46,97206	31,97367	4,7	4,5	0,2
O	45,39325	-75,71469	-5,0	-5,1	0,1
OJP	49,91400	14,78367	7,6	7,1	0,5
OS	45,40019	-75,91897	-5,0	-4,2	-0,8
PA	48,83572	2,33708	2,2	2,3	-0,1
PTA	52,38014	13,06497	6,4	6,4	0,0
PTP	52,40503	13,10311	6,7	6,7	0,0
PUG	59,77006	30,32619	3,8	4	-0,2
PYD	49,91403	14,78669	7,6	8,1	-0,5
RCA	25,61411	-80,38417	7,5	7,8	-0,3
SFA	36,46578	-62,05000	0,0	-0,3	0,3
SJ	-31,50944	-68,62378	14,3	14,4	-0,1
SP	-23,65242	-46,62239	0,1	0,3	-0,2
TFA	-53,78569	-67,75106	0,6	0,6	0,0
UA	50,79722	4,35878	-4,2	-4,7	0,5
W	38,92142	-77,06706	4,4	4,4	0,0

Tableau 4. Valeurs de ηgrav sec(φ) calculées par Malys et al. (2015) et celles que nous avons calculées. La différence réside très probablement dans le fait que nous avons estimé la valeur au plus proche voisin de la grille EGM2008 et que Malys et al. ont certainement utilisé une technique d’interpolation plus fine.

89Nous l’avons donc appliquée aux stations levées par Lecointe (Tableau 5). Pour les seules stations dont la position « actuelle » a été interprétée avec le plus de certitude (NE, AU, HA, MO et CO), il en ressort que la déviation de la verticale y produit des écarts attendus en longitude de signe opposé à celui que nous avons observé et d’un ordre de grandeur en valeur absolue très inférieur à celui que nous avons observé. Pour la latitude, les écarts attendus sont du même signe que celui observé sauf pour MO et d’un ordre de grandeur aussi très inférieur.

	Φ	Λ	(Λgrav ‒ λ) en arc-sec	(Φgrav ‒ φ) en arc-sec	λ attendu	φ attendu	dx attendu en m	dy attendu en m	dx observé en m	dy observé en m
NE	-63,96961	-61,80891	-6,9	2,9	-61,80700	-63,97041	-96,0	88,8	1044,7	1995,7
AU	-64,05394	-61,61445	-12,1	2,1	-61,61108	-64,05453	-169,9	65,5	1473,4	1488,3
HA	-64,12423	-61,99527	-8,1	1,8	-61,99302	-64,12473	-113,2	56,1	781,3	254,2
LO	-64,60127	-62,36492	-7,9	-1,4	-62,36271	-64,60088	-111,2	-43,7	-83,4	9408,0
AN	-64,63611	-63,08019	-12,4	-0,4	-63,07674	-64,63600	-173,9	-12,0	6995,5	12108,1
WI	-64,82529	-63,49459	-14,2	-2,3	-63,49063	-64,82465	-199,3	-71,4	519,2	4665,6
DA	-65,04255	-63,85118	-18,0	-0,3	-63,84617	-65,04247	-252,4	-8,9	1019,7	2075,5
MO	-65,09054	-63,12147	-10,9	-1,0	-63,11843	-65,09027	-152,9	-30,2	5337,8	1913,8
CO	-64,17947	-61,65208	-10,1	0,8	-61,64928	-64,17969	-141,3	23,9	2522,4	4204,1

Tableau 5. Valeurs des différences (Λgrav ‒ λ) et (Φgrav ‒ φ) attendues en fonction de la déviation de la verticale aux stations levées par Lecointe en 1898.

90On peut dès lors difficilement invoquer cette raison à elle seule pour expliquer le biais de coordonnées observé.

B. Le choix du rayon terrestre moyen

91Dans notre méthode de comparaison des coordonnées, un deuxième facteur influence l’importance des écarts entre coordonnées astronomiques et géodésiques actuelles. Il s’agit du rayon terrestre moyen adopté. Dans nos calculs, nous avons utilisé le rayon de la sphère authalique de Clarke, soit 6371228 m. L’utilisation d’autres valeurs de rayon moyen résultant de l’application de diverses méthodes de calcul proposées dans la littérature produit des variations qui sont de l’ordre d’une dizaine de mètres soit un ordre de grandeur bien inférieur aux écarts observés.

92La valeur de ce rayon moyen est un simple facteur d’échelle pour passer d’unités de mesure angulaire à des unités métriques qui ne peuvent en rien expliquer le biais constaté. Il faut donc invoquer d’autres causes pour expliquer ce dernier.

C. Réfraction, heure d’observation et propagation de l’erreur sur la position approchée

93Il est bien connu que la sous-estimation de la correction de réfraction est une des sources d’erreur systématique sur l’estimation de coordonnées par observations astronomiques (Remy, 1909 ; Loodts, 1966). Pour y remédier, il est recommandé de réaliser des observations selon des azimuts bien répartis et opposés comme l’illustre la Figure 11.

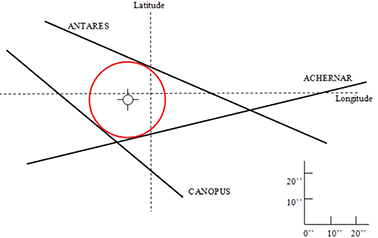
Figure 11. Calcul des coordonnées du Pilier Astronomique de la Base Roi Baudouin réalisé par J.-J. Dewael et M. Foccroulle en observant 3 étoiles (cas plus favorable que la lune ou le soleil, car l’étoile est assimilable à un point) le 6 juillet 1965 avec des instruments performants, en mesurant le temps au signal horaire WWD et en construisant graphiquement les 3 droites de hauteur leur correspondant. Le centre du cercle inscrit dans le triangle constitué par ces droites est la position la plus probable. On remarque que, malgré la plus grande qualité des observations, chaque droite est quand-même déplacée vers l’astre observé en raison d’une source d’erreur systématique (réfraction), mais leur combinaison avec des azimuts bien distribués permet de les compenser (source : J.-J. Derwael, documentation personnelle de sa mission de géodésien en Antarctique).

94Des observations bien réparties en azimut n’ont malheureusement pas été possibles pendant l’exploration du détroit de Gerlache en 1898. Ainsi, la sous-estimation de la réfraction produit une hauteur Hv probablement systématiquement surestimée. Par ailleurs, l’estimation de la hauteur attendue He en calculant la distance zénithale du soleil sur base de la position approchée de la station, de la position du point subsolaire donné par les éphémérides, de la mesure du temps et de l’équation du temps permet par la méthode des droites de hauteur de déterminer l’intercept. Ce dernier vaut Hv-He et est la correction à appliquer à la position approchée le long de l’orthodromie joignant celle-ci au point subsolaire. Si, en première approximation, on considère que le point subsolaire est connu sans incertitude, on peut envisager 3 configurations azimutales de l’observation du soleil selon l’heure de l’observation.

1. Observation vers le soleil à l’est

95Si l’observation est réalisée selon un azimut de 90°, le matin, l’intercept sera surestimé et la position sera donc corrigée vers l’est avec excès. L’erreur en latitude sur la position approchée sera quasiment totalement propagée sur la position corrigée, car la distance entre ces deux points est beaucoup plus petite que la distance par rapport au point subsolaire. Étant donné que la position approchée découle toujours d’observations du soleil avec surestimation de Hv, la position corrigée se trouvera toujours trop au nord et, donc, au nord-est si on combine les deux sources d’erreur.

2. Observation vers le soleil au nord

96Si l’observation est réalisée selon un azimut de 0°, à midi (observation méridienne – droite de hauteur ouest-est), la surestimation de Hv produira une position corrigée trop au nord (30 seconde d’arc de méridien valant ~930 m) et l’erreur en longitude héritée de la position approchée produira une position corrigée trop à l’est et, donc trop au nord-est en réalisant la même combinaison que ci-dessus.

3. Observation selon un azimut intermédiaire entre 0° et 90°

97Les observations intermédiaires, comme la majorité de celles effectuées par Lecointe à l’exception de la station NE, combineront les deux configurations précédentes pour produire une position corrigée trop au nord-est, telle que nous l’avons constatée (Figure 10).

D. Erreur sur la mesure du temps

98L’erreur sur la mesure du temps négligée en première approximation peut être de trois types : une dérive progressive, des fluctuations de part et d’autre de cette dérive et des sauts aléatoires.

99La dérive progressive se manifeste quand les chronomètres ne peuvent être réglés. Une mesure du temps qui retarde produira un biais vers l’est qui s’accroît avec le temps. Selon Lecointe (1901a et b), les réglages des 30/12/1897 et 14/03/1898 encadrent la période d’exploration du détroit de Gerlache. Les corrections apportées a posteriori sur la marche des chronomètres devrait avoir réduit en grande partie l’effet de cette dérive. Ainsi, l’importance du biais longitudinal dû à cette dérive ne peut être aussi important que celui constaté. En effet, rappelons que selon Yvon-Villarceau (1875, in Boistel, 2006), en soixante-huit jours de mer, cinq chronomètres de marine n’ont pas dévié de plus de l’équivalent de six secondes, soit ~85 m d’arc en longitude à la latitude de 64°S du détroit.

100La Figure 5 montre une variation spatiale du biais. Il est relativement plus petit au nord-est du détroit à NE, HA, AU et CO (mais il s’agit des stations dont les positions « actuelles » sont aussi les plus certaines) et atteint un maximum au milieu du détroit, à AN et LO visitées le 30 janvier et le 8 février (mais il s’agit de deux stations dont les coordonnées « actuelles » sont très incertaines). Ensuite, il diminue (WI et DA visitées les 9 et 12 février et dont la position actuelle est aussi incertaine). Cependant, MO (dont la position « actuelle » est très certaine) visitée le 11 février montre un biais plus important que WI et DA, surtout en longitude.

101La comparaison des premières stations visitées dont la position « actuelle » est certaine (NE, HA, AU et CO) à la station MO visitée le 11 février montre peut-être une tendance temporelle du biais, éventuellement liée à une dérive des chronomètres puisqu’elle concerne plus spécifiquement la longitude. Si elle existe, celle-ci reste faible par rapport aux autres sources d’erreur, telles que la mesure des angles, la correction de la réfraction, la méthode de calcul (droites de hauteur et l’heure de leurs observations, angle horaire, méridienne ou circum-méridienne) et l’incertitude de l’interprétation de la position « actuelle » prise comme référence.

102La fluctuation de part et d’autre de cette dérive est due en grande partie à l’influence de la température et enfin les sauts aléatoires sont généralement évités par l’utilisation de plusieurs chronomètres. La marche diurne des chronomètres (Figure 7) et la méticulosité de la mesure le temps telle que rapportée par Lecointe (1901a et b) attestent que l’on peut difficilement retenir l’hypothèse d’un important biais en longitude causé par cette mesure, même si Westerlinck (communication au colloque organisé par Decleir et de Broyer (1998)) considère que l’erreur de chronomètre influençant l’incertitude sur la longitude pourrait atteindre plusieurs miles nautiques (1 mile nautique = 1852 m).

103Néanmoins, le cas de la station NE où les mesures ont été faites l’après-midi et qui est aussi positionnée trop à l’est montre probablement qu’il ne faut pas complètement négliger cette source d’erreur sur la mesure du temps qui, à NE, se combine peut-être à l’erreur sur la longitude de la position approchée !

E. Erreur sur la détermination de l’azimut géographique

104Il semble que seules les coordonnées de 3 stations (AU, AN, DA) ont été estimées en exploitant des observations méridiennes ou circum-méridiennes combinées à une autre méthode (angle horaire) pour deux des cas (AU et DA). Pour les autres stations, l’azimut géographique du soleil a donc très probablement été mesuré en utilisant le compas donnant un azimut magnétique instrumental qui doit avoir été corrigé de la déclinaison magnétique estimée par Danco le 13 février, mais rien n’est dit à ce sujet dans les documents que nous avons consultés. Une surestimation de cette déclinaison peut avoir provoqué une légère surestimation de l’azimut géographique du soleil observé dans les méthodes des droites de hauteur et de l’angle horaire contribuant peut-être en partie aux coordonnées biaisées constatées.

F. Le cas du calcul des coordonnées de l’Ile Harry

105Le calcul des coordonnées de l’Ile Harry exploite deux droites de hauteur. Des corrections en latitude et en longitude sont appliquées au point déterminatif Z1. Pour le calcul de la latitude de Z, on a :

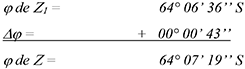
106Pour le calcul de la longitude, la longitude de Z1 devrait 61° 59’ 00’’ W pour obtenir la longitude de Z publiée par Lecointe (Tableau 1) :

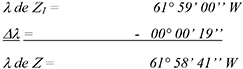
107Or, la longitude de Z1 trouvée dans Lecointe (nd et 1903a) n’est pas 61° 59’ 00’’ W mais semble plutôt être 61° 58’ 00’’ W. Cela produirait un biais en longitude plus important ! Nous n’avons pas trouvé l’origine de cette incohérence apparente plutôt favorable au résultat de Lecointe.

Conclusion

108Notre analyse démontre clairement qu’il a été possible de comparer les coordonnées calculées par Lecointe en 1898 aux coordonnées géodésiques actuelles pour les stations dont nous avons pu interpréter la position sur les documents cartographiques actuels avec le plus de certitude. Le biais constaté vers le quadrant nord-est ne semble pas lié à la déviation de la verticale. Il semble aussi que l’erreur causée par la mesure du temps ne peut être évoquée pour expliquer ce biais. La seule raison que nous pouvons retenir est le fait que Lecointe a réalisé quasiment toutes ses observations en matinée et qu’il n’a donc pas été en mesure d’éliminer les erreurs produites notamment par la réfraction.

109Lecointe (1904) conclut à la fin de l’exploration du détroit : « L’itinéraire suivi par la Belgica indique avec quel soin le terrain a été fouillé. Le parcours du détroit a duré vingt jours, pendant lesquels nous avons noté, avec une scrupuleuse attention, tous les renseignements qui pourraient intéresser, dans ces parages, les futurs navigateurs ». En suivant l’itinéraire du trois-mâts et les 20 débarquements effectués, on se rend compte avec quel soin les Belges ont exploré les terres qu’ils découvraient (Brent, 1997).

110La comparaison des Figures 1, 2 et 5 atteste de l’apport cartographique exceptionnel de l’exploration. Considérant les instruments de mesure dont disposait l’expédition et la durée limitée du séjour dans le détroit pendant l’été austral sans voir d’autres astres que le soleil et souvent par mauvais temps, la réalisation d’une carte d’une telle qualité est remarquable. Pour l’époque, cette carte est le résultat d’un travail minutieux et d’un grand professionnalisme.

111Lecointe (1903a) lui-même remarque que durant le séjour dans le détroit de Gerlache plusieurs éléments ont entravé les observations astronomiques. Il n’y avait pas d’étoiles visibles (24 heures de clarté); la lune n’était pas visible non plus et la faible hauteur du soleil au-dessus de l’horizon a certainement contribué à augmenter les erreurs de réfraction.

112La rigueur de ce travail est d’ailleurs mise en exergue par Westerlinck (communication au colloque organisé par Decleir et De Broyer, 1998) qui écrit à ce sujet : ”It is a fact that the Belgica has achieved a remarkable expedition. Indeed, comparing the Belgian chart with the Admiralty chart and the German chart “Original Karte des Dirck Gerritz Archipels” of that time, one may say, in particular to Graham Land, that the Belgian expedition has performed an extraordinary achievement.”

113La publication de la carte ”Sketch of Danco Land the Belgica Strait and Palmer Archipelago” dans le Geographical Journal – Royal Geographical Society (1901) peut d’ailleurs être considérée comme une reconnaissance de la qualité du travail effectué.

Remerciements

114Les auteurs sont spécialement reconnaissants à Guido Kips (KUL) et Jean-Paul Donnay (ULiège) qui ont eu la gentillesse de relire consciencieusement leur manuscrit et proposer des améliorations très significatives. Ils remercient également Claude De Broyer (Institut Royal Belge des Sciences Naturelles), Jozef Verlinden (biographe d’Adrien de Gerlache) et Hugo Decleir (VUB).

Bibliographie

115Arctowski H., 1901. The Antarctic voyage of the “Belgica” during the years 1997, 1998 and 1999. The Geographical Journal, Vol. 18, No. 4, 353-390

116Boistel G., 2006. De quelle précision a-t-on réellement besoin en mer ? Quelques aspects de la diffusion des méthodes de détermination astronomique et chronométrique des longitudes en mer en France, de Lacaille à Mouchez (1750-1880). Histoire & mesure, 2006/2 (Vol. XXI), 121-156. https://www.cairn.info/revue-histoire-et-mesure-2006-2-page-121.htm

117Brent M., 1997. L’Antarctique et la Belgique – Cent ans d’Histoire, de recherches et de mystères. Editions Labor Bruxelles.

118Decleir H. et de Broyer C., 1998. The Belgica Expedition Centennial Perspectives on Antarctic Science and History. Proceedings of the Belgica Centennial Symposium, 14-16 May 1998, Brussels.

119Decleir H. [ed.], 1998. Roald Amundsen’s Belgica Diary. The first scientific expedition to the Antarctic (Titre original: Amundsens dagbog, unpublished), Hadewijcn Publishing Company.

120de Gerlache de Gomery A., 1901. Expédition Antarctique Belge. Résultats du Voyage du S. Y. Belgica en 1897 - 1898 - 1899 sous le commandement de A. de Gerlache de Gomery. Rapports scientifiques publiés aux frais du gouvernement Belge, sous la direction de la commission de la Belgica.

121de Gerlache de Gomery A., 1902. Voyage de la Belgica – Quinze mois dans l’Antarctique. G. Lebègue et Cie – Bruxelles.

122Dethinne T., Glaude Q., Amory Ch., Kittel Chr., Fettweis X., 2022. Comparison between surface melt estimation from Sentinel-1 synthetic aperture radar and a regional climate model. Case study over the Roi Baudouin ice shelf, East Antarctica. Bulletin de la Société Géographique de Liège, N° 78, pp. 113-122, https://popups.uliege.be/0770-7576/index.php?id=6644.

123Dufour J.Ph., 2001. Introduction à la géodésie. Coll. ENSG-IGN, Hermes, 334 p.

124Duhamel M., 1949. Déterminations astronomiques en campagne. Institut Géographique National - Ecole Nationale des Sciences Géographiques, Paris.

125Hutchinson D.L., 1908. Wireless times signals from St John Observatory of the Canadian Meteorological Service. Proceedings and Transactions of the Royal Society of Canada, Ser. 3, Vol. 2, pp. 153-154.

126Jonkers A.R.T., Jackson A., Murray A., 2003. Four centuries of geomagnetic data from historical records. Reviews of Geophysics, Volume 41, Issue 2, https://doi.org/10.1029/2002RG000115.

127Lahaye B., 2010, Spatiocartographie à petite échelle de la station belge Princess Elisabeth en Antarctique. Mémoire de Master en Sc. Géographiques, inédit, Uliège.

128Lecointe G., nd. « Voyage de la Belgica - Positions observées du 28 août 1897 au 5 mars 1898 ». Notes manuscrites de G. Lecointe contenant les fiches de calcul de positions.

129Lecointe G., 1901a. Astronomie – Etude des chronomètres – Première partie, Méthode et Conclusions - Expédition Antarctique Belge Résultats du Voyage de la Belgica en 1897–99 Rapports Scientifiques, Imprimerie J.-E. Buschmann, Anvers.

130Lecointe G., 1901b. Astronomie – Etude des chronomètres – Deuxième partie, Journaux et Calculs Expédition Antarctique Belge Résultats du Voyage de la Belgica en 1897-1898-1899 . Rapports Scientifiques, Imprimerie J.-E. Buschmann, Anvers.

131Lecointe G., 1903a. Travaux hydrographiques et instructions nautiques - Cartes - Expédition Antarctique Belge Résultats du Voyage de la Belgica en 1897-1898-1899. Premier Fascicule. Rapports Scientifiques, Imprimerie J.-E. Buschmann, Anvers.

132Lecointe G., 1903b. Travaux hydrographiques et instructions nautiques - Expédition Antarctique Belge, Résultats du Voyage de la Belgica en 1897-1898-1899. Cartes. Rapports Scientifiques, Imprimerie J.-E. Buschmann, Anvers. https://www.vliz.be/imisdocs/publications/ocrd/155443.pdf

133Lecointe G., 1904. Au Pays des Manchots – Récit du voyage de la Belgica. Société Belge de Librairie. Oscar Schepens & Cie, Editeurs, Bruxelles.

134Loodts J., 1966. Géodésie et topographie dans l’Antarctique. Ciel et Terre, Vol. 82, p. 85. https://adsabs.harvard.edu/full/1966C%26T....82...85L.

135Malys S., Seago J.H.,· Pavlis N.K., Seidelmann P.K. & Kaplan G.H., 2015. Why the Greenwich meridian moved? Journal of Geodesy, 89, pp. 1263–1272. https://www.doi.org/10.1007/s00190-015-0844-y.

136Remy E, 1909. La détermination de la position géographique dans la navigation ancienne et dans la navigation moderne, Ciel et Terre, Vol. 30, p.8. https://articles.adsabs.harvard.edu//full/1909C%26T....30....8R/0000008.000.html.

137The IMBIE team, 2018. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature, volume 558, pp. 219–222, https://www.nature.com/articles/s41586-018-0179-y.

138Verlinden J., 2008. Discovery and Exploration of Gerlache Strait. Publié par Daniel Desmet Asteria Expeditions, Brugge.

139Williams R. S. Jr., Ferrigno J. G., Kent T. M., Schoonmaker J. W. Jr., 1982. Landsat Images and Mosaics of Antarctica for Mapping and Glaciological Studies. Annals of Glaciology, Vol. 3, pp. 321-326, https://doi.org/10.3189/S0260305500003001.

140Zhang N. & Talalay P.G., 2021. Antarctic oil and mineral resources: a subject off limits or future reality? Earth’s Future, https://doi.org/10.1002/essoar.10505822.1

Sites Web consultés (dernière consultation 2/6/2022) :

141Web 1. https://pubs.usgs.gov/fs/2007/3116/

142Web 2. https://www.bas.ac.uk/data/our-data/maps/topographic-maps/northern-antarctic-peninsula/

143Web 3. https://data.bas.ac.uk/collections/e74543c0-4c4e-4b41-aa33-5bb2f67df389/

144Web 4. https://www.usgs.gov/programs/geomagnetism/introduction-geomagnetism

145Web 5. https://www.usgs.gov/media/images/declination

Cartes

146Carte de l’Amirauté Anglaise (Lecointe, 1903b).

147Carte de L. Friederichsen (Lecointe, 1903b).

148Carte imprimée de la Péninsule Antarctique Septentrionale (Northern Antarctic Peninsula) (BAS(UKAHT)) produite par le British Antactic Survey. Editions de 2008 et 2017.

149Croquis provisoire du détroit de la Belgica - Dressé par le Lieutenant de Vaisseau Lecointe, Commandant en second de l’Expédition (Lecointe, 1903b).

150Croquis provisoire du détroit de Gerlache - Levé par MM. de Gerlache et Lecointe et dressé par M. Lecointe (Lecointe, 1903b).

151Carte V. Expédition antarctique belge. Détroit de Gerlache. Levé rapide exécuté par MM. de Gerlache et Lecointe et dressé par Lecointe Commandant en second de l’Expédition (Lecointe, 1903b).

152Sketch of Danco Land, the Belgica Strait and Palmer Archipelago Surveyed by Capt G. Lecointe – 1898. Publiée dans le Geographical Journal – Royal Geographical Society (1901).

153Nous mettons à la disposition du lecteur quelques documents complémentaires (Fichiers - DoX @ CHU-ULiège (uliege.be) “https://dox.uliege.be/index.php/s/ByHpnJ33VvEotsh”). Il s’agit :

154- d’un fichier Excel avec les mesures réalisées pour valider l’hypothèse de la projection équi-rectangulaire avec une latitude de référence de l’ordre de 64°S utilisée par Lecointe.

155- d’un script R de calcul des deux composantes de la déviation de la verticale

Pour citer cet article