Jean-Paul KASPRZYK & Nadia Poncelet

Complémentarité des modèles vecteur et raster dans les cubes de données spatiaux destinés à l'analyse de risque. Application pour les services d'urgence bruxellois

Résumé

Un outil d’analyse décisionnelle (BI) a été développé dans le but de faciliter l’analyse des risques territoriaux pour les services de secours bruxellois. Notre hypothèse est qu’un système de processus analytiques spatiaux en ligne (SOLAP) hybride, alliant des cubes de données de types raster et vecteur, peut améliorer l’analyse de la répartition spatiale des risques récurrents. Il permet la comparaison entre des cartes de densité de risque construites par estimateurs à noyaux de densité (KDE) et des cartes de densité de risque basées sur des nombres absolus d’interventions par entité géographique vectorielle. Nous exploitons ici un métamodèle unique pour l’instanciation des modèles de cubes, la gestion des opérations SOLAP (filtres, forages) et la navigation dans une constellation hybride raster/vecteur. Une décomposition des cubes raster en cuboïdes est proposée afin de garantir des opérations de forages fluides pour l’utilisateur. Une autre originalité de cet outil SOLAP est la possibilité d’y intégrer un niveau de dimension géographique qui évolue en fonction du positionnement des postes de secours simulé par l’utilisateur, tout en tenant compte des contraintes de vitesse du réseau routier bruxellois.

Abstract

A Business Intelligence (BI) tool has been developed in order to facilitate the analysis of territorial risks for the Brussels emergency services. Our hypothesis is that a hybrid SOLAP combining raster and vector data cubes can improve the analysis of the spatial distribution of recurrent risks, by allowing the comparison between risk density maps built using Kernel Density Estimation (KDE) and risk density maps based on absolute numbers of interventions per geographic vector entity. We use here a unique metamodel for the instantiation of the cube models, the management of SOLAP operations (filters, drillings) and the navigation in a hybrid raster/vector constellation. We propose a decomposition of the raster cubes into cuboids in order to guarantee fast drilling operations for the user. Another originality of this SOLAP tool is the possibility to integrate a geographic dimension level that evolves according to the positioning of the rescue stations simulated by the user while taking into account the speed constraints of the Brussels road network.

Table des matières

Introduction

1Depuis l’explosion du big data, l’aide à la décision s’appuie sur l’analyse de géodonnées toujours plus nombreuses et diversifiées. Afin d’extraire des informations utiles hors de ces très grands jeux de données, les outils d’analyse décisionnelle (Business Intelligence, BI) sont devenus indispensables pour l’analyse de cubes de données dans une grande variété de domaines : géomarketing, aménagement du territoire, observation de la Terre, analyse criminelle, etc.

2Cette recherche s’intéresse particulièrement à l’exploitation des outils BI en analyse du risque destinée aux services d’urgence (pompiers et aides médicales urgentes). L’objectif de ce type d’analyse est d’optimiser la répartition spatio-temporelle des ressources humaines et matérielles sur un territoire, afin d’arriver le plus rapidement possible sur un lieu d’incident, tout en évitant la saturation des postes de secours concernés. Il s’agit d’un problème complexe nécessitant notamment une analyse multidimensionnelle des interventions passées, croisée avec les données de circulation routière.

3En 2017, un projet visant à se munir d’un outil d’analyse de risque a été réalisé pour le SIAMU (Service d’Incendie et d’Aide Médicale Urgente) de la Région de Bruxelles-Capitale (Kasprzyk et Donnay, 2017). Celui-ci visait le développement d’un outil BI de type Spatial OnLine Analytical Processing (SOLAP) permettant notamment d’analyser un cube de données spatiales sur les interventions passées, afin de le comparer à l’accessibilité des postes de secours via une interface cartographique. Cet outil, baptisé OSCAR 1.0 (Outil SIG pour la Cartographie et l’Analyse du Risque), exploitait des cubes de données raster permettant une visualisation spatialement continue des couches d’accessibilité et de densité d’interventions calculées par estimateurs à noyaux de densité (Kernel Density Estimation, KDE – Figure 1). En effet, la technique KDE permet de transformer de très grands ensembles de points (lieux d’interventions) en champs continus particulièrement adaptés à la visualisation cartographique (Chainey, 2013).

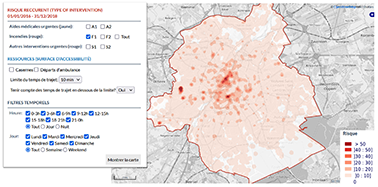
Figure 1. Carte KDE construite avec l'outil OSCAR 1.0

4L’avantage des cartes KDE est leur faculté d’agréger les données à travers des points chauds (hotspots) indépendants de toute frontière artificielle. En revanche, les valeurs de pixels associées au KDE sont parfois difficiles à interpréter et les services d’urgence bruxellois souhaitaient enrichir l’analyse SOLAP avec des nombres absolus d’interventions, afin de mieux évaluer la réponse au risque en termes d’hommes et d’équipements disponibles. L’objectif de cette nouvelle étude est donc la conception d’une nouvelle version de l’outil SOLAP (OSCAR 2.0) intégrant ces valeurs absolues tout en conservant les cartes de hotspots KDE dans l’analyse.

5La suite de cet article est structurée comme suit. En section I, nous dressons un état de l’art portant sur l’analyse de risque (A), l’informatique décisionnelle et l’OLAP (B), le SOLAP (C) et les métamodèles SOLAP (D). En section II, nous formulons notre hypothèse afin d’atteindre l’objectif de recherche. En section III, nous présentons le cas d’étude spécifique au SIAMU. En section IV, nous décrivons la méthodologie basée sur un métamodèle (A) instanciant une constellation de cubes de données (B), elle-même caractérisée par des secteurs d’interventions associés aux différents postes du SIAMU (C). En section V, nous présentons un cas d’utilisation de l’outil OSCAR 2.0. Finalement, la section VI conclut cet article.

I. État de l’art

A. Analyse de risque

6En Belgique, une loi de 2007 relative à la sécurité civile (Service Public Fédéral Intérieur, 2007) spécifie que les zones de secours doivent se munir d’une analyse des risques présents sur leur territoire et un arrêté royal de 2013 (Service Public Fédéral Intérieur, 2013) en fixe le contenu et les conditions minimales.

7Les risques y sont définis en deux catégories distinctes : d’une part, les risques récurrents, qui correspondent aux interventions du quotidien et qui peuvent être estimés sur une base statistique car ils sont représentés par un nombre suffisant d’observations dans le passé et, d’autre part, les risques ponctuels dont l’occurrence ne peut pas être estimée au moyen de statistiques mais qui correspondent à des lieux qui nécessiteraient des moyens importants en cas d’incident grave et, de ce fait, doivent être pris en compte dans la planification d’urgence (Chevalier et al., 2012).

8Les outils des systèmes d’information géographique (SIG) sont d’une grande aide pour confronter la répartition spatiale de ces risques avec l’accessibilité des postes de secours (p. ex. cartes isochrones montrant la zone couverte depuis une caserne endéans un certain laps de temps). Le présent article s’intéresse particulièrement à l’analyse cartographique du risque récurrent, bien que l’analyse du risque ponctuel et celle de l’accessibilité soient également intégrées dans OSCAR. Les cartes d’accessibilité nécessitent l’application d’un algorithme de calcul du plus court chemin. Dans le cas d’OSCAR, c’est l’algorithme de Dijkstra qui est appliqué sur les données routières d’OpenStreetMap (OSM) (Kazprzyk et Donnay, 2017 ; OSM, 2021). OSCAR est ainsi en mesure de proposer des cartes d’accessibilité depuis l’ensemble des postes de secours, soit dans la situation réelle, soit dans une situation simulée où la position des postes est définie par l’utilisateur.

9Des cartes d’accessibilité découle la notion de secteur d’intervention (voir section IV-C). Le secteur d’intervention d’un poste représente la zone dans laquelle ce poste sera théoriquement le premier à arriver sur place. Il peut être intéressant d’analyser localement le risque récurrent à l’échelle de ces secteurs afin d’évaluer dans quelle mesure les moyens (ressources en personnel et en matériel) y sont en adéquation avec les risques territoriaux.

B. Informatique décisionnelle et OLAP

10L’informatique décisionnelle (BI) désigne un ensemble d’outils adaptés à l’exploration et l’analyse de grands jeux de données (Negash et Gray, 2008). Une infrastructure BI typique comprend de multiples sources de données qui sont intégrées à un entrepôt de données par des procédures Extract, Transform, Load (ETL) (Badard et al., 2009). Les ETL automatisent les transformations de données vers une structure multidimensionnelle qui est le paradigme utilisé pour l’exploration et l’analyse des données.

11Un entrepôt de données archive des données multidimensionnelles selon une approche qualifiée de OLAP (Online Analytical Processing) (Kimball et Ross, 2013). Contrairement aux systèmes transactionnels, l’OLAP implique des procédures d’agrégations complexes mais exécutées rapidement afin de synthétiser les données dans des tableaux ou des graphiques. Ces agrégations exploitent différents niveaux de granularité (agrégation) d’une même donnée selon des dimensions hiérarchisées en niveaux (p. ex. données temporelles par année, par mois, par semaine, etc.).

12L’exploration et l’analyse d’un entrepôt de données sont effectuées par des outils OLAP. Ceux-ci interprètent la structure multidimensionnelle des données afin de les représenter efficacement dans des interfaces conviviales. Les données sont ainsi modélisées sous la forme de cubes de données caractérisés par des axes de dimension (p. ex. temps, lieu, type de produit, etc.) indexant des variables, appelées mesures, qui peuvent être représentées dans des tableaux ou graphiques dynamiques. Chaque mesure est donc associée à un fait, c’est-à-dire une combinaison d’un membre de chaque dimension caractérisant le cube. Par exemple, le chiffre d’affaires (mesure) d’un magasin spécifique (membre de la dimension magasin) pour les produits alimentaires (membre de la dimension type de produit) au mois de septembre 2021 (membre du niveau mois de la dimension temporelle) constitue un fait d’un cube de données.

13Une interface dynamique OLAP permet aux utilisateurs finaux de naviguer librement dans les cubes de données en effectuant des opérations comme :

14• allouer des dimensions respectivement aux lignes et colonnes d’une table de pivot (tableau dynamique) (Gao et al., 2012) ;

15• allouer une mesure aux cellules d’une table de pivot ;

16• monter/descendre dans la hiérarchie d’une dimension à travers des forages (p. ex. passer des niveaux année à mois d’une dimension temporelle) et agréger les mesures en conséquence ;

17• filtrer les membres d’une dimension à travers des coupes (p. ex. ne considérer que les mesures attachées au mois novembre 2020 de la dimension temporelle).

C. SOLAP

18L’OLAP spatial (SOLAP) introduit la spatialisation des concepts OLAP pour une analyse à la fois multidimensionnelle et géographique (Bédard et Han, 2009). Ainsi, un cube de données spatiales inclut des dimensions spatiales dont les éléments (membres) sont associés à une géométrie vectorielle (Open Geospatial Consortium Inc., 2011). Par exemple, une dimension spatiale peut inclure des pays associés à des polygones géoréférencés. Ce type de dimension permet la représentation des données (mesures) dans des cartes interactives ainsi que des opérations de forages spatiaux à travers leurs niveaux hiérarchiques (p. ex. pays – région – province).

19De plus, le SOLAP peut bénéficier à la fois de l’analyse multidimensionnelle, fournie par l’OLAP, et de l’analyse spatiale, fournie par les SIG (Bimonte, 2008 ; Bimonte et al., 2010). Ces recherches proposent d’ailleurs le terme dimension géographique plutôt que dimension spatiale », car les membres de ces dimensions impliquent à la fois une définition thématique (p. ex. le pays Belgique) et une définition spatiale (p. ex. un polygone géoréférencé dont le contour représente la frontière belge). Le reste de cet article suit cette proposition.

20Le SOLAP peut être utile dans divers domaines tels que l’analyse des polluants, l’analyse de la criminalité, l’analyse des risques, la mobilité, la foresterie, les soins de santé, l’épidémiologie, etc. Néanmoins, certains domaines nécessitent des modèles SOLAP adaptés afin de répondre aux besoins de l’utilisateur. Ainsi, l’association habituelle d’entités vectorielles spatialement discrètes à des dimensions géographiques n’est pas adaptée aux applications nécessitant une vision continue de l’espace (Bimonte et Kang, 2010). Pour cette raison, une définition alternative des dimensions spatiales est proposée par (Kasprzyk 2015 ; Kasprzyk et Donnay, 2016) : les dimensions spatiales géographiques (à la fois thématiques et géométriques) restent des dimensions (S)OLAP classiques attachées aux entités spatiales (Bimonte, 2008) tandis que les dimensions spatiales géométriques (sans aspect thématique) sont les axes X et Y (éventuellement Z) d’un système de coordonnées de référence. Ainsi, un cube SOLAP caractérisé par des dimensions spatiales géométriques exploite des données raster combinées à des opérations d’algèbre de carte (Mennis et al., 2005) afin de gérer des champs continus dans l’analyse (Figure 2). La gestion des dimensions spatiales est donc assez différente entre un SOLAP vectoriel discret et un SOLAP raster continu.

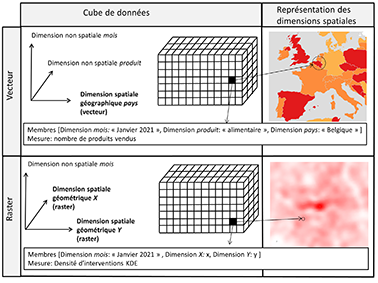
Figure 2. Comparaison des approches vectorielles et raster dans les cubes de données SOLAP

21L’outil OSCAR 1.0 a été développé selon un modèle SOLAP raster (Kasprzyk et Donnay, 2017) où un fait est un pixel associé à une valeur de densité KDE dépendant des dimensions spatiales planimétriques (X, Y), du type d’intervention, de l’heure de la journée et du jour de la semaine (Figure 1). En effet, du point de vue de l’utilisateur, un SOLAP agrégeant des faits KDE précalculés est plus performant qu’un SIG calculant des couches KDE à la volée sur base de très grands ensembles de points (Kasprzyk, 2015).

D. Métamodèles SOLAP

22Pour fonctionner avec plusieurs cubes de données, un outil SOLAP nécessite la définition des différents concepts manipulés au sein du système : cubes de données, dimensions, dimensions géographiques, hiérarchies, mesures, etc. Cette définition passe par un métamodèle (Boulil et al., 2011 ; Kasprzyk et Devillet, 2021 ; OMG, 2003) qui, une fois implémenté, permet le stockage de toutes les métadonnées des cubes afin de les explorer à travers les opérations SOLAP.

23D’une part, ces opérations peuvent être appliquées au sein d’un même cube par filtrage sur les membres de dimensions (coupes ou slices) ou par agrégation des données selon des dimensions représentées à différents niveaux de granularité (forages ou drill down). D’autre part, ces opérations peuvent impliquer plusieurs cubes partageant certains éléments (dimensions, mesures, etc.) et formant ainsi une constellation (Miquel et al., 2002). En effet, plusieurs cubes sont nécessaires pour stocker des informations hétérogènes, que ce soit pour des raisons thématiques (p. ex. données de sources différentes mais partageant certaines dimensions) ou dans un souci d’optimisation des performances du SOLAP (p. ex. stockage de données préagrégées selon des niveaux de dimensions moins détaillés).

24Les métamodèles autorisent des opérations dites interstellaires (Abelló et al., 2003), exploitant les liens sémantiques entre cubes pour la navigation dans une constellation ou même pour effectuer des comparaisons entre ces cubes (forage latéral ou drill across). En particulier, le métamodèle de Kasprzyk et Devillet (2021) est utilisé pour l’analyse géographique impliquant des dimensions hétérogènes. Ce métamodèle a été exploité dans un SOLAP vectoriel.

II. Hypothèse

25Rappelons que l’objectif de la recherche est l’amélioration de l’outil d’analyse de risque du SIAMU (OSCAR 1.0), initialement conçu comme un SOLAP raster analysant des champs KDE d’interventions. Dans le but de mieux interpréter les mesures KDE associées aux pixels des cubes de données, le SIAMU souhaite intégrer des mesures nombre d’interventions dans l’analyse des cartes de hotspots spatialement continues. De plus, cette analyse devrait également intégrer des entités géographiques discrètes telles que les secteurs d’interventions.  

26Pour atteindre cet objectif, l’approche la plus simple consisterait à intégrer une mesure nombre d’interventions (éventuellement dérivée par unité de surface) directement dans les cubes raster en plus de la mesure KDE. Cette solution permettrait de conserver un modèle raster unique pour l’outil OSCAR. Cependant, la précision géométrique de l’analyse des nombres d’interventions serait ainsi biaisée par la résolution spatiale des cubes raster d’OSCAR. Puisque les cartes KDE à la résolution de 50 mètres (associée à une fenêtre de lissage de 250 mètres) sont jugées pertinentes par les services d’urgence bruxellois, diminuer la résolution spatiale ne ferait qu’alourdir les traitements SOLAP pour une plus-value négligeable dans l’analyse spatialement continue.

27L’état de l’art nous a révélé qu’un modèle SOLAP vectoriel permettrait d’analyser les interventions agrégées selon des entités géographiques (p. ex. secteurs d’interventions) sans biais géométrique. Ainsi, notre hypothèse de recherche consiste à intégrer des cubes vectoriels et raster dans un modèle SOLAP hybride. Puisque l’analyse de cubes de données hétérogènes (vecteur et raster) se base sur une constellation, un métamodèle doit permettre une navigation cohérente via des opérations interstellaires dans cette constellation hybride. À notre connaissance, les métamodèles de la littérature SOLAP ne se sont jusque-là intéressés qu’à l’analyse de cubes vectoriels. Notre hypothèse repose donc également sur l’exploitation du métamodèle de Kasprzyk et Devillet (2021) jugé efficace pour l’analyse géographique impliquant des dimensions hétérogènes. Dans notre étude, cette hétérogénéité concernera les dimensions spatiales pouvant être thématiques (sur base vectorielle) ou non (sur base raster).

III. Cas d’étude

28Les missions du SIAMU comprennent à la fois l’aide médicale urgente, la lutte contre les incendies, et d’autres opérations de secours aux personnes. Nous ferons ici la distinction entre le risque jaune lié à l’aide médicale urgente et le risque rouge, lié aux opérations de secours et de lutte contre l’incendie.

29Les données utilisées pour peupler les cubes de données des risques récurrents rouge et jaune sont extraites de la base de données du logiciel de dispatching utilisé à la centrale d’urgence 112 de Bruxelles. La ou les catégorie(s) d’interventions définie(s) dans chaque fiche d’intervention créée au moment de l’appel d’urgence, ainsi que le type de moyens envoyés – envoi ou non d’un véhicule du Service Mobile d’URgence (SMUR) dans le cas des interventions médicales – sont utilisés pour classer chaque intervention de façon univoque dans l’une des six grandes catégories du tableau 1. Ces catégories correspondent effectivement aux membres de la dimension type_intervention décrites à la section IV-B-2.

Catégorie	Description
A1	Interventions d’aide médicale urgente nécessitant l’envoi d’une ambulance ou d’un PIT*
A2	Interventions d’aide médicale urgente nécessitant l’envoi supplémentaire d’un SMUR**
F1	Interventions d’incendie de niveau 1, nécessitant l’envoi de moyens limités
F2	Interventions d’incendie de niveau 2, nécessitant l’envoi de moyens importants
S1	Interventions de secours de niveau 1, nécessitant l’envoi de moyens limités
S2	Interventions de secours de niveau 2, nécessitant l’envoi de moyens importants

Tableau 1. Catégorie d’interventions
* PIT : Paramédical Intervention Team, ambulance dont l’équipage est complété par un(e) infirmier(ère) spécialisé(e) en soins d’urgence
** SMUR : Service Mobile d’Urgence, véhicule dont l’équipage est composé d’un binôme médecin + infirmier(ère), spécialisés en soins d’urgences

30Afin d’arriver le plus rapidement possible sur les lieux d’intervention, tout en évitant la saturation des postes de secours, la répartition des ressources humaines et matérielles peut ainsi être envisagée selon ces trois grandes dimensions:

31• une catégorie de risque récurrent (Tableau 1) conditionnant les types d’équipements et de personnel affectés aux postes de secours ;

32• un espace, pouvant être considéré de façon continue ou discrète, du point de vue du risque et de l’accessibilité des postes de secours (secteurs d’interventions) ;

33• un temps décomposé en plusieurs cycles: jour de la semaine, heure de la journée et période annuelle.

34Cette dimensionnalité est déduite des données d’interventions ainsi caractérisées par leur type, leurs coordonnées spatiales et leur date/heure. L’accessibilité des véhicules de secours, quant à elle, est déduite des emplacements des postes et d’un graphe routier OSM caractérisé par des vitesses de déplacement propres au SIAMU (Kasprzyk et Donnay, 2017). Elle est examinée séparément pour les ressources jaunes (lieux de départ des ambulances) et rouges (postes avancés d’incendie). En plus des secteurs d’interventions, l’analyse spatiale du risque récurrent intègre également certaines entités administratives bruxelloises (secteurs statistiques, quartiers statistiques et communes) pour être éventuellement comparée à d’autres données statistiques disponibles à ces niveaux.

IV. Méthodologie

A. Métamodèle

35La Figure 3 est une représentation du métamodèle de Kasprzyk et Devillet (2021) exploité dans cette étude. Il s’agit d’un diagramme de classes UML décrivant toutes les métaclasses du métamodèle ainsi que leurs associations. L’idée principale de ce métamodèle est de pouvoir générer une constellation de cubes de données, elle-même décrite par des schémas en étoile interconnectés (Kimball et Ross, 2013). Une instance du métamodèle est donc un modèle de cube de données vecteur ou raster.

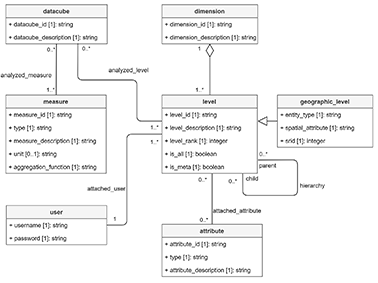
Figure 3. Métamodèle des cubes de données spatiaux

36La métaclasse principale datacube est directement associée à un ou plusieurs niveaux de dimensions (métaclasses level et dimension) afin de permettre une navigation dans la constellation à travers des opérations de forage interstellaire (drill down pour descendre ou roll up pour monter dans une hiérarchie).

37L’association récursive de la métaclasse level structure les niveaux d’une même dimension de manière hiérarchique pour les opérations de forage. Notons que les cardinalités de cette association autorisent les hiérarchies non strictes, c.-à-d. comprenant des niveaux enfants associés à plusieurs niveaux parents (Malinowski et Zimányi, 2004), ce qui constitue une des caractéristiques de la dimension géographique du SOLAP développé dans cette étude (voir section suivante).

38Puisqu’il s’agit d’un métamodèle SOLAP, les dimensions géographiques vectorielles sont gérées par la métaclasse geographic_level qui hérite des propriétés de level. Une instance de geographic_level est un niveau de dimension caractérisé par un attribut de type géométrie vectorielle, nécessaire pour sa représentation cartographique mais aussi pour la dérivation de mesures spatiales (p. ex. nombre d’incidents par km²). Chaque niveau, qu’il soit géographique ou non, peut être associé à plusieurs attributs définis par l’utilisateur (p. ex. population des communes). Notons qu’une dimension peut comprendre à la fois des niveaux géographiques et non géographiques, bien que seuls les niveaux géographiques puissent être cartographiés.

39La métaclasse measure instancie les différentes mesures agrégées dans les cubes de données. Dans la majorité des systèmes OLAP et SOLAP vectoriels, les mesures sont des valeurs numériques (entiers ou réels) agrégées par une somme. Dans des cas plus particuliers, la fonction d’agrégation (attribut aggregation_function de la métaclasse measure) peut être différente : concaténation de chaînes de caractères, comptage, moyenne, union de géométries, etc. C’est notamment le cas des modèles SOLAP raster (Kasprzyk, 2015) qui agrègent des mesures de type raster à travers des opérations locales d’algèbre de cartes (Mennis et al., 2005). La gestion de cubes de données raster à travers notre métamodèle implique donc l’exploitation d’un type raster comme propriété de la métaclasse measure, ainsi qu’une fonction d’agrégation locale par algèbre de cartes telle que définie par Kasprzyk (2015). Notons également que l’agrégation de mesures raster selon une dimension géographique est possible à travers une opération zonale d’algèbre de cartes, ce qui ne nécessite pas d’associations stricto sensu entre cubes raster et niveaux de dimensions géographiques dans les modèles instanciés (voir section suivante). 

40Un autre aspect original du SOLAP développé dans cette étude est la possibilité, pour l’utilisateur, de créer de nouveaux niveaux géographiques afin de les intégrer à la volée dans l’analyse. En effet, un membre de niveau géographique secteur_intervention correspond à une portion de territoire couverte par un poste de secours spécifique. Puisque ces secteurs sont calculés pour chaque utilisateur simulant diverses configurations d’emplacements de postes de secours, le métamodèle doit pouvoir associer certains niveaux de dimensions à l’analyse d’un utilisateur spécifique. Une métaclasse user est donc ajoutée au métamodèle de Kasprzyk et Devillet (2021) afin de tenir compte de cette particularité.

B. Constellation de cubes de données

1. Définition des cubes de données

41Sur base du métamodèle décrit précédemment, plusieurs cubes sont instanciés afin de proposer une analyse de risque fluide (c.-à-d. avec un temps de traitement rapide) et cohérente aux services d’urgence. La définition de ces cubes repose sur des critères à la fois thématiques (p. ex. interdiction d’agréger plusieurs fois le même incident) et techniques (p. ex. exploitation de cuboïdes pour éviter des temps de réponse trop longs) ayant nécessité plusieurs interactions avec les décideurs du projet OSCAR 2.0 dans la phase d’analyse des besoins.

42Du point de vue thématique, malgré leur source commune de données (base de données des incidents), les interventions rouges et jaunes sont stockées dans des cubes distincts pour deux raisons. D’une part, puisqu’elles nécessitent des ressources différentes (personnel et matériel), leurs analyses conjointes présentent peu d’intérêt pour les services d’urgence. D’autre part, un même incident peut nécessiter à la fois l’intervention des services médicaux et des pompiers. Cette séparation des cubes jaunes et rouges garantit donc de ne jamais agréger plusieurs fois le même incident lors de l’analyse des interventions.

43Du point de vue technique, la définition de la dimensionnalité des cubes de données doit tenir compte de temps de traitements raisonnables (moins de 30 secondes pour les requêtes les plus complexes) dans l’analyse de l’utilisateur. Ces temps de traitements dépendent du nombre maximum de faits détaillés à agréger lors des opérations de forage, un fait détaillé étant décrit par un membre du niveau le plus détaillé de chaque dimension. En théorie, le nombre de faits détaillés d’un cube est déduit du produit cartésien entre les niveaux détaillés de dimensions le caractérisant. Par exemple, un cube comptant 3 dimensions avec 10 membres détaillés (c.-à-d. les membres du niveau de dimension le plus fin) comportera 10³ faits détaillés théoriques (produit cartésien de 3 ensembles à 10 modalités). Puisque ce nombre croît exponentiellement avec le nombre de dimensions, un compromis doit être réalisé entre le niveau de détail de l’analyse et les performances du système.

44En ce qui concerne le compromis entre performance et niveau de détail, les cubes vectoriels sont généralement moins contraignants que les cubes raster en raison d’une gestion différente du problème de la faible densité. En effet, parmi l’ensemble des faits détaillés théoriques, les cubes vectoriels ne stockent que les faits détaillés non nuls (un fait nul n’étant associé à aucune mesure car celui-ci n’existe pas dans les données). En revanche tous les faits spatiaux nuls des cubes raster sont stockés dans les valeurs no data  des pixels. Pour être performant, un cube raster doit donc être relativement dense, c’est-à-dire ne pas stocker trop de « no data ». Puisque la proportion de faits nuls tend à augmenter avec le niveau de détail d’un cube, la densité d’un cube raster peut être augmentée de trois façons :

45• en réduisant le nombre de dimensions non spatiales ;

46• en réduisant le nombre de membres des dimensions non spatiales (p. ex. dimension temporelle comprenant 6 tranches de 4 heures au lieu de 24 tranches d’une heure) ;

47• en réduisant le nombre de membres spatiaux géométriques (pixels), c’est-à-dire en augmentant la taille des pixels (résolution spatiale) pour un territoire donné.

48Il est aussi possible d’optimiser les temps de traitements sur un cube de données sans réduire sa dimensionnalité. Cette méthode consiste à stocker différentes versions du cube (cuboïdes) préagrégeant les données selon différents niveaux non détaillés sur certaines dimensions. Lorsqu’on stocke un cuboïde pour chaque combinaison possible de forage sur les dimensions, on obtient un treillis du cuboïde (Mann et Phogat, 2020) dans lequel l’utilisateur navigue à travers des opérations de forage sans nécessiter le moindre calcul d’agrégation par le système. Bien que cette solution garantisse des performances optimales, elle peut nécessiter un espace de stockage très important puisque le nombre de cuboïdes croît exponentiellement avec le nombre de dimensions (produit cartésien des ensembles de niveaux par dimension). De plus, l’exploitation des cuboïdes limite les agrégations à celles prévues par les hiérarchies dimensionnelles lors de l’analyse. Par exemple, un cube peut être agrégé sur l’ensemble des membres de la dimension année (niveau le plus haut de la hiérarchie ou niveau all) mais il ne peut pas être agrégé sur deux années choisies librement par l’utilisateur (car aucun membre de niveau supérieur n’est strictement défini par ces deux années).

49Dans cette étude, une fois tous les compromis décidés sur la dimensionnalité des cubes raster (5 dimensions non spatiales pour une résolution spatiale de 50 mètres), le nombre de faits détaillés était encore trop élevé pour garantir des performances acceptables sur toutes les opérations de forage. Notre objectif de performance a donc été obtenu en exploitant un seul cuboïde préagrégeant les données d’interventions sur toutes les années (2018, 2019 et 2020). Ainsi, l’opération de forage la plus complexe agrège 50 millions de faits (ou pixels) sur le cuboïde plutôt que 150 millions de faits sur le cube de base.

2. Modèle en constellation

50La Figure 4 montre une partie de la constellation instanciée par le métamodèle. Il s’agit des cubes destinés à l’analyse du risque récurrent rouge (interventions de pompiers) qui intègrent à la fois les données raster KDE (densités d’interventions calculées par KDE) et vectorielles (nombres absolus d’interventions). En dehors du niveau de dimension type_intervention, les cubes rouges et jaunes sont caractérisés par la même dimensionnalité. Il n’est donc pas nécessaire de détailler les modèles jaunes en plus des rouges. En outre, puisque cet article se focalise sur la complémentarité des cubes vectoriels et raster, nous ne décrirons pas les modèles des cubes vectoriels plus détaillés qui ne permettent pas de comparaisons avec les cubes raster, ces comparaisons nécessitant une dimensionnalité similaire entre les cubes.

51La constellation de la Figure 4 est formalisée comme un diagramme de classes UML. Alors que le métamodèle était constitué de métaclasses, ce nouveau modèle est exclusivement composé de classes (les classes du modèle étant des instances des métaclasses du métamodèle). Un code couleur est utilisé afin de distinguer les différents éléments interprétés par l’analyse SOLAP (à ne pas confondre avec le code couleur des types d’interventions rouges et jaunes) :

52• les classes jaunes sont les cubes de données (ou tables de faits lorsqu’elles sont implémentées dans un système de gestion de base de données relationnel) ;

53• les classes bleues sont des niveaux de dimensions ;

54• la classe verte est un niveau géographique de dimension.

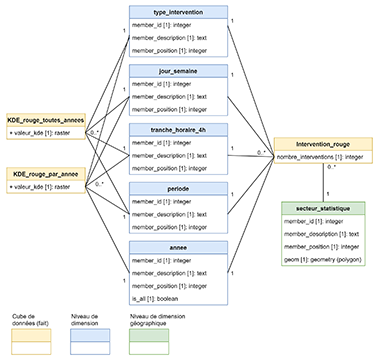
Figure 4. Constellation de cubes de données

55Dans un souci de simplification, la Figure 4 ne montre que les niveaux de dimensions détaillés, c’est-à-dire ceux directement associés au cube. Les six niveaux représentés (cinq non spatiaux et un géographique) appartiennent donc tous à des dimensions différentes et les résultats de l’analyse SOLAP peuvent être représentés selon n’importe laquelle de ces dimensions. Il est par exemple possible de créer un graphique des interventions par jour de la semaine, une carte des interventions par secteur statistique (niveau de dimension géographique), un tableau des interventions par type en rangées et tranche horaire en colonnes, etc. De plus, des opérations de coupe (slice) peuvent filtrer ces représentations selon n’importe quel membre de niveau de dimension, p. ex. la réalisation d’une carte des interventions par secteur statistique avec année = 2020 et type intervention = incendie.

56La constellation est composée de trois cubes : deux cubes raster à gauche et un cube vectoriel à droite. Ils sont modélisés par trois schémas en étoile partageant les niveaux de dimensions suivants : type_intervention, jour_semaine, tranche_horaire_4h et periode (la période distingue les mois de septembre à juin, des mois de juillet et août). Comme dans tout schéma en étoile, les instances des classes de cubes sont des faits détaillés associés à une mesure : valeur_KDE pour les cubes raster et nombre_interventions pour le cube vectoriel.

57En plus des quatre niveaux entièrement partagés par les trois cubes, le niveau de dimension année est partagé uniquement par le cube raster de base KDE_rouge_par_année et le cube vectoriel intervention_rouge. En effet, le cube raster KDE_rouge_toutes_années est le cuboïde préagrégeant les faits détaillés du cube raster de base selon le niveau all de la dimension année, et ses faits ne dépendent donc plus de cette dimension. Toutes les opérations de forage vers le niveau all de la dimension année impliquent donc une sélection de ce cuboïde par le système, alors que les opérations de forage vers le niveau détaillé année impliquent une sélection du cube de base KDE_rouge_par_année.

58Le niveau de dimension géographique secteur_statistique, quant à lui, n’est associé qu’au cube vectoriel puisque sa relation avec les cubes raster est obtenue par algèbre de cartes zonale. La représentation cartographique des cubes vectoriels exploite obligatoirement un des niveaux de la dimension géographique (voir section suivante) alors que celle des cubes raster exploite généralement les dimensions spatiales planimétriques X, Y définies implicitement dans les mesures raster (sauf cas particulier où le cube raster est agrégé par la dimension géographique).

59Avec ce modèle en constellation, toutes les opérations SOLAP de comparaisons sont permises entre les informations raster et vectorielles puisque ces deux types de cubes partagent bien toutes leurs dimensions non spatiales. L’utilisateur peut donc engendrer deux cartes avec une même opération SOLAP sur les dimensions non spatiales : une carte de hotspots calculée par KDE et une carte d’interventions agrégées par les entités de la dimension géographique. D’autres interactions entre cubes raster et vectoriels à travers des opérations SIG seront décrites dans la section V.

3. Dimension géographique

60La Figure 5 est une extension du diagramme de la Figure 4. Elle représente la dimension géographique complète du cube vectoriel (toujours selon le formalisme UML). Le niveau détaillé de cette dimension secteur_statistique (rang 0) est associé à tous les niveaux de rang 1, c.-à-d. quartier_statistique, commune et toutes les classes secteur_intervention associées à un utilisateur particulier (pour rappel, le niveau secteur_intervention dépend de la manière dont l’utilisateur a configuré la localisation des postes d’intervention). D’après cette modélisation, chaque membre d’entité vectorielle de rang 1 est l’union géométrique de membres du niveau secteur_statistique de rang 0. De la même manière, chaque membre du niveau région_bruxelloise_ou_province de rang 2 peut être strictement décomposé en membres d’un des niveaux de rang 1. Ainsi, des forages spatiaux peuvent être appliqués entre chaque niveau de rangs consécutifs et les mesures des faits résultant de ces forages sont agrégées à la volée pour les niveaux non détaillés (rangs 1 et 2).

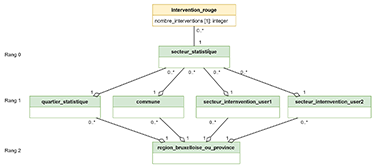
Figure 5. Dimension géographique des interventions

61Notons que le niveau région_bruxelloise_ou_province est défini par deux divisions administratives belges différentes: les régions et les provinces. Il comprend en réalité la région bruxelloise et les provinces belges situées dans son voisinage. Cette vision particulière des données provient du fait que la région bruxelloise ne comporte pas de province et que cette région est beaucoup moins étendue que les deux autres régions du pays (wallonne et flamande). Les services d’urgence bruxellois intervenant parfois dans les provinces voisines en raison du principe de l’aide adéquate la plus rapide (Service Public Fédéral Intérieur, 2012), cette modélisation permet d’intégrer l’ensemble des interventions avec une précision géométrique jugée suffisante pour celles situées en dehors de Bruxelles. Puisque la région bruxelloise est géométriquement dissociée des provinces, cela ne pose pas de problème de modélisation du point de vue du SOLAP. Notons que les couches raster KDE, quant à elles, ne concernent que la région bruxelloise.

C. Construction des secteurs d’interventions

62La construction des secteurs requiert l’utilisation d’un réseau arcs-nœuds (graphe) navigable. Dans notre cas, les données de voiries (OSM, 2021) ont été sélectionnées pour leurs excellents niveaux de complétude, leur topologie et la fréquence de mise à jour des sens de circulation pour la région bruxelloise.

63Le processus de calcul des secteurs d’interventions s’articule en trois étapes:

641. Pour chaque poste de secours : calcul du coût en chaque nœud du réseau. Ce coût correspond au temps de déplacement théorique le plus rapide depuis un poste (caserne ou point de départ ambulance) en utilisant l’algorithme de Dijkstra. Rappelons que ce calcul reste théorique dans la mesure où il dépend des vitesses de déplacement associées à chaque arc du réseau (Kasprzyk et Donnay, 2017).

652. Sélection en chaque nœud de l’identifiant du poste présentant le coût minimal.

663. Transformation de la couche de nœuds issue de l’étape 2 en une couche de polygones (c.-à-d. les secteurs d’interventions).

67Plusieurs méthodes sont possibles pour réaliser la transformation de l’étape 3. Compte tenu du contexte de l’outil SOLAP, la méthode sélectionnée consiste à utiliser la plus petite entité spatiale vectorielle disponible, c.-à-d. le secteur statistique, et de lui associer l’identifiant de la source considérée comme la plus proche. Il s’agit de celle qui est représentée par le plus grand nombre de nœuds de coût minimal dans le secteur statistique. Dans le cas hypothétique où un secteur statistique ne contiendrait aucun nœud, le mode des secteurs adjacents peut être choisi.

68Malgré l’imprécision – à un secteur statistique près – observée sur le calcul des secteurs d’interventions, cette méthode présente plusieurs avantages :

69• Temps de traitement court : pour rappel, la construction des secteurs d’interventions dépend de la localisation des sources (casernes ou points de départ ambulance) définies par l’utilisateur. Les secteurs d’interventions doivent donc être construits au vol dans un délai d’attente que l’utilisateur jugera acceptable.

70• Topologie correcte : le résultat remplit directement, sans nécessiter de post-traitement, la double condition topologique suivante : les bords des secteurs ne doivent pas se chevaucher ni laisser d’hiatus entre eux.

71• Bonne intégration dans le SOLAP vectoriel : le secteur d’intervention s’intègre naturellement dans la hiérarchie des différents niveaux géographiques du modèle de la Figure 5 et autorise les fonctionnalités de forage spatial depuis le niveau secteur_intervention vers le niveau secteur_statistique.

72D’autres méthodes ont été écartées. En calculant les enveloppes convexes ou concaves des nœuds associés à une même source, le résultat ne répond pas aux conditions topologiques attendues et nécessite un post-traitement supplémentaire. La fusion des polygones de Voronoï calculés autour de chaque nœud et associés à un même poste présente un temps de calcul trop long et le résultat ne s’intègre pas dans la hiérarchie spatiale des différentes entités géographiques vectorielles.

V. Interactions entre cubes vectoriels et raster

73La Figure 6 montre quelques exemples d’exploration cartographique du risque récurrent que permet l’outil final. Imaginons qu’un utilisateur souhaite analyser la répartition du risque récurrent lié aux interventions de secours de niveau 1-S1 (Tableau 1) dans une situation simulée où une nouvelle caserne de pompiers serait installée à l’emplacement de Forest-National (situé dans le secteur statistique de Forest). Des coupes sur la dimension temporelle ne sont pas considérées dans cet exemple.

74L’utilisateur positionne la nouvelle caserne et les secteurs d’interventions sont calculés au vol en tenant compte du nouvel emplacement. Leurs frontières peuvent être surimposées à une première carte de densité KDE du risque récurrent S1 (Figure 6-A) qui permet de repérer visuellement des zones de plus haute densité d’interventions (hotspots). Pour objectiver les valeurs de densité de la carte A, l’utilisateur peut réutiliser les mêmes paramètres d’analyse (c.-à-d. coupes sur les dimensions non spatiales) et afficher la carte B, en mode vecteur cette fois, qui représente une densité d’interventions par km² par secteur d’intervention. Notons que le nombre absolu d’interventions peut être également représenté dans une carte alternative, par exemple sous la forme de cercles de tailles proportionnelles aux nombres absolus d’interventions, centrés sur chaque entité. Pour des raisons de confidentialité des données, les classes de valeurs utilisées pour les cartes figurant dans cet article sont volontairement omises de la légende.

75Puisqu’il s’intéresse particulièrement au secteur de la caserne simulée de Forest, l’utilisateur peut alors réaliser un forage spatial dans ce secteur et obtenir les cartes C (en mode raster) et D (en mode vecteur). La palette de couleurs de la carte C est alors adaptée aux valeurs minimales et maximales de densité KDE de la zone, ce qui permet éventuellement de faire apparaître des hotspots qui n’étaient pas visibles dans la carte A. Dans le cas du forage spatial en mode vecteur, la carte D permet d’obtenir plus de détails sur le nombre d’interventions au niveau du secteur statistique dans le secteur d’intervention de Forest. L’utilisateur peut aussi analyser les autres dimensions (types de risques ou temps) sous formes graphiques ou tabulaires pour ce secteur particulier.

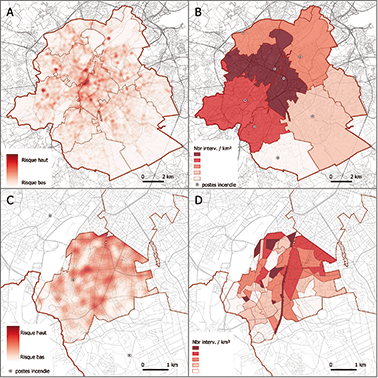
Figure 6. Exemples d’exploration cartographique du risque récurrent. (A) Densité d’interventions S1 par la méthode du KDE en région bruxelloise. (B) Densité d’interventions S1 par secteur d’intervention en région bruxelloise. (C) Densité d’interventions S1 par la méthode du KDE dans le secteur d’intervention de Forest. (D) Densité d’interventions par secteur statistique dans le secteur d’intervention de Forest.

76Il est également possible de connaître le nombre d’interventions concernées par un ou plusieurs hotspots KDE, qu’ils soient isolés d’une carte raster manuellement (détourage) ou automatiquement par classification en quantiles (Chainey, 2013). Un opérateur topologique d’intersection permet en effet d’inclure ces hotspots à la volée dans la hiérarchie d’une dimension géographique associée à un cube vectoriel spatialement plus détaillé, c’est-à-dire associé à un niveau géographique ponctuel tel que localisation_d’incident (dans un souci de concision, ces cubes vectoriels plus détaillés ne sont pas décrits dans cet article).

Conclusions

77Le SIAMU de Bruxelles s’étant doté en 2017 d’un outil SOLAP raster, appelé OSCAR, pour l’analyse du risque récurrent à travers des champs KDE, cette recherche a pour objectif d’améliorer cet outil en y intégrant l’analyse des nombres absolus d’interventions. Suite à un état de l’art portant sur l’analyse du risque ainsi que sur les outils BI et SOLAP, notre hypothèse de recherche consiste à combiner le modèle SOLAP raster spatialement continu d’OSCAR, avec un modèle SOLAP vectoriel exploitant des dimensions géographiques spatialement discrètes. 

78Afin de permettre des interactions, notamment par comparaisons et recoupements, entre cubes de données raster et vectoriels, l’outil est conceptualisé sur base d’un métamodèle unique (Kasprzyk et Devillet, 2021) permettant la navigation dans une constellation de cubes aux dimensions hétérogènes. Dans notre cas d’étude, cette hétérogénéité concerne les dimensions spatiales du SOLAP pouvant être géographiques (vectorielles) ou géométriques (raster). D’un côté, les cubes vectoriels comprennent une mesure entière nombre_interventions agrégée par une fonction somme. D’un autre côté, les cubes raster comprennent une mesure raster valeur_kde agrégée par une fonction locale d’algèbre de cartes. De plus, les cubes vectoriels sont intrinsèquement définis par au moins un niveau de dimension géographique, alors que les cubes raster peuvent être agrégés selon n’importe quel niveau de dimension géographique à travers une fonction zonale d’algèbre de cartes. 

79Avec une dimensionnalité commune relativement détaillée, l’agrégation des cubes raster s’avère moins performante que celles des cubes vectoriels. Afin de garantir une analyse SOLAP fluide, une décomposition des cubes raster en cuboïdes selon la dimension temporelle est proposée. Celle-ci conduit à une constellation hybride dont les métadonnées de navigation (cubes raster, cuboïdes raster et cubes vectoriels) et d’agrégation (mesures numériques ou raster) sont entièrement gérées par le même métamodèle. 

80L’outil OSCAR 1.0 permettait déjà à l’utilisateur de simuler différentes configurations de localisations de postes de secours pour analyser leur accessibilité. La nouvelle version OSCAR 2.0 intègre en outre un niveau de dimension géographique secteur_intervention définissant, pour chaque poste, le polygone dans lequel le poste en question serait le premier arrivé sur un lieu d’incident. Ces secteurs, générés à la volée par l’algorithme de Dijkstra sur un graphe routier OSM, sont intégrés dans la hiérarchie de la dimension géographique (secteur_statistique – secteur_intervention – région_bruxelloise_ou_province) et peuvent ainsi être exploités dans des forages spatiaux sur les cubes vectoriels ou raster.

81Pour terminer, un cas d’utilisation est présenté à travers différentes cartes montrant quelques opérations SOLAP tirant profit des interactions entre cubes vectoriels et raster. Du point de vue de l’analyse de risque, ces opérations permettent une visualisation cartographique du risque récurrent non biaisée par des frontières artificielles, combinée à une analyse précise du nombre d’interventions associées à des entités géographiques (secteurs d’interventions ou entités administratives). Bien que peu illustrées dans cet article, toutes les opérations OLAP sur les dimensions non spatiales sont permises par le métamodèle afin d’enrichir l’analyse du risque (p. ex. visualisation et forages des dimensions non spatiales).

82Du point de vue SOLAP, cette approche hybride ouvre la voie à d’autres applications pouvant nécessiter l’analyse multidimensionnelle conjointe de cubes vectoriels et raster. Par exemple, des modèles interpolant la qualité de l’air dans un espace continu sur base de capteurs in situ (Schneider et al., 2017) pourraient être ainsi confrontés, du point de vue multidimensionnel, à des données discrètes portant sur la population et/ou l’occupation du sol. 

83Bien entendu, notre méthodologie doit encore être validée par l’implémentation d’OSCAR 2.0 prévue pour la fin de l’année 2021. Cette implémentation exploitera notamment un entrepôt de données spatial PostGIS (PostGIS, 2021) pour le stockage des cubes et les requêtes d’agrégations, ainsi que l’extension pgRouting (pgRouting, 2021) pour les calculs d’accessibilité dans le graphe routier OSM. Le serveur SOLAP sera implémenté en exploitant le métamodèle géré par PostgreSQL (PostgreSQL Global Development Group, 2021) et plusieurs librairies JavaScript pour la représentation des dimensions spatiales (OpenLayers, 2021) et non spatiales (Chart.js, 2021).

Bibliographie

84Abelló, A., Samos, J. & Saltor, F. (2003). Implementing operations to navigate semantic star schemas. In Rizzi, S. et Song, I.Y. (eds), Proceedings of the 6th ACM International Workshop on Data Warehousing and OLAP  - DOLAP ’03. New Orleans : ACM Press, 56. https://doi.org/10.1145/956060.956071

85Badard, T., Dubé, E., Diallo, B., Mathieu, J. & Ouattara, M. (2009). Open source geospatial Business Intelligence (BI) in action. In Bocher, E. et Ertz, O. (eds), Abstract Proceedings of the Tenth International Opensource Geospatial Research Symposium, OGRS 2009. Paris : Publibook.

86Bédard, Y. & Han, J. (2009). Fundamentals of Spatial Data Warehousing for Geographic Knowledge Discovery. In Miller, H.J. et Han, J. (eds), Geographic Data Mining and Knowledge Discovery. 2e édition. Boca Raton (FL) : Chapman et Hall/CRC, 45-67.

87Bimonte, S. (2008). Intégration de l’information géographique dans les entrepôts de données et l’analyse en ligne : de la modélisation à la visualisation. Doctorat, Lyon, Institut National des Sciences Appliquées de Lyon, inédit, 219 p.

88Bimonte, S. & Kang, M.-A. (2010). Towards a Model for the Multidimensional Analysis of Field Data. In Catania, B., Ivanović, M., Thalheim, B. (eds.), Advances in Databases and Information Systems. Berlin, Heidelberg : Springer, Lecture Notes in Computer Science, 58-72. https://doi.org/10.1007/978-3-642-15576-5_7

89Bimonte, S., Tchounikine, A., Miquel, M. & Pinet, F. (2010). When Spatial Analysis Meets OLAP: Multidimensional Model and Operators. International Journal of Data Warehousing and Mining, 6, 33-60.

90Boulil, K., Bimonte, S. & Pinet, F. (2011). Un modèle UML et des contraintes OCL pour les entrepôts de données spatiales. De la représentation conceptuelle à l’implémentation. Ingénierie des systèmes d’information, 16, 11-39. https://doi.org/10.3166/isi.16.6.11-39

91Chainey, S. (2013). Examining the influence of cell size and bandwidth size on kernel density estimation crime hotspot maps for predicting spatial patterns of crime. Bulletin de la Société Géographique de Liège, 60, 7-19.

92Chart.js (2021). Chart.js Documentation. https://www.chartjs.org/docs/latest/. Consulté le 30 septembre 2021.

93Chevalier, P., Thomas, I., Geraets, D., Goetghebeur, E., Janssens, O., Peeters, D. & Plastria, F. (2012). Locating fire stations: An integrated approach for Belgium. Socio-Economic Planning Sciences, 46(2), 173-182.

94Gao, B., Zhang, S. & Yao, N. (2012). A Multidimensional Pivot Table Model Based on MVVM Pattern for Rich Internet Application. In 2012 International Symposium on Computer, Consumer and Control (IS3C). Taichung (Taiwan) : IEEE, 24-27. https://doi.org/10.1109/IS3C.2012.16

95Kasprzyk, J.-P. (2015). Intégration de la continuité spatiale dans la structure multidimensionnelle d’un entrepôt de données - SOLAP raster. Doctorat, Liège, Université de Liège, inédit, 299 p.

96Kasprzyk, J.-P. & Donnay, J.-P. (2016). A Raster SOLAP for the Visualization of Crime Data Fields. In Rückemann, C.-P. (ed.), Proceedings of GEOProcessing 2016. Venise : IARIA, 109–117.

97Kasprzyk, J.-P. & Donnay, J.-P. (2017). A Raster SOLAP Designed for the Emergency Services of Brussels Agglomeration. In CLOUD COMPUTING 2017. Athènes : IARIA, 32-38.

98Kasprzyk, J.-P. & Devillet, G. (2021). A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions. ISPRS International Journal of Geo-Information, 10, 87. https://doi.org/10.3390/ijgi10020087

99Kimball, R. & Ross, M. (2013). The data warehouse toolkit: the definitive guide to dimensional modeling, 3e édition. Indianapolis (IN): John Wiley et Sons, Inc. 567 p.

100Malinowski, E. & Zimányi, E. (2004). OLAP Hierarchies: A Conceptual Perspective. In King, R. (ed.), Active Flow and Combustion Control 2018. Berlin, Heidelberg : Springer, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 477-491. https://doi.org/10.1007/978-3-540-25975-6_34

101Mann, S. & Phogat, A.K. (2020). Dynamic construction of lattice of cuboids in data warehouse. Journal of Statistics and Management Systems, 23, 971-982. https://doi.org/10.1080/09720510.2020.1799498

102Mennis, J., Viger, R. & Tomlin, C.D. (2005). Cubic Map Algebra Functions for Spatio-Temporal Analysis. Cartography and Geographic Information Science, 32, 17-32. https://doi.org/10.1559/1523040053270765

103Miquel, M., Bédard, Y. & Brisebois, A. (2002). Conception d’entrepôts de données géospatiales à partir de sources hétérogènes. Exemple d’application en foresterie. Ingénierie des systèmes d’information, 7, 89-111. https://doi.org/10.3166/isi.7.3.89-111

104Negash, S. & Gray, P. (2008). Business Intelligence. In Burstein, F. et Holsapple, C.W. (eds), Handbook on Decision Support Systems 2. Berlin, Heidelberg: Springer, 175-193. https://doi.org/10.1007/978-3-540-48716-6_9

105OMG (2003). Common Warehouse Metamodel (CWM) Specification v 1.1. Object Management Group, 576 p. https://www.omg.org/spec/CWM/1.1/PDF. Consulté le 30 septembre 2021.

106Open Geospatial Consortium Inc. (2011). OpenGIS® Implementation Standard for Geographic information - Simple feature access - Part 1: Common architecture. 28-05-2011. OGC 06-103r4

107OpenLayers (2021). OpenLayers – Documentation. https://openlayers.org/en/latest/doc/. Consulté le 30 septembre 2021.

108OSM (2021). OpenStreetMap. https://www.openstreetmap.org. Consulté le 30 septembre 2021.

109pgRouting (2021). pgRouting Manual (3.2). https://docs.pgrouting.org/3.2/en/index.html. Consulté le 30 septembre 2021.

110PostGIS (2021). PostGIS 3.1.5dev Manual. https://postgis.net/stuff/postgis-3.1.pdf. 846 p. Consulté le 30-09-21.

111PostgreSQL Global Development Group (2021). PostgreSQL 14.0 Documentation, 2785 p. https://www.postgresql.org/files/documentation/pdf/14/postgresql-14-A4.pdf. Consulté le 30 septembre 2021.

112Schneider, P., Castell, N., Vogt, M., Dauge, F.R., Lahoz, W.A. & Bartonova, A. (2017). Mapping urban air quality in near real-time using observations from low-cost sensors and model information. Environment International, 106, 234-247. https://doi.org/10.1016/j.envint.2017.05.005

113Service Public Fédéral Intérieur (2007). 15 MAI 2007. - Loi relative à la sécurité civile (1). Moniteur Belge, le 31 juillet 2007, 40379-40409.

114Service Public Fédéral Intérieur (2012). 10 NOVEMBRE 2012. - Arrêté royal déterminant les conditions minimales de l’aide adéquate la plus rapide et les moyens adéquats. Moniteur Belge, le 27 novembre 2012, 71819- 71827.

115Service Public Fédéral Intérieur (2013). 14 OCTOBRE 2013. - Arrêté royal fixant le contenu et les conditions minimales de l’analyse des risques visée à l’article 5, alinéa 3, de la loi du 15 mai 2007 relative à la sécurité civile. Moniteur Belge, le 30 octobre 2013, 83039-83044.

Pour citer cet article

A propos de : Jean-Paul KASPRZYK

A propos de : Nadia Poncelet