Matthieu LONCHAY & René WARNANT

Intégration de cartes de scintillations ionosphériques dans les algorithmes de positionnement par satellites

Résumé

Grâce au développement de plusieurs systèmes globaux de positionnement et de navigation par satellites, i.e. les Global Navigation Satellite Systems (GNSSs), les utilisateurs de ces systèmes bénéficient désormais de performances très élevées en termes d’exactitude, de continuité et de fiabilité. Cependant, ces performances sont limitées, parfois de manière drastique, par l’ionosphère. En effet, la présence d’électrons libres dans l’ionosphère provoque des effets de réfraction et de diffraction des signaux électromagnétiques émis par les satellites des différentes constellations GNSS (GPS, GLONASS, Galileo, etc.). En particulier, des irrégularités dans la densité en électrons libres de l’ionosphère peuvent produire de fortes variations spatiotemporelles de l’indice de réfraction du milieu. Les signaux GNSS qui traversent de telles irrégularités ionosphériques sont susceptibles d’être affectés par de rapides fluctuations de leur phase et de leur amplitude désignées sous le terme de scintillations. Les scintillations ionosphériques peuvent anéantir totalement les performances de positionnement et de navigation des GNSSs. Elles sont particulièrement fréquentes dans les régions polaires et équatoriales de la Terre.

Abstract

The ionosphere has always been a major limitation for the navigation and positioning performances of Global Navigation Satellite Systems (GNSSs). Free electrons in the ionosphere perturb the propagation of GNSS radio signals by involving refraction and diffraction effects. In particular, small-scale ionospheric irregularities can cause scattering effects on GNSS signals which result in rapid fluctuations of the signal phase and amplitude, also referred to as scintillations. Scintillations of GNSS signals can dramatically jeopardise the positioning performances of Single-Point Single-Epoch (SPSE) GNSS algorithms such as the Standard Point Positioning (SPP) and the Precise Point Positioning (PPP) algorithms.

Table des matières

Introduction

1Les Global Navigation Satellite Systems (GNSSs) sont des systèmes de positionnement et de navigation par satellites qui offrent une couverture globale dans le temps et dans l’espace. Actuellement, ces systèmes occupent une position déterminante dans notre société moderne car ils contribuent directement ou indirectement et de façon significative au fonctionnement de multiples applications associées à différents secteurs d’activité économique mondiale. À cet instant même, des millions de récepteurs GNSS sont exploités dans le monde entier par un large éventail d’applications industrielles, scientifiques, militaires et civiles. Ces applications concernent, par exemple, les smartphones géolocalisés, le contrôle de véhicules autonomes, les levés topographiques par drones ou encore l’agriculture de précision. Elles reposent sur différentes techniques de navigation et de positionnement basées sur différents algorithmes GNSS en fonction des performances requises.

2Les performances des systèmes de positionnement par satellites sont tributaires de nombreuses sources d’erreur. En particulier, les signaux GNSS peuvent souffrir d’effets de réfraction et de diffraction lors de leur propagation à travers l’ionosphère terrestre qui sont susceptibles de dégrader considérablement les performances des algorithmes de positionnement par satellites et de perturber les applications qui y sont associées. L’ionosphère constitue une région de l’atmosphère terrestre dans laquelle l’ionisation est suffisamment importante que pour affecter la propagation des signaux radio (Davies, 1990). Dans certaines conditions, l’apparition d’irrégularités dans la densité en électrons libres de l’ionosphère peut générer de fortes variations spatiotemporelles de l’indice de réfraction ionosphérique. Ce phénomène entraîne une diffraction des signaux GNSS qui se traduit par de rapides fluctuations de la phase et de l’amplitude des signaux GNSS lors de leur réception par un utilisateur, désignées sous le terme de scintillations ionosphériques. Ces scintillations ionosphériques apparaissent principalement dans les régions polaires et intertropicales. Dans ces régions, l’intensité des scintillations ionosphériques peut totalement annihiler les performances des systèmes de positionnement par satellites. Tandis que les applications modernes sont associées à des exigences de performance toujours plus élevées, l’atténuation des effets néfastes des scintillations ionosphériques pour le positionnement et la navigation par satellites reste un véritable défi pour les fabricants de récepteurs GNSS et la communauté scientifique.

3La recherche associée à cet article vise tout d’abord à démontrer la pertinence de l’utilisation de méthodes d’analyse spatiale afin de quantifier les caractéristiques spatiotemporelles des scintillations ionosphériques équatoriales. Grâce à l’utilisation de techniques d’analyse spatiale, le premier objectif de cette recherche est de concevoir des cartes du ciel, désignées sous le terme de skymaps, qui représentent l’intensité des scintillations ionosphériques à un instant donné. Ensuite, cette recherche consiste à prototyper des techniques de correction basée sur l’intégration de skymaps de scintillations ionosphériques. Ces techniques de correction doivent permettre d’améliorer les performances de certains algorithmes de positionnement par satellites en cas de scintillations ionosphériques. Tout particulièrement, cette recherche se focalise sur deux algorithmes GNSS : le Standard Point Positioning (SPP) et le Precise Point Positioning (PPP).

4Cet article débute par une brève présentation générale des algorithmes de positionnement par satellites et des scintillations ionosphériques. Ensuite, il présente une analyse symptomatique des effets des scintillations ionosphériques au sein des algorithmes GNSS. Cette analyse est suivie d’une section consacrée à l’application de techniques d’analyse spatiale à des mesures de scintillations ionosphériques effectuées par des récepteurs de type ISMR (Ionospheric Scintillation Monitoring Receiver). Cette section vise, en particulier, à détecter la présence d’autocorrélation spatiale globale et locale dans des échantillons spatiaux expérimentaux constitués de skyplots. Ces échantillons sont constitués d’une série de points de mesure localisés dans un système de coordonnées horizontales centré sur la position d’un observateur, d’où l’utilisation du terme anglais skyplot. Cette analyse aboutit à la construction de skymaps de scintillations ionosphériques. Enfin, la dernière section de cet article porte sur le prototypage de plusieurs stratégies qui visent à réduire les effets néfastes des scintillations ionosphériques sur les performances des algorithmes SPP et PPP en termes d’exactitude, de continuité et de fiabilité. Ces stratégies sont basées sur l’exploitation de l’information spatiotemporelle contenue dans les skymaps de scintillations ionosphériques élaborées pour chaque époque d’observation. Ces stratégies, implémentées en tant que prototypes au sein d’un logiciel de positionnement GNSS existant, impliquent l’intégration continue de skymaps de scintillations ionosphériques au sein des algorithmes SPP et PPP. Cette dernière section se termine par une comparaison des différents types de stratégies d’atténuation développées dans le cadre de cette recherche.

I. Positionnement GNSS

5Le positionnement par satellites est basé sur le principe de multilatération. Afin de déterminer sa position, un récepteur GNSS effectue des mesures simultanées sur les signaux émis par plusieurs satellites GNSS en orbite autour de la Terre. Désormais, le positionnement par satellites peut compter sur la disponibilité de multiples signaux associés à plusieurs fréquences dans la bande L émises par des satellites GNSS appartenant à plusieurs systèmes tels que GPS, GLONASS, Galileo ou encore BeiDou. Les mesures brutes effectuées par un récepteur sur des signaux GNSS incluent des mesures de pseudo-distance, effectuées sur les codes pseudo-aléatoires qui modulent les ondes porteuses, et des mesures de phase effectuées directement sur les ondes porteuses émises par les différents satellites GNSS. Ces mesures sont effectuées par le processeur de signal numérique (DSP – Digital Signal Processor) du récepteur, aussi appelé communément tracker dans la littérature anglophone, qui verrouille les différents signaux grâce à ses boucles à verrouillage de retard (DLL – Delay Lock Loop) et de phase (PLL – Phase Lock Loop).

6Les satellites GNSS émettent des codes pseudo-aléatoires uniques qui modulent les fréquences porteuses. Ces codes permettent à un récepteur GNSS de mesurer le temps de propagation des signaux GNSS grâce à une technique de corrélation croisée qui consiste à comparer le signal reçu avec un signal identique généré localement par le récepteur. L’équation 1 décrit le modèle mathématique d’une mesure de code, notée P^s_r,f, effectuée par un récepteur r sur un code modulant une onde porteuse de fréquence f émise par un satellite s. Ce modèle inclut la distance géométrique réelle entre le récepteur et le satellite, notée P^s_r, ainsi qu’une série de termes associés à plusieurs sources d’erreur. Ces sources d’erreur incluent les erreurs d’horloge du récepteur et du satellite par rapport à l’échelle de temps globale GNSS, notées respectivement δt_r et δt^s, les délais engendrés par la propagation du signal dans la troposphère et l’ionosphère, notés T^s_r et I^s_r,f,P respectivement, l’effet de multitrajet noté M^s_r,f,P, la combinaison des délais hardware dans les circuits électroniques du satellite et du récepteur, notés B^s_r,f,P et le bruit de mesure noté ε^s_r,f,P. La mesure de pseudo-distance modélisée par l’équation 1 s’exprime en unités de distance et les multiples indices en exposant et en indice révèlent les dépendances des termes d’erreur au récepteur r, au satellite s, à la fréquence f.

7Les distances géométriques entre un récepteur et un satellite GNSS peuvent également être estimées à partir de mesures de phase effectuées directement sur les ondes porteuses. L’équation 2 décrit la modélisation mathématique d’une mesure de phase, notée Ф^s_r,f, en utilisant le même système de notation que l’équation 1. Les termes additionnels N^s_r,f et φ^s_r,f représentent l’ambiguïté entière initiale et l’erreur de phase wind-up exprimée en cycles, respectivement. Le terme λ_f symbolise la longueur d’onde correspondant à la fréquence f exprimée en mètres.

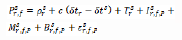
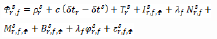
8Les mesures de phase sont deux ordres de grandeur plus précis que les mesures de code, mais elles comportent un terme ambigu additionnel. En effet, en raison de la nature sinusoïdale des ondes porteuses, chaque mesure de phase est associée à un nombre entier inconnu de cycles, soit un nombre entier d’oscillations de l’onde entre la position du satellite et la position du récepteur. Ce nombre entier est désigné sous le terme ambiguïté entière initiale noté N^s_r,f dans l’équation 2. La valeur de l’ambiguïté entière initiale s’ajoute aux autres inconnues à estimer mais elle reste constante tant que le signal associé reste verrouillé par le tracker du récepteur. En cas d’interruption suivie d’une nouvelle acquisition du signal, l’ambiguïté entière initiale change de valeur. Ceci implique que les algorithmes de positionnement par satellites qui exploitent la haute précision des mesures de phase peuvent atteindre des performances plus élevées à condition d’implémenter des techniques spécifiques de calcul qui permettent de déterminer la valeur des ambiguïtés entières initiales pour les différentes fréquences et satellites (Hofmann-Wellenhof et al., 2008 ; Leick et al., 2015 ; Subirana et al., 2013).

9Le fonctionnement d’un algorithme de positionnement par satellites est constitué de quatre étapes successives. Le modèle mathématique (i) décrit les relations mathématiques qui existent entre les observations et les paramètres inconnus à estimer. Le modèle mathématique d’un algorithme de positionnement par satellites peut être basé sur des mesures GNSS brutes ou sur des combinaisons de mesures GNSS brutes afin de s’affranchir partiellement ou totalement de certaines sources d’erreur. Le modèle stochastique (ii) décrit la précision originale des observations qui dépend de la précision des mesures effectuées par le récepteur GNSS. Il est principalement constitué de la matrice des variances-covariances des observations qui quantifient la précision absolue de chaque observation mais aussi les potentielles corrélations entre les observations. Le processus d’estimation des paramètres inconnus (iii) consiste à résoudre le système d’équations observationnelles en estimant les valeurs et la matrice de variances-covariances des paramètres inconnus. Enfin, le contrôle d’intégrité (iv) consiste en une batterie de tests statistiques qui permettent d’évaluer la validité de la solution calculée.

A. Standard Point Positioning (SPP)

10L’algorithme SPP est l’algorithme GNSS le plus simple mis en œuvre dans la plupart des récepteurs GNSS bas de gamme, tels que les récepteurs intégrés dans les smartphones, les montres de sport et les systèmes de navigation automobile. Il s’agit d’un algorithme de positionnement absolu qui ne nécessite pas de mesures effectuées par une station de référence ni de corrections calculées au sein d’un réseau géodésique. Cette particularité lui confère une grande autonomie et une bonne polyvalence. L’algorithme SPP exploite uniquement des mesures de code effectuées sur une seule fréquence. La précision de l’algorithme SPP est généralement comprise entre 1 m et 10 m, comme l’illustre la Figure 1. Elle est principalement affectée par la qualité de la géométrie satellitaire qui régit la propagation des erreurs entre les observations, i.e. les mesures GNSS brutes, et la solution, i.e. l’estimation de la valeur des paramètres inconnus qui incluent les coordonnées de position du récepteur. En outre, la précision de l’algorithme SPP est limitée par la qualité des éphémérides qui permettent de déterminer la position des satellites au moment de l’émission des signaux ainsi que par la précision des modèles atmosphériques utilisés pour modéliser les délais troposphériques et ionosphériques (Subirana et al., 2013).

11Le modèle mathématique de l’algorithme SPP est basé sur l’équation 1. Généralement, quatre paramètres inconnus sont considérés, à savoir les trois coordonnées de position et l’erreur d’horloge du récepteur. Par conséquent, un modèle mathématique constitué de minimum quatre mesures de code associées à quatre satellites distincts est nécessaire afin d’estimer la valeur des quatre paramètres inconnus. Les coordonnées de position du récepteur sont incluses dans le terme ρ^s_r qui représente la distance géométrique entre le récepteur et le satellite dans l’équation 1, ce qui nécessite une linéarisation préalable du modèle. Le modèle stochastique de l’algorithme SPP est généralement très basique. Dans sa version la plus simple, il considère que les mesures de code associées aux différents satellites observés ne sont pas corrélées et sont de précision identique, i.e. que leurs variances sont égales. Un modèle plus élaboré consiste à utiliser une pondération des mesures en fonction de l’élévation du satellite ou du rapport signal sur bruit associé. L’algorithme SPP implémente généralement une technique classique d’ajustement par moindres carrés afin d’estimer les valeurs et la matrice de variances-covariances des paramètres inconnus. En fonction des ressources de calcul disponibles et du type de récepteur GNSS, l’algorithme SPP peut également implémenter une technique de contrôle d’intégrité qui consiste à tester statistiquement la solution estimée et les résidus ajustés des différentes mesures de code (Baarda, 1967). Le contrôle d’intégrité peut également inclure un processus d’exclusion de mesures erronées qui, lors d’un échec des tests statistiques, va recalculer une solution en excluant une ou plusieurs mesures suspectes. Ce mécanisme est désigné sous le terme RAIM (Receiver Autonomous Integrity Monitoring) (Takasu, 2016). Étant donné que le contrôle d’intégrité est basé sur les résidus ajustés des observations, la validité du contrôle d’intégrité est fortement dépendante de la validité du modèle stochastique utilisé pour modéliser la précision originale des observations (Luo et al., 2009 ; Li et al., 2016).

B. Precise Point Positioning (PPP)

12L’algorithme PPP est un algorithme GNSS avancé implémenté dans les récepteurs GNSS haut de gamme et les logiciels de positionnement géodésiques. C’est une technique de positionnement absolu qui rivalise avec les techniques de positionnement relatif, telles que le RTK (Real Time Kinematic), en fournissant des solutions de positionnement en temps réel avec une précision centimétrique à décimétrique, comme l’illustre la Figure 1. Par rapport à l’algorithme RTK, l’algorithme PPP présente l’avantage de ne pas nécessiter de mesures effectuées par une station de référence ou un réseau de stations de référence. Ceci lui confère une grande autonomie, ce qui rend l’algorithme PPP très intéressant pour des applications opérant dans des régions dépourvues d’infrastructures. Néanmoins, pour atteindre de telles performances de positionnement, l’algorithme PPP s’appuie sur des corrections globales ou régionales qui permettent de s’affranchir partiellement ou totalement de certaines sources d’erreurs qui limitent généralement les performances d’algorithmes plus simples tels que le SPP.

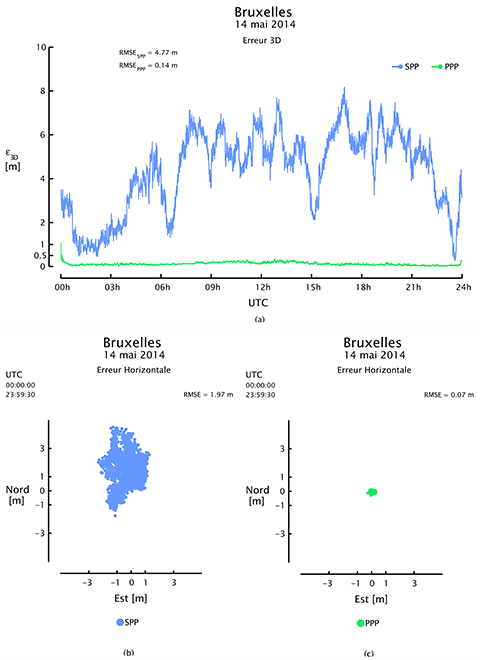
Figure 1. Précision et exactitude des algorithmes de positionnement par satellites de type SPP (bleu) et PPP (vert). Les valeurs représentées sur cette figure ont été obtenues pour la station de l’International GNSS Service (IGS) située à Bruxelles (BRUX) lors de la journée du 14 mai 2014 et en utilisant le logiciel de positionnement GNSS RTKLIB. (Dow et al., 2009 ; Takasu, 2013).

13La toute première définition spécifie que l’algorithme PPP est basé sur un modèle mathématique composé de combinaisons Ionosphere-Free formées de mesures de code ou de phase effectuées sur deux fréquences distinctes. Ces combinaisons, bien connues dans le domaine des GNSSs, ont l’avantage de faire disparaitre les termes d’erreur liés aux délais ionosphériques affectant les mesures de code ou de phase. Cependant, au cours des deux dernières décennies, la communauté scientifique a été témoin de nombreuses innovations concernant la disponibilité de multiples constellations, fréquences, observables et fournisseurs de corrections. Il en a résulté de nombreuses variantes de l’algorithme PPP original qui conduisent parfois à une confusion dans la littérature. Généralement, le processus d’estimation des paramètres inconnus de l’algorithme PPP est basé sur un filtre de Kalman qui, typiquement, combine les observations effectuées avec une prédiction de la valeur des paramètres inconnus. Cette prédiction est basée sur la valeur précédemment connue des paramètres inconnus et sur un modèle de bruit. Le nombre de paramètres inconnus à estimer de l’algorithme PPP est bien plus élevé que pour l’algorithme SPP, et cela nécessite d’ailleurs une puissance de calcul plus élevée. En plus des coordonnées de position et de l’erreur d’horloge du récepteur, l’algorithme PPP estime également la valeur du délai troposphérique ainsi que les ambiguïtés associées aux différentes fréquences et satellites impliqués. En conséquence, l’algorithme PPP est caractérisé par une période de convergence afin d’atteindre ses performances optimales en termes de précision et d’exactitude. Certaines versions plus avancées de l’algorithme PPP exploitent des techniques spécifiques afin de résoudre les ambiguïtés entières initiales, ce qui contribue à réduire la période de convergence de l’algorithme PPP (Wübbena, 1985 ; Zumberge et al., 1997 ; Héroux et Kouba, 2001 ; Laurichesse et al., 2009 ; Choy et al., 2017 ; Deo et El-Mowafy, 2016).

II. Scintillations Ionosphériques

14Davies (1990) définit l’ionosphère de la façon suivante : « the ionosphere constitutes a region of the Earth’s atmosphere where sufficient ionisation can exist to affect the propagation of radio signals ». L’ionosphère terrestre est comprise entre environ 60 km et 1000 km d’altitude. Il s’agit d’un plasma composé d’électrons libres et d’ions positifs. L’existence de l’ionosphère résulte de l’ionisation des composants de l’atmosphère par le rayonnement solaire. Sa morphologie est largement influencée par le champ magnétique terrestre. L’ionosphère est un milieu qualifié de dispersif qui se caractérise par un indice de réfraction vis-à-vis des signaux qui la traversent qui dépend de la fréquence.

15Lors de la traversée de l’ionosphère, les signaux GNSS subissent des effets de réfraction et de diffraction qui détériorent la qualité des mesures effectuées par un récepteur GNSS et, par conséquent, les performances en termes de positionnement. La réfraction ionosphérique dépend de la fréquence des signaux mais aussi de la densité en électrons libres de la partie de l’ionosphère traversée. En particulier, des irrégularités locales dans la densité en électrons libres de l’ionosphère engendrent une forte variabilité spatiotemporelle de son indice de réfraction. Lorsque des signaux GNSS traversent de telles irrégularités, ils subissent un effet de dispersion (scattering) résultant de multiples effets de réfraction. Ce phénomène génère, au niveau du récepteur, une figure de diffraction avec des interférences constructives et destructives entre les signaux directs et réfléchis, comme l’illustre la Figure 2. Ce phénomène conduit à de rapides fluctuations de l’amplitude et de la phase des signaux GNSS, désignées sous le terme de scintillations ionosphériques. La Figure 3 illustre des scintillations d’amplitude et de phase observées sur la fréquence GPS L1 pour le satellite G01 à la station d’Inconfidentes, au Brésil. Bien que le terme scintillations décrive les effets observés sur les signaux GNSS, son utilisation est fréquemment étendue afin de désigner également les irrégularités ionosphériques à l’origine des scintillations des signaux (Kintner el al., 2009).

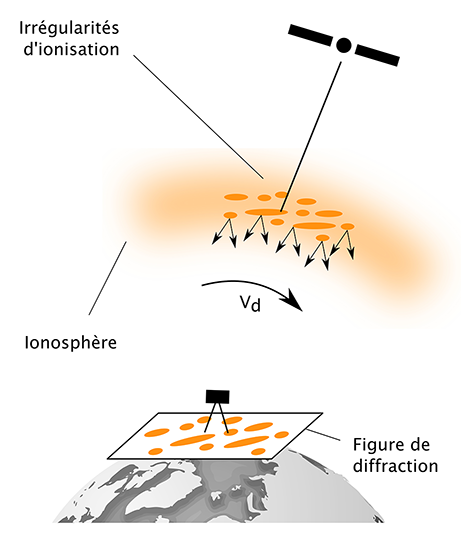
Figure 2. Scintillations ionosphériques. Les irrégularités locales dans la densité en électrons libres de l'ionosphère engendrent de fortes variations spatiotemporelles de l’indice de réfraction ionosphérique. Lorsque des signaux GNSS traversent de telles irrégularités, ils subissent un effet de dispersion (scattering) résultant de multiples effets de réfraction. Ce phénomène génère, au niveau du récepteur, une figure de diffraction avec des interférences constructives et destructives entre les signaux directs et réfléchis. Ce phénomène conduit à de rapides fluctuations de l’amplitude et de la phase des signaux GNSS, désignées sous le terme de scintillations ionosphériques.

16Plusieurs paramètres existent afin de mesurer l’intensité des scintillations ionosphériques affectant les signaux GNSS. Ces paramètres peuvent être calculés et fournis directement par les récepteurs de type ISMR qui sont capables d’effectuer des mesures sur les signaux GNSS à très haute fréquence (50 Hz-100 Hz). En particulier, l’indice S₄ est défini comme le coefficient de variation de l’intensité d’un signal sur un intervalle de temps donné, noté I dans l’équation 3. Dans le cadre de cette étude, l’intervalle de temps utilisé pour calculer cet indice est de 60 s. Les scintillations de forte amplitude ayant des répercussions sévères sur le positionnement GNSS sont généralement associées à des valeurs de l’indice S₄ supérieures à 0.6, tandis que la valeur de 0.3 constitue un seuil en-dessous duquel il est très peu probable que les utilisateurs de GNSS subissent des perturbations significatives. L’indice de scintillation d’amplitude S₄ constitue la principale variable utilisée dans le cadre de cette recherche et, en particulier, il est extensivement exploité pour l’application des techniques d’analyse spatiale qui conduisent à l’élaboration de skymaps de scintillations ionosphériques.

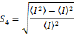
17Les analyses statistiques révèlent que les scintillations ionosphériques des signaux GNSS se rencontrent principalement dans les régions polaires et intertropicales de la Terre (Kintner et al., 2007 ; Lassudrie-Duchesne et al., 2010 ; SBAS Ionospheric Working Group, 2010). Cet article porte sur les scintillations ionosphériques équatoriales. Dans la région intertropicale, i.e. à proximité de l’équateur géomagnétique, les irrégularités ionosphériques sont principalement associées aux mécanismes de l’anomalie ionosphérique équatoriale (EIA - Equatorial Ionospheric Anomaly). Dans cette région du globe et durant le jour, le champ électrique Ouest-Est généré par la région E de l’ionosphère est perpendiculaire au champ magnétique terrestre qui est horizontal à proximité de l’équateur géomagnétique. En conséquence, le plasma ionosphérique de la région F de l’ionosphère est entraîné vers le haut à des altitudes plus élevées, ce qui est généralement décrit comme un effet fontaine dans la littérature. Le plasma ionosphérique se propage ensuite vers le Nord et vers le Sud, soit le long des lignes du champ magnétique terrestre, ce qui conduit à la formation de deux crêtes de forte ionisation de part et d’autre (environ 10°-20°) de l’équateur géomagnétique. Durant les heures qui suivent le coucher du soleil et l’arrêt du processus d’ionisation de la haute atmosphère par le rayonnement solaire, on observe des instabilités dans la région F de l’ionosphère. Les processus de recombinaison prennent le pas sur les processus d’ionisation, ce qui entraîne la présence de couche de faible densité situées sous des couches ionisées. Des instabilités ionosphériques de type Rayleigh-Taylor apparaissent et on observe la formation de structures désignées sous les termes bubbles ou plumes dans la littérature anglophone. Il s’agit de trous dans la densité en électrons libres de l’ionosphère qui se forment à la base de la région F de l’ionosphère et qui s’élèvent ensuite en altitude en traversant verticalement la région F de l’ionosphère. Ces structures ont typiquement une taille d’environ 100 km et perdurent pendant environ 2 ou 3 heures, du coucher de soleil jusqu’à peu près minuit local, mais leur extension spatiale peut s’étendre de quelques centimètres à plusieurs dizaines de kilomètres et leur extension temporelle de quelques secondes à plusieurs heures. Ces irrégularités dans la densité en électrons libres de l’ionosphère sont responsables de scintillations fréquentes et intenses des signaux GNSS dans cette région de la Terre.

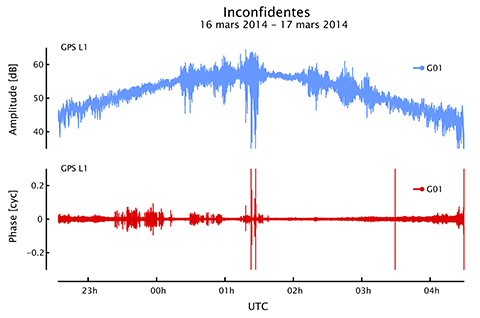
Figure 3. Les scintillations d'amplitude et de phase du signal GPS L1 pour le satellite G01 observées depuis une station ISMR (Ionospheric Scintillation Monitoring Receiver) située à Inconfidentes au Brésil en mars 2014

III. Effets des scintillations ionosphériques sur les GNSS

18Au-delà des fluctuations rapides de la phase et de l’amplitude des signaux GNSS, les scintillations ionosphériques sont à l’origine de dégradations sévères des performances des algorithmes de positionnement par satellites en termes d’exactitude, de continuité et de fiabilité. En particulier, des signaux GNSS affectés par des scintillations ionosphériques intenses peuvent empêcher le tracker des récepteurs GNSS de maintenir le verrouillage sur les signaux, ce qui conduit à des pertes de signal et à une dégradation de la qualité de la géométrie satellitaire. En outre, ces pertes de signal peuvent également déstabiliser les processus d’estimation basés sur des filtres et provoquer des périodes de convergence à répétition. Ces effets s’ajoutent également à l’apparition de sauts de cycle dans les mesures de phase. Des techniques spécifiques sont implémentées dans certains algorithmes de positionnement par satellites afin de détecter et corriger les sauts de cycle mais leurs performances sont très limitées en cas de scintillations ionosphériques. Lorsqu’un saut de cycle se produit et qu’il est détecté, l’ambiguïté entière initiale de la fréquence et du satellite concerné doit être réinitialisée. Si des sauts de cycles se produisent de manière trop fréquente et sur les signaux de plusieurs satellites simultanément, cela pousse les algorithmes de positionnement basés sur un filtre de type Kalman à repasser par une période de convergence avant de retrouver des performances optimales. Les sauts de cycle non-détectés introduiront un biais dans les mesures de phase concernées et éventuellement dans la solution estimée. En cas de scintillations ionosphériques, les mesures brutes GNSS de code et de phase sont également de moindre précision, ce qui rend potentiellement un modèle stochastique standard complètement irréaliste avec des conséquences désastreuses pour la validité de la solution finale et le bon fonctionnement du contrôle d’intégrité (Hartmann et Leitinger, 1984 ; Wanninger, 1993 ; Aquino et al., 2007). En conséquence, les performances des algorithmes GNSS en termes d’exactitude, de continuité et de fiabilité peuvent être fortement dégradées. La Figure 4 illustre une comparaison entre les performances de l’algorithme PPP dans des conditions de scintillations ionosphériques actives et calmes à la station d’Inconfidentes, au Brésil (Lonchay, 2019).

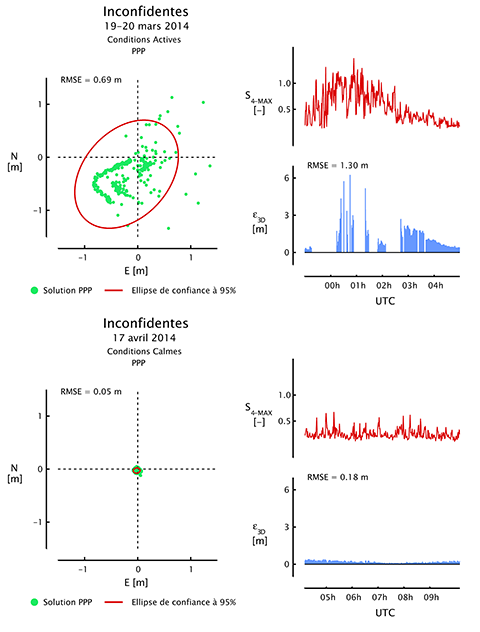
Figure 4. Performances du positionnement horizontal et tridimensionnel de l'algorithme PPP dans des conditions de scintillation ionosphérique active (haut) et au repos (bas) à la station d'Inconfidentes, Brésil

19Les scintillations ionosphériques constituant une menace majeure pour le positionnement par satellites en raison des effets susmentionnés, de nombreuses études ont été menées dans le but de surveiller, modéliser et cartographier les scintillations ionosphériques polaires et équatoriales ainsi que de mettre au point des techniques d’atténuation de leurs effets dévastateurs.

20Une première catégorie de techniques d’atténuation cible les algorithmes mis en œuvre dans le processeur de signal numérique des récepteurs GNSS. Des résultats prometteurs ont été obtenus en développant un algorithme pour boucle à verrouillage de phase (PLL) adaptatif, basé sur un filtre de Kalman qui s’adapte aux conditions rencontrées (Susi et al., 2014a ; Susi et al., 2014b ; Susi et al., 2017). Une autre approche consiste à remplacer la boucle à verrouillage de phase (PLL) par une boucle à verrouillage de fréquence (FLL - Frequency Lock Loop), réputée plus robuste en cas d’atténuation de l’amplitude du signal. Cependant, les applications GNSS exigeant de hautes performances nécessitent des mesures de phase qu’une boucle à verrouillage de fréquence (FLL) ne peut effectuer. Une technique efficace consiste alors à utiliser un circuit PLL assistée par un circuit FLL pour contrôler conjointement l’oscillateur à contrôle numérique de porteuse (Lin Tao et al., 2014).

21Une autre tendance dans la recherche sur les scintillations ionosphériques consiste à développer des modèles de propagation dans le but de surveiller et de prévoir l’ampleur de leurs effets sur les signaux GNSS. La production de cartes est étroitement liée à l’existence de modèles de scintillations ionosphériques. Ces modèles peuvent alors être combinés à des techniques d’interpolation spatiale appliquées à des mesures effectives de scintillations ionosphériques afin de prédire le niveau de scintillation dans une région spécifique de la Terre (Hamel et al. 2014). Avec le développement de réseaux spécifiques de surveillance des scintillations ionosphériques, des techniques d’interpolation spatiale, telles que le Krigeage, ont également été utilisées afin d’établir des cartes de prévision des effets des scintillations ionosphériques sur les signaux GNSS (Kieft et al., 2014). Les variables d’intérêt peuvent être directement des indices de scintillation, tels que l’indice S₄, ou d’autres variables dérivées, comme la variance des mesures effectuées par les boucles à verrouillage du tracker de récepteurs de type ISMR (Sreeja et al., 2011) qui peuvent être estimées à l’aide du modèle de Conker (Conker et al., 2003). Le but ultime de la cartographie des effets des scintillations ionosphériques sur les signaux GNSS est de fournir aux utilisateurs opérant dans des zones géographiques sensibles des informations supplémentaires concernant le niveau de scintillation ionosphérique.

22Une approche efficace pour atténuer l’impact des scintillations ionosphériques sur le positionnement par satellites repose sur la modélisation stochastique des observations en fonction des effets de scintillation ionosphérique rencontrés. Cette approche a donné de bons résultats pour le positionnement RTK aux latitudes équatoriales grâce à une augmentation significative du taux de réussite des processus de résolution des ambiguïtés. Elle est basée sur le fait que les observations brutes affectées par des scintillations ionosphériques sont caractérisées par un niveau de bruit de mesure plus élevé et la présence de biais. Cette modélisation stochastique utilise des paramètres fournis par le tracker de récepteurs de type ISMR qui, grâce à des modèles spécifiques, permettent de calculer la valeur des variances des mesures concernées et ainsi obtenir un modèle stochastique plus réaliste en cas de scintillations ionosphériques (Aquino et al., 2009 ; Park et al., 2017 ; da Silva et al., 2010 ; Warnant et al., 2009).

23Les performances de l’algorithme PPP sont très sensibles aux scintillations ionosphériques car elles dépendent de la haute précision des mesures de phase qui, comme mentionné précédemment, peuvent être affectées de sauts de cycle en cas de scintillations ionosphériques. Une technique intéressante pour améliorer les performances de l’algorithme PPP en cas de scintillations ionosphériques provoquant de nombreux et fréquents sauts de cycle consiste à étendre la phase de prétraitement des mesures GNSS en effectuant des tests de détections de saut de cycle sur plusieurs types de combinaisons impliquant des mesures de code et de phase associées à plusieurs fréquences. Les observations liées à des fréquences sur lesquelles des sauts de cycle sont ainsi détectés sont tout simplement exclues du processus d’estimation des paramètres inconnus, pour autant que la redondance et la qualité de la géométrie satellitaire restent acceptables (Zhang et al., 2014).

24Ainsi donc, l’objectif de cette recherche est d’élaborer des stratégies afin de renforcer la robustesse du positionnement par satellites en cas de scintillations ionosphériques équatoriales. Comme nous allons le montrer dans la suite de cet article, la robustesse des algorithmes GNSS est quantifiée par leurs performances de positionnement en termes d’exactitude, de continuité et de fiabilité. Ces critères de performances sont définis dans le cadre de cette recherche de la manière suivante. L’exactitude de la solution fournie par un algorithme GNSS est l’erreur entre la solution calculée et la vraie solution utilisée comme référence. Dans notre étude, les stations ISMR utilisées sont fixes et leurs positions de référence ont été calculées grâce à un logiciel de positionnement GNSS en utilisant de longues séries de données durant des conditions calmes. L’exactitude d’un algorithme GNSS peut donc être mesurée grâce au paramètre RMSE (Root Mean Square Error). La continuité d’un algorithme mesure sa capacité à fournir une solution à tout instant. Il s’agit de son taux de succès noté SR (Success Rate) dans le cadre de cette étude. La continuité d’un algorithme GNSS est mesurée comme la proportion d’époques observationnelles pour lesquelles une solution valide existe. Enfin, la fiabilité d’un algorithme GNSS est mesurée comme la proportion d’époques observationnelles pour laquelle l’algorithme est capable de fournir une solution qui correspond à son exactitude standard. Pour les algorithmes SPP et PPP, les paramètres SR₁₀ et SR_0.5 mesure la proportion du temps pendant laquelle les algorithmes parviennent à fournir une solution avec une exactitude meilleure que 10 m et 0.5 m, respectivement.

25Les stratégies visant à limiter les effets des scintillations ionosphériques pour le positionnement par satellites développées dans le cadre de cette recherche combinent et étendent des pistes décrites dans la brève revue de la littérature évoquée ci-dessus. Elles sont construites sur les caractéristiques spatiotemporelles des scintillations ionosphériques équatoriales mise en évidence par des méthodes d’analyse spatiale et géostatistiques spécifiques appliquées aux mesures GNSS et ISMR (cfr section IV). Les informations spatiotemporelles collectées sont contenues dans des skymaps de scintillations ionosphériques qui sont exploitées par les algorithmes SPP et PPP afin de renforcer leurs modèles stochastiques respectifs (cfr section V). Ce dernier élément constitue l’originalité majeure de cette recherche.

IV. Approche géostatistique

A. Conditions expérimentales

26Cette recherche est entièrement basée sur des mesures GNSS et ISMR recueillies durant le dernier maximum solaire (cycle solaire 24) au travers d’un réseau de neuf stations ISMR situées près de l’équateur magnétique au Brésil. La zone géographique ciblée est directement sous la menace de scintillations ionosphériques résultant d’irrégularités ionosphériques associées à l’anomalie ionosphérique équatoriale (EIA). Les techniques d’analyse spatiale exploitées dans le cadre de cette section s’appliquent à des skyplots représentant les positions des satellites dans le ciel de l’utilisateur exprimées en coordonnées horizontales. Les skyplots constituent un cas particulier de projection cartographique de Postel. Il s’agit d’une projection équidistante azimutale en aspect polaire appliquée à un demi-hémisphère unitaire centré sur la position de l’utilisateur et sur lequel évoluent fictivement les satellites GNSS. Chaque satellite visible par l’utilisateur constitue un individu d’un échantillon spatial reporté dans ce canevas grâce à sa composante géométrique, c’est-à-dire sa position dans le ciel de l’utilisateur exprimée en coordonnées d’azimut et d’élévation. La composante attributaire de l’échantillon spatial est composée des valeurs de l’indice de scintillation ionosphérique S₄ décrit précédemment dans cet article associées aux différents satellites observés. Étant donné que les satellites gravitent en permanence autour de la Terre et que les conditions ionosphériques évoluent avec le temps, les composantes géométriques et attributaire de l’échantillon spatial constitués sont également variables dans le temps. Comme nous l’avons décrit précédemment, l’indice S₄ est calculé sur une période de 60 s. En conséquence, notre analyse spatiale et la production de skymaps est également basée sur un échantillonnage à 60 s.

27Afin de densifier l’échantillon spatial expérimental avec des mesures supplémentaires, nous avons décidé d’utiliser la station d’Inconfidentes comme référence en raison de sa position centrale dans le réseau ISMR. Ensuite, nous avons projeté tous les points de percée ionosphériques (IPP - Ionospheric Pierce Points) associés à toutes les stations du réseau expérimental dans le ciel de l’utilisateur situé à Inconfidentes, comme décrit par la Figure 5. Les points de percée ionosphériques sont constitués par les intersections des lignes de visée joignant chaque station ISMR à chaque satellite GNSS observable avec une coquille d’épaisseur infinitésimale située à 350 km d’altitude et qui représente l’ionosphère. L’altitude de 350 km est déterminée en fonction du profil de densité en électrons libres de l’ionosphère et de la localisation en altitude des irrégularités ionosphériques causant des scintillations ionosphériques sur les signaux GNSS. Les skyplots expérimentaux utilisés dans le cadre de cette analyse incluent l’ensemble des IPPs du réseau expérimental ISMR projetés dans le ciel d’un utilisateur situé à Inconfidentes et chaque IPP est porteur d’une valeur de l’indice de S₄ qui constitue notre variable d’intérêt. Nous désignons ces skyplots par le terme de skyplots ionosphériques et nous différencions les skyplots des skymaps selon l’aspect ponctuel ou continu de ceux-ci, respectivement. Dans le cadre de cette recherche, nous mesurons les distances entre les individus d’un échantillon spatial comme des distances angulaires.

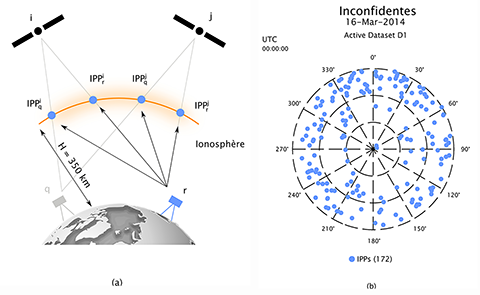
Figure 5. Dans un réseau de stations ISMR, tous les points de percée ionosphériques (IPPs) associés à toutes les paires récepteur-satellite peuvent être projetées dans le ciel d’un utilisateur situé à une position donnée à l’intérieur du réseau expérimental. Dans le cadre de cette recherche, nous avons choisi la position de la station d’Inconfidentes comme position de référence. Cette technique est utilisée afin de densifier l’échantillon spatial en ajoutant des points de mesure supplémentaires.

B. Autocorrélation spatiale

28L’analyse de l’autocorrélation spatiale dans les skyplots de scintillations ionosphériques est effectuée selon trois niveaux. Le premier niveau vise à détecter la présence d’autocorrélation spatiale globale en considérant tous les individus des échantillons spatiaux. Le deuxième niveau porte sur la détermination de l’échelle spatiale caractéristique de cette autocorrélation. En d’autres termes, l’objectif de ce niveau d’analyse est de déterminer les dimensions de la zone d’influence qui caractérise la dépendance spatiale de l’attribut pris en considération, c’est-à-dire l’indice de scintillation ionosphérique S₄. Il s’agit d’une étape d’importance primordiale pour la paramétrisation de l’interpolation spatiale et pour le prototypage des stratégies d’atténuation des effets des scintillations ionosphériques sur les algorithmes de positionnement par satellites. Le troisième niveau mesure la présence d’autocorrélation spatiale locale et vise à détecter et localiser les structures spatiales qui influencent l’autocorrélation spatiale globale.

29Afin de détecter la présence d’une autocorrélation spatiale globale dans les skyplots expérimentaux, nous analysons l’évolution de trois indices d’autocorrélation spatiale globale pendant une période de sept jours consécutifs (Figure 6). Nous utilisons en particulier l’indice I de Moran, l’indice C de Geary et la statistique General G de Getis-Ord (Lentz, 2009). Comme expliqué précédemment, l’état de l’ionosphère évolue au cours du temps et les satellites GNSS se déplacent continuellement selon leurs orbites respectives. En conséquence, il est attendu que l’autocorrélation spatiale globale évolue également au cours du temps en fonction des changements apparaissant à la fois dans la composante géométrique et attributaire de la variable d’intérêt : l’indice de scintillation ionosphérique S₄. Les trois indices d’autocorrélation spatiale évoluent différemment et doivent être interprétés spécifiquement.

30Une valeur positive (resp. négative) de l’indice I de Moran traduit une autocorrélation positive (resp. négative). Plus l’indice I de Moran est élevé en valeur absolue (proche du I maximum, +1, ou du I minimum, -1), plus l’autocorrélation spatiale globale, positive ou négative, est forte.

31L’indice C de Geary peut théoriquement varier entre 0 et 2. La valeur de 1 traduit l’absence d’autocorrélation spatiale significative et les valeurs de 0 et 2 traduisent respectivement des autocorrélations négatives et positives fortement significatives. Cet indice évolue de manière opposée à celle du I de Moran. En outre, il est également plus sensible à la présence d’une autocorrélation spatiale locale et à la présence de points froids et de points chauds dans la distribution spatiale de l’indice S₄. Les points froids et les points chauds peuvent être définis comme l’agrégation spatiale d’entités caractérisées par une faible ou une haute valeur de l’indice S₄, respectivement.

32La statistique General G de Getis-Ord est analysée par le biais de son score standard (Z-Score). Par définition, ce score standard varie sur une échelle continue non-bornée. Les valeurs positives et négatives du score standard correspondent à une autocorrélation spatiale positive ou négative, respectivement. Le caractère significatif du score standard est déterminé en comparant la valeur calculée à une table de la Loi Normale. Ceci explique que l’intervalle de confiance de la Figure 6 pour cette statistique est une droite parallèle à l’axe du temps. La statistique General G de Getis-Ord varie conformément à l’indice I de Moran.

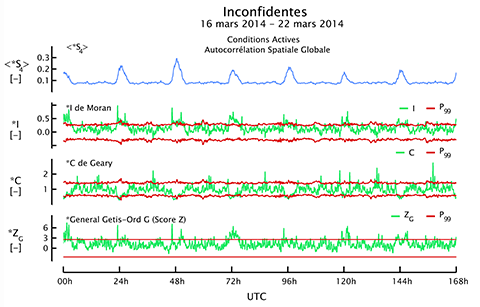
Figure 6. Mesure de l'autocorrélation spatiale globale dans les skyplots de scintillations ionosphériques pendant une période de sept jours consécutifs, caractérisée par des conditions actives à la station ISMR d'Inconfidentes, au Brésil. L’autocorrélation spatiale globale est mesurée à l’aide de l’indice I de Moran, de l’indice C de Geary et de la statistique General G de Getis-Ord. La variable cible est l'indice de scintillation ionosphérique S₄. L’autocorrélation spatiale globale est significativement positive (intervalle de confiance à 99 % représenté par les courbes rouges) pendant les heures qui suivent le coucher de soleil local, c’est-à-dire lors de l’apparition de scintillations ionosphériques, comme l’indique l’évolution de l’indice S₄ moyen.

33La Figure 6 révèle que l’autocorrélation spatiale globale est détectée comme étant significativement positive (99 %) pendant les heures qui suivent le coucher de soleil local, c’est-à-dire lors de l’apparition d’irrégularités ionosphériques liées au mécanisme de l’EIA dans cette région de la Terre. La présence d’autocorrélation spatiale globale significative constitue une condition nécessaire pour l’application de techniques d’interpolation spatiale en vue d’établir une cartographie des scintillations ionosphériques à un instant donné. Les trois indices d’autocorrélation spatiale ne fournissent pas toujours des résultats similaires, ce qui prouve leur complémentarité.

34Sur base de ces résultats, quatre études de cas ont été menées afin de poursuivre l’analyse de l’autocorrélation spatiale dans les skyplots de scintillations ionosphériques aux niveaux ultérieurs. Le premier cas, noté CS1, a été sélectionné en raison de la valeur élevée de l’indice I de Moran. Le deuxième cas, noté CS2, a été choisi en raison de la valeur élevée de l’indice C de Geary. Le troisième cas, noté CS3, a été analysé en raison de la valeur élevée du score standard de la statistique General G de Getis-Ord. Le quatrième cas, noté CS4, a été étudié en raison de l’absence d’autocorrélation spatiale globale significative selon les trois indices susmentionnés. La Figure 7 présente les skyplots de scintillations ionosphériques associés aux 4 cas sélectionnés. Chacun de ces skyplots correspond donc à un instant donné.

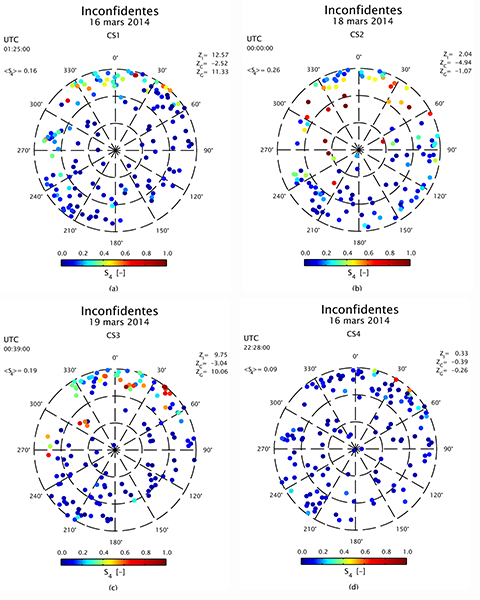
Figure 7. Skyplots de scintillations ionosphériques représentant les valeurs de l’indice S₄ de quatre échantillons spatiaux associés à quatre cas instantanés.

35Le second niveau d’analyse de l’autocorrélation spatiale consiste à mesurer l’autocorrélation spatiale selon une série de distances critiques afin d’en déterminer l’échelle spatiale. Cependant, cette opération nécessite de modifier légèrement la méthode utilisée pour calculer l’autocorrélation spatiale. En effet, plutôt que d’intégrer l’ensemble des individus dans le calcul d’autocorrélation spatiale selon un système de pondération basé sur les interdistances entre individus, nous appliquons une sélection de ces individus selon une échelle de distance discrétisée en plusieurs classes. Pour chaque classe de distance, seuls les couples de points caractérisés par une interdistance inclue dans la classe de distance considérée sont pris en compte pour calculer un indice d’autocorrélation spatiale. Un autocorrélogramme est établi pour les différents indices d’autocorrélation spatiale en reportant les valeurs de ces indices associées à chaque classe de distance considérée.

36L’interprétation des autocorrélogrammes spatiaux est complexe en raison des nombreux facteurs pouvant influencer le calcul des indices pour les différentes classes de distance. Cependant, dans notre application, il peut être facilité par une observation attentive de la Figure 7. Celle-ci fournit en effet des indices précieux, tels que le fait que les skyplots de scintillations ionosphériques montrent plusieurs types de configuration. En particulier, les cas CS1 et CS3 présentent des similitudes évidentes qui se répercutent dans les autocorrélogrammes spatiaux de la Figure 8.

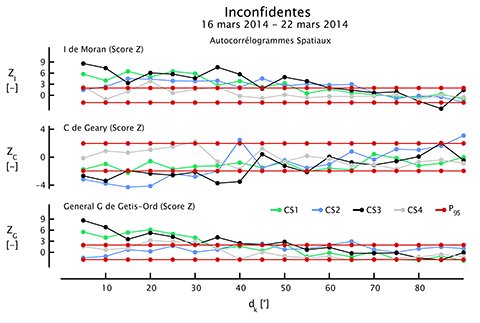
Figure 8. Autocorrélogrammes spatiaux de l’indice I de Moran, de l’indice C de Geary et de la statistique General G de Getis-Ord, pour les cas d’étude CS1, CS2, CS3 et CS4. Les valeurs des indices d'autocorrélation spatiale entrent à l'intérieur de leurs intervalles de confiance respectifs à une distance angulaire maximale d'environ 40°. L'autocorrélation spatiale maximale est observée dans l’intervalle des distances entre 15° et 20°.

37Ces deux cas sont similaires en ce qui concerne l’indice I de Moran et la statistique General G de Getis-Ord, qui ciblent principalement l’autocorrélation spatiale globale. En revanche, ils diffèrent par la valeur de l’indice C de Geary qui leur est associée. Ce dernier indice est plus sensible à l’autocorrélation spatiale locale et à la présence de points chauds. Par conséquent, le cas CS3 est plus susceptible de présenter une autocorrélation spatiale locale et des points chauds plus marqués que le cas CS1. Les autocorrélogrammes spatiaux sont particulièrement utiles pour estimer l’échelle caractéristique de l’autocorrélation spatiale. À cet égard, les autocorrélogrammes spatiaux illustrés par la Figure 8 montrent que les indices d’autocorrélation spatiale entrent généralement à l’intérieur de leurs intervalles de confiance respectifs à une distance angulaire maximale de 40°. De plus, l’autocorrélation spatiale maximale est observée dans l’intervalle de distances entre 15° et 20°.

38Le troisième niveau d’analyse de l’autocorrélation spatiale tente de détecter et de localiser des structures spatiales locales significatives. À cet effet, nous utilisons la variante locale de la statistique General G de Getis-Ord. L’indice d’autocorrélation spatiale local de Getis-Ord est noté Gi* et peut être calculé selon les équations 4 et 5. D’après ces équations, on peut remarquer que l’indice Gi* peut être calculé en tout point d’un skyplot de scintillations ionosphériques et pas seulement aux positions des individus. Ceci présente un avantage significatif puisque que cela permet déjà de générer un produit spatial continu, à savoir une skymap de l’indice Gi*. Dans les équations 4 et 5, z est la variable d’intérêt, c’est-à-dire l’indice de scintillation ionosphérique S₄, et w est une fonction de pondération basée sur la distance. L’indice Gi* est calculé dans une fenêtre de convolution de rayon d_k qui a été fixée à 20° sur base de l’analyse des autocorrélogrammes spatiaux. La distribution théorique de l’indice Gi* n’est pas toujours fiable et difficilement vérifiable pour les cas particuliers que nous envisageons dans le cadre de cette étude. En conséquence, nous lui avons préféré une simulation de Monte Carlo qui permet de calculer les paramètres de la distribution de l’indice Gi* et, par extension, de détermine son score standard. Chaque pixel d’une skymap de l’indice Gi* est donc porteur de la valeur du score standard de l’indice Gi* au point considéré. Dans la suite de cet article, ce type de skymap est désigné sous le terme GOS (Getis-Ord Score). La Figure 9 illustre les skymaps de type GOS obtenues pour chaque cas d’étude susmentionné. Sur ces skymaps, seuls les pixels porteurs d’une valeur significative (95 %) du score standard de l’indice Gi* sont représentés. Les pixels porteur d’un score significativement positif doivent être interprétés comme des pixels faisant partie d’un agrégat de hautes valeurs de l’indice S₄, c’est-à-dire un point chaud. Les pixels porteurs d’un score significativement négatif correspondent à des agrégats de faibles valeurs de l’indice S₄, soit des points froids (ESRI). Les skymaps de type GOS constituent le principal produit spatial exploité dans le cadre de cet article (section V) pour prototyper les stratégies d’atténuation des effets des scintillations ionosphériques pour les algorithmes de positionnement par satellites SPP et PPP.

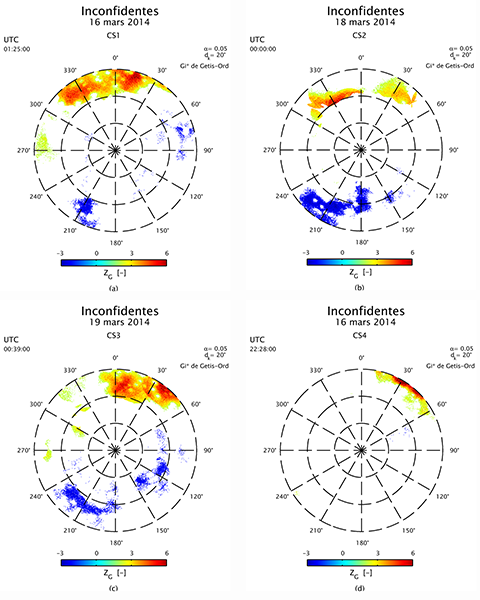
Figure 9. Skymaps de type GOS représentant les scores standards significatifs (95 %) de l’indice d’autocorrélation spatiale locale de Getis-Ord, noté Gi* pour les études de cas CS1, CS2, CS3 et CS4.

V. Prototypage de stratégies d’atténuation des effets des scintillations ionosphériques sur le positionnement par satellites SPP et PPP

39Dans cette dernière section, nous démontrons comment les informations spatiotemporelles sur les scintillations ionosphériques équatoriales modélisées par les skyplots et les skymaps peuvent être exploitées dans des stratégies d’atténuation de leurs effets qui visent à améliorer les performances des algorithmes de positionnement par satellites SPP et PPP. À cette fin, nous avons sélectionné plusieurs épisodes de scintillations ionosphériques d’environ 6 heures chacun, au cours desquels des dégradations sévères des performances de ces algorithmes ont été observées à la station d’Inconfidentes, au Brésil. Ces prototypes ont été intégrés dans le logiciel de positionnement GNSS RTKLIB (Takasu, 2016). Dans le cadre de cette recherche, le logiciel RTKLIB est considéré comme l’externalisation du processeur de navigation d’un récepteur GNSS.

40Les stratégies décrites dans cette section sont caractérisées par la création de masques spatiaux spécifiques basés sur des skymaps de type GOS représentant les conditions de scintillation ionosphérique dans le ciel de l’utilisateur à un instant donné. Les indices de scintillation ionosphérique S₄ étant calculés toutes les 60 s, une skymap de type GOS est construite également toutes les 60 s et intégrée par les algorithmes SPP et PPP. Dans le cadre de cette recherche, une position est également calculée toutes les 60 s avec le logiciel RTKLIB pour les algorithmes SPP et PPP.

41L’application de masques spatiaux peut être considérée comme une modification extrême du schéma de pondération des algorithmes GNSS, car l’exclusion de mesures par ces masques correspond à la définition d’un poids nul dans le processus d’estimation des paramètres des algorithmes SPP et PPP.

A. Développement des stratégies

42La première catégorie de stratégies (SM01) développée dans cette recherche concerne l’application de masques spatiaux visant à rejeter certains satellites du processus d’estimation des paramètres inconnus des algorithmes SPP et PPP. L’application d’un masque horizontal omnidirectionnel basé sur l’élévation est très courante en positionnement par satellites car les mesures effectuées sur les signaux émis par des satellites de faible élévation sont plus susceptibles d’être affectées par des effets de multitrajet, des sauts de cycle et un niveau de bruit de mesure plus élevé en raison de la propagation à travers des couches plus denses de l’atmosphère.

43Les versions originales des algorithmes SPP et PPP considérés dans le cadre de cette recherche utilisent un masque d’élévation de 5° dans toutes les directions (Original). Néanmoins, il est fréquent d’augmenter cette valeur à 15° pour des applications de positionnement et de navigation de plus haute précision. Cette modification mineure est à la base de la première stratégie testée dans le cadre de cet article (SM01a) et dont les performances sur épisode expérimentales sont illustrées par la Figure 10. Un masque d’élévation plus important réduira encore plus le risque d’inclure des mesures corrompues dans le processus d’estimation des paramètres des algorithmes SPP et PPP, mais il augmentera également la dilution de la précision (DOP - Dilution of Precision) en dégradant la qualité de la géométrie satellitaire. Les scintillations ionosphériques affectant fréquemment les satellites proches de l’horizon, la stratégie SM01a devrait améliorer les performances des algorithmes SPP et PPP en cas de scintillations. Cependant, cette stratégie rejette également parfois les signaux de certains satellites qui ne sont pas affectés par des scintillations ionosphériques. Ainsi, le processus de masquage n’est pas adaptatif aux conditions de scintillations ionosphériques rencontrées.

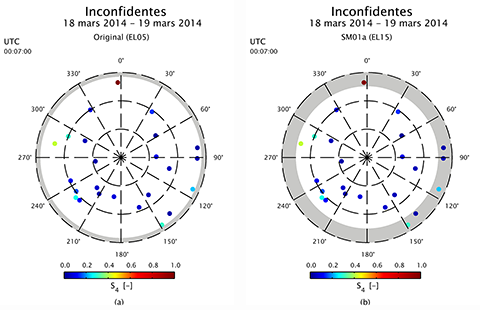
Figure 10. Masque d’élévation original fixé à 5° (Original, a) et masque d’élévation fixé à 15° dans la stratégie SM01a (b). L’application de masques en positionnement par satellites consiste à rejeter certains satellites d’un algorithme GNSS en fonction de leur position dans le ciel de l’utilisateur.

44Afin d’adapter le masque spatial aux conditions de scintillations ionosphériques rencontrées, nous avons conçu un masque horizontal basé sur les skymaps de type GOS (SM01b). Son objectif est de permettre la détection des directions dans le ciel de l’utilisateur qui sont caractérisées par la manifestation d’effets de scintillations ionosphériques. Cette stratégie devrait produire des résultats probants pour les scintillations ionosphériques équatoriales, car les irrégularités ionosphériques à leur origine sont associées à l’EIA dont la position est géographiquement contrainte. En d’autres mots, pour une localisation donnée dans la zone intertropicale, il est fréquent d’observer des phénomènes de scintillations ionosphériques sur des signaux GNSS dans certaines directions particulières. Dans la stratégie SM01b, les directions azimutales depuis le centre d’un skyplot sont traitées successivement avec un pas angulaire de 1°. Pour chaque direction considérée, un masque d’élévation est établi à une valeur qui correspond à l’élévation du pixel significativement positif le plus élevé. Néanmoins, la valeur minimale du masque d’élévation reste fixée à 5° lorsqu’aucun pixel porteur d’un score standard de l’indice Gi* significatif n’est détecté dans la direction considérée, comme l’illustre la Figure 11.

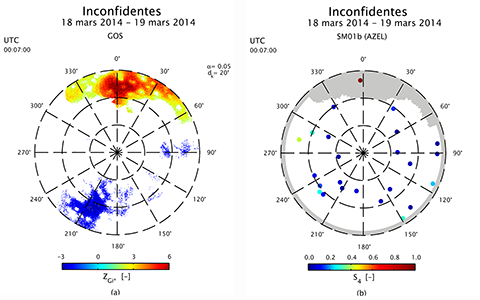
Figure 11. Skymap ou cartographie du GOS (a). Stratégie de masquage SM01a sur le skyplot correspondant (b). Cette stratégie consiste à appliquer un masque éliminant des observations GNSS brutes, pour les estimations des paramètres des algorithmes SPP et PPP, les signaux émis par les satellites dont la hauteur angulaire au-dessus de l’horizon est inférieure à 5° si aucun pixel chaud et statistiquement significatif n’est trouvé dans la direction courante sur la skymap. Si des pixels chauds et significatifs existent dans la direction courante sur cette skymap, c’est la hauteur angulaire du pixel le plus chaud et statistiquement significatif qui est choisie pour le masquage.

45La Figure 12 et le Tableau 1 présentent les résultats de performances des stratégies SM01a et SM01b pour les algorithmes SPP et PPP pour un épisode expérimental donné de 6 h caractérisé par des effets de scintillations ionosphériques intenses à la station de Inconfidentes au Brésil. L’amélioration la plus significative concerne l’exactitude de l’algorithme PPP pour la stratégie SM01b avec un paramètre RMSE qui passe de 2.85 m à 1.06 m (-62.83 %) par rapport à la version originale de l’algorithme. La stratégie SM01b offre des performances supérieures à la stratégie SM01a, basée sur un masque uniforme dans toutes les directions, dont le paramètre RMSE (2.82 m) est comparable à la version originale de l’algorithme. Cela signifie qu’un masque spatial directionnel adaptif est plus approprié pour atténuer les effets des scintillations ionosphériques qu’un masque d’élévation isotrope. Pour l’algorithme SPP, l’utilisation de la stratégie SM01b entraîne également une diminution de la valeur du paramètre RMSE de 9.48 m à 8.74 m (-7,87 %). Cependant, ses performances en termes de continuité sont inférieures (taux de succès mesurés à 99.80 % et 64.27 % pour les algorithmes SPP et PPP, respectivement) à la stratégie SM01a (taux de succès mesurés à 100.00 % et 66.67 % pour les algorithmes SPP et PPP, respectivement). Cela signifie que le masque d’élévation directionnel est parfois encore trop permissif par rapport au masque d’élévation isotrope et qu’il pourrait ne pas rejeter certaines mesures corrompues, qui ne sont pas nécessairement toujours dues aux scintillations ionosphériques. C’est la raison pour laquelle nous proposons ci-dessous de nouvelles stratégies.

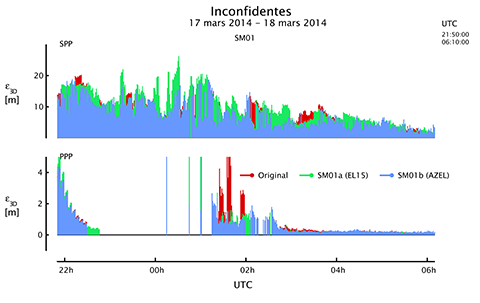
Figure 12. Performances des stratégies SM01a (EL15) et SM01b (AZEL) pour les algorithmes SPP (haut) et PPP (bas) évaluées à l’aide du logiciel RTKLIB durant un épisode expérimental marqué par des scintillations ionosphériques sévères à la station ISMR de Inconfidentes au Brésil.

Stratégie	SPP			PPP
	RMSE	SR	SR10	RMSE	SR	SR0.5
Original	9.48 m	98.00%	65.67%	2.85 m	57.88%	41.72%
SM01a (EL15)	10.65 m	100.00%	78.24%	2.82 m	66.67%	39.52%
SM01b (AZEL)	8.74 m	99.80%	80.04%	1.06 m	64.27%	39.52%

Tableau 1. Performances des stratégies SM01a (EL15) et SM01b (AZEL) pour les algorithmes SPP et PPP évaluées à l’aide du logiciel RTKLIB durant un épisode expérimental marqué par des scintillations ionosphériques sévères à la station ISMR de Inconfidentes au Brésil. L’exactitude des stratégies est mesurée par le biais du paramètre RMSE (Root Mean Square Error), la continuité des algorithmes est mesurée par le taux de réussite des algorithmes à fournir une solution valide (SR – Success Rate) et la fiabilité des algorithmes SPP et PPP est mesurée à l’aide des paramètres SR₁₀ et SR_0.5, respectivement, qui déterminent le taux de succès des deux algorithmes à fournir une solution avec une exactitude meilleure que 10 m et 0.5 m, respectivement.

46La deuxième catégorie de stratégies prototypées dans le cadre de cette recherche est basée sur la construction de masques spécifiquement calculés en exploitant des skymaps de type GOS. Ces masques spatiaux sont établis en fonction des pixels porteurs de valeurs significativement positives du score standard de l’indice Gi*. Étant donné que ces pixels traduisent la présence d’agrégats de valeurs élevées de l’indice S₄, ces pixels déterminent les zones du skyplot qui doivent être masquées (SM02a). Contrairement à la catégorie précédente (SM01), cette deuxième catégorie de stratégies (SM02) repose sur une prédiction statistique reposant sur de solides principes théoriques, comme l’illustre la Figure 13.

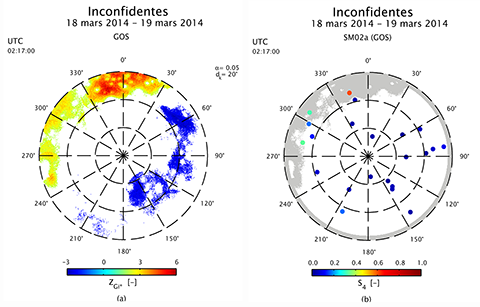
Figure 13. La stratégie SM02a consiste à calculer un masque d’élévation basé sur les skymaps de type GOS. Ces skymaps sont caractérisées par des pixels qui sont porteurs des valeurs significatives du score standard de l’indice de Getis-Ord Gi*. Les pixels significativement positifs (95%) correspondent à des zones d’agrégats de hautes valeurs de l’indice S₄ (points chauds).

47L’analyse de skymaps de type GOS associées à des époques observationnelles successives séparées de 60 s a permis de mettre en évidence la forte variabilité spatiotemporelle des scintillations ionosphériques se manifestant dans la région intertropicale. Par conséquent, l’application stricte d’un masque spatial calculé toutes les 60 s, en raison de la contrainte posée par le calcul de l’indice S₄, ne peut prendre en compte cette grande variabilité spatiotemporelle. Dans le cas d’un algorithme GNSS tel que l’algorithme PPP caractérisé par un processus d’estimation de paramètres basé sur un filtre de Kalman, la forte variabilité spatiotemporelle des masques spatiaux entraîne des discontinuités graves dans les observations GNSS injectées dans le filtre. Cela ne constitue pas de bonnes conditions en vue d’atteindre des performances de positionnement et de navigation optimales. Pour cette raison, nous avons développé deux stratégies supplémentaires en exploitant d’abord un tampon spatial (SM02b), puis un tampon spatiotemporel (SM02c). Le tampon spatial consiste simplement à dilater le masque spatial original, élaboré par la stratégie SM02a, d’une distance angulaire de 5°. Le tampon spatiotemporel consiste également à rejeter les satellites qui ne sont pas visibles de manière continue pendant une période de minimum 10 min. La Figure 14 illustre l’application du masque spatiotemporel pour un épisode expérimental donné durant lequel de sévères scintillations ionosphériques sont rencontrées à la station ISMR de Inconfidentes au Brésil.

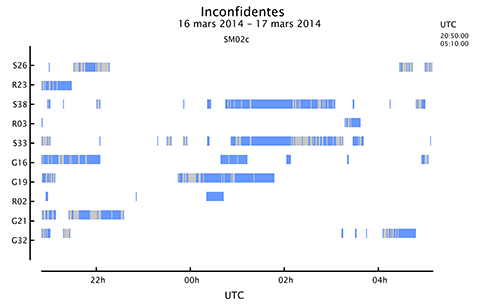Figure 14. La stratégie SM02c consiste à calculer un masque spatiotemporel basé sur les skymaps de type GOS. Cette stratégie implémente un tampon spatial de 5° autour du masque produit par la stratégie SM02a et un tampon temporel de 10 minutes. Ce dernier a pour objectif de rejeter tous les satellites qui ne sont pas visibles pendant un minimum de 10 min, évitant ainsi de multiples discontinuités dans les mesures brutes exploitées par les algorithmes SPP et PPP.

48La Figure 15 et le Tableau 2 décrivent les performances de la catégorie de stratégies SM02 pour les algorithmes SPP et PPP au cours d’un épisode expérimental durant lequel de sévères scintillations ionosphériques ont été observées à la station d’Inconfidentes. Les avancées les plus impressionnantes de cette catégorie de stratégies concernent l’algorithme PPP avec une augmentation significative de l’exactitude et de la fiabilité. La stratégie SM02a diminue déjà le paramètre RMSE de l’algorithme PPP de 1.65 m à 0.45 m (-72,93 %). Elle augmente également la continuité de la solution de l’algorithme PPP de 83.63 % à 96.61 % (+ 15,51 %). Cependant, cette stratégie ne parvient pas à gérer les perturbations les plus sévères qui se produisent autour de 03h00 UTC. La stratégie SM02b (tampon spatial de 5°) et la stratégie SM02c (tampon spatial de 5° et tampon temporel de 10 minutes) apportent une amélioration radicale des performances de l’algorithme PPP au cours de cet épisode expérimental. Ils permettent de résoudre les perturbations sévères observées vers 03h00 UTC. Les stratégies SM02b et SM02c réduisent respectivement le paramètre RMSE de l’algorithme PPP à 0.40 m (-76.10%, par rapport à la version originale de l’algorithme) et 0.46 m (-72.18 % par rapport à la version originale de l’algorithme), respectivement. En termes d’exactitude, la stratégie SM02c est légèrement moins performante que la stratégie SM02b. En revanche, l’atout de la stratégie SM02c est le taux de réussite de l’algorithme PPP, qui passe de 83.63 % à 100.00 %, ce qui constitue une amélioration significative de la continuité de la solution de navigation calculée (+ 19,57 %).

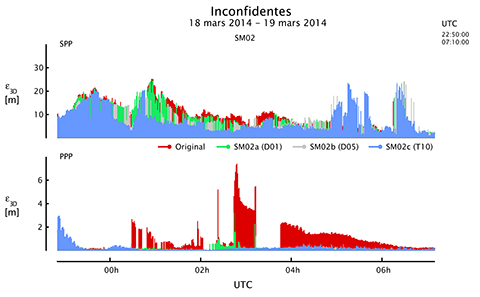
Figure 15. Performances des stratégies SM02a, SM02b et SM02c pour les algorithmes SPP (haut) et PPP (bas) évaluées à l’aide du logiciel RTKLIB durant un épisode expérimental marqué par des scintillations ionosphériques sévères à la station ISMR de Inconfidentes au Brésil. La stratégie SM02a est basée sur un masque spatial calculé à partir des skymaps de type GOS. Les stratégies SM02b et SM02c implémentent respectivement un tampon spatial de 5° et un tampon spatial 5° ajouté à un tampon temporel de 10 minutes.

Stratégie	SPP			PPP
	RMSE	SR	SR10	RMSE	SR	SR0.5
Original	11.51 m	91.62 %	49.90 %	1.66 m	83.63 %	30.94 %
SM02a (D01)	10.95 m	94.81 %	62.87 %	0.45 m	96.61 %	88.02 %
SM02b (D05)	9.41 m	98.40 %	75.85 %	0.40 m	99.60 %	94.21 %
SM02c (T10)	9.67 m	100.00 %	76.05 %	0.46 m	100.00 %	94.01 %

Tableau 2. Performances des stratégies SM02a, SM02b et SM02c pour les algorithmes SPP et PPP évaluées à l’aide du logiciel RTKLIB durant un épisode expérimental marqué par des scintillations ionosphériques sévères à la station ISMR de Inconfidentes au Brésil. La stratégie SM02a est basée sur un masque spatial calculé à partir des skymaps de type GOS. Les stratégies SM02b et SM02c implémentent respectivement un tampon spatial de 5° et un tampon spatial 5° ajouté à un tampon temporel de 10 minutes.

B. Comparaison des différentes stratégies développées

49Au cours de plusieurs épisodes expérimentaux caractérisés par des effets sévères de scintillations ionosphériques observés à la station de Inconfidentes au Brésil, nous avons évalué les différentes stratégies d’atténuation pour les algorithmes SPP et PPP développées et décrites dans le cadre de cet article. Nous proposons ici une comparaison globale reposant sur trois critères de performance. Ces trois critères ont déjà été évoqués brièvement précédemment, il s’agit de l’exactitude, de la continuité et de la fiabilité de la solution de navigation calculée par les algorithmes de positionnement par satellites. L’exactitude de la solution est évaluée en considérant l’erreur entre la solution calculée et la vraie solution de référence. L’exactitude est mesurée au moyen du paramètre RMSE (Root Mean Square Error). La continuité de la solution représente la capacité d’un algorithme à fournir une solution valide de manière continue. La continuité est mesurée comme le taux de réussite d’un algorithme en termes de proportions d’époques associées à une solution valide. Enfin, la fiabilité d’un algorithme de positionnement par satellites représente sa capacité à fournir une solution d’exactitude donnée. En particulier, dans le cadre de cette recherche, nous mesurons la fiabilité des algorithmes SPP et PPP par le biais des paramètres SR₁₀ et SR_0.5, qui constituent les taux de réussite des algorithmes à fournir une solution avec une erreur inférieure à 10 m et 0.5 m, respectivement. Ces derniers paramètres permettent, contrairement au RMSE, de comparer valablement différentes stratégies caractérisées par des taux de réussite très différents.

50Comme l’illustre la Figure 16, presque toutes les stratégies d’atténuation développées et décrites dans le cadre de cet article contribuent à améliorer les performances des algorithmes SPP et PPP en termes d’exactitude, de continuité et de fiabilité lors d’épisodes de scintillations ionosphériques sévères.

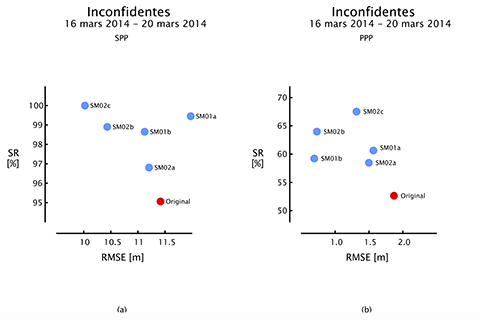
Figure 16. Comparaison des stratégies d'atténuation visant à améliorer les performances des algorithmes de positionnement par satellites SPP (gauche) et PPP (droite) durant plusieurs épisodes expérimentaux marqués par des effets sévères de scintillations ionosphériques à la station d’Inconfidentes au Brésil en mars 2014. Les différentes stratégies prototypées dans le cadre de cette recherche sont positionnées sur les graphiques ci-dessus en fonction de leurs performances en termes d’exactitude (RMSE – Root Mean Square Error) et de continuité (SR – Success Rate).

51Pour l’algorithme SPP, toutes les stratégies augmentent le taux de réussite - déjà élevé par ailleurs - qui atteint même la valeur maximale de 100 % pour la stratégie SM02c caractérisée par un tampon spatio-temporel basé sur les skymaps de type GOS. Cela révèle que les skymaps de type GOS ciblent avec succès les satellites dont les signaux sont affectés par des scintillations ionosphériques. En termes d’exactitude, il est très intéressant de souligner que toutes les stratégies d’atténuation dépassent la stratégie SM01a qui repose sur un masque horizontal isotrope de 15°. Comme évoqué précédemment, ce masque ne s’adapte pas aux conditions de scintillation rencontrées et il tend donc à supprimer abusivement certaines mesures tout en diminuant la qualité de la géométrie satellitaire. Ceci prouve les avantages de l’utilisation de skymaps de scintillations ionosphériques dans le but de construire des masques spatiaux en vue d’améliorer les performances des algorithmes de positionnement par satellites en cas de scintillations ionosphériques.

52Pour l’algorithme PPP, toutes les stratégies d’atténuation améliorent les performances en cas de scintillations ionosphériques en termes d’exactitude, de continuité et de fiabilité. En termes de continuité, la meilleure stratégie est la stratégie SM02c basée sur le tampon spatiotemporel. Ceci peut s’expliquer par le fait que cette stratégie réduit fortement le risque d’inclure des mesures de phase discontinues dans le processus d’estimation de paramètres de l’algorithme qui est basé sur un filtre de Kalman. Cependant, même cette stratégie ne parvient pas à assurer un taux de réussite de l’algorithme PPP supérieur à 67.52 % au cours des épisodes expérimentaux caractérisés par des conditions de scintillation ionosphérique sévères. Cela souligne d’une part qu’une marge d’amélioration significative existe encore et, d’autre part, que les masques spatiaux pourraient être combinés à d’autres techniques d’atténuation afin d’améliorer encore les performances de l’algorithme PPP en cas de scintillations ionosphériques sévères. Ceci est confirmé par le classement des stratégies basé sur le paramètre SR_0.5 illustré à la Figure 17.

Prototype Strategy	SPP			PPP
	RMSE	SR	SR10	RMSE	SR	SR0.5
Original	11.42 m	95.06%	45.11%	1.87 m	52.64%	31.74%
SM01a (EL15)	11.97 m	99.45%	48.45%	1.57 m	60.63%	43.51%
SM01b (AZEL)	11.12 m	98.65%	52.99%	0.69 m	59.23%	43.61%
SM02a (D01)	11.21 m	96.81%	51.10%	1.50 m	58.48%	43.36%
SM02b (D05)	10.43 m	98.90%	58.63%	0.73 m	63.97%	42.52%
SM02c (T10)	10.02 m	100.00%	64.37%	1.32 m	67.52%	42.02%

Tableau 3. Comparaison des stratégies d'atténuation visant à améliorer les performances des algorithmes de positionnement par satellites SPP et PPP durant plusieurs épisodes expérimentaux marqués par des effets sévères de scintillations ionosphériques à la station d’Inconfidentes au Brésil en mars 2014. Les différentes stratégies prototypées dans le cadre de cette recherche sont évaluées selon leurs performances en termes d’exactitude (RMSE – Root Mean Square Error), de continuité (SR – Success Rate) et de fiabilité (SR_XX).

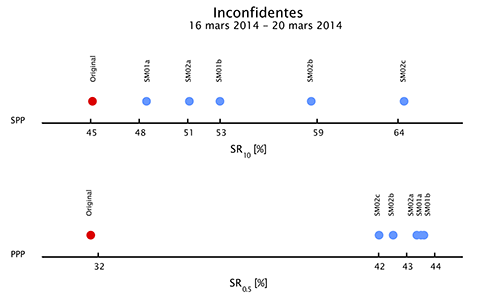
Figure 17. Classement des stratégies d'atténuation visant à améliorer les performances des algorithmes de positionnement par satellites SPP (haut) et PPP (bas) durant plusieurs épisodes expérimentaux marqués par des effets sévères de scintillations ionosphériques à la station d’Inconfidentes au Brésil en mars 2014. Les différentes stratégies prototypées dans le cadre de cette recherche sont positionnées sur ce graphique en fonction de leurs performances en termes de fiabilité. La fiabilité des algorithmes SPP et PPP est mesurées par le biais des paramètres SR10 et SR0.5 qui mesurent le taux de réussite des deux algorithmes à fournir une solution de navigation avec une erreur inférieure à 10 m et 0.5 m, respectivement.

Conclusion

53Dans cet article, nous avons montré comment des techniques d’analyse spatiale peuvent être exploitées sur des mesures ISMR et GNSS afin de déterminer les caractéristiques spatiotemporelles de scintillations ionosphériques équatoriales. En particulier, nous avons exploité l’indice d’autocorrélation spatial locale de Getis-Ord (Gi*) afin de construire des cartes représentant les effets de scintillations ionosphériques dans le ciel d’un utilisateur. L’objectif de l’élaboration de ces cartes est de permettre l’assimilation des caractéristiques spatiotemporelles des scintillations ionosphériques au sein d’algorithmes de positionnement par satellites tels que le Standard Point Positioning (SPP) ou le Precise Point Positioning (PPP). Nous avons montré que les cartes de scintillations ionosphériques peuvent être directement utilisées pour construire le modèle stochastique des algorithmes SPP et PPP et que cette technique permet d’améliorer les performances du positionnement par satellites SPP et PPP en termes d’exactitude, de continuité et de fiabilité.

Remerciements

54La recherche doctorale décrite dans cet article a été financée par le Fonds National de la Recherche Scientifique (FNRS) belge, le Sénat de Belgique par le prix ODISSEA et l’Université de Liège (ULiège) par le prix DEHAY. Elle a été menée au sein de l’Unité de Géomatique de l’Université de Liège (ULiège) en Belgique, en collaboration avec le Nottingham Geospatial Institute (NGI) de l’Université de Nottingham (UoN) au Royaume-Uni.

55Nous souhaitons exprimer notre gratitude à la Faculté des Sciences et Technologies (FST) de l’Universidade Estadual Paulista (UNESP) au Brésil, pour nous avoir autorisé l’accès aux données GNSS et ISMR des projets CIGALA et CALIBRA. Nous remercions également Mme C. Timmermans, chargée de Cours au Département de Mathématiques de l’Université de Liège, pour ses conseils avisés concernant la présentation et le calcul de certains paramètres statistiques.

BIBLIOGRAPHIE

56Aquino, M., Dodson, A.H., Souter, J., & Moore, T. (2007). Ionospheric Scintillation Effects on GPS Carrier Phase Positioning Accuracy at Auroral and Sub-Auroral Latitudes. In P. Tregoning and C. Rizos (Eds.), Dynamic Planet: Monitoring and Understanding a Dynamic Planet with Geodetic and Oceanographic Tools, IAG Symposium Cairns, Australia 22-26 August, 2005, Springer Berlin Heidelberg, p. 859-866, DOI: 10.1007/978-3-540-49350-1_121

57Aquino, M., Monico, J.F.G., Dodson, A.H., Marques, H., De Franceschi, G., Alfonsi, L., Romano, V. & Andreotti, M. (2009). Improving the GNSS Positioning Stochastic Model in the Presence of Ionospheric Scintillation. Journal of Geodesy, 83(10), 953-966. DOI: 10.1007/s00190-009-0313-6

58Baarda, W. & Netherlands Geodetic Commission (1967). Statistical concepts in geodesy. Delft: Rijkscommissie voor Geodesie, 74 p.

59Choy, S., Bisnath, S. & Rizos, Chr. (2017). Uncovering Common Misconceptions in GNSS Precise Point Positioning and Its Future Prospect. GPS Solutions, 21(1), 13-22. DOI: 10.1007/s10291-016-0545-x

60Conker, R.S., Bakry El-Arini, M., Hegarty, Chr. J., & Hsiao, T. (2003). Modeling the Effects of Ionospheric Scintillation on GPS/Satellite-Based Augmentation System Availability. Radio Science, 38(1), 1-1-1-23. DOI: 10.1029/2000RS002604

61da Silva, Alves H., de Oliveira Camargo, P., Galera Monico, J.F., Aquino, M., Marques, H.A, De Franceschi, G. & Dodson, A. (2010). Stochastic Modelling Considering Ionospheric Scintillation Effects on GNSS Relative and Point Positioning. Advances in Space Research, 45(9), 1113-1121. DOI: 10.1016/j.asr.2009.10.009

62Davies, K. (1990). Ionospheric Radio. Peter Pere. London: The Institution of Engineering and Technology, 600 p.

63Deo, M. & El-Mowafy, A. (2016). Triple-Frequency GNSS Models for PPP with Float Ambiguity Estimation: Performance Comparison Using GPS. Survey Review, 50(360), 249-261. DOI: 10.1080/00396265.2016.1263179

64Dow, J.M., Neilan, R. E. & Rizos, C. (2009). The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems. Journal of Geodesy, 83(3), 191-198. DOI: 10.1007/s00190-008-0300-3

65ESRI. https://pro.arcgis.com/fr/pro-app/tool-reference/spatial-statistics/h-how-hot-spot-analysis-getis-ord-gi-spatial-stati.htm

66Hamel, P., Sambou, D.C., Darces, M., Beniguel, Y. & Hélier, M. (2014). Kriging Method to Perform Scintillation Maps Based on Measurement and GISM Model. Radio Science, 49(9), 746-752. DOI: 10.1002/2014RS005470

67Hartmann, G. K. & Leitinger, R. (1984). Range Errors due to Ionospheric and Tropospheric Effects for Signal Frequencies above 100 MHz. Bulletin Géodésique, 58(2), 109-136. DOI: 10.1007/BF02520897

68Héroux, P. & Kouba, J. (2001). GPS Precise Point Positioning Using IGS Orbit Products. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 26(6-8), 573-578. DOI: 10.1016/S1464-1895(01)00103-X

69Hofmann-Wellenhof, B., Lichtenegger, H. & Wasle, E. (2008). GNSS – Global Navigation Satellite Systems - GPS, GLONASS, Galileo, and More. Springer Wien New-York, 470 p.

70Kieft, P., Aquino, M. & Dodson, A. (2014). Using Ordinary Kriging for the Creation of Scintillation Maps. In R. Notarpietro, F. Dovis, G. De Franceschi, and M. Aquino (Eds.) Mitigation of Ionospheric Threats to GNSS, Rijeka: IntechOpen. DOI: 10.5772/58781

71Kintner, P.M., Ledvina, B.M. & de Paula, E.R. (2007). GPS and Ionospheric Scintillations. Space Weather 5(9), S09003-1-23. DOI: 10.1029/2006SW000260

72Kintner, P.M., Humphreys, T. & Hinks, J. (2009). GNSS and Ionospheric Scintillation. InsideGNSS, 22-30. http://insidegnss.com/auto/julyaug09-kintner.pdf

73Lassudrie-Duchesne, P., Beniguel, Y., Bourdillon, A., Fleury, R., Valette, J-J., Minh, L.H. & Lan, T.T. (2010). Les effets de la scintillation ionosphérique sur le GPS. Institut Mine-Télécom, Télécom Bretagne, 18 p.

74Laurichesse, D., Mercier, F., Berthias, J-P., Broca, P. & Cerri, L. (2009). Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination. Navigation, 56(2), 135-149. DOI: 10.1002/j.2161-4296.2009.tb01750.x

75Leick, A., Rapoport, L. & Tatarnikov, D. (2015). GPS Satellite Surveying. 4th ed. Wiley, 807 p. DOI: 10.1002/9781119018612

76Lentz, J. (2009). Getis-Ord General G. Notes de cours. http://jenniferalentz.info/Teaching/StudyGuides/SpatialAutocorrelation.pdf

77Li, B., Lou, L. & Shen, Y. (2016). GNSS Elevation-Dependent Stochastic Modeling and Its Impacts on the Statistic Testing. Journal of Surveying Engineering, 142(2), 04015012. DOI: 10.1061/(ASCE)SU.1943-5428.0000156

78Lonchay, M. (2019). Ingestion of Ionospheric Scintillation Skymaps into GNSS Algorithms. Thèse de doctorat en Sciences, Université de Liège.

79Luo, X., Mayer, M. & Heck, B. (2009). Improving the Stochastic Model of GNSS Observations by Means of SNR-based Weighting. In M. G. Sideris (Ed.) Observing Our Changing Earth, International Association of Geodesy Symposia, Berlin, Heidelberg: Springer Berlin Heidelberg, p. 725-734.

80Park, J., Vadakke, V.S., Aquino, M., Yang, L. & Cesaroni, C. (2017). Mitigation of Ionospheric Effects on GNSS Positioning at Low Latitudes. Navigation, 64(1), 67-74. DOI: 10.1002/navi.177

81Subirana, S.J., Juan Zornoza, J.M. & Hernández-Pajares, M. (2013). In K. Fletcher (Ed.) GNSS Data Processing. Volume I: Fundamentals and Algorithms, ESA Communications, 268 p. http://www.gage.upc.edu/gnss_book

82SBAS Ionospheric Working Group (2010). Effects of Ionospheric Scintillations on GNSS. Stanford GPS Lab, Aeronautics & Astronautics Department, 22 p. https://gps.stanford.edu/resources/SBAS-IWG

83Sreeja, V., Aquino, M. & Elmas, Z.G. (2011). Impact of Ionospheric Scintillation on GNSS Receiver Tracking Performance over Latin America: Introducing the Concept of Tracking Jitter Variance Maps. Space Weather, 9(10), S10002-1-6. DOI: 10.1029/2011SW000707

84Susi, M., Aquino, M., Romero, R., Dovis, F. & Andreotti, M. (2014a). Design of a Robust Receiver Architecture for Scintillation Monitoring. In 2014 IEEE/ION Position, Location and Navigation Symposium - PLANS 2014, p. 73-81. DOI: 10.1109/PLANS.2014.6851359

85Susi, M., Andreotti, M., Aquino, M. (2014b). Kalman Filter Based PLL Robust Against Ionospheric Scintillation. In R. Notarpietro, F. Dovis, G. De Franceschi, and M. Aquino (Eds.) Mitigation of Ionospheric Threats to GNSS, Rijeka: IntechOpen. DOI: 10.5772/58769

86Susi, M., Andreotti, M., Aquino, M. & Dodson, A. (2017). Tuning a Kalman Filter Carrier Tracking Algorithm in the Presence of Ionospheric Scintillation. GPS Solutions, 21(3), 1149-1160. DOI: 10.1007/s10291-016-0597-y

87Takasu, T. (2013). RTKLib Ver. 2.4.2 Manual. http://www.rtklib.com/rtklib_document.htm

88Takasu, T. (2016). RTKLIB: An Open Source Program Package for GNSS Positioning. Retrieved August 31. http://www.rtklib.com/

89Tao L., Lachapelle, G. & Paulo Souto Fortes, L. (2014). Ionospheric Scintillation. Inside GNSS, January-February, 26-34.

90Wanninger, L. (1993). Effects of the Equatorial Ionosphere on GPS. GPS World, 4(7), 48-52.

91Warnant, R., Foelsche, U., Aquino, M., Bidaine, B., Gherm, V., Mainul Hoque, M., Kutiev, I., Lejeune, S., Luntama, JP., Spits, J., Strangeways, H.J., Wautelet, G., Zernov, N. & Jakowski, N. (2009). Mitigation of Ionospheric Effects on GNSS. Annals of Geophysics, 52(3-4), 373-390. 10.4401/ag-4585

92Wübbena, G., (1985). Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements. Proceedings of 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA., pp. 403-412.

93Zhang, X., Guo, F. & Zhou, P. (2014). Improved Precise Point Positioning in the Presence of Ionospheric Scintillation. GPS Solutions, 18(1), 51-60. DOI: 10.1007/s10291-012-0309-1

94Zumberge, J.F., Heflin, M.B., Jefferson, D.C., Watkins, M.M. & Webb, F.H. (1997). Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. Journal of Geophysical Research, 102(B3), 5005-5017. DOI: 10.1029/96JB03860

Pour citer cet article

A propos de : Matthieu LONCHAY

A propos de : René WARNANT