Yves CORNET, Matthieu LONCHAY, Jean-Paul KASPRZYK, Marie TROTTA & Marc BINARD

Brève note explicative des illustrations de la couverture

Table des matières

1Trois des quatre illustrations de la page de garde méritent certainement une brève explication technique et scientifique. Seule l’illustration notée 1 sur la Figure 1 ne nécessite pas cette explication car elle est extraite de l’article de Matthieu Lonchay et René Warnant publié dans ce numéro spécial du Bulletin de la Société Géographique de Liège (Lonchay et Warnant, 2019, sous presse). Il s’agit de la Figure 11 de cet article.

2Deux des trois autres illustrations sont aggrandies ci-dessous et accompagnées d’une légende (Figures 2 et 3). Elles sont extraites des deux dernières thèses de doctorat dirigées par Jean-Paul Donnay. Il s’agit des illustrations notées 2 et 3 (Figure 1). L’illustration notée 4 est une mosaique d’images-satellite du territoire belge que Marc Binard et Yves Cornet ont réalisée pour l’édition 2018 du Grand Atlas de Belgique (Charlier et Charlier-Vanderschraege, 2018).

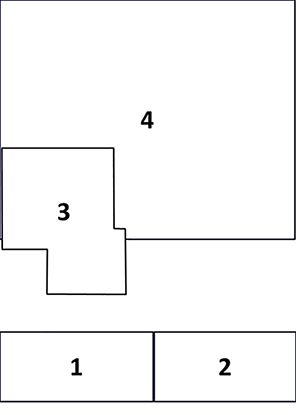
Figure 1. Shéma montrant la disposition des quatre illustrations de la page de garde

I. Illustration 1

3Il s’agit de la Figure 11 de l’article de M. Lonchay et R. Warnant publié dans ce numéro spécial d’hommage au Professeur Jean-Paul Donnay.

II. Illustration 2

4Cette illustration est extraite de la thèse de doctorat de Jean-Paul Kasprzyk (Kasprzyk, 2015) qui traite de l’informatique décisionnelle (Business Intelligence). L’informatique décisionnelle est une discipline permettant l’analyse efficace de grands jeux de données multidimensionnelles (entrepôts de données) pour l’aide à la décision. En particulier, les outils SOLAP (Spatial OnLine Analytical Processing) offrent une navigation intuitive aux décideurs dans des cubes de données spatiaux à travers des cartes, des tableaux et des graphiques interactifs. Les différentes représentations des données sont notamment calculées grâce à des opérations de forage et de coupe. Les forages agrègent les données à différents niveaux hiérarchiques d’une dimension de sorte à modifier la granularité de cette dernière. Par exemple, un graphique peut représenter un nombre de délits par jour (niveau temporel 1), par mois (niveau temporel 2) ou par trimestre (niveau temporel 3). Les coupes fixent les agrégations sur une modalité particulière d’une ou plusieurs dimension(s). Par exemple, une double coupe sur les dimensions « type de délit » et « ville » peut générer une représentation des cambriolages à Londres.

5Les SOLAP peuvent être enrichis de nombreuses fonctionnalités issues du domaine des SIG pour la gestion et la représentation des dimensions spatiales. Il est par exemple possible de produire des cartes de densités de délits dans un espace continu (cartes de chaleur ou Kernel Density Estimation - KDE) afin de mieux planifier la répartition spatiale des patrouilles de police en fonction du temps et du type de délit. La Figure 2 montre l’évolution de la densité de cambriolages entre le premier et le second trimestre 2012 à Londres. Elle résulte de la différence (opération d’algèbre de carte) entre une coupe A (premier trimestre) et B (second trimestre) d’un cube de données raster.

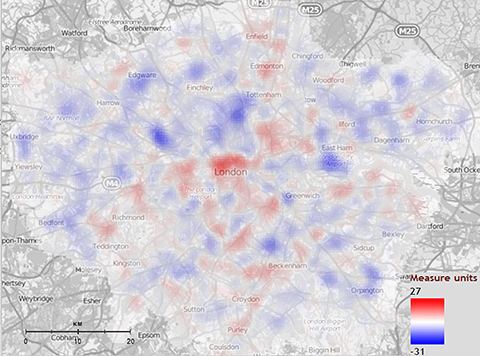
Figure 2. Évolution de la densité de cambriolages entre le premier et le second trimestre 2012 à Londres (source : Kasprzyk, 2015) ; la variable représentée est une différence de deux scores ; chacun d’eux indique la densité de délits relative à une fonction KDE et une bande passante (bandwidth - déterminant l’importance du lissage) donnés ; c’est la raison pour laquelle, comme pour cette différence, des KDE ne peuvent être agrégés que s’ils partagent la même fonction KDE et la même bande passante.

III. Illustration 3

6Cette illustration est constituée de deux figures extraites de la thèse de doctorat de Marie Trotta (Trotta, 2014) qui porte sur le profilage géographique et plus particulièrement le développement et l’application de méthodes originales d’analyse spatiale dans ce domaine particulier des sciences géographiques. Dans sa thèse, Marie Trotta a notamment mis au point une méthode basée sur la mesure de distance-coût sur le réseau routier depuis les lieux d’actes criminels (agressions sexuelles) associés à un même individu par l’enquête judiciaire. Cette méthode permet de modéliser la variation spatiale du coût de déplacement moyen et de sa variance en diminuant l’impact des observations individuelles grâce à un protocole basé sur le principe du jacknife.

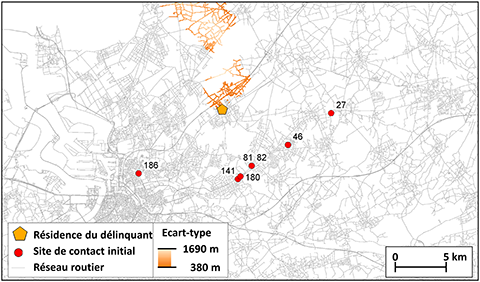
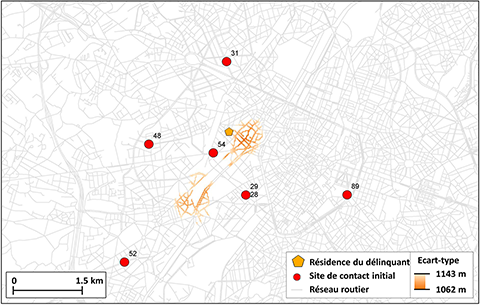
Figure 3. Détermination, pour deux séries de viols en série, d’une région de recherche en appliquant l’hypothèse de variance minimum de la distance-coût ; estimation par la méthode du jacknife pour réduire l’influence des observations individuelles (source : Trotta, 2014).

7Les deux cartes de la Figure 3 montrent les résultats de la deuxième procédure. Cette procédure permet de déterminer la zone préférentielle sur laquelle orienter les investigations policières, soit celle qui minimise la variance. Cette hypothèse de minimisation de variance est justifiée par un fait d’observation du comportement spatial des violeurs en série. Généralement, ils commettent leurs crimes en réalisant des déplacements dont la distance est homogène par rapport à un point d’ancrage (résidence, cache, lieu de travail …) tout en évitant une zone trop proche de celui-ci où ils pourraient plus facilement être identifiés par des connaissances. Par ailleurs, cette technique permet de modéliser les déplacements avec direction préférentielle de l’agresseur contrairement aux approches classiques de surfaces de potentiel basées sur la décroissance de probabilité avec la distance. La première des deux cartes montre une séquence d’actes commis par un individu n’agissant qu’au sud de sa résidence, attiré par des lieux plus favorables à la rencontre de victimes. Contrairement à ce qui est obtenu par les méthodes minimisant la distance moyenne parcourue, la minimisation de variance met en évidence, dans ce cas, une zone cible en dehors du polygone convexe de Hull. L’autre exemple a permis de déterminer deux zones cibles à l’intérieur du polygone de Hull.

IV. Illustration 4

8L’illustration 4 est une mosaïque de 10 images-satellite (Tableau 1) enregistrées par le capteur OLI à bord de Landsat 8. Les canaux OLI 2 (bleu), OLI 3 (vert) et OLI 4 (rouge) ont été utilisés pour réaliser la composition colorée en vraie couleur. Après avoir contrôlé la cohérence géométrique des produits de niveau L1TP (Precision Terrain - ≤ 12m de RMSE radiale) downloadés sur le site Earth Explorer de l’USGS (https://earthexplorer.usgs.gov), nous les avons tous réchantillonnés dans un même carroyage du système de référence cartographique Lambert 72 belge.

9Ensuite, une procédure originale de normalisation radiométrique relative a été appliquée. Les images voisines d’un même path et acquises le même jour ont d’abord été assemblées (1, 2 et 3 dans le Tableau 1). L’assemblage central (1) a été utilisé comme référence radiométrique. Pour normaliser la radiométrie des autres images assemblées ou non, nous avons tout d’abord réalisé, pour chaque image ou assemblage, y compris celui de la référence, le masque des pixels nuageux et aqueux en utilisant une bande de metadonnées spatiales évaluant de la qualité (bande BQA).

Row	Path 199		PATH 198	PATH 197
24	8/5/2016 (2)		20/7/2016 (1)	14/6/2017 (3)
25	8/5/2016 (2)	27/5/2016 (7)	20/7/2016 (1)	14/6/2017 (3)
26	19/5/2014 (6)		10/4/2014 (5)	6/6/2014 (4)

Tableau 1. Images utilisées par date, path (199 à 197, d’ouest en est) et row (24 à 26, du nord au sud)

10Dans la zone commune à chaque couple de produits considéré (2-1, 3-1, 5-1 puis 4-3, 6-2 et 7-2) et sur les seuls pixels sélectionnés par la combinaison des masques calculés précédemment sur les deux éléments du couple, nous avons extrait une matrice de corrélations temporelles pour chacune des bandes aux deux dates considérées. Chacune des trois matrices, une pour OLI 2, une pour OLI 3 et une pour OLI 4, obtenue par couple, a constitué la donnée d’entrée à une analyse en composantes principales. Le score factoriel standardisé obtenu sur la seconde composante exprime l’importance du changement de la signature entre les deux dates pour la bande spectrale considérée. Le seuillage du score factoriel (on ne conserve que les valeurs proches de 0) des trois secondes composantes calculées à partir des trois paires de bandes homologues a permis de sélectionner les invariants radiométriques (pseudo invariant features). Un pixel a été considéré comme invariant radiométrique si son score factoriel sur la seconde composante est proche de 0 dans les trois cas. En exploitant ces pixels invariants radiométriques non aqueux ni nuageux, nous avons ajusté la fonction linéaire de normalisation radiométrique relative pour chaque canal entrant dans la composition colorée et correspondant à chaque couple de produits considéré.

11Cette procédure a permis de contraster au maximum la composition colorée de la mosaïque finale tout en minimisant la perception des limites entre images ou assemblages d’images. Néanmoins, quelques variations phénologiques sont perceptibles au centre de la mosaïque. Elles résultent de l’acquisition printanière précoce de l’image 198/26 du 10/4/2014 (5) et estivale tardive de l’assemblage 1 (images 198/24 et 25 du 20/7/2016). Elles ont été placées en arrière plan. L’importance variable de la surface couverte en sols nus entre les différents mois selon l’avancement relatif à l’année considérée du cycle phénologique est aussi visible, surtout dans la partie sud de la mosaïque en dehors du territoire belge dans le bassin parisien. Enfin, remarquons que l’image 199/25 du 27/5/2016 (7) a été utilisée pour compléter les pixels nuageux apparaissant dans son homologue du 8/5/2016 (2).

12La procédure décrite de façon très synthétique dans cette note n’a jamais été publiée. Elle a été utilisée pour produire d’autres mosaïques, une mosaïque en vraie couleur de la Suisse où nous avons combiné des images enregistrées par les capteurs TM et OLI, respectivement à bord de Landsat 5 et 8 (Charlier et Charlier-Vanderschraege, 2017) et une autre en fausse couleur infra-rouge de la Belgique (Charlier et Charlier-Vanderschraege, 2015).

BIBLIOGRAPHIE

13Charlier J. & Charlier-Vanderschraege D. (2015). Le petit atlas. Éditions De Boeck Éducation , Louvain-la-Neuve, 7^ème édition.

14Charlier J. & Charlier-Vanderschraege D. (2017). Atlas de la Suisse, de l'Europe et du monde. Éditions De Boeck Éducation, Louvain-la-Neuve, 4^ème édition.

15Charlier J. & Charlier-Vanderschraege D. (2018). Le grand atlas : de la 1^ère à la 6^ème secondaire. Éditions De Boeck Éducation, Louvain-la-Neuve, 15^ème édition.

16Kasprzyk J. P. (2015). Intégration de la continuité spatiale dans la structure multidimensionnelle d’un entrepôt de données - SOLAP raster. Thèse de doctorat en Sciences, Université de Liège, 247 p. + xxxii, https://orbi.uliege.be/bitstream/2268/182360/

17Lonchay M. & Warnant R. (2019, sous presse). Intégration de cartes de scintillations ionosphériques dans des algorithmes de positionnement par satellites. Bulletin de la Société Géographique de Liège, 72.

18Trotta M. (2014). Modelling serial offenders’ spatial behaviours: new assumptions for geographic profiling. Thèse de doctorat en Sciences, Université de Liège, 238 p., http://bictel.ulg.ac.be/ETD-db/collection/available/ULgetd-10162014-103102/

Pour citer cet article

A propos de : Yves CORNET