Xavier FETTWEIS, Bruno AMBROISE, Pierre-Marie DAVID, Nicolas GHILAIN, Patrice PAUL & Cyril WUEST

Évolution actuelle (1960-2021) de l’enneigement dans les Vosges à l’aide du modèle régional du climat MAR

Résumé

L’évolution actuelle de l’enneigement dans les Vosges (N-E de la France) a été simulée à une résolution de 4 km avec le modèle régional du climat MAR (version 3.13) forcé par les réanalyses ERA5. Moyennant un petit ajustement de seulement 3 paramètres (dont 1 °C d’augmentation du seuil de température neige/pluie), MAR a été optimisé et validé sur 5 et 8 hivers (DJF) par rapport à des observations quotidiennes (température, précipitation, hauteur de neige). Sur les 62 hivers (DJF) 1960-2021, MAR suggère une diminution significative statistiquement d’environ un facteur deux de la hauteur moyenne de neige, due à l’augmentation significative des températures (~+2 °C/62 ans). Bien que les précipitations aient légèrement augmenté (+10-20 %/62 ans) à cause d’un renforcement (non significatif) de la circulation d’ouest, elles tombent de plus en plus sous forme de pluie, en particulier en dessous de 1000 m. Au-dessus de 1000 m, il ne neige pas moins qu’avant mais il y a plus de fonte réduisant le manteau neigeux entre deux événements neigeux. En extrapolant les tendances actuelles, une anomalie de +2.5 °C (resp. +3.8 °C) par rapport aux hivers 1960-90 serait suffisante pour ne plus avoir de neige en moyenne en-dessous de 750 m (resp. 1000 m).

Abstract

The current evolution of snow cover in the Vosges (N-E of France) was simulated at a resolution of 4 km with the regional climate model MAR (version 3.13) forced by the ERA5 reanalysis. Thanks to the adjustment of only 3 parameters (including a 1°C increase of the snow/rain temperature threshold), MAR was optimized and validated over 5 and 8 winters (DJF) with respect to daily observations (temperature, precipitation, height of the snowpack). Over the 62 winters (DJF) 1960-2021, MAR suggests a statistically significant decrease of about a factor of two in the average snow depth due to the significant increase in temperatures (~+2°C/62 years). Although precipitation has slightly increased (+10-20%/62 years) due to a non-significant strengthening of the westerly circulation, it falls more and more in the form of rain, especially below 1000 m. Above 1000 m, it does not snow less than before but there is more melting reducing the snowpack between two snow events. By extrapolating current trends, an anomaly of +2.5°C (resp. +3.8°C) compared to the winters of 1960-90 would be sufficient to no longer have snowpack on average below 750m (resp. 1000m).

Table des matières

Introduction

1Séparées par la vallée du Rhin, les Vosges (au Nord-Est de la France) et la Forêt Noire (au Sud-Ouest de l’Allemagne) sont deux massifs de moyenne montagne avec plusieurs sommets culminant à plus de 1350 m. Bénéficiant d’un enneigement suffisant en hiver jusqu’à maintenant (Juillard, 1954 ; Paul, 1984), ces massifs ont vu dans les années 1950-60 le développement de nombreuses stations de ski (dont une dizaine dans les Vosges), avec des pistes typiquement entre 750 et 1250 m d’altitude. Malheureusement, comme un peu partout en France, ces stations ont souffert lors de plusieurs hivers récents d’un manque d’enneigement suite au réchauffement climatique (Martin et Etchevers, 2005 ; Beaumet et al., 2021), à tel point que certaines stations (comme celle du Ventron à 870-1100 m dans les Vosges) ont déjà décidé de fermer définitivement.

2Malgré sa réduction observée et son impact sur l’avenir de ces stations, l’évolution récente de l’enneigement dans les Vosges a encore été très peu étudiée et les quelques études disponibles concernent certains sites d’altitude (Wahl et al., 2009) et ne considèrent pas les Vosges dans leur ensemble ni les tranches d’altitude concernées par ces stations de ski. C’est pourquoi cette étude porte sur l’évolution de l’enneigement à l’échelle du massif vosgien depuis les années 1960, à l’aide de la modélisation régionale du climat qui permet d’en avoir une estimation continue et homogène en toute région des Vosges.

3Pour ce faire, nous avons utilisé le modèle climatique régional MAR, développé au Laboratoire de Climatologie de l’Université de Liège. Ayant déjà bien fait ses preuves pour étudier l’évolution des calottes polaires (Fettweis, 2007 ; Fettweis et al., 2020), ce modèle a été récemment adapté avec succès au climat de l’Europe de l’Ouest, pour étudier notamment l’évolution actuelle et future de l’enneigement en Belgique (Wyard et al., 2017, 2021). Dans cette application aux Vosges, nous avons tout d’abord vérifié si, moyennant l’ajustement de quelques paramètres, ce modèle est bien capable de représenter correctement l’évolution des températures, précipitations et hauteurs de neige journalières enregistrées par plusieurs stations météorologiques représentatives de la variabilité climatique dans les Vosges.

4Une fois optimisé et validé localement selon une procédure classique (Klemes, 1986 ; Ambroise et al., 1995) déjà en partie appliquée dans Wuest (2021), le modèle MAR a permis de simuler à l’échelle des Vosges l’évolution depuis 1960 de l’enneigement ainsi que des températures et précipitations au sol qui le contrôlent. Même si les simulations MAR ont été faites en continu sur toute la période, seuls les résultats pour les 3 mois de l’hiver météorologique (Déc-Jan-Fév) sont présentés ici, sachant que l’enneigement parfois encore important observé en mars en altitude résulte alors d’un hiver qui a été lui aussi froid et neigeux, et que l’enneigement à basse altitude en dehors de ces 3 mois reste anecdotique.

I. Modélisation

A. Le modèle MAR

5Le modèle MAR (pour "Modèle Atmosphérique Régional"), dont la dernière version v3.13 a été utilisée ici, est détaillé succinctement dans l’Appendice 1. C’est un modèle hydrostatique simulant l’évolution temporelle et spatiale des température, vent, humidité et pression ainsi que des hydrométéores générant nuages et précipitations à l’intérieur d’un domaine d’intégration restreint et pour une résolution spatiale bien définie (Gallée et al., 1994). Il incorpore le module multicouche SISVAT de transfert énergétique et hydrique (de Ridder et Gallée, 1998) pour simuler en chaque pixel tous les processus de surface dans le système sol-neige-glace-végétation-atmosphère en tenant compte des types d’occupation du sol.

6Un des atouts de MAR par rapport aux autres modèles régionaux est son sous-module "Neige", basé sur le modèle CROCUS de Météo-France (Lafaysse et al., 2017). Il simule les processus et propriétés de la neige contrôlant l’évolution du manteau neigeux. Toute chute de neige crée une nouvelle couche de neige fraîche dont la densité initiale est l’un des paramètres du modèle. La partition neige-pluie (N/P) dans les précipitations totales simulées au sol se fait selon une transition linéaire entre -1 °C (100 % neige) et +1 °C (100 % pluie).

7Comme tous les modèles régionaux, MAR a besoin toutes les 6 heures d’un forçage en température, vent, humidité et pression à ses frontières latérales à chacun de ses niveaux verticaux. Il sera ici basé sur les réanalyses ERA5 du Centre Européen ECMWF. Disponibles à une résolution de 0.3° x 0.3° (soit environ 30 km x 30 km), elles permettent de reconstruire le climat observé depuis 1940.

8Les choix faits dans MAR (cf. Appendice 1) obligent (i) à considérer une zone de relaxation d’environ 20 pixels de large tout autour de notre domaine d’intérêt et (ii) à appliquer à l’humidité spécifique forcée aux frontières du MAR une correction relative qui augmente avec la résolution: +5 %, +7.5 % et +10 %, respectivement, pour des résolutions inférieures à 10 km, 7.5 km et 5 km.

B. Application au Massif vosgien

9Dans les Vosges, les plus forts contrastes climatiques sont observés le long d’un transect Ouest-Est passant par les Hautes-Vosges au climat montagnard (Paul, 1982) : la variabilité spatiale des températures dépend essentiellement de l’altitude locale; et celle des précipitations, de la distance à la crête, et donc aussi de l’altitude lissée. Ainsi, les précipitations diminuent fortement sur le versant alsacien, depuis plus de 2000 mm/an au-dessus de 1300 m jusqu’à 550 mm/an à moins de 200 m en plaine d’Alsace à cause d’un fort effet de foehn (Humbert et Paul, 1982). De ce fait, l’enneigement est important et durable dans les Hautes-Vosges mais faible et peu fréquent en plaine, avec souvent des successions d’épisodes d’enneigement plus ou moins longs aux altitudes intermédiaires. Enfin, même si l’essentiel des précipitations est associé à des perturbations de secteur ouest ou sud-ouest ou à des orages orographiques, certains épisodes importants sont liés à des situations de retour d’est (Paul et Roussel, 1985).

10En conséquence, le domaine d’intégration retenu pour MAR est centré sur les Hautes-Vosges, où l’enneigement est maximal. Il inclut les Vosges méridionales et centrales, la plaine rhénane ainsi qu’une partie du massif de la Forêt Noire (Figure 1). La résolution de 4 km retenue, plus fine que dans les précédentes applications de MAR sur la Belgique, reste encore compatible avec son hypothèse hydrostatique (négligeant l’accélération de la vitesse verticale dans la résolution des équations de Navier-Stokes). La zone de relaxation (~20 pixels dans les quatre directions) a été volontairement exclue des figures montrées ci-dessous.

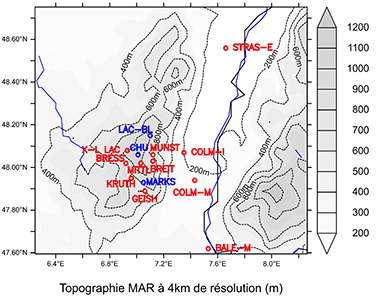
Figure 1. Topographie à 4 km de résolution du domaine simulé par MAR, avec localisation des 14 stations météorologiques utilisées dans cette étude. À noter : la zone de relaxation de 20 pixels de large entourant ce domaine n’y figure pas. Les 3 stations au-dessus de 1000 m sont affichées en bleu.

C. Procédure d’optimisation et validation

11Cette optimisation a porté sur seulement trois paramètres qui dans MAR contrôlent l’enneigement et les 2 principales variables dont il dépend (température, précipitations) : dans un premier temps, la correction d’humidité aux frontières, impactant surtout les précipitations totales simulées ; dans un deuxième temps, une fois MAR optimisé en température et précipitation, le(s) seuil(s) N/P de températures à 2 m et la masse volumique de la neige fraîche, impactant la hauteur de neige au sol simulée. Dans la configuration standard de MAR v3.13, l’humidité est augmentée de +10% pour une résolution de 5 km ou moins, les seuils de températures N/P sont -1 °C/+1 °C, la masse volumique de la couche créée pour la neige fraîche varie entre 50 et 200 kg/m3 en fonction de la température et de la vitesse de vent - comme dans le modèle CROCUS (Lafaysse et al., 2017).

12Elle a été réalisée au pas de temps journalier sur les 5 hivers (DJF) 2016-21 aux enneigements bien contrastés, par comparaison des simulations pour plusieurs configurations de MAR avec les observations de 12 stations météorologiques. Ces stations sont situées le long de 2 transects dans une large bande Ouest-Est centrée sur les Hautes-Vosges, et se prolongeant des 2 côtés de la crête des Vosges et en plaine d’Alsace (Figure 1, Tableau 1). À ces stations choisies pour être bien représentatives des principales situations topographiques et orographiques s’ajoutent 2 stations synoptiques de référence en plaine: Strasbourg-Entzheim (STRAS_E) et Bâle-Mulhouse (BALE_M).

13Cette optimisation a ensuite été validée, au moins localement, par des comparaisons du même type sur d’autres périodes et pour 2 stations nivo-météorologiques de référence, bien représentatives des contrastes spatiaux rencontrés : pour les Hautes-Vosges, la station X-L_CHU (la plus haute et la plus enneigée), au pas de temps journalier sur les 8 hivers (DJF) 1989-97 bien contrastés ; pour la plaine, la station STRAS-E, au pas de temps hivernal (DJF) sur les 62 hivers (DJF) 1960-2021 (incluant les 2 mois de janvier et février 2022). L’Appendice 2 précise les principales caractéristiques des données observées et simulées utilisées dans toutes ces comparaisons et évaluations du MAR.

14Avec la résolution de 4 km, l’altitude moyenne du pixel MAR correspondant à chaque station peut être sensiblement différente (jusqu’à 200 m d’écart) de son altitude locale. Les températures et hauteurs de neige simulées ont donc été corrigées de cette différence d’altitude à l’aide du gradient vertical calculé tous les jours à partir des 9 pixels MAR autour de la station. Ces corrections altitudinales des simulations améliorent légèrement à chaque fois la comparaison aux observations locales. Pour les précipitations, aucune correction d’altitude n’a été apportée, car les précipitations observées dépendent surtout de l’altitude lissée de la station, similaire donc à celle du pixel MAR correspondant. Par contre, comme expliqué dans l’Appendice 2, l’altitude du pixel MAR le plus haut, correspondant à la station XL-CHU (1220 m), a été artificiellement augmentée de 1095 m à l’altitude de la station pour optimiser la comparaison de l’enneigement (fortement dépendant de l’altitude) avec les observations in situ.

15Calculés par hiver (DJF) et par station puis moyennés sur tous les hivers et les 14 stations considérés ici, les critères statistiques retenus pour ces comparaisons sont le biais moyen, l’erreur quadratique moyenne centrée RMSEc (autrement dit, l’écart-type des biais) et le coefficient de corrélation R entre valeurs journalières simulées et observées. En modélisation du climat, les simulations d’un modèle sont considérées comme acceptables si le biais moyen et le RMSEc sont inférieurs à la variabilité journalière évaluée par l’écart-type STD des observations. De plus, des graphiques entre valeurs simulées et observées et les courbes de régression associées ont été utilisés pour identifier d’éventuelles tendances (et donc les biais systématiques du modèle) entre ces valeurs. Les valeurs nulles de précipitations et de hauteur de neige ont été prises en compte dans les comparaisons statistiques.

Station météo	Nom complet	ID	Altitude (m)	Altitude MAR (m)	Lat. (°N)	Long. (°E)	T (°C)	HN (cm)
Versant lorrain
X-L_LAC	Xonrupt-Longemer Lac Longemer	88531002	745	874	48.07	6.95		x
BRESS	La Bresse	88075005	772	759	48.01	6.94	x	x
Crêtes
X-L_CHU	Xonrupt-Longemer Chalet Univ. Chitelet	88531003	1220	(1220)	48.05	7.01	x	(x)
MARKS	Oderen Markstein	68247003	1184	998	47.92	7.03	x	x
LAC-BL	Orbey Lac Blanc	68249002	1080	1060	48.14	7.10	x	x
Versant alsacien
MITTL	Mittlach	68210002	552	759	48.01	7.03		x
BREIT	Breitenbach	68051001	466	663	48.02	7.10		x
MUNST	Munster	68226005	420	553	48.05	7.12	x
KRUTH	Kruth Barrage	68171002	512	701	47.94	6.96	x
GEISH	Geishouse	68102001	618	618	47.88	7.06	x
Plaine d'Alsace
COLM-I	Colmar INRA	68066001	202	202	48.03	7.33	x
COLM-M	Colmar Meyenheim	68205001	207	208	47.93	7.41	x	x
BALE-M	Bâle Mulhouse	68297001	263	265	47.61	7.51	x	x
STRAS-E	Strasbourg Entzheim	67124001	150	146	48.55	7.64	x	x

Tableau 1. Stations nivo-météorologiques utilisées pour optimiser et valider le modèle MAR sur les 5 hivers (DJF) 2016-21. Pour chaque station: référence, coordonnées, altitude, altitude du pixel MAR associé, disponibilité "x" des observations de température T et/ou de hauteur de neige HN. Toutes les stations ont des observations de précipitation (sauf X-L_CHU: cf. texte).

II. Résultats en optimisation et validation

A. Ajustement de la correction de l’humidité spécifique aux frontières

16La résolution de 4 km, plus fine que dans les précédentes applications de MAR, suggère une correction relative de l’humidité spécifique aux frontières un peu plus forte que les +10 % appliqués par défaut. Des simulations ont donc été réalisées en faisant varier la correction par paliers de +1 % ou +0.5 % entre la valeur initiale de +10 % et +14 % (Tableau 2a).

17Les températures journalières simulées aux 14 stations se sont avérées peu sensibles à l’augmentation de la correction, et leur comparaison avec les températures observées reste dans tous les cas excellente (R = 0.95) : le biais diminue faiblement, de -0.63 °C à -0.53 °C, avec un RMSEc à peu près constant de 1.39 °C. Comme attendu, les précipitations sont davantage sensibles à la correction: partant de -0.80 mm/j pour +10 % (sous-estimation), le biais augmente jusqu’à +0.31 mm/j (surestimation), tandis que le RMSEc augmente de 4.56 mm/j à 4.60 mm/j, en moyenne sur les 14 stations, avec dans tous les cas une corrélation un peu plus faible de 0.82 (Tableau 2a). À titre d’exemple, les résultats obtenus pour la correction de 12 % (Tableau 2b) sont détaillés ci-dessous.

18Pour les températures journalières simulées avec 12 %, on constate en moyenne sur les 14 stations un biais de -0.58 °C (sous-estimation), une corrélation de 0.95 et un RMSEc de 1.39 °C, soit seulement 33 % de la variabilité journalière (STD moyen) de la température observée à 2 m. Ces valeurs changent peu selon les stations. Pour la Belgique (Wyard et al., 2017), les simulations MAR sont aussi un peu trop froides en hiver. Même s’ils ne sont pas négligeables, ces biais sont acceptables par rapport à la précision numérique du modèle (0.2°C). Ces bonnes performances montrent ainsi la capacité de MAR à bien représenter l’évolution saisonnière de la température journalière dans toutes les situations topographiques présentes dans les Vosges.

19Pour les précipitations journalières simulées avec 12 %, la comparaison reste bonne. En moyenne sur les 14 stations, on constate un faible biais de -0.27 mm/j (sous-estimation), soit -6 % des précipitations observées, et une RMSEc de 4.53 mm/j, soit 53 % de leur variabilité journalière. Recevant beaucoup plus de précipitations, les stations de montagne ont des RMSEc plus importants que les stations de plaine. Par ailleurs, les biais simulés par station montrent: (i) une faible surestimation sur les crêtes - jusqu’à +1.4 mm/j pour la station MARKS, située sur un col très venteux, où ce biais doit en grande partie résulter d’un probable déficit local de captation des précipitations (surtout neigeuses); et (ii) une certaine sous-estimation sur les 2 versants – jusqu’à -2 mm/j pour les 2 stations MITTL et KRUTH, situées sous les crêtes au fond de vallées très encaissées où le gradient pluviométrique horizontal est très élevé. Ces 2 stations permettent ainsi de bien illustrer la difficulté qu’a encore MAR, comme probablement tout autre modèle régional, à simuler les précipitations pour ce type de situation topographique non résolue à cette résolution spatiale de 4 km, alors qu’elle est rencontrée dans nombre de vallées des Vosges et d’autres massifs montagneux.

20La corrélation moyenne de 0.82 pour les précipitations est un peu moins bonne que pour la température. C’est aussi le cas avec MAR au Groenland (Delhasse et al., 2020) ou en Belgique (Wyard et al., 2017; Doutreloup et al., 2019) et, de manière plus générale, avec tous les modèles du climat car la précipitation est une variable de “fin de chaîne” qui cumule les biais de toutes les autres variables (humidité, vent, température, nuage, …), contrairement à la température qui est une variable de base dans les équations physiques des modèles. Enfin, il est important de noter que la corrélation est surtout faible pour les stations peu arrosées de plaine (0.65-0.74) alors qu’elle atteint 0.9 pour les stations très arrosées de montagne dont on étudie l’évolution de l’enneigement.

21D’après les indices statistiques moyennés sur les 14 stations (Tableau 2a), les meilleurs résultats d’optimisation sont obtenus pour les corrections de +12.5 % puis de +12.0 %, avec des biais moyens respectifs de -0.13 mm/j et -0.27 mm/j. Toutefois, sans les 2 stations MITTL et KRUTH au fort impact sur ces biais du fait de leur situation particulière non résolue à la résolution du modèle, ces biais deviennent +0.19 mm/j et seulement +0.05 mm/j, respectivement. Ce biais quasiment nul suggère ainsi que la correction de +12.0 % est en fait la meilleure pour la plus grande partie du domaine. Donnant pour toutes les stations des résultats satisfaisants tant en température qu’en précipitation, c’est donc la correction relative de +12 % sur l’humidité forcée aux frontières latérales qui a été retenue pour la configuration optimisée de référence et qui a été appliquée dans toutes les simulations suivantes. Il est toutefois important de mentionner que les différences de performance entre ces 2 corrections restent négligeables par rapport aux précipitations moyennes (4.8 mm/j  +/- STD de 8.5 mm/j) et que choisir plutôt l’autre correction n’impacterait en rien l’analyse faite en Section 4.

a	analyse de sensibilité
	Température (°C) en hiver (DJF)					Précipitation (mm/j) en hiver (DJF)
Correction			Biais	RMSEc	R			Biais	RMSEc	R
10.00 %			-0.63	1.38	0.95			-0.80	4.56	0.82
11.00 %			-0.61	1.39	0.95			-0.56	4.54	0.82
11.50 %			-0.60	1.39	0.95			-0.41	4.54	0.82
12.00%			-0.58	1.39	0.95			-0.27	4.53	0.82
12.50 %			-0.57	1.39	0.95			-0.13	4.55	0.82
13.00 %			-0.56	1.39	0.95			0.02	4.56	0.82
14.00 %			-0.53	1.39	0.95			0.31	4.60	0.82
b	statistiques par station pour la correction optimisée de +12%
	Température (°C) en hiver (DJF)					Précipitation (mm/j) en hiver (DJF)
Station	Moy	STD	Biais	RMSEc	R	Moy	STD	Biais	RMSEc	R
X-L_LAC						7.61	12.29	-0.66	5.66	0.89
BRESS	1.87	3.91	-0.58	1.24	0.95	6.97	11.72	-0.84	5.47	0.89
X-L_CHU	-0.71	4.35	-0.75	1.75	0.92	7.61	12.29	0.52	5.44	0.90
MARKS	-0.13	4.55	-1.12	1.70	0.94	5.38	10.57	1.39	5.94	0.85
LAC-BL	0.56	4.47	-0.88	1.36	0.95	5.60	9.13	0.97	4.43	0.90
MITTL						8.16	14.23	-2.03	7.52	0.86
BREIT						4.73	8.96	-0.35	4.05	0.89
MUNST	3.20	4.35	0.14	1.44	0.94	4.09	8.02	-0.80	3.90	0.89
KRUTH	2.58	4.00	0.07	1.28	0.95	7.55	12.95	-2.05	6.52	0.88
GEISH	3.21	4.24	-1.20	1.26	0.96	3.96	6.99	0.13	4.57	0.80
COLM-I	3.94	4.22	-0.33	1.47	0.94	1.42	3.29	0.06	2.40	0.74
COLM-M	3.92	4.47	-0.55	1.36	0.95	1.15	2.79	0.37	2.58	0.67
BALE-M	3.78	4.21	-0.50	1.27	0.95	1.62	3.32	-0.31	2.68	0.65
STRAS-E	3.98	4.15	-0.70	1.34	0.95	1.50	3.01	-0.12	2.30	0.70
Moyenne	2.38	4.27	-0.58	1.39	0.95	4.81	8.54	-0.27	4.53	0.82

Tableau 2. Optimisation de MAR en température et précipitation journalières sur 14 stations météorologiques pour les 5 hivers (DJF) 2016-21 : ajustement de la correction relative de l’humidité spécifique aux frontières. a : statistiques globales (14 stations) de l’analyse de sensibilité à la correction. b : statistiques par station pour la correction optimisée (+12 %). Critères statistiques : moyenne Moy et écart-type STD observés ; Biais moyen, écart quadratique moyen centré RMSEc, coefficient de corrélation R entre valeurs simulées et observées. En gras : simulation de référence avec la correction optimisée à +12 %.

B. Ajustement de la partition neige-pluie et de la masse volumique de la neige fraîche

22En augmentant les précipitations totales, la hausse de la correction d’humidité de 10 % à 12 % dans la configuration standard de MAR a déjà sensiblement amélioré les hauteurs de neige simulées (biais passant de -5.1 cm à -4.4 cm, avec R restant à 0.86) (Tableau 3a). Avec le modèle ainsi déjà optimisé en températures et en précipitations, l’optimisation en enneigement a été fait en 2 étapes: i) en ajustant tout d’abord les températures seuils N/P contrôlant la partition entre neige et pluie, ce qui joue sur l’équivalent en eau liquide du manteau neigeux; ii) en ajustant ensuite la masse volumique de la neige fraîche contrôlant le profil de densité dans le manteau neigeux, ce qui joue sur la hauteur de neige correspondante. Faute de mesures de cet équivalent en eau dans la plupart des stations, c’est la hauteur de neige observée au sol qui a dû être utilisée pour évaluer la qualité de la simulation de ces 2 variables, ce qui introduit une incertitude supplémentaire difficile à estimer.

23Trois jeux de températures seuils ont été testés, en augmentant de 1 °C puis de 2 °C les températures seuils -1 °C/+1 °C de la configuration standard de MAR v3.13, tout en conservant la même valeur de 100 kg/m3 pour la masse volumique de la neige fraîche (Tableau 3b). Augmenter ces seuils fait augmenter significativement de -3.8 cm à +0.9 cm le biais moyen sur la hauteur de neige, sans impacter significativement les valeurs de R et RMSEc. Les meilleurs résultats sont obtenus pour le jeu 0°C/+2°C, qui i) minimise la valeur absolue du biais (-0.5 cm) et la RMSEc (5.5 cm) tout en maximisant la corrélation (R = 0.89) et ii) simule, toutes stations confondues, des hauteurs de neige en bon accord avec les observations - comme illustré sur la Figure 2a qui ne met en évidence aucun biais systématique en fonction de la hauteur de neige observée.

24En gardant ce jeu de seuils N/P ainsi ajusté, 2 autres masses volumiques de neige fraîche ont été testées: 50 kg/m³, et la variation entre 50 et 200 kg/m³ de la configuration standard (Tableau 3b). Une densité variable augmente la sous-estimation de -0.4 cm à -1.5 cm, alors que sa valeur réduite à 50 kg/m³ conduit à une surestimation de +0.9 cm. Comme le montre aussi la Figure 3, la hauteur de neige apparaît, dans les gammes testées, moins sensible à la densité initiale des couches de neige fraîche qu’aux températures seuils N/P. Les meilleurs résultats sont obtenus pour une masse volumique de 100 kg/m³.

25Apparaissant comme réalistes pour cette région et améliorant fortement la simulation de la hauteur de neige observée (Figure 2), ce sont ces valeurs de 0 °C/+2 °C et 100 kg/m3 qui ont été intégrées dans la configuration optimisée de MAR donnant la simulation de référence utilisée dans tout ce qui suit.

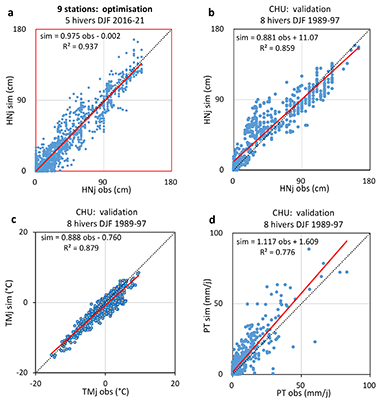
Figure 2. Comparaison entre valeurs journalières simulées et observées durant l’hiver (DJF). a : hauteur de neige HNj aux 9 stations nivologiques sur les 5 hivers 2016-21 d’optimisation. b, c, d : hauteur de neige HNj, température à 2 m TMj et précipitation PTj à la station X-L_CHU sur les 8 hivers 1989-97 de validation. En rouge : droite de régression (avec équation et R2). En pointillé noir : bissectrice.

a	configurations initiales
Hauteur de neige (cm) DJF :			Biais	RMSEc	R
configuration standard MAR v3.13 initiale :
humidité +10 %, N/P -1°/+1°, 50-200 kg/m3			-5.11	7.01	0.86
configuration standard avec humidité + 12 % :
humidité +12 %, N/P -1°/+1°, 50-200 kg/m3			-4.44	6.69	0.86
b	analyses de sensibilité
Hauteur de neige (cm) DJF :			Biais	RMSEc	R
Sensibilité aux températures seuils N/P :
humidité  +12 %, N/P -1°/+1°, 100 kg/m3			-3.79	6.52	0.86
humidité +12%, N/P  0°/+2°, 100 kg/m3			-0.49	5.49	0.89
humidité  +12 %, N/P +1°/+3°, 100 kg/m3			0.94	5.94	0.89
Sensibilité à la masse volumique de la neige fraîche :
humidité  +12 %, N/P 0°/+2°,   50 kg/m3			0.88	6.79	0.86
humidité +12%, N/P 0°/+2°, 100 kg/m3			-0.49	5.49	0.89
humidité  +12 %, N/P 0°/+2°, 50-200 kg/m3			-1.52	5.50	0.88
c	statistiques par station pour la simulation optimisée
	configuration: correction +12 %, N/P 0°/+2°, 100 kg/m3
	Hauteur de neige journalière (cm) DJF
Station	Moy	STD	Biais	RMSEc	R
X-L_LAC	11.30	14.98	-2.92	6.08	0.91
BRESS	10.28	15.62	0.18	6.56	0.91
X-L_CHU	49.76	45.51	2.47	12.34	0.96
MARKS	43.63	40.09	-3.08	13.12	0.95
MITTL	2.51	6.76	-0.09	4.88	0.74
BREIT	1.43	4.60	-1.29	3.79	0.75
COLM_M	0.21	1.74	0.18	0.87	0.98
BALE_M	0.35	1.83	0.05	1.01	0.87
STRAS_E	0.25	1.78	0.09	0.69	0.92
Moyenne	13.30	14.77	-0.49	5.49	0.89

Tableau 3. Optimisation de MAR (avec +12 % de correction d’humidité aux frontières) en hauteur de neige journalière sur les 9 stations nivologiques et les 5 hivers (DJF) 2016-21 : ajustement des paramètres de l’enneigement (températures seuils N/P, masse volumique de la neige fraîche). a : statistiques des simulations utilisant la configuration standard avec correction initiale (10 %) ou optimisée (12%). b : statistiques globales (9 stations) des analyses de sensibilité. c : statistiques par station pour la simulation optimisée de référence (12 %, 0 °C/+2 °C, 100 kg/m3). Critères statistiques : moyenne Moy et écart-type STD observés ; Biais moyen, écart quadratique moyen centré RMSEc, coefficient de corrélation R entre valeurs simulées et observées. En gras : simulation optimisée de référence.

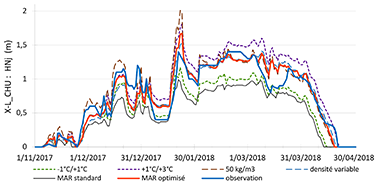
Figure 3. Hauteurs de neige journalières (HNj) simulées et observées à la station X-L_CHU (1220 m) sur l’hiver 2017-18 (Nov-Avr) d’optimisation. Simulation MAR standard initiale (humidité +10 %, températures seuils N/P -1°/+1°, masse volumique de la neige fraîche variable 50-200 kg/m3), simulation MAR optimisée de référence (humidité +12 %, températures seuils N/P 0°/+2°, masse volumique de la neige fraîche 100 kg/m3), simulations des tests de sensibilité aux seuils N/P et à la masse volumique de la neige fraîche.

C. Validation locale pour les 2 stations de référence

26Pour la station de montagne X-L_CHU, les critères statistiques de comparaison des températures, précipitations et hauteurs de neige hivernales (DJF) simulées et observées gardent pour les 8 hivers (DJF) 1989-97 de validation des valeurs proches de celles pour les 5 hivers (DJF) 2016-21 d’optimisation (Tableau 4). Ainsi, les biais passent de -0.7 °C à -1.1 °C, de 0.5 mm/j à 2.2 mm/j et de 2.5 cm à 6.3 cm, et les RMSEc de 1.8 °C à 1.5 °C, de 5.4 mm/j à 6.2 mm/j et de 12.3 cm à 15.8 cm. Les 3 droites de régression entre valeurs journalières simulées et observées sont très proches de la bissectrice, avec cependant une tendance de MAR à surestimer un peu les précipitations hivernales et à sous-estimer un peu les hauteurs de neige les plus élevées (Figure 2b,c,d). Tous les biais moyens et RMSEc sont largement inférieurs aux écarts-types STD observés. Ces résultats semblent donc acceptables et tout aussi satisfaisants que ceux de l’optimisation, malgré la différence de période. Une même qualité de performances est d’ailleurs obtenue tant pour une période hivernale Oct-Avr (plus réaliste pour les Hautes-Vosges) que pour l’année complète.

27Pour la station de plaine STRAS_E, où l’enneigement est négligeable, la validation a été faite sur les 62 hivers (DJF) 1960-2021, en considérant seulement les moyennes hivernales de température à 2 m et les précipitations totales hivernales (Tableau 4, Figure 4). Pour la température, les valeurs simulées et observées sont très bien corrélées (R = 0.98), et leurs droites de régression temporelle suggèrent une hausse simulée (+2.7 °C/62 hivers) un peu plus faible que la hausse observée (+3.1 °C/62 hivers). Pour les précipitations, la corrélation est de nouveau moins bonne (R = 0.84), et leurs droites de régression temporelle suggèrent, par rapport à la normale 1960-90, une hausse simulée (+21 %/62 hivers) qui est elle aussi un peu plus faible que la hausse observée (+27 %/62 hivers). Évaluées par les écarts-types des moyennes hivernales, les variabilités interannuelles simulée et observée sur la normale 1960-90 et sur la période 1960-2021 sont similaires tant pour la température moyenne (1.9 °C) que pour les cumuls de précipitation (37 mm/hiver). Ainsi, la légère sous-estimation par MAR de l’augmentation de la température et des précipitations hivernales depuis 1960 apparaît statistiquement non significative, ce qui la rend acceptable. Enfin, MAR simule très bien les températures hivernales, à un biais systématique de -0.6 °C près (Figure 4b), mais a tendance à sous-estimer un peu les précipitations observées avec une droite de régression (Figure 4c) suggérant que MAR sous-estime les hivers pluvieux et surestime plutôt les hivers secs.

28Ces bonnes performances valident ainsi localement, tant pour la montagne que pour la plaine, la configuration régionale optimisée de MAR, avec des résultats pluriannuels non seulement saisonniers mais aussi journaliers satisfaisants sur la période étudiée.

Station	a : X-L_CHU (1220m)						b : STRAS_E (150m)
hivers DJF	optimisation 2016-21			validation 1989-97			validation 1960-2021
	TMj	PTj	HNj	TMj	PTj	HNj	TM_hiv	PT_hiv
	(°C)	(mm/j)	(cm)	(°C)	(mm/j)	(cm)	(°C)	(mm/hiv)
Nombre	451	451	451	722	722	722	62	62
Moy_obs	-0.71	7.61	49.76	-1.11	5.29	40.07	2.49	111.67
STD_obs	4.35	12.29	45.51	4.24	10.15	42.00	1.87	36.54
Biais moyen	-0.75	0.52	2.47	-0.64	2.23	6.30	-0.63	-7.50
RMSEc	1.75	5.44	12.34	1.47	6.21	15.77	0.33	21.16
R	0.92	0.90	0.96	0.94	0.88	0.93	0.98	0.83

Tableau 4. Validation locale de la configuration optimisée de MAR sur les observations de 2 stations de référence pour les hivers DJF : (a) station X-L_CHU (1220 m) : sur les valeurs journalières des 8 hivers (DJF) 1989-97 (avec comparaison à la période d'optimisation 2016-21) ; (b) station STRAS_E Strasbourg-Entzheim : sur les valeurs hivernales (DJF) 1960-2021. Simulation de référence (correction d'humidité +12 %, N/P 0°C/+2°C, 100 kg/m3). Critères statistiques : moyenne Moy et écart-type STD des observations ; biais moyen, écart quadratique moyen centré RMSEc, coefficient de corrélation R entre valeurs simulées et observées.

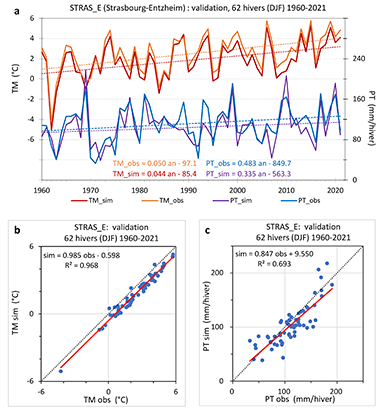
Figure 4. Comparaison des températures moyennes TM et précipitations totales PT hivernales (DJF) simulées (configuration optimisée de MAR) et observées à la station STRAS_E (Strasbourg-Entzheim) sur la période de validation 1960-2021 (62 hivers). a : évolution temporelle. b, c : diagrammes de dispersion simulation vs observation. En pointillé : droites de régression (avec équation et R2).

III. évolution 1960-2021 simulée

29Ainsi optimisé et validé localement en température, précipitation et hauteur de neige par rapport aux observations disponibles, le modèle MAR a permis de simuler, à l’échelle du domaine considéré, l’évolution climatique hivernale sur la période 1960-2021, et notamment celle de l’enneigement. Les variations absolues des variables simulées sur ces 62 hivers (DJF) ont été estimées d’après les droites de régression temporelles, et leurs variations relatives ont été exprimées en pourcentage de la normale climatique 1960-90 (30 hivers DJF). Le massif de la Forêt-Noire n’étant que très partiellement inclus dans le domaine considéré, tous les résultats mentionnés portent seulement sur les Vosges et la plaine rhénane. Mais la plupart des résultats vosgiens semblent bien pouvoir être extrapolés à la Forêt-Noire.

A. Température et flux énergétiques

30Pour la normale 1960-90, la température moyenne hivernale (DJF) simulée est fortement corrélée à l’altitude dans les Vosges, avec des valeurs restant négatives au-dessus de 800 m alors qu’elles peuvent dépasser +1.5 °C en moyenne en plaine du Rhin (Figure 5, gauche). MAR simule partout une hausse significative des températures depuis 1960, mais avec une augmentation qui est loin d’être uniforme: inférieure à +1.5 °C sur les sommets, mais jusqu’à plus de +3.0 °C en plaine (Figure 5, droite) où une hausse de +3.1 °C a été observée à la station de Strasbourg-Entzheim (Figure 4).

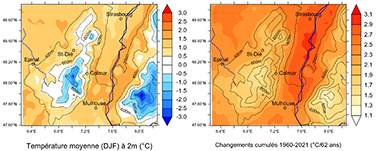
Figure 5. Évolution spatio-temporelle simulée des températures moyennes hivernales à 2 m pour les 62 hivers (DJF) 1960-2021. À gauche : normales hivernales (°C) sur la période de référence 1960-90. À droite : variations cumulées totales (°C/62 hivers) estimées d'après les droites de régression en chaque pixel.

31Cette augmentation de la température apparaît fortement corrélée avec l’augmentation relative simulée du flux infrarouge descendants (Figure 6, gauche) qui est minimale sur les crêtes (en particulier sur leur rebord alsacien) et maximale en plaine (supérieure à +3.5 % vers Colmar et même à +4.5 % vers Strasbourg).

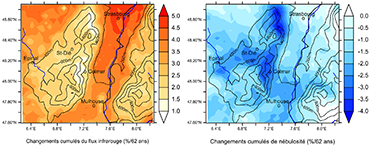
Figure 6. Variations cumulées simulées du flux infrarouge descendant (à gauche) et de la nébulosité totale (nuages bas, moyens et hauts) (à droite) pour les 62 hivers (DJF) 1960-2021. Variations estimées par les droites de régression en chaque pixel, en % de la normale 1960-90.

32MAR simule aussi partout une légère diminution (non significative statistiquement) de la nébulosité totale hivernale (Figure 6, droite): sa baisse relative est maximale sur le rebord alsacien de certaines crêtes (supérieure à 3.5 %) expliquant l’augmentation limitée du flux infrarouge descendant dans ces zones; elle est minimale en plaine du Rhin où elle diminue du Sud au Nord jusqu’à moins de 1.5 %. Ces résultats suggèrent ainsi que, durant les hivers (DJF), le rayonnement solaire absorbé par le sol à l’échelle du massif tend à augmenter à cause d’une moindre nébulosité (augmentant l’ensoleillement) et d’un moindre albédo sur une couverture neigeuse devenant moins étendue et/ou moins durable. Mais l’évolution du bilan énergétique, et notamment de l’énergie disponible en surface, est surtout affectée par l’augmentation hivernale du flux infrarouge descendant: son apport énergétique est en effet environ 10 fois supérieur à celui du rayonnement solaire absorbé par la surface en hiver.

33La comparaison entre les cartes de l’augmentation de température à 2 m simulée par MAR (Figure 5) et par les réanalyses ERA5 (Figure 7) montre la forte amélioration par MAR de la variabilité spatiale des champs simulés en surface, du fait d’une meilleure prise en compte de l’orographie grâce à sa résolution 4 km: dans les ERA5, les Vosges culminent à une altitude lissée de seulement 500 m. Ainsi, tout comme MAR, les ERA5 simulent une augmentation de la température hivernale plus importante en plaine rhénane que dans les massifs; mais avec un réchauffement en plaine moindre que pour MAR, dont la valeur est en meilleur accord avec celui observé (+3.1 °C à STRAS_E; voir Figure 4). Par ailleurs, les ERA5 simulent aussi un réchauffement d’environ 1.3-1.5 °C dans l’atmosphère libre à 850 hPa, ce qui correspond au réchauffement simulé par MAR pour les sommets des Vosges et de la Forêt-Noire qui culminent en hiver à une altitude de 870 hPa (Figure 7).

34Les champs de vent hivernaux (DJF) simulés par les ERA5 à 10 m et à 850 hPa ne montrent pas de changement significatif de la direction du vent dominant à ces 2 niveaux, mais seulement un renforcement depuis 1960 du vent dominant qui est du sud-ouest en surface et d’ouest en altitude (Figure 7). En moyenne sur le domaine (Figure 7), la composante zonale du vent à 850 hPa (resp. 700 hPa) a augmenté de +2.0 m/s (resp. +1.9 m/s) sur 62 ans, pour une vitesse zonale moyenne de 4.8 m/s (resp. 6 m/s) sur la normale 1960-90. La composante méridionale du vent, qui varie entre -et +1 m/s en moyenne, n’a quasiment pas changé depuis 1960. Il est toutefois important de mentionner que ces changements sur 62 ans sont de l’ordre de la variabilité interannuelle du vent moyen hivernal (DJF) et sont donc non significatifs statistiquement.

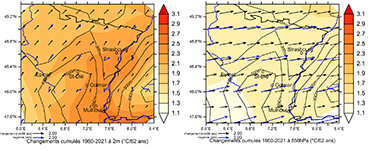
Figure 7. Variations de température et de vent simulées par les ERA5 en surface et dans l’atmosphère libre pour les 62 hivers (DJF) 1960-2021. Résolution spatiale : 0.3°x0.3° (soit environ 30 kmx30 km). À gauche : champs en surface (température à 2 m, vent à 10 m). À droite : champs à 850 hPa (~ 1500m). Pour chaque niveau : variations hivernales cumulées, estimées d’après les droites de régression par pixel, de la température (couleurs) et du vent (flèche noire). Les vitesses et directions du vent moyen sur la normale 1960-90 sont indiquées par les flèches bleues. Dans la légende, la longueur identique des flèches noire et bleue indique une vitesse de 2 m/s. Par rapport à la flèche bleue du vent normal, une diminution (resp. une augmentation) de la vitesse du vent est représentée par une flèche noire de direction opposée (resp. de même direction), à même direction du vent.

B. Précipitations

35Pour la normale 1960-90, les précipitations hivernales totales simulées apparaissent comme bien corrélées à l’altitude lissée, avec plus de 600 mm/hiver dans les Hautes-Vosges et jusqu’à moins de 50 mm/hiver en plaine (Figure 8a). Par rapport à cette normale, elles présentent depuis 1960 une augmentation relative, plus forte sur les Vosges (> 15 %) que dans la partie médiane de la plaine rhénane (< 15 %). Comme pour le vent à 850 et 700 hPa, l’augmentation de précipitation est non significative statistiquement car inférieure à la variabilité interannuelle.

36La partition simulée entre neige (Figure 8b) et pluie (Figure 8c) présente aussi une forte variabilité spatio-temporelle. Pour la normale 1960-90, la part neigeuse varie très fortement entre les Hautes-Vosges où la neige est largement majoritaire (jusqu’à plus de 450 mm/hiver) et la plaine rhénane où la pluie domine en hiver. À part dans les Hautes-Vosges où elles sont restées à peu près constantes, les précipitations neigeuses ont diminué partout au profit de la pluie, surtout dans la plaine peu arrosée. C’est donc l’augmentation partout significative de la pluie qui explique celle des précipitations totales. Ainsi, sur les Hautes-Vosges, l’augmentation simulée de plus de 15 % des précipitations totales se traduit par une hausse uniquement des pluies hivernales (de plus de 50 %) alors que les chutes de neige ont peu changé malgré la hausse des températures (Tableau 4).

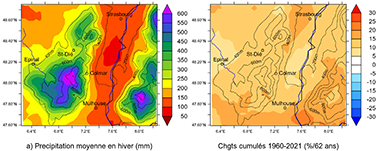
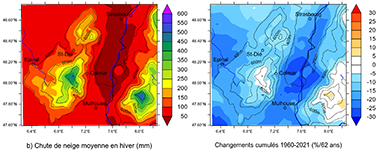
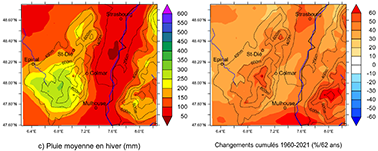
Figure 8. Évolution spatio-temporelle simulée des précipitations hivernales totales (a), neigeuses (b) et pluvieuses (c) pour les 62 hivers (DJF) 1960-2021. À gauche : normales 1960-90 (mm/hiver). À droite : variations cumulées (%/62 hivers) estimées d’après les droites de régression, en % de la normale 1960-90.

C. Enneigement

37Pour la normale 1960-90, l’enneigement moyen simulé est évidemment très contrasté, tant en hauteur de neige (Figure 9) qu’en nombre de jours enneigés (Figure 10), entre d’une part les Hautes-Vosges où le manteau neigeux est continu en hiver (DJF) et dépasse localement 70 cm en moyenne, et d’autre part la plaine peu et rarement enneigée. Cet enneigement a partout fortement diminué depuis 1960 mais, relativement à cette normale, bien davantage en plaine que dans les Hautes-Vosges où il a cependant déjà diminué de moitié : respectivement, jusqu’à plus de 70 % et seulement moins de 35 % de réduction pour la hauteur de neige, jusqu’à plus de 70 % et seulement moins de 20 % de réduction pour le nombre de jours enneigés.

38À 1000 m d’altitude dans les Vosges, la variabilité interannuelle est très élevée, mais les décennies 1990 et 2010 ont eu un enneigement moyen inférieur à celui des autres décennies de la période 1960-2021 (Figure 11). Globalement, l’enneigement moyen à 1000 m a diminué de moitié depuis 1960, passant de 40 cm à 20 cm en moyenne sur les 3 mois d’hiver.

39L’effet de l’altitude sur la variabilité simulée de l’enneigement apparaît bien en considérant 4 tranches d’altitude d’environ ±100 m autour de 500 m, 750 m, 1000 m et 1150 m (Tableau 5). À chaque tranche sont associées les moyennes des valeurs simulées pour tous les pixels présents dans cette tranche. Cet échantillonnage spatial peut bien sûr comporter un certain biais du fait des différences dans le nombre de pixels par tranche et dans les positions topographique et orographique des pixels d’une même tranche. Néanmoins l’effet de l’altitude sur les variations relatives depuis 1960 est manifeste : quand l’altitude décroît, la croissance de la température augmente, celle des précipitations pluvieuses diminue, et la décroissance des précipitations neigeuses et du nombre de jours enneigés augmente (Tableau 5).

40Il est important de noter que ces diminutions contrastées de l’enneigement simulées par MAR ne sont pas liées au choix d’une période hivernale limitée aux seuls 3 mois DJF, alors que l’enneigement dure généralement au moins de novembre à mars dans les Hautes-Vosges. Si on considère l’enneigement tous mois confondus, les mêmes tendances se retrouvent, avec même une amplification par rapport aux 3 mois DJF de l’hiver météorologique (Tableau 5). Enfin, une telle diminution significative de l’enneigement est aussi observée dans d’autres massifs comme les Alpes (Martin et Etchevers, 2005 ; Beaumet et al., 2021 ; Matiu et al., 2021) ou les Pyrénées (López-Moreno et al., 2020).

variation 1960-2021:		absolue	relative ( %/62 hivers), en % de la normale 1960-90
Altitude pixel (m)	Nb pixels	Température (°C/62hivers)	Précipitation neigeuse	Précipitation pluvieuse	Hauteur de neige	Nb Jours ³1cm neige
						DJF	Oct-Avr
[1100-1220] 1150	3	1.7	0	58	-47	-11	-25
[920-1100] 1000	16	1.7	-3	52	-50	-14	-31
[670-850] 750	56	1.9	-9	43	-59	-25	-41
[420-600] 500	153	2.1	-14	38	-71	-43	-54

Tableau 5. Variations simulées de la température à 2 m, des précipitations neigeuse et pluvieuse, de la hauteur de neige et du nombre de jours enneigés (≥ 1 cm) par tranche d’altitude dans les Vosges sur les 62 hivers (DJF) 1960-2021. Nombre de jours enneigés aussi pour les hivers complets (Oct-Avr). Variations estimées par droites de régression : absolue en température (°C) ; relative pour les autres, en % des normales 1960-90. Enfin, le nombre de pixels MAR par tranche d’altitude est listé.

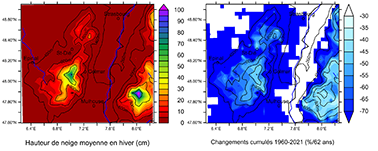
Figure 9. Évolution spatio-temporelle simulée de la hauteur de neige pour les 62 hivers (DJF) 1960-2021. À gauche: normales 1960-90 (cm/hiver). À droite: variations cumulées (%/62 hivers) estimées d’après les droites de régression par pixel, en % de la normale 1960-90. Pixels en blanc : hauteur de neige moyenne inférieure à 1 cm, et donc de variations relatives non significatives.

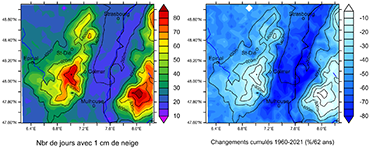
Figure 10. Évolution spatio-temporelle simulée du nombre de jours enneigés (≥ 1 cm) pour les 62 hivers (DJF) 1960-2021. À gauche : normales 1960-90 (cm/hiver). À droite : variations cumulées (%/62 hivers) estimées d’après les droites de régression par pixel, en % de la normale 1960-90.

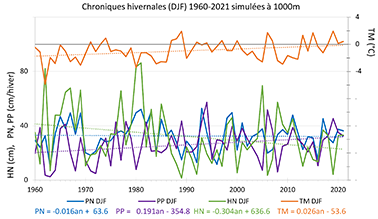
Figure 11. Évolution simulée des valeurs hivernales de la température moyenne à 2 m TM (°C), des précipitations neigeuses PN et pluvieuses PP (cm/3 mois) et de la hauteur de neige HN moyenne (cm) à 1000 m d’altitude sur les 62 hivers (DJF) 1960-2021. Ces valeurs sont les moyennes des valeurs des 16 pixels MAR de la tranche d’altitude 1000 m [920 m-1100 m]. En pointillé : droite de régression (avec équation).

IV. Discussion

41La hausse (significative statistiquement simulée par MAR des températures hivernales depuis 1960 s’est accompagnée, d’après les réanalyses ERA5, d’un renforcement (non significatif) de la circulation d’ouest en altitude et de sud-ouest en surface. Ceci explique l’augmentation (non significative) des précipitations totales (plus importantes sur la façade ouest des massifs des Vosges et de la Forêt Noire que sur la façade est); mais aussi le réchauffement (significatif) plus important en plaine rhénane à cause d’un effet de foehn renforcé: asséchant les masses d’air descendant des Vosges, il explique aussi la légère diminution de la nébulosité dans les zones de relief sous le vent dominant. En plaine, la fréquence des brouillards (considérés comme nuage bas dans MAR) n’a pas changé et brouille en quelque sorte le signal venant de la diminution de la nébulosité de moyenne et haute altitude.

42Ces résultats fournis par les simulations MAR contribuent à expliquer la diminution observée de l’enneigement depuis 1960, qui résulterait ainsi des changements non seulement dans la partition neige-pluie mais aussi dans la température au sol. Si la hauteur de neige simulée tend à diminuer (de moitié à 1000 m), ce n’est pas parce qu’il y a moins de précipitations (elles augmentent de plus de +16 % à 1000 m) ou qu’il neige moins qu’avant (peu de variation); c’est parce que les précipitations tombent maintenant davantage sous forme de pluie (accélérant la fonte de la neige), à cause de la hausse (+1.8 °C à 1000 m) des températures hivernales (DJF). Celle-ci contribue aussi à une fonte plus rapide du manteau neigeux fraîchement déposé. De ce fait, l’enneigement moyen s’avère corrélé tant aux précipitations neigeuses (R = +0.75) qu’à la température hivernale moyenne à 2 m (R = -0.66).

43L’augmentation simulée de l’énergie disponible pour la fonte de la neige au sol se vérifie en considérant les degrés-jour positifs cumulés sur l’hiver (DJF) - c’est-à-dire la somme sur l’hiver des seuls écarts positifs entre la température moyenne journalière à 2 m et le seuil de 0°C (Figure 12). Ce nombre de degrés-jour cumulés hivernaux est évidemment beaucoup plus élevé en plaine que dans le haut des massifs. Mais, par rapport à la normale 1960-90, son augmentation relative est maximale (jusqu’à plus de 70 %) sur les Hautes-Vosges malgré leur relativement faible réchauffement (+1.5-2 °C), tout en étant forte aussi dans le Nord de la plaine rhénane où le réchauffement dépasse +3 °C. Alors que le seuil de 0 °C était très rarement atteint pendant les hivers 1960-90, il est maintenant atteint presque 2 fois plus souvent, ce qui tend à réduire la durée de l’enneigement entre deux épisodes neigeux.

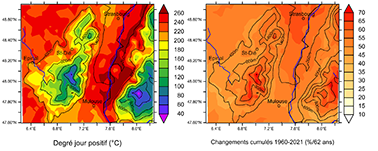
Figure 12. Évolution spatio-temporelle des nombres moyens de degrés-jour positifs cumulés sur les 62 hivers (DJF) 1960-2021. À gauche : normales (°C) 1960-90. À droite : changements cumulés (%/62 hivers) estimés d’après les droites de régression par pixel, en % de la normale 1960-90.

44La variabilité interannuelle des hauteurs de neige moyennes (DJF) simulées apparaît, à toutes les tranches d’altitude définies précédemment, comme corrélée à celle des anomalies de température moyenne hivernale (DJF) par rapport à la normale 1960-90 (Figure 13). Les droites de régression entre hauteur de neige et anomalie permettent d’estimer pour chacune de ces 4 tranches le réchauffement par rapport à cette normale qui serait nécessaire pour avoir en moyenne des hivers sans neige dans cette tranche. À 500 m et 750 m, il serait d’environ +2.7 °C et +2.9 °C, ce qui a déjà été observé par exemple pendant les hivers 1989-90, 2013-14 et 2019-20 qui ont été à peu près sans neige à ces altitudes. Il serait d’environ +3.8C à 1000 m (ce qui n’a encore jamais été observé) et +5 °C à 1150 m. Par ailleurs, les hivers les plus enneigés ont été les deux hivers les plus froids (1962-63, 1980-81) aux précipitations (neige et pluie) de respectivement 35 % et 1 % inférieures à la normale, mais aussi les 2 hivers 1966-67 et 1981-82 avec une anomalie de température proche de 0 °C mais des précipitations de 30-40 % supérieures à la normale. Cela montre que l’enneigement en altitude dépend non seulement de la température elle-même mais aussi des quantités de précipitation: quand l’altitude augmente (de 500 m à 1000 m puis à 1150 m), la corrélation de l’enneigement diminue (en valeur absolue) avec la température (-0.74, -0.65, -0.60 resp.) mais augmente avec les précipitations (0.15, 0.25, 0.31 resp.).

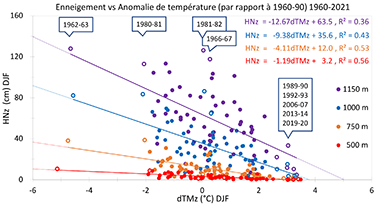
Figure 13. Dispersion interannuelle simulée de la hauteur de neige moyenne HNz (cm) vs l’anomalie de température dTMz (°C) par rapport à la normale 1960-90 pour 4 tranches d’altitude z (500 m, 750 m, 750 m, 1000 m) et les 62 hivers (DJF) 1960-2021. Droite de régression prolongée (avec équation) par tranche. Symbole "o" : hiver extrême (avec étiquette) cité dans le texte.

45Au vu de la dispersion autour de ces droites de régression, croissante avec l’altitude (en partie du fait des biais d’échantillonnage spatial évoqués plus haut et de la dépendance croissante aux quantités de précipitations hivernales vs la température avec l’altitude), ces premières estimations sont évidemment encore très incertaines, d’autant plus que la température influence aussi la partition pluie-neige des précipitations. Elles nécessiteraient donc d’être validées plus en profondeur, en réalisant par exemple des projections futures avec ce modèle MAR forcé par les scénarios futurs du GIEC, comme cela a déjà été fait pour la Belgique (Wyard et al., 2021).

Conclusion

46Ainsi, le modèle régional du climat MAR a pu être optimisé et validé sur les Vosges et la plaine d’Alsace, à l’aide d’observations journalières stationnelles de température, précipitation et hauteur de neige - moyennant un ajustement très limité mais réaliste de seulement 3 paramètres. Cette validation donne une certaine confiance dans l’estimation des tendances régionales simulées par MAR concernant l’évolution sur la période 1960-2021 de l’enneigement dans le massif des Vosges. Elles suggèrent une diminution (significative statistiquement) d’un facteur de 2 environ de l’enneigement, tant en hauteur de neige moyenne qu’en nombre de jours enneigés. Elles suggèrent aussi une légère augmentation (non significative) des précipitations totales hivernales suite à un renforcement (non significatif) de la circulation d’ouest, associée à une diminution relative des précipitations neigeuses, significative en dessous de 1000 m.

47Sur la base des tendances actuelles simulées, un réchauffement de 3.8 °C serait suffisant pour ne plus avoir de la neige en moyenne en dessous de 1000 m. Au-dessus de 1000 m, la diminution des chutes de neige n’est pas significative, ce qui suggère que seule l’augmentation (significative) d’environ +2 °C de la température explique cette diminution de l’enneigement. Dans les Hautes-Vosges, il ne neige pas moins qu’avant mais le seuil de 0 °C est de plus en plus souvent dépassé par les températures moyennes, faisant davantage fondre le manteau neigeux entre deux épisodes neigeux. Néanmoins, ces premières estimations et tendances simulées par MAR devront être validées à l’aide de projections futures réalisées avec la même configuration optimisée de MAR mais avec cette fois un forçage par des scénarios futurs du GIEC à la place des réanalyses ERA5 utilisées ici pour reconstruire le climat actuel observé.

48L’approche cartographique fine permise par MAR s’avère ainsi très utile pour caractériser les variabilités spatio-temporelles du climat et notamment de l’enneigement à l’échelle d’un massif et de son environnement.

Remerciements

49Les auteurs remercient Météo France pour la mise à disposition des données météorologiques nécessaires à cette étude. Concernant la station X-L_CHU du Chalet Universitaire du Chitelet à Xonrupt-Longemer, ils remercient P. M. David (observateur nivo-météorologue diplômé, alors gardien du chalet) qui a fourni ses propres données journalières 1989-97, ainsi que l’Association bénévole NIV’ose qu’il préside et l’Agence environnementale AtMO-Grand Est qui ont fourni, respectivement, les données journalières de hauteur de neige et de température de l’air pour les hivers 2016-21. Enfin, ils remercient les fournisseurs de données du projet ECA&D (https://www.ecad.eu/).

Bibliographie

50Ambroise, B., Perrin, J.L. & Reutenauer, D. (1995). Multicriterion validation of a semidistributed conceptual model of the water cycle in the Fecht catchment (Vosges massif, France). Water Resources Research, 31(6), 1467-1481.

51Amory, C., Kittel, C., Le Toumelin, L., Agosta, C., Delhasse, A., Favier, V. & Fettweis, X. (2021). Performance of MAR (v3.11) in simulating the drifting-snow climate and surface mass balance of Adélie Land, East Antarctica. Geosci. Model Dev., 14, 3487-3510. https://doi.org/10.5194/gmd-14-3487-2021

52Antwerpen, R. M., Tedesco, M., Fettweis, X., Alexander, P. & van de Berg, W. J. (2022). Assessing bare-ice albedo simulated by MAR over the Greenland ice sheet (2000-2021) and implications for meltwater production estimates. The Cryosphere, 16, 4185-4199. https://doi.org/10.5194/tc-16-4185-2022

53Beaumet, J., Ménégoz, M., Morin, S., Gallée, H., Fettweis, X., Six, D., Vincent, C., Wilhelm, B. & Anquetin, S. (2021). Twentieth century temperature and snow cover changes in the French Alps. Reg Environ Change, 21, 114. https://doi.org/10.1007/s10113-021-01830-x

54Damseaux, A., Fettweis, X., Lambert, M. & Cornet, Y. (2020). Representation of the rain shadow effect in Patagonia using an orographic-derived regional climate model. Int J Climatol., 40, 1769- 1783. https://doi.org/10.1002/joc.6300

55Delhasse, A., Kittel, C., Amory, C., Hofer, S., van As, D., S. Fausto, R. & Fettweis, X. (2020). Brief communication: Evaluation of the near-surface climate in ERA5 over the Greenland Ice Sheet. The Cryosphere, 14, 957-965. https://doi.org/10.5194/tc-14-957-2020

56De Ridder, K. & Gallée, H. (1998). Land surface-induced regional climate change in Southern Israel. J Appl Meteorol, 37, 1470-1485. https://doi.org/10.1175/1520-0450(1998)037<1470:LSIRCC>2.0.CO;2

57Duynkerke, P.G. & Driedonks, A.G.M. (1987). A model for the turbulent structure of the stratocumulus-topped atmospheric boundary layer. J Atmos Sci, 44, 43-64.

58Doutreloup, S., Wyard, C., Amory, C. & Fettweis, X. (2019). Sensitivity to Convective Schemes on Precipitation Simulated by the Regional Climate Model MAR over Belgium (1987-2017). Atmosphere, 10(1), 34. https://doi.org/10.3390/atmos10010034

59Fettweis, X. (2007). Reconstruction of the 1979-2006 Greenland ice sheet surface mass balance using the regional climate model MAR. The Cryosphere, 1, 21-40. https://doi.org/10.5194/tc-1-21-2007

60Fettweis, X., Hofer, S., Krebs-Kanzow, U., Amory, C., Aoki, T., Berends, C. J., Born, A., Box, J. E., Delhasse, A., Fujita, K., Gierz, P., Goelzer, H., Hanna, E., Hashimoto, A., Huybrechts, P., Kapsch, M.-L., King, M. D., Kittel, C., Lang, C., Langen, P. L., Lenaerts, J. T. M., Liston, G. E., Lohmann, G., Mernild, S. H., Mikolajewicz, U., Modali, K., Mottram, R. H., Niwano, M., Noël, B., Ryan, J. C., Smith, A., Streffing, J., Tedesco, M., van de Berg, W. J., van den Broeke, M., van de Wal, R. S. W., van Kampenhout, L., Wilton, D., Wouters, B., Ziemen, F. & Zolles, T. (2020). GrSMBMIP: intercomparison of the modelled 1980-2012 surface mass balance over the Greenland Ice Sheet. The Cryosphere, 14, 3935-3958. https://doi.org/10.5194/tc-14-3935-2020

61Gallee, H. & Schayes, G. (1994). Development of a three-dimensional meso-γ primitive equations model. Mon. Wea. Rev., 122, 671-685.

62Humbert, J. & Paul, P. (1982). La répartition spatiale des précipitations dans le bassin versant de la Petite Fecht à Soulzeren (Hautes Vosges). Premiers résultats. Recherches Géographiques à Strasbourg, 19-20-21, 93-104.

63Juillard, E. (1954). L’enneigement dans les Vosges et la plaine d’Alsace. Annales de l’Institut de Physique du Globe, Université de Strasbourg. Nouvelle série, Tome 7, 3e Partie Géophysique, 3-21.

64Klemes, V. (1986). Operational testing of hydrologic simulation models. Hydrological Sciences Journal, 31(1), 13-24.

65Klein Tank, A. M. G., Wijngaard, J. B., Können, G. P., Böhm, R., Demarée, G., Gocheva, A., Mileta, M., Pashiardis, S., Hejkrlik, L., Kern-Hansen, C., Heino, R., Bessemoulin, P., Müller-Westermeier, G., Tzanakou, M., Szalai, S., Pálsdóttir, T., Fitzgerald, D., Rubin, S., Capaldo, M., Maugeri, M., Leitass, A., Bukantis, A., Aberfeld, R., van Engelen, A. F. V., Forland, E., Mietus, M., Coelho, F., Mares, C., Razuvaev, V., Nieplova, E., Cegnar, T., Antonio López, J., Dahlström, B., Moberg, A., Kirchhofer, W., Ceylan, A., Pachaliuk, O., Alexander, L. V. & Petrovic, P. (2002). Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int. J. of Climatol., 22, 1441-1453.

66Lafaysse, M., Cluzet, B., Dumont, M., Lejeune, Y., Vionnet, V. & Morin, S. (2017). A multiphysical ensemble system of numerical snow modelling, The Cryosphere, 11, 1173-1198. https://doi.org/10.5194/tc-11-1173-2017

67López-Moreno, J.I., Soubeyroux, J.M., Gascoin, S., Alonso-Gonzalez, E., Durán-Gómez, N., Lafaysse, M., Vernay, M., Carmagnola, C. & Morin, S. (2020). Long-term trends (1958-2017) in snow cover duration and depth in the Pyrenees. Int J Climatol., 40, 6122-6136. https://doi.org/10.1002/joc.6571

68Martin, E. and Etchevers, P. (2005). Impact of climatic changes on snow cover and snow hydrology in the French Alps. Adv. Glob. Change Res., 23, 235-242. https://doi:10.1007/1-4020-3508-X 24

69Matiu, M., Crespi, A., Bertoldi, G., Carmagnola, C. M., Marty, C., Morin, S., Schöner, W., Cat Berro, D., Chiogna, G., De Gregorio, L., Kotlarski, S., Majone, B., Resch, G., Terzago, S., Valt, M., Beozzo, W., Cianfarra, P., Gouttevin, I., Marcolini, G., Notarnicola, C., Petitta, M., Scherrer, S. C., Strasser, U., Winkler, M., Zebisch, M., Cicogna, A., Cremonini, R., Debernardi, A., Faletto, M., Gaddo, M., Giovannini, L., Mercalli, L., Soubeyroux, J.-M., Sušnik, A., Trenti, A., Urbani, S. and Weilguni, V. (2021). Observed snow depth trends in the European Alps: 1971 to 2019. The Cryosphere, 15, 1343-1382. https://doi.org/10.5194/tc-15-1343-2021

70Paul, P. (1982). Le climat de la vallée de la Fecht - Aspects généraux. Recherches Géographiques à Strasbourg, 19-20-21, 65-78.

71Paul, P. (1984). Enneigement. In: Encyclopédie d’Alsace, Edition Publitotal, Strasbourg, vol.5, 2764-2765.

72Paul. P. & Roussel, I. (1985). Les précipitations exceptionnelles d’avril et mai 1983 à l’origine de fortes crues en Alsace et en Lorraine. Mosella, 15, 3-29.

73Wahl, L., Planchon, O. & David, P.M. (2009). Characteristics and seasonal evolution of firns and snow cornices in the High Vosges mountains (eastern France). Erdkunde, 63(1), 51-67.

74Wuest, C. (2021). Apport et validation du Modèle Atmosphérique Régional (MAR) en région Alsace-Vosges. Mémoire de Master en Sciences géographiques (option Climatologie). Département de Géographie, Faculté des Sciences, Université de Liège. 112 p.

75Wyard, C., Scholzen, C., Fettweis, X., Van Campenhout, J. & François, L. (2017). Decrease in climatic conditions favouring floods in the south-east of Belgium over 1959-2010 using the regional climate model MAR. Int. J. Climatol., 37, 2782-2796. https://doi.org/10.1002/joc.4879

76Wyard, C., Scholzen, C., Doutreloup, S., Hallot, É. & Fettweis, X. (2021). Future evolution of the hydroclimatic conditions favouring floods in the south-east of Belgium by 2100 using a regional climate model. Int J Climatol., 41, 647-662. https://doi.org/10.1002/joc.6642

ANNEXES

Annexe 1 : Description succincte du modèle MAR et de ses spécificités

77Le modèle hydrostatique MAR, dont la dernière version v3.13 a été complètement réécrite en Fortran 90, résout à 24 niveaux verticaux (de 2 m à 17 km au-dessus de la surface) l’évolution temporelle des température, vent, humidité et pression sur la base des équations de Navier–Stokes. Il résout aussi explicitement l’évolution des hydrométéores (particules de glace, neige, pluie, gouttes d’eau, glace et grêle) mais utilise des paramétrisations pour résoudre la turbulence (Duynkerke et Driedonks, 1987) et la convection (Doutreloup et al., 2019).

78Plutôt que de forcer la concentration des hydrométéores aux frontières latérales, MAR les génère progressivement à partir des autres variables forcées. Ce choix, qui permet de forcer MAR aussi par des modèles globaux ne fournissant pas ces champs, oblige cependant à considérer tout autour du domaine d’intérêt une zone de relaxation suffisamment grande (d’environ 20 pixels de large) pour permettre à MAR de générer ses propres nuages qui pourront alors éventuellement précipiter à l’intérieur du domaine. De plus, pour assurer la stabilité numérique de MAR, un filtrage numérique est assuré à chaque pas de temps et en chaque pixel par un lissage en fonction des 8 pixels voisins d’autant plus fort que la résolution spatiale est plus haute.

79La diffusion numérique créée par ce filtrage conduit à une certaine perte de masse de l’humidité aux frontières, qui doit alors être compensée. Du fait de différences entre les modèles tant en résolution spatiale (et donc en topographie lissée) que dans la formation de l’humidité saturante (qui peut être fortement différente à basses températures), une masse d’air peut arriver saturée en eau dans les champs de forçage (ici les ERA5) mais pas dans la physique du MAR lui-même. Pour ces 2 raisons, une correction relative de l’humidité spécifique de l’air aux frontières latérales a été imposée automatiquement dans MAR depuis la version v3.5 afin d’optimiser la comparaison aux observations lorsque MAR tourne à haute résolution (Wyard et al., 2017): +5 %, +7.5 % et +10 %, respectivement, pour des résolutions inférieures à 10 km, 7.5 km et 5 km.

80Pour simuler les processus de surface avec son module SISVAT (de Ridder et Gallée, 1998), chaque pixel MAR est composé de 3 sous-pixels représentant les 3 types d’occupation du sol (forêt de conifères, forêt de feuillus, ville, culture, prairie, sol nu, …) dominants sur ce pixel selon la base de données GLOCOVER v2.2 du projet Globcover 2005 de l’ESA (http://due.esrin.esa.int/page_globcover.php). Chaque type de sous-pixel a ses propres valeurs des paramètres contrôlant les processus de surface. SISVAT fait les calculs à chaque pas de temps pour chaque sous-pixel et transmet à MAR des moyennes par pixel pondérées en fonction de la couverture relative des 3 types d’occupation du sol. La conservation de la masse d’eau en chaque pixel est assurée depuis la version v3.12.

81Dans MAR, la pluie et la neige ne sont distinguées ni dans le schéma convectif (générant les pluies convectives), ni dans le schéma de turbulence (générant des précipitations par soulèvement orographique). Jusqu’à la version v3.11 (décrite en détail dans Amory et al., 2021), la partition neige-pluie (N/P) dans les précipitations totales au sol était fixée par le seuil de +0°C pour la température à 2 m - premier niveau atmosphérique simulé par MAR. Pour introduire plus de progressivité, une transition linéaire entre -1°C (100 % neige) et +1°C (100 % pluie) a été introduite dans la version v3.12 (décrite dans Antwerpen et al., 2022). La version v3.13 corrige un bug dans le schéma de nuage impactant la conversion de la neige en pluie qui était surestimée dans les versions précédentes.

82Basé sur le modèle CROCUS (Lafaysse et al., 2017), son sous-module "Neige" simule les processus et l’évolution des propriétés de la neige (densité, température, contenu en eau liquide, dendricité, taille des grains, sphéricité, …) dans le manteau neigeux, représenté dans MAR par au plus 15 couches d’épaisseur variable. Toute nouvelle couche de neige fraîche a une densité initiale fixée par paramètre, qui évolue ensuite en fonction des conditions atmosphériques et de son agrégation avec les couches sous-jacentes plus anciennes.

Annexe 2 : Données observées et simulées utilisées

83Les données journalières utilisées pour l’optimisation et la validation sont définies selon les normes horaires de l’OMM : pour la précipitation totale, cumul entre 06 hTU et 06 hTU + 24 h ; pour l’enneigement, hauteur de neige à 06 hTU ; pour la température moyenne journalière à 2 m, moyenne des températures simulées toutes les 30 s durant le jour [00-24[ à comparer à la moyenne des températures observées minimale (entre 18 hTU - 24h et 18 hTU) et maximale (entre 06 hTU et 06 hTU + 24 h) du jour. Pour chacune des stations, l’enneigement MAR retenu est l’enneigement maximal simulé pour les 1, 2 ou 3 sous-pixels à faible rugosité de surface (sol nu, prairie et/ou culture) présents dans le pixel MAR associé à la station.

84Pour la période d’optimisation 2016-21, les observations proviennent de 13 stations du réseau régional de Météo France ainsi que de la station X-L_CHU (1220 m) du Chalet Universitaire du Chitelet (Tableau 1). Pour X-L_CHU, l’enneigement a été mesuré par l’association NIV’ose, et la température par l’agence AtMO-Grand Est; faute de mesures locales durant cette période, ses précipitations ont été estimées par celles de la station X-L_Lac qui s’avèrent très semblables et bien corrélées (R = 0.91) sur la période 1991-1997.

85Pour la validation, les observations 1989-97 à la station XL-CHU proviennent des mesures de qualité alors faites par P. M. David (observateur nivo-météorologue) ; et les observations 1960-2021 à la station STRAS_E ont été extraites de la base de données ECA&D (Klein Tank et al., 2002).

86Pour la station X-L_CHU (1220 m), le pixel MAR correspondant se trouve être le plus élevé du maillage à 4 km de résolution. Son altitude a été artificiellement augmentée de 1095 m à 1220 m (+125 m), et celles des pixels voisins de +60 m pour éviter trop d’instabilités numériques locales dans MAR. Déjà testée par Wyard et al. (2017) pour évaluer la hauteur de neige mesurée au Mont-Rigi (660 m) en Belgique, une telle correction locale de la topographie permet aussi (i) de mieux simuler l’effet de barrière topographique des Vosges sur les précipitations, comme discuté dans Damseaux et al. (2020) pour la Patagonie en Argentine, et, faute d’une meilleure solution, (2) d’optimiser la comparaison avec les observations locales. Extrapoler vers le haut la hauteur de neige de pixels moins élevés sous-estime en effet l’enneigement lorsque seuls les hauts de versant sont enneigés, ce qui arrive fréquemment.

Pour citer cet article

A propos de : Xavier FETTWEIS

A propos de : Bruno AMBROISE

A propos de : Pierre-Marie DAVID

A propos de : Nicolas GHILAIN

A propos de : Patrice PAUL

A propos de : Cyril WUEST