- Portada
- Volume 17 (2013)
- numéro 3
- Non-linear height-diameter models for oriental beech (Fagus orientalis Lipsky) in the Hyrcanian forests, Iran
Vista(s): 0 (0 ULiège)
Descargar(s): 0 (0 ULiège)
Non-linear height-diameter models for oriental beech (Fagus orientalis Lipsky) in the Hyrcanian forests, Iran

Notes de la rédaction
Received on January 31, 2013; accepted on June 18, 2013
Résumé
Modèles non linéaires de diamètre de hauteur pour le hêtre oriental (Fagus orientalis Lipsky) dans les forêts Hyrcaniennes en Iran. La relation entre la hauteur des arbres et le diamètre est un élément important pour les modèles de croissance, de rendement, du budget de carbone et de volume du bois, et pour la description de la dynamique des peuplements. Six fonctions de croissance non linéaires (Chapman-Richards, Schnute, Lundqvist/Korf, Weibull, fonctions logistiques et exponentielles modifiées) ont été ajustées aux données de diamètre de hauteur des arbres de hêtre oriental dans les forêts mélangées hyrcaniennes d’Iran. La performance prévue des modèles a été évaluée à l’aide du R² ajusté (adj R²), de l’erreur quadratique moyenne (RMSE), du critère d’information d’Akaike (AIC), de la différence moyenne (MD), de la différence absolue moyenne (MAD) et de l’erreur quadratique moyenne (MS). Les résultats ont montré que chacun de ces six modèles représente environ 75 % de la variation totale de hauteur, mais produit différentes estimations asymptotiques. La performance prévue a également été évaluée à l’aide des validations croisées et par séparation des données en classes de 5 cm de diamètre à hauteur de poitrine (DBH) afin de calculer le MD pour chaque classe. Les visualisations de MD pour toutes les classes DBH ont montré que les six fonctions de croissance, sauf la logistique modifiée, produisent des erreurs de prédiction moyennes similaires pour les arbres de tailles petites et moyennes. Cependant, pour les arbres de grande taille, l’erreur de prédiction moyenne est plus élevée. La fonction de logistique modifiée est la moins performante, en raison d'un large biais. Les modèles exponentiels et de Lundqvist/Korf ont été rejetés en raison, respectivement, de leur comportement biologique illogique et des estimations déraisonnables pour les coefficients asymptotiques. En envisageant tous les critères mentionnés ci-dessus, les fonctions Chapman-Richards, Weibull et Schnute fournissent les prédictions de hauteur les plus satisfaisantes, mais la fonction de Chapman-Richards pourrait être recommandée pour une analyse plus approfondie en raison de sa meilleure performance.
Abstract
The relationship between tree height and diameter is an important element in growth and yield models, in carbon budget and timber volume models, and in the description of stand dynamics. Six non-linear growth functions (i.e. Chapman-Richards, Schnute, Lundqvist/Korf, Weibull, Modified Logistic and Exponential) were fitted to tree height-diameter data of oriental beech in the Hyrcanian mixed hardwood forests of Iran. The predictive performance of these models was in the first place assessed by means of different model evaluation criteria such as adjusted R squared (adj R2), root mean square error (RMSE), Akaike information criterion (AIC), mean difference (MD), mean absolute difference (MAD) and mean square (MS) error criteria. Although each of the six models accounted for approximately 75% of total variation in height, a large difference in asymptotic estimates was observed. Apart from this, the predictive performance of the models was also evaluated by means of cross-validation and by splitting the data into 5-cm diameter classes. Plotting the MD in relation to these diameter at breast height (DBH) classes showed for all growth functions, except for the Modified Logistic function, similar mean prediction errors for small- and medium-sized trees. Large-sized trees, however, showed a higher mean prediction error. The Modified Logistic function showed the worst performance due to a large model bias. The Exponential and Lundqvist/Korf models were discarded due to their showing biologically illogical behavior and unreasonable estimates for the asymptotic coefficient, respectively. Considering all the above-mentioned criteria, the Chapman-Richards, Weibull, and Schnute functions provided the most satisfactory height predictions. However, we would recommend the Chapman-Richards function for further analysis because of its higher predictive performance.
Tabla de contenidos
1. Introduction
1Covering an area of approximately 1.85 million ha, the Hyrcanian forests account for approximately 15% of Iranian forests and 1.1% of the country’s total area. These forests range from sea level up to an elevation of 2,800 m and comprise various forest types including no less than 80 woody species (trees and shrubs). Oriental beech (Fagus orientalis Lipsky), oak (Quercus castaneifolia Coss. ex J.Gay), maple (Acer velutinum Boiss.), hornbeam (Carpinus betulus L.) and alder (Alnus subcordata C.A.Mey.) are among the main tree species in these forests. The Hyrcanian forests have been forestland since the third geological era and are considered to be one of the oldest forests in the world (Sagheb-Talebi et al., 2004).
2The relationship between tree height and diameter at breast height (DBH) is one of the most important components of forest structure. Estimations of timber volume, site index, succession, carbon sequestration (Spurr, 1952; Botkin et al., 1972; Kurz et al., 1992; Vanclay, 1994; Peng et al., 2001), as well as stand description and damage appraisals (Parresol, 1992; Zhang, 1997) are highly related to the tree height-DBH relationship. Being one of the most commonly measured parameters in forest inventories, DBH is easily measured with little investment of time and cost and with a high level of accuracy. By contrast, the necessary investment of time, the chance of observer error and the occurrence of visual obstacles are among the main difficulties in measuring tree height (Colbert et al., 2002; Krisnawati et al., 2010). Therefore, in most forest inventories, the heights of only a few trees in a sample plot are measured, whereas the DBHs of all trees are measured. Consequently, height-DBH equations are very useful for the prediction of missing and unmeasured tree heights from field measurements and for numerous forest growth simulators (Huang et al., 2000; Peng et al., 2001; Lumbres et al., 2011). Furthermore, vertical forest structure can be well analyzed using height-DBH equations (e.g., Wykoff et al., 1982; Van Deusen et al., 1985; Larsen et al., 1987; Ritchie et al., 1986; Larsen, 1994, Colbert et al., 2002).
3A wide variety of models have been proposed for height-diameter relationships for different species and different forest regions. As Krisnawati et al. (2010) state, the approaches used for modeling height-diameter vary from linear to non-linear models. Curtis (1967) compared thirteen height-diameter models using linear regression techniques. On the other hand, Huang et al. (1992) selected the most appropriate height-diameter functions for major tree species out of 20 weighted non-linear techniques. These authors observed that the Weibull, the Modified Logistic, the Chapman-Richards and the Schnute functions generally provided the most satisfactory results. Zhang (1997) cross-validated six non-linear growth functions fitted to the tree height-diameter data of ten conifer species collected in the inland northwest of the United States. He concluded that the Schnute, Weibull, and Chapman-Richards functions presented the best predictive performance. Fang et al. (1998) investigated 33 height-diameter equations for tropical forests on Hainan Island in southern China. Peng et al. (2001) fitted six commonly used non-linear growth models to the tree height-diameter data of nine major tree species in Ontario's boreal forests. The results showed that the Chapman-Richards, Weibull, and Schnute functions provided the most satisfactory height predictions based on predictive performance criteria. Sánchez et al. (2003) used 26 linear and non-linear height-diameter functions for Pinus radiata D.Don throughout Galicia in the northwest of Spain and found that the Tomé model (Tomé, 1989) resulted in the best height estimates. Lumbres et al. (2011) developed and validated height diameter models for the three Pinus and one Larix species in South Korea using the six widely used non-linear growth functions. They showed that the Modified Logistic and Lundqvist/Korf models performed best compared to the other models based on a rank analysis. Pormajidian (1992) and Siahipour et al. (2002) have recommended non-linear models of height-diameter for Picea abies (L.) H.Karst. afforestation in Kelardasht region and Guilan province (in the north of Iran). In order to determine the most appropriate relationship between the diameter and height of Picea abies in Kelardasht afforestation (in the north of Iran), Fallah (2009) fitted 17 non-linear models to these data and selected the most satisfactory model based on MS error and R2.
4One of the most abundant and economic valuable hardwood genera in Hyrcanian forests is the Fagus genus. Beech forests account for approximately 17.6% of the total forest area, 30% of the standing volume and 23.6% of the stem number in the Hyrcanian forests in Iran. The average beech volume per ha varies between 480 and 740 cubic meters in pure stands and 600 and 700 cubic meters in mixed stands (Sagheb-Talebi et al., 2004). Because of the importance of oriental beech (Fagus orientalis) as one of the main timber species of the Hyrcanian forests, the aim of this study was to fit six commonly used non-linear growth models to height-diameter data of beech collected in the Tarbiat Modares University forest and to select the best model based on different evaluation criteria.
2. Materials and methods
2.1. Study site
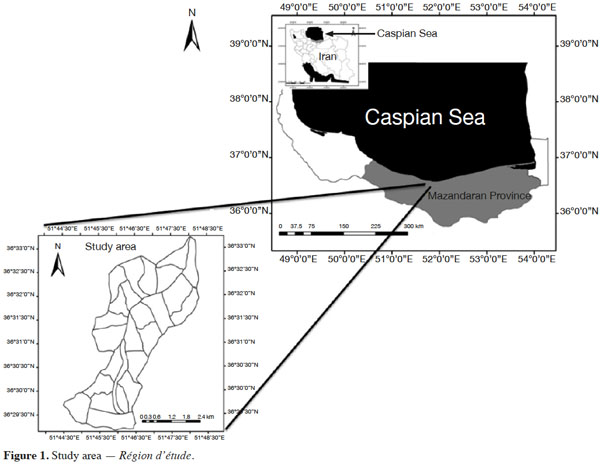
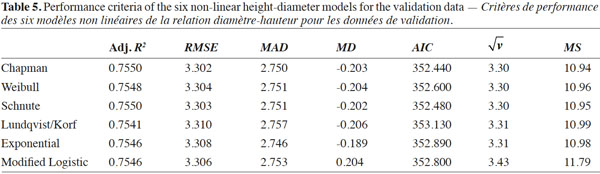
5This research was conducted in the Tarbiat Modares University (TMU) forest, a temperate forest forming part of the Hyrcanian Forests, located in the Mazandaran province in the north of Iran, between 36° 31' 56" N and 36° 32' 11" N latitudes and 51° 47' 49" E and 51 ° 47' 56" E longitudes (Figure 1). The study area is approximately 300 ha and its elevation varies from 1,000 m to 1,500 m above sea level. The minimum temperature in December is 6.6 °C, and the highest temperature, 25 °C, occurs in June. The mean annual precipitation of the study area is approximately 1,500 mm, measured at the Nowshahr city meteorological station, which is located 40 km away from the study area. The study area consists of mixed and uneven-aged forests, dominated by Fagus orientalis associated with Carpinus betulus, Acer velutinum, Parrotia persica C.A.Mey., Sorbus torminalis (L.) Crantz, Quercus castaneifolia, Alnus subcordata, Acer laetum C.A.Mey., Prunus avium (L.) L., Ulmus glabra Huds. and Tilia begoniifolia Steven species. The forest is managed following close-to-nature principles with single selection harvesting techniques. The bedrock is mainly limestone-dolomite with a silty-clay-loam soil texture (Kooch et al., 2010).
2.2. Data, models and methods
6The data used for modeling the height-DBH relationships were collected in 2012 using a random- systematic network of temporary sample plots. The interval between the grid lines was set at 200 and 100 m longitude and latitude, respectively. Two grid lines out of six were selected after field inspection. A total of 43 gridline intersections coinciding with plot centers were located in the field by GPS (Garmin 76 CSX) navigation. Plots with no evidence of disturbance including forest harvesting were discarded. These plots were circular-shaped and 0.1 ha in size. The plots extended the altitudinal belt ranging from 1,000 to 1,500 m a.s.l.
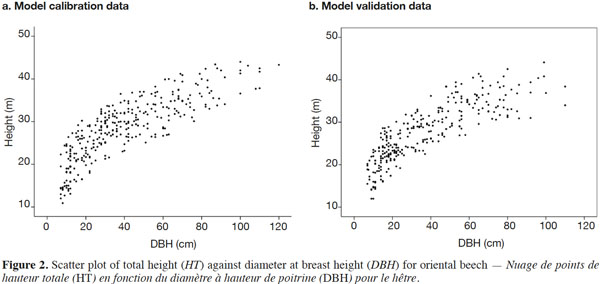
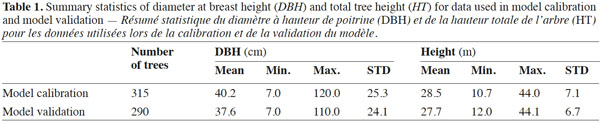
7All trees with a DBH > 7 cm within the plots were measured for diameter at breast height (DBH) using a caliper to the nearest millimeter and the total height of all beech trees was measured using a Vertex IV height meter. Multi-stemmed and damaged-top trees were not included in the analysis. A total of 605 individual height-diameter measurements for beech trees were recorded in the study area. The available tree height-diameter data were separated into two sets based on the grids: grid line 1 (n = 315) and grid line 2 (n = 290) were used for model calibration and model validation, respectively. Both datasets covered approximately the same ranges of DBH and height (Figure 2). Summary statistics for these two datasets are provided in table 1.
8A wide variety of non-linear models are often recommended for modeling the relationships between tree height and DBH (for example, Huang et al., 1992; Moore et al., 1996; Zhang, 1997; Fang et al., 1998; Fekedulegn et al., 1999; Peng, 1999; Peng et al., 2001). Based on these studies, six non-linear growth functions (Table 2) were selected as candidate height-diameter models. These six non-linear growth functions have been widely used in the literature due to their appropriate mathematical properties and promising predictive performances for tree height-diameter relationships (Brewer et al., 1985; Arabatzis et al., 1992; Huang et al., 1992; Zeide, 1993; Zhang et al., 1996; Zhang, 1997; Fang et al., 1998; Fekedulegn et al., 1999; Huang, 1999). All of these six non-linear models present an asymptotic behavior (parameter a in the models) in terms of the maximum tree height.

9The NLIN procedure in the Statistical Analysis System (SAS Institute Inc., 2002) was used to fit the six candidate models (Table 2) from the calibration dataset. This procedure applies an iterative process depending on the starting values for the parameters of the model being provided. The Gauss-Newton, the Marquardt, and the steepest descent methods are the three main iterative methods in the NLIN procedure. When parameter estimates of the model are highly correlated, the Marquardt method is considered to be the most useful (Fang et al., 1998). This method was therefore used in this study. Multiple initial values for the model parameters were used to guarantee that the least-squares solution was global rather than local. The homogeneity of variance assumption was investigated by plotting studentized residuals against the predicted height. This plot showed no significant evidence of unequal error variances; therefore, ordinary non-linear least-squares instead of weighted least-squares were used for parameter estimation. The data used for modeling height-diameter relationships often contained measurements of height and DBH from multiple trees from the same sample plot. These groups of height-diameter measurements may violate the basic assumption of independence, as multiple observations from a single sampling unit may be highly correlated (Sharma et al., 2007). The Durbin-Watson (DW) test carried out in SigmaPlot version 12.0 (Systat Software, Inc., San Jose California USA, www.sigmaplot.comfor), was used to check the autocorrelation in non-linear models. For all of the six models, DW statistics were greater than 2, showing that there was no autocorrelation. This means that there was no violation of the independence assumption.
2.3. Model performance criteria
10The selection of appropriate criteria to assess the model performance is a critical consideration. There is no single criterion for selecting the best regression model from among a number of models (Draper et al., 1998; Aertsen et al., 2010). Using multiple measurements of performance instead of single measurements is a common and more objective approach (Dawson et al., 2007; Aertsen et al., 2010). In the present study, various criteria were chosen and applied to evaluate the predictive performance of the models. In the following equations,
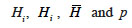
11stand respectively for observed value, fitted value, mean of the observed values and number of parameters used in the model.
12The most commonly used criteria to evaluate the model performance are the coefficient of determination (R2) (Pearson, 1896) and its modification (adjusted coefficient of determination). They are estimated as:
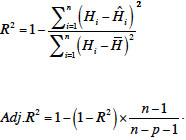
13The root mean square error (RMSE) is a well-accepted goodness-of-fit indicator describing the difference in observed and predicted values in the appropriate units (Harmel et al., 2007; Aertsen et al., 2010). RMSE is defined as follows (Aertsen et al., 2010):
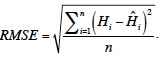
14The Akaike Information Criterion (AIC) is considered as one of the most reliable criteria for comparing models with a range of parameters (Burnham et al., 2002; Sharma, 2009). The model with the smallest AIC is considered optimal. For the least squares fit, it is calculated as follows (Dawson et al., 2007; Aertsen et al., 2010):
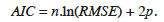
15The difference between the observed and the fitted tree heights is considered as the prediction error. The mean difference (MD) and mean absolute difference (MAD) are computed as follows:
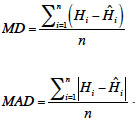
16
17Average underestimation and overestimation are indicated by positive and negative MD values, respectively. Mean square (MS) error is also considered as the indication of the model's precision. According to Zhang (1997) it is calculated as:
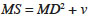
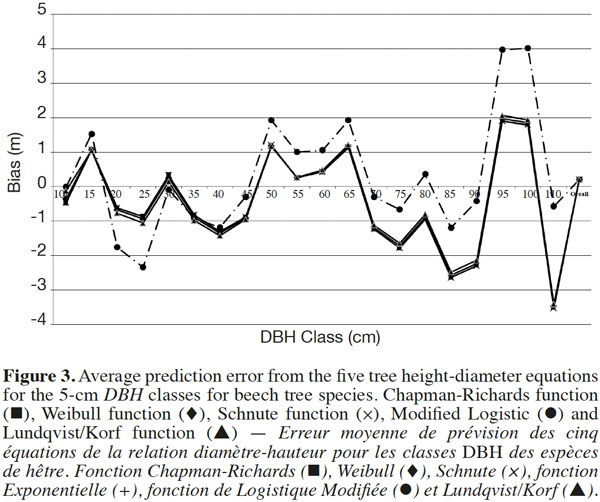
18where MD is the mean difference and v is the variance of the prediction errors. In addition to using the above-mentioned criteria, all curves generated with the different models were also checked with respect to their biological realism (Sharma, 2009). As the final step, in order to select the best model, the model validation dataset was divided into 5-cm DBH classes (7.5-12.5 cm, 12.6-17.5 cm, etc.) and the adequacy of the six models was evaluated on this basis. The mean prediction error computed for each DBH class using each of the six height-diameter models was plotted against the corresponding DBH class (Figure 3).
3. Results
3.1. Model calibration
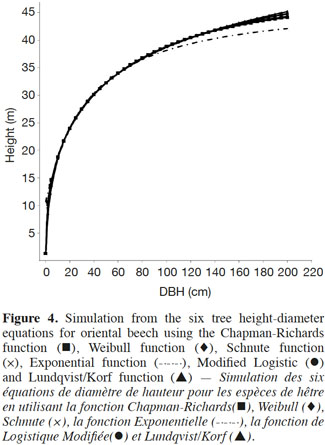
19The results of the six non-linear height growth functions for oriental beech are presented in table 3. The coefficients of all the models were statistically significant at a = 0.05. Table 4 shows the measures of performance for all six non-linear growth functions modeled in this study. Models with the lowest RMSE and AIC values and the R² and adjusted R² closest to unity are known to perform best (Aertsen et al., 2010). The adjusted R2 values indicate that all models produced nearly identical fits explaining approximately 75% of the total variation in height. The differences in the R2 values between the models were negligible. The MDs ranged from 0.001 to 0.006 whereas the MADs ranged from 2.894 to 2.908. In general, mean prediction errors were small for all six growth functions. Referring to table 4, it is evident that the differences between the model performance criteria were very small. Plotting the model residuals against the fitted values showed for all the models a random distribution of the residuals. Asymptote coefficients of the six growth functions (coefficient a in table 3), on the other hand, showed a significant difference. The Chapman-Richards, Schnute and Exponential models showed similar asymptotic coefficients. The asymptotic coefficient of the Lundqvist/Korf function was the highest compared to the five other functions. This value was approximately twice as large as the asymptotic coefficients of the other models (except for the Modified Logistic model).
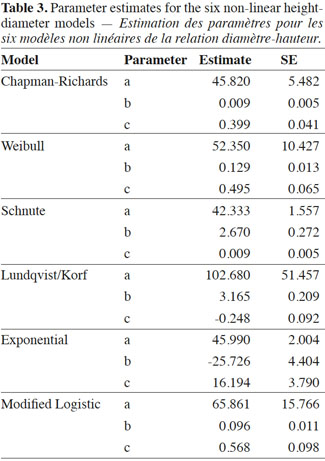
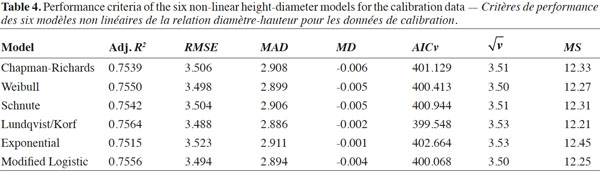
20The prediction performance of all the models was investigated with tree diameters ranging from 0 to 200 cm. Figure 4 shows the curved shapes of all six height growth models for oriental beech. For small- and medium-sized trees (e.g. DBH < 100 cm), the six growth functions showed similar predictions of tree height. For very small sized trees (DBH < 10 cm), the Exponential model predicted at zero DBH a height of approximately 11 m, which was much greater than the expected 1.3 m. For large-sized trees, the Lundqvist/Korf model in turn predicted remarkably greater tree heights, followed by the Modified Logistic function. The tree height estimations using the Chapman-Richards, Weibull, and Schnute functions were very similar. The Exponential function produced the smallest predictions for large-sized trees (Figure 4). It would be possible to confirm these results by adding a smooth line to the residual versus fitted graph, as this would help to show the trend. A residual distribution of the Exponential function showed a slight trend towards higher positive residuals with an increased response value. The curves extracted from the Richards, Weibull, Schnute, Modified Logistic and Lundqvist/Korf functions were very similar, but the asymptotic coefficient resulting from the Lundqvist/Korf gave an unreasonable value for beech in the study area.
3.2. Model validation
21The values of Adj R2, RMSE, AIC, MD, MAD, √v and MS are presented in table 5 for each model based on the validation dataset. Referring to this table, it is clear that the Chapman-Richards model performed slightly better than the other models. The overall mean prediction errors ranged from 0.189 to 0.206 m depending on the model. The Lundqvist/Korf model had the highest MD value, but the differences between all the models were negligible. As mentioned above, the model validation dataset was divided into 5-cm DBH classes and the MD for each DBH class was calculated for each of the non-linear models. The MD for each DBH class was plotted against its corresponding DBH class (Figure 3) in order to select the best model. For small- and medium-sized trees, this plot showed similar mean prediction errors for all six growth functions, except for the Modified Logistic model. For the large-sized trees, on the other hand, all models showed higher mean prediction errors.
4. Discussion
22It is apparent from the model statistics that each growth function was equally fitted to the tree height-diameter data. The models accounted for approximately 75% of the total variation in height. This is consistent with the findings reported by Huang et al., 1992; Zhang, 1997; Peng et al., 2001 and Krisnawati et al., 2010. These authors also observed similar fits for all six functions. The models developed in this study explained a relatively high proportion of the total variation in observed tree height, although in some other studies (e.g. Zhang et al., 1996; Colbert et al., 2002; Leduc et al., 2009; Sharma, 2009; Lumbres et al., 2011) the total explained variation was much higher by comparison. In order to select the best model, several features need to be considered. We found that the predicted height at zero DBH with the Exponential model was much greater than the theoretical 1.3 m. Some researchers state that biological logics are also important and should always be considered (e.g. Vanclay et al., 1997; Ratkowsky, 1990; Schabenberger et al., 2002; Sharma, 2009). Therefore, the Exponential model was excluded from further analysis here. Plotting the MD for each DBH class against its corresponding DBH showed that the Modified Logistic was the worst model based on this evaluation criterion, and thus this model could also be discarded from further analysis. The Lundqvist/Korf model, on the other hand, had the highest estimates for the asymptotic value, which was also unreasonably high. This feature of the Lundqvist/Korf function has also been observed in other studies on tree height and DBH modeling (Zeide, 1989; Moore et al., 1996; Zhang, 1997; Peng et al., 2001; Krisnawati et al., 2010). According to Zhang (1997), the asymptotic coefficient parameter has the lowest stability in non-linear growth function modeling. Therefore, biologically unreasonable upper asymptotes may be computed by fitting these growth functions using the least squares method, especially when few data observations exist near the asymptote. Care should therefore be taken in extrapolating the models beyond the calibration data range, because overprediction or underprediction may occur for large-sized trees. To overcome this problem, some researchers have constrained the growth functions by fixing the asymptote at a constant value such as a champion big tree and estimating all other parameters in the models (e.g. Shifley et al., 1984; Brewer et al., 1985; Zhang, 1997). However, a champion big tree was not available in this study for oriental beech. The Chapman-Richards, Weibull, and Schnute functions all showed superior prediction performance in terms of mathematical features, biological interpretation of parameters and accurate prediction. Nevertheless, we recommend the Chapman-Richards model for this study area because of its slightly better predictive performance. Our results are consistent with findings reported by Zhang (1997) and Peng et al. (2001). In general, the Chapman-Richards model should be considered as the best model for modeling height growth of oriental beech throughout the study region. Since the height-diameter relationship in a forest varies due to the variability in site and stand conditions, a single height-diameter relationship may not be appropriate for estimating all the possible relationships that may be found within a forest (Krisnawati et al., 2010). There are two possible alternative approaches for estimating tree height. The first is to develop a height-diameter model separately for each stand and the second is to use generalized height-diameter models in which variability in site and stand conditions is considered by including additional stand variables as well as tree diameter (e.g. Bi et al., 2000; Staudhammer et al., 2000; Sánchez et al., 2003; Sharma et al., 2004; Krisnawati et al., 2010). The first approach is, however, time-consuming and costly, whereas the second is practical and could provide more accurate height estimates.
Bibliographie
Aertsen W. et al., 2010. Comparison and ranking of different modeling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model., 221, 1119-1130.
Arabatzis A.A. & Burkhart H.E., 1992. An evaluation of sampling methods and model forms for estimating height-diameter relationships in loblolly pine plantations. For. Sci., 38, 192-198.
Bi H., Jurskis V. & O’Gara J., 2000. Improving height prediction of regrowth eucalypts by incorporating the mean size of site trees in a modified Chapman-Richards equation. Aust. For., 63, 255-264.
Botkin D.B., Jamak J.F. & Wallis J.R., 1972. Some ecological consequences of a computer model of forest growth. J. Ecol., 60, 849-873.
Brewer J.A., Burns P.Y. & Cao Q.V., 1985. Short-term projection accuracy of five asymptotic height-age curves for loblolly pine. For. Sci., 31, 414-418.
Burnham K.P. & Anderson D.R., 2002. Model selection and inference. A practical information-theoretic approach. New York, USA: Springer-Verlag.
Chapman D.G., 1961. Statistical problems in dynamics of exploited fisheries populations. In: Neyman J., ed. Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, June 20-July 30, 1960, Statistical Laboratory of the University of California, Berkeley. Berkeley, CA, USA: University of California Press, Vol. 4, 153-168.
Colbert K.C., Larsen D.R. & Lootens J.R., 2002. Height-diameter equations for thirteen Midwestern bottomland hardwood species. Nor. J. Appl. For., 19, 171-176.
Curtis R.O., 1967. Height-diameter and height-diameter-age equations for second-growth Douglas fir. For. Sci., 13, 365-375.
Dawson C.W., Abrahart R.J. & See L.M., 2007. Hydrotest: a web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Modell. Softw., 22, 1034-1052.
Draper N. & Smith H., 1998. Applied regression analysis. 3rd ed. London: John Wiley and Sons Inc.
Fallah A., 2009. Determination of the best diameter-height model for the Norway spruce (Picea abies [L.] H.Karst.) in Kelardasht afforestation (North of Iran). J. Appl. Sci., 9, 3870-3875.
Fang Z.X. & Bailey R.L., 1998. Height-diameter models for tropical forests on Hainan Island in southern China. For. Ecol. Manage., 110, 315-327.
Fekedulegn D., Siurtain M., Padraig M. & Colbert J., 1999. Parameter estimation of nonlinear growth models in forestry. Silva Fennica, 33, 327-336.
Harmel R.D. & Smith P.K., 2007. Consideration of measurement uncertainty in the evaluation of goodness-of-fit in hydrologic and water quality modeling. J. Hydrol., 337, 326-336.
Huang S., 1999. Ecoregion-based individual tree height-diameter models for lodgepole pine in Alberta. West. J. Appl. For., 14, 186-193.
Huang S., Titus S.J. & Wiens D.P., 1992. Comparison of nonlinear height-diameter functions for major Alberta tree species. Can. J. For. Res., 22, 1297-1304.
Huang S., Price D. & Titus S.J., 2000. Development of ecoregion-based height-diameter models for white spruce in boreal forests. For. Ecol. Manage., 129, 125-141.
Kooch Y., Hosseini S.M., Mohammadi J. & Hojjati S.M., 2010. The effects of gap disturbance on soil chemical and biochemical properties in a mixed beech – hornbeam forest of Iran. Ecol. Balkanica, 2, 39-56.
Krisnawati H., Wang Y. & Ades P.K., 2010. Generalized height-diameter model for Acacia mangium Willd. plantations in South Sumatra. J. For. Res., 7, 1-19.
Kurz W.A., Apps M.J., Webb T.M. & McNamee P.J., 1992. The carbon budget of the Canadian forest sector: phase 1. Information Report NOR-X-326. Edmonton, AB, Canada: Forestry Canada, Northwest Region, Northern Forestry Centre.
Larsen D.R., 1994. Adaptable stand dynamics model integrating site-specific growth for innovative silvicultural prescriptions. For. Ecol. Manage., 69, 245-257.
Larsen D.R. & Hann D.W., 1987. Height-diameter equations for seventeen tree species in southwest Oregon. Research note 49. Corvallis, OR, USA: Oregon State University, Forest Research Laboratory.
Leduc D. & Goelz J., 2009. A height-diameter curve for longleaf pine plantations in the Gulf Coastal plain. South. J. Appl. For., 33, 164-170.
Lumbres I.R.C. et al., 2011. Development and validation of nonlinear height–DBH models for major coniferous tree species in Korea. For. Sci. Technol., 7, 117-125.
Moore J.A., Zhang L. & Stuck D., 1996. Height-diameter equations for ten tree species in the Inland Northwest. West. J. Appl. For., 11, 132-137.
Parresol B.R., 1992. Bald cypress height-diameter equations and their prediction confidence intervals. Can. J. For. Res., 22, 1429-1434.
Pearson K., 1896. Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia. Philos. Trans. R. Soc. London, 187, 253-318.
Peng C.H., 1999. Nonlinear height-diameter models for nine tree species in Ontario boreal forests. Forest Research Report. Sault Ste Marie, ON, Canada: Forest Research Institute.
Peng C., Zhang L. & Liu J., 2001. Developing and validating nonlinear height-diameter models for major tree species of Ontario’s boreal forests. North. J. Appl. For., 18, 87-94.
Pormajidian M.R., 1992. Researches in relation to results of afforestation with Picea abies in Kelardasht region. M.Sc. thesis: Tehran University (Iran).
Ratkowsky D.A., 1990. Handbook of non-linear regression models. New York, USA: Marcel Dekker, Inc.
Ratkowsky D.A. & Reedy T.J., 1986. Choosing near-linear parameters in the four-parameter logistic model for radioligand and related assays. Biometrics, 42, 575-582.
Richards F.J., 1959. A flexible growth function for empirical use. J. Exp. Bot., 10, 290-300.
Sagheb-Talebi Kh., Yazdian F. & Sajedi T., 2004. Forests of Iran. Tehran: Research Institute of Forests and Rangelands (RIFR).
Ritchie M.W. & Hann D.W., 1986. Development of a tree height growth model for Douglas-fir. For. Ecol. Manage., 15, 135-145.
Sánchez C.A.L. et al., 2003. A height-diameter model for Pinus radiata D.Don in Galicia (Northwest Spain). Ann. For. Sci., 60, 237-245.
SAS Institute Inc., 2002. SAS/ETS1 9.1 User’s Guide. Cary, NC, USA: SAS Institute Inc.
Schabenberger O. & Pierce F.J., 2002. Contemporary statistical models for the plant and soil sciences. Boca Raton, FL, USA: CRC Press.
Schnute J., 1981. A versatile growth model with statistically stable parameters. Can. J. Fish. Aquat. Sci., 38, 1128-1140.
Sharma R.P., 2009. Modelling height-diameter relationship for Chir pine trees. Banko Janakari, 19, 3-9.
Sharma M. & Zhang S.Y., 2004. Height-diameter models using stand characteristics for Pinus banksiana and Picea mariana. Scand. J. For. Res., 19, 442-451.
Sharma M. & Portan J., 2007. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modelling approach. For. Ecol. Manage., 249, 187-198.
Shifley S.R. & Braud G.J., 1984. Chapman-Richards growth function constrained for maximum tree size. For. Sci., 30, 1066-1070.
Siahipour Z., Rostami T., Taleb S. & Taheri K., 2002. Investigation of sustainable Picea abies in afforestations of Guilan province. For. Poplar Res. Iran, 312, 1-53.
Spurr S.H., 1952. Forest inventory. New York, USA: The Ronald Press Company.
Stage A.R., 1963. A mathematical approach to polymorphic site index curves for grand fir. For. Sci., 9, 167-180.
Staudhammer C. & Lemay V., 2000. Height prediction equations using diameter and stand density measures. For. Chron., 76, 303-309.
Tomé M., 1989. Modelaçao do crescimento da árvore individual em povoamentos de Eucalyptus globulus Labill. (1ª rotaçao) na regiao centro de Portugal. PhD. thesis: Instituto Superior de Agronomía, Lisboa (Portugal).
Van Deusen P.C. & Biging G.S., 1985. STAG. A STAnd Generator for mixed species stands. Version 2.0. Research note No. 11. Berkeley, CA, USA: Northern California Forest Yield Cooperative, Department of Forestry and Resource Management, University of California.
Vanclay J.K., 1994. Modeling forest growth and yield: applications to mixed tropical forests. Wallingford, UK: CABI.
Vanclay J.K. & Skovsgaard J.P., 1997. Evaluating forest growth models. Ecol. Modell., 98, 1-12.
Wykoff W.R., Crookston N.L. & Stage A.R., 1982. User's guide to the Stand Prognosis Model. General technical report INT-122. Ogden, UT, USA: USDA, Forest Service, Intermountain Forest and Range Experiment Station.
Yang R.C., Kozak A. & Smith J.H.G., 1978. The potential of Weibull-type functions as a flexible growth curves. Can. J. For. Res., 8, 424-431.
Zeide B., 1989. Accuracy of equations describing diameter growth. Can. J. For. Res., 19, 1283-1286.
Zeide B., 1993. Analysis of growth equation. For. Sci., 39, 594-616.
Zhang L., 1997. Cross-validation of non-linear growth functions for modeling tree height-diameter relationships. Ann. Bot., 79, 251-257.
Zhang L., Moore J.A. & Newberry J.D., 1996. Evaluation of the prediction performance for eight nonlinear height-diameter equations. In: Proceedings of the 1995 Society of American Foresters Convention. SAF-96-0l. Bethesda, MD, USA: SAF Publications, 447-448.
Para citar este artículo
Acerca de: Kourosh Ahmadi
Tarbiat Modares University Faculty of Natural Resources and Marine Sciences. Department of Forestry. Imam Reza St. Nour. Mazandaran Province (Iran).
Acerca de: Seyed Jalil Alavi
Tarbiat Modares University Faculty of Natural Resources and Marine Sciences. Department of Forestry. Imam Reza St. Nour. Mazandaran Province (Iran). E-mail: j.alavi@modares.ac.ir
Acerca de: Masoud Tabari Kouchaksaraei
Tarbiat Modares University Faculty of Natural Resources and Marine Sciences. Department of Forestry. Imam Reza St. Nour. Mazandaran Province (Iran).
Acerca de: Wim Aertsen
Katholieke Universiteit Leuven. Division Forest, Nature and Landscape. Celestijnenlaan 200E-2411. B-3001 Leuven (Belgium).