Mathieu Massinon & Frédéric Lebeau

Review of physicochemical processes involved in agrochemical spray retention

Attached document(s)

Annexes

• pdf (351k)

Résumé

Synthèse bibliographique des processus physicochimiques impliqués dans la rétention de produits phytosanitaires. Cette synthèse bibliographique propose une vue d'ensemble des processus et des paramètres impliqués dans l'application des produits phytosanitaires en grandes cultures. L'efficacité du traitement est envisagée par des approches macroscopique et microscopique au niveau de la rétention. Au point de vue macroscopique, les études liées à la granulométrie du jet, au volume par hectare, à la mouillabilité des feuilles, à l'architecture et à la densité de la canopée ainsi qu’aux additifs sont abordées. Ces études comparatives mettent en évidence la grande variabilité de la rétention en fonction de ces paramètres. Cependant, elles ne parviennent pas à clarifier les relations physiques sous-jacentes qui sont nécessaires à une généralisation de leurs résultats. Ces relations sont de préférence étudiées en utilisant une approche microscopique. Dans ces études, le comportement à l’impact des gouttes en relation avec la surface de la cible et les propriétés du fluide est établi. Le régime de mouillage, décrit soit par le modèle de Wenzel ou de Cassie-Baxter, dépend de la rugosité microscopique de la surface foliaire et de sa nature chimique, de la tension de surface dynamique du fluide et de l'énergie d'impact des gouttes. L’adhésion, le rebond et la fragmentation sont successivement observés au fur et à mesure que l'énergie d'impact des gouttes augmente. Les transitions entre ces résultats sont influencées par la rhéologie et la tension superficielle dynamique du fluide. L’effet de l’angle de la surface est encore mal exploré, mais semble avoir une influence limitée. Les recherches fondamentales récentes sur la superhydrophobicité et le mouillage devraient assister les praticiens dans leur quête d'une application des produits phytosanitaires de plus en plus rationnelle. Elles pourraient également conduire au développement de nouvelles méthodes d'essais systématiques de la rétention.

Abstract

This review provides a broad view of the processes and parameters involved in applying agrochemicals to the leaves of field crops. Treatment efficiency is assessed using macroscopic and microscopic approaches to investigate spray retention. With the macroscopic approach, aspects related to spray coarseness, carrier volume, leaf wettability, plant architecture, crop density and additives are addressed. Comparative studies have highlighted the wide variability in spray retention as a function of these parameters. They have failed, however, to describe the underlying physical relationships clearly enough to generalize the results. These relationships are better investigated using a microscopic approach, where drop impact behavior is established in relation to target surface and fluid properties. The wetting regime (either Wenzel or Cassie-Baxter) depends on the leaf surface microscopic roughness ratio (r) and chemical nature, fluid dynamic surface tension and drop impact energy. Adhesion, rebound and disintegration have been observed successively with increasing drop impact energy. Transitions between impact outcomes are influenced by fluid rheology and the dynamic surface tension of the fluid. The effect of surface orientation remains poorly explored, but it seems to have a limited influence on retention. Recent fundamental studies on superhydrophobicity and wetting should help practitioners in their search for an ever more rational application of agrochemicals. They could also drive the development of new systematic retention testing methods.

Table of content

1. Introduction

1Crop protection is still achieved mainly by using pesticides. Most products are sprayed over the intended target surface as uniformly as possible, using boom sprayers equipped with equally spaced hydraulic nozzles releasing drops with a wide size distribution into the air. Current practice is to estimate the mean infestation level over the whole field and decide whether or not to treat. Farmers can adjust the carrier volume applied by modifying nozzle kind or size, liquid pressure and sprayer travel speed. The choice of the formulation is also critical in efforts to improve spraying performance since active ingredients in their raw state are usually not suitable for pest control. Pesticide formulation consists of a set of industrial processes designed to improve the properties of a chemical for handling, storage, application and may substantially influence effectiveness and safety. Farmers can also use tank mix adjuvants to improve their treatment. Adjuvants include any materials used as compatibility agents, drift retardants, suspension aids, spray buffer or surfactants. The spray mixture is therefore highly complex and the interaction between drop and leaves as well as spray characteristics can be greatly modified. The target itself introduces additional variation sources, such as species, leaf orientation, canopy density, age, position on the leaf and weathering. Much work has been done on maximizing spraying efficiency by optimizing each step of the process, i.e. deposition (spray formation and transport to the target), retention (amount of product captured by the crop), uptake (amount of active ingredient absorbed into plant foliage) and translocation (amount of absorbed material translocated) (Wirth et al., 1991; Zabkiewicz, 2007). The aim was to adjust and apply the optimal dose in order to ensure the required level of crop protection while minimizing wastage and pollution.

2This paper deals with spray retention, which can be studied using two approaches. The first is the macroscopic approach, based on quantifying retention using an integrative measurement method for the whole plant or leaf. Input variables include nozzle type, formulation, adjuvant type and concentration, and target. The second is the microscopic approach, which focuses on the drop impact dynamic and investigates the interactions between the liquid and the surface (wetting) at drop scale. Although macroscopic studies are designed to select the most effective application method under realistic field conditions, microscopic studies can highlight the physics behind performance differences and elicit more detailed information of value for systematic developments. The paper reviews the whole retention process by plant surfaces, from both the macroscopic and microscopic points of view. The review should help practitioners achieve optimal spray retention and guide the development of new testing methods for optimizing biological efficacy.

2. Phenomenological or macroscopic view

3Selecting an optimal application technology has been investigated in many retention studies. Usually, a tracer is added to the sprayed formulations and the retained content is measured after washing one leaf or the whole plant. Gravimetric methods and active ingredient dosage are also used (Wirth et al., 1991). Retention is expressed by the volume of spray solution retained per unit of plant dry weight or surface area, the results being statistically interpreted to highlight any significant differences (Furmidge, 1962; Butler Ellis et al., 2004; Byer et al., 2006).

2.1. Spray nozzle classification and carrier volume

4In general, finer sprays result in better retention of foliar-applied herbicides for a constant carrier volume, whatever the drop size range investigated (Skuterud et al., 1988; Knoche, 1994). This was shown, for example, on corn (Zea mays L.) (Feng et al., 2003) and green foxtail (Setaria viridis [L.] P.Beauv.) (Peng et al., 2005). The spray coarseness induced different responses, however, depending on the species. Retention is reduced by increasing spray coarseness when applied to the difficult-to-wet giant foxtail (Setaria faberi Herrm), but no influence was evident in the case of smooth pigweed (Amaranthus hybridus L.) (Wolf et al., 2000). The flat-fan nozzles resulted in higher retention than air-induction nozzles, and this efficacy gap grew with the dynamic surface tension (Butler Ellis et al., 2004). Reducing the carrier volume to below 100 l·ha^-1 reduces retention performance more often than a carrier volume above 400 l·ha^-1. On difficult-to-wet species, however, reducing carrier volume increases retention more often than on easy-to-wet plants (Knoche, 1994). The possible reasons for these differences are often related to plant properties.

2.2. Plant properties

5Plant architecture and crop canopy. Regardless of spray drift, plant architecture and canopy density modify drop interception by leaves. There is a higher probability that a drop will hit a leaf in high plant density conditions with high density sprays. In a very dense canopy of wheat where the leaf area index (LAI) was high, retention was independent of liquids and nozzles tested, whereas for lower densities there appeared to be clear differences between formulation retention, whatever kind of nozzle tested (Butler Ellis et al., 2004). Leaf orientation varies with growth stage and species. A thin, vertical leaf, such as blackgrass (Alopecurus myosuroides Huds.) at an early growth stage, is very difficult to treat because of the low LAI and the limited projected area available for intercepting the drops. With such challenging targets, increasing the proportion of drops with a diameter below 150 μm enhanced the performance more consistently than for drops above 150 μm (Knoche, 1994). With small drops there is a more homogeneous distribution of the active substance on the leaves because of the higher spray density. Fine drops are better retained by plants at impact, but they are also more sensitive to small air turbulences. They can penetrate deeper within the canopy and even reach leaf undersides. They are more sensitive to drift and evaporation, however, than larger drops. This indicates the importance of drop size and spray density in relation to crop canopy density. In addition to plant architecture, leaf wettability is a crucial parameter in explaining differences recorded in field retention trials.

6Leaf wettability and equilibrium contact angle. Leaves are often ranked according to their wettability. Leaf surfaces vary widely from easy-to-wet to very difficult-to-wet (Zabkiewicz, 2007). Wettability is a thermodynamic property of the solid-liquid-gas interface defined by the equilibrium contact angle. On ideal dry smooth surfaces, the equilibrium contact angle is given by Young’s equation:

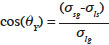
7where σ_lg, σ_ls σ_sg are the interfacial tensions (N·m^-1) at the boundaries of the liquid-solid-gas system. The equilibrium contact angle is measured at the point where the liquid, solid and gas interfaces meet, known as the “contact line”. The mechanism for spontaneous drop spreading on a solid surface towards equilibrium depends on a disparity in the interfacial tensions at the contact line: if the solid/gas tension is greater than the sum of the two others, the drop spreads until the balance is restored (Nikolov et al., 2002). The equilibrium contact angle is independent of drop size (Quéré, 2005). It is sometimes referred to as “apparent contact angle” because it is the macroscopic behavior of liquid/surface interactions. The more the drop spreads on the surface, the more the surface is wet by the liquid and the smaller the contact angle. The lower the surface tension, the faster the drop spreads.

8Leaf classification is important in order to predict effective retention and liquid behavior. This is very helpful for identifying appropriate application techniques and agrochemical requirements for species. Since agrochemical formulations are complex and often designed for maximum spread, it is sometimes difficult or impossible to measure any contact angles. The contact angle of pure water, however, is not always appropriate for differentiating between species (Gaskin et al., 2005). On very difficult-to-wet species, the water contact angle is too high and no significant differences can be highlighted. It was therefore proposed to use a 20% v/v acetone in water solution to reduce surface tension. The wettability of leaf surfaces depends on species, variety, growth stage, leaf position, growth conditions and environmental factors, hence the retention variations observed in field trials. Overall, leaf wettability can change with age and maturity, but no trend has been identified, although wheat leaves become less hydrophobic with age (Butler Ellis et al., 2004). Wettability modifications could originate from fouling and sandblasting from wind-borne particles of leaves, indoor-grown leaves being more hydrophobic. When performing laboratory tests using indoor-grown plants, therefore, the findings cannot be directly extrapolated to field, although the leaves are able to regenerate their waxes after a few days. Leaf surface properties (e.g., wettability, as affected by dew, rain, sandblasting or dust) before the day of treatment should be integrated into the results analysis or used to help decide on the optimum time of treatment.

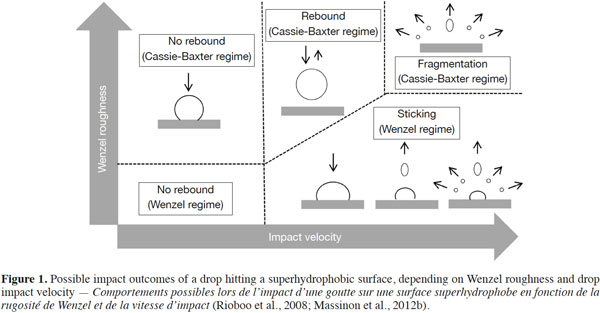
2.3. Additives

9The difficult-to-wet leaf issue is often addressed using additives. Surfactants promote drop spreading on surfaces by reducing surface tension and the advancing and receding contact angles (sections 3.2. and 3.3.). Their effects depend on concentration, leaf surface properties and application volumes (Gaskin et al., 1997). Overall, the use of surfactant increases retention by plants, which increases pesticide efficiency. The beneficial effect grows with surfactant concentration (Wirth et al., 1991) until a concentration threshold is reached above which there will be no further retention improvement (Furmidge, 1962). Easy-to-wet species exhibit no variation in retention because they are made wet by water (high surface tension). The differences in retention between surfactants are closely correlated to the dynamic surface tension (DST) of the spray mixture; DST refers to surface tension variation over time. If the surfactant adsorption time is greater than the drop impact, the surfactant effect can be greatly reduced or even negated. This will be discussed further in section 3.4.

10Additives also affect jet break-up. Smaller drops are produced by reducing the surface tension and viscosity of the sprayed formulation. Thus, the volume median diameter (VMD) is modified, as are the leaf impact conditions. Although smaller drops are favorable for retention, they are more prone to drift. Liquid DST has to be considered in spray formation because surface tension governs break-up type. Surfactants can produce drops that include air, which reduces drop liquid density and affects drop transport (Butler Ellis et al., 1997) and behavior at impact. Much information about the physics of drop formation is available (Sirignano et al., 2000). Finally, liquid properties affect drops formation, trajectory and impact on the target. An optimum approach between formulation and application technique has to be found in order to maximize retention while minimizing drift.

2.4. Discussion on phenomenological studies

11Macroscopic studies are conducted to gain a better understanding of a complex process, performing tests in specific and variable conditions. They successfully identify some general trends and the main variables involved in spray retention by leaves. Since many variables change between trials, it is not easy to generalize the findings. These studies are very educational and have provided the impetus to improve spray efficiency, but a thorough understanding of each mechanism involved in this complex process is needed. Therefore, the physics at drop scale has to be understood because retention is determined mainly by the fate of all drops sprayed.

12Drop generators have often been proposed for systematic studies on the effect of physiochemical parameters on retention (Lake, 1977; Reichard et al., 1998; Webb et al., 1999; Forster et al., 2005). Using such apparatuses, however, has reinforced the perception of spray retention on leaves as a two-state process. A drop may either adhere to or bounce off the target because these apparatuses shift the focus mainly to the effect of drop size. Since drops are released into the air without initial velocity, impact always occurs at or below terminal velocity, depending on release height. Adhesion is then assimilated to retention. Shattering has seldom been observed because of insufficient drop energy at impact. The development of affordable high-speed cameras and the use of dimensional analysis to simplify the relationship between variables (Lake et al., 1983) encouraged many studies to be conducted on the dynamic of drop impact. Some of the current techniques for studying retention use real agricultural nozzles and generate all impact outcomes likely in practical conditions (Massinon et al., 2012b).

13The points addressed in section 2 will therefore be discussed from the microscopic perspective in section 3. Leaf surfaces are described in section 3.1., the various wetting models developed are presented in section 3.2., the resulting impact regimes in section 3.3 and the effect of liquid properties on drop impact in section 3.4.

3. Microscopic perspective

3.1. Leaf surfaces

14The wetting and subsequent drop impact behavior is determined mainly by the structure of the outermost layers of plant surfaces. A study of the lotus effect and self-cleaning surfaces has emphasized the importance of the micro-structure and even of the nano-structure of the surface on wetting (Koch et al., 2009). The outermost layer of the epidermis contains a cuticle that creates the structure of folds and subcuticular inserts which are covered by epicuticular waxes. This coating helps prevent leaf colonization by bacterial pathogens and controls plant humidity. The epicuticular waxes are crystalline; their size ranges from 0.2 to 100 µm and there is a wide diversity of morphological types, including films, crusts, tubules, platelets, rodlets and transversely ridged rodlets (Barthlott et al., 1998). These characteristics give leaf surfaces extreme water repellency making such targets very difficult-to-treat, especially at early growth stages. Mechanisms involved in the wetting of leaf surfaces by agrochemicals are reviewed in Taylor (2011).

3.2. Spontaneous wetting of rough surfaces and superhydrophobicity

15The wetting of rough surfaces is often described in two models based on Young’s equation. In the first situation, an increase in the surface area due to the micro-texture enhances the hydrophobicity of the material compared with Young’s ideal model. The liquid fills the rough grooves completely. The drop replaces the air trapped in the surface roughness and fits into the microstructure of the material. This situation is referred to as non-composite, homogeneous, sticking or pinning wetting regime and is described by the Wenzel regime (Wenzel, 1936):

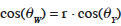
16where r is the ratio of the true wetted area to the projected planar surface area (always greater than unity), θ_W is the apparent angle and θ_Y is the Young angle. The second situation describes the wetting of rougher (porous) surfaces where air pockets are trapped in the surface texture beneath the liquid. The drop contacts only the top of the surface asperities. This situation is described by the Cassie-Baxter regime (Cassie et al., 1944):

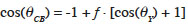
17where f is the fraction of the solid/liquid interface (the liquid contacts the solid only through the top of the asperities on a fraction f) and θ_CB is the apparent contact angle.

18An irreversible transition from Cassie to Wenzel wetting state is possible (Nosonovsky et al., 2007) and depends on how the drop comes into contact with the surface (gently deposited or impacted) (He et al., 2003), the ratio of drop size to roughness scale (Bartolo et al., 2006; Reyssat et al., 2006; Marmur, 2008), topography parameters and pattern density (Callies et al., 2005). If the pattern density is very low, the drop reaches the Wenzel state because there is not enough contacting surface to sustain the liquid, which sinks into the surface texture. This can occur by increasing the drop impact velocity for a surface that exhibits a Cassie-Baxter state at lower speeds. This is referred to as pinning and is caused by a high contact angle hysteresis. In forced wetting, apparent contact angle may not be single-valued and depends on whether the moving contact line is advancing or receding (Blake, 2006) on a rough surface containing hydrophilic blemishes (Chang et al., 2009). Difference between advancing and receding contact angles is called “contact angle hysteresis”. Apart from some exceptions, observed for instance in the leaves of some plants such as garlic (Chang et al., 2009), superhydrophobic surfaces are defined by the high contact angles (above 150º) and their low hysteresis. Using these models, section 3.3. describes the possible drop impact outcomes on solid surfaces.

3.3. Impact outcomes of single drop

19Drop impact on a dry solid surface can be divided into four successive phases (kinematic, spreading, relaxation and equilibrium phase), based on the dimensionless spread factor d* = d∙D₀^-1, where D₀ is the drop diameter before impact and d is the spread diameter after a time t (Rioboo et al., 2002). Dimensionless height h* = h∙D₀^-1 is also useful for characterizing impact outcome (Crooks et al., 2001). Dimensionless parameters enable a comparison to be made between drops of various sizes.

20The kinematic phase is the initial phase of impact. The bottom of the drop is stopped at impact, but the upper part of the drop is still moving. The drop takes a truncated shape (initially spherical), the wetted spot increases and the dimensionless height decreases over time. The bottom of the drop begins to spread out on the surface as a thin film. The spreading is triggered by a shock wave created at impact because of liquid compression (Rein, 1993). Inertial forces dominate during this first phase and the spread factor increases with the square root of dimensionless time (t* = t∙V∙D₀^-1) where V is the drop velocity at impact. Before impact, a drop contains a certain amount of kinetic energy:

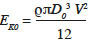
21where ρ is the fluid density (kg·m^-3). Some of the kinetic energy is converted into surface energy as a result of drop deformation. The initial surface energy is computed as:

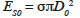
22where σ is the surface tension of the liquid (N·m^-1). This phase ends at approximately t* = 0.1. Wettability has no influence, neither do the viscous forces.

23In the second phase, the liquid lamella (spreading disk) is spread on the surface. The lamella is bordered by a rim caused by surface tension. The contact line moves radially in the direction of the gas (Šikalo et al., 2005b). The contact angle established during this phase is called the “advancing contact angle” θ_A. Spreading increases and the contact line acceleration decreases towards the end of the spreading phase. This is because of the dissipation of the drop’s kinetic and surface energy by viscous processes into additional surface energy (Rein, 1993). The maximum spread diameter is smaller and reached earlier when viscosity is increased. This trend is identical for impact velocity. For determining the maximum spread diameter and the time taken to reach it, most approaches apply the laws of energy conservation to the spreading lamella (Rein, 1993; Mundo et al., 1995; Moreira et al., 2011), assuming the event is adiabatic:

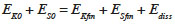
24where E_k is the drop’s kinetic energy (J), E_s is its surface energy (J), E_diss is the energy dissipated by viscous effects (J) and subscript 0 denotes the state before impact and fin the final state. The final state is taken at the maximum spread diameter.

25When dissipation overcomes the inertial energy, spreading stops and the drop reaches its maximal spreading diameter. The contact angle then decreases, becoming “the receding contact angle”, and the contact line begins to recoil on an already wetted surface (relaxation phase). The recoil is initiated by the dominating surface forces, with the liquid trying to restore the drop shape that minimizes the free surface energy. The contact angle hysteresis greatly influences impact outcome (Quéré, 2005). If hysteresis is high and viscous forces dissipate the kinetic energy, the drop adheres to the surface. Drop oscillations dissipate the remaining energy at impact. If kinetic energy remains after viscous dissipation, the drop may splash or shatter. Splashing is the result of the drop disintegrating into two or more secondary drops after landing on the surface. It occurs because of the instability of the spreading lamella and depends on surface roughness. Finally, the equilibrium or wetting phase ends the impact outcome. If hysteresis is low and the advancing contact angle is high, a total rebound can occur, depending on impact velocity.

26A map of impact behavior according to surface roughness and impact energy was built from experimental investigations on artificial superhydrophobic porous surfaces (Figure 1) (Rioboo et al., 2008). For low Wenzel roughness, a drop of low kinetic energy is deposited in a Wenzel state. By gradually increasing its kinetic energy, the drop is fragmented. Depending on impact energy, a single satellite drop (referred to as “partial rebound”) or several satellite drops (referred to as “pinning fragmentation”) can leave the surface, whereas the rest of the drop adheres to the impact point. For intermediate Wenzel roughness, low velocity drops adhere in a Cassie-Baxter regime. With increasing speed, the drop bounces completely. If impact pressure is great enough or liquid surface tension low enough, the liquid can penetrate the surface roughness, modifying the wettability regime from Cassie-Baxter to Wenzel. Thus, sticking, partial rebound or pinning fragmentation can be observed. Finally, for high Wenzel roughness, a drop can adhere in a Cassie-Baxter regime, rebound or splash completely, depending on impact velocity. If it splashes, all the liquid is shattered into numerous satellite drops and leaves the surface.

27Drop impact involves many forces that can be grouped in dimensionless numbers (Table 1), characterizing the relative magnitude of the forces acting on the drop. Dimensional analysis is usually used to simplify the relationships between the variables involved (Lake et al., 1983) and to build threshold criteria for establishing boundaries between impact outcomes and for forecasting impact behavior on the basis of drop properties before impact and surface properties. More information about threshold criteria can be found in Mundo et al. (1995), Range et al. (1998), Cossali et al. (2005), Yarin (2006) and Moreira et al. (2010).

28The effects of drop impact on an angled leaf surface still need to be clarified, although much work has been done (Wirth et al., 1991; Forster et al., 2005; Bird et al., 2009; Massinon et al., 2012a). The main effects related to increase in leaf angle are:

29– a reduction in the projected area available for spray drops, and therefore a reduction in the number of impacts per unit area of leaf;

30– a reduction in the normal velocity component at impact.

31Rebound occurs if the drop does not have enough kinetic energy to undergo a transition from a Cassie-Baxter to Wenzel wetting regime by expelling the air trapped in the surface roughness. Overall, a reduction in the normal velocity component by an increase in leaf angle leads to partial and total rebound (Yarin, 2006). The use of the normal velocity component has been proposed for computing the dimensionless number: for low impact angles (< 35°), the Weber number at which the rebound occurs is constant if the normal velocity component is used in computing the Weber number. The drop can also slip, depending on impact angle, liquid and surface properties and impact energy (Šikalo et al., 2005a).

3.4. Effect of liquid properties on drop impact

32Surface tension. In the first two phases of drop impact, the equilibrium surface tension has a negligible effect on the spread factor because these phases are dominated by inertial and viscous forces (Crooks et al., 2001). If the drop contains molecules of surfactant, the recoil phase is subdued. Overall, two outcomes are possible: either the drop splashes because of an excess of kinetic energy (high Weber number), or it remains spread if the viscous dissipations are large enough. However, the rebound is not always eliminated by surfactants, for reasons given below.

33Immediately before impact, a drop is spherical and surface tension has reached the equilibrium value. During drop deformation, the surface area of the liquid/gas interface increases quickly (< 2 ms). Surfactant molecules of the bulk solution migrate to the surface to fill the gaps by adsorption. If the surfactant concentration is below the critical micelle concentration (CMC), three mechanisms for surfactant distribution along the liquid/gas interface have been proposed (Zhang et al., 1997). First, there is a dilution of the surfactant due to the creation of a new surface area. Second, there is a convection of the surfactants towards the contact line that accumulate at the moving front during spreading, increasing the maximum spread diameter and inhibiting the recoil phase. This effect, however, was not reported by Crooks et al. (2001). Third, there is a repopulation of the interface by the surfactants. It is the drop hydrodynamics, therefore, that control the surfactant concentration in bulk solution. If the surfactant concentration is above the CMC, a demicellisation occurs, keeping the surfactant concentration constant in the bulk solution and supplying surfactant molecules for the new surface created during impact. If the demicellisation time rate is higher than the transport and adsorption of free molecules to the surface, the accumulation of surfactant molecules by convection at the moving edge is overcome and surface tension is dramatically reduced. Since the timescales of the initial phases of drop impact are very short, the adsorption rate and concentration of surfactants in the drop play an important role in the fate of an impacting drop by modifying the dynamic surface tension. In order to guarantee continued spreading, the surfactant adsorption rate at the contact line must exceed the diluting effect of area expansion (Venzmer, 2011). Overall, the reduction of surface tension by surfactants increases spreading and reduces recoil. Depending on the kinetic of surfactant adsorption and surface energy, a drop can still rebound off the surface (Mourougou-Candoni et al., 1997). In addition, lower surface tension favors splashing.

34Although the first phase of drop impact is governed mainly by inertial energy, especially when the DST is high, a description of the drop spreading mechanism could be useful in improving the overall understanding of pesticide efficiency. Three mechanisms can promote spreading:

35– reducing the liquid/gas tension by the adsorption of surfactants at this interface,

36– reducing the solid/liquid tension by the adsorption of surfactant molecules on the substrate,

37– by increasing the solid/gas tension when surfactants are adsorbed in front of the moving contact line (Starov et al., 2010; Ivanova et al., 2011).

38The adsorption of surfactant molecules on a bare hydrophobic surface in front of the contact line is a spontaneous process. Since that process leads to an increase in the local solid/gas interfacial tension, the adsorption goes via a potential barrier, which is the change in local free energy caused by the jump of a single surfactant molecule from the liquid/gas interface on the surface. Organosilicone (trisiloxane) surfactants promote rapid spreading of the drop even on (super)hydrophobic substrates. They are frequently used in the composition of agrochemicals. The reasons for superspreading, however, are not fully understood and various explanations have been proposed. Nikolov et al. (2002) suggested that superspreading could be driven by Marangoni flows, whereby the expansion of the contact line stretches the drop surface area, reducing local surfactant concentration. The surface tension at the edge of the spreading drop is then higher than that in the center, creating a surface tension gradient. The Marangoni stresses drive the liquid from the lower to the higher surfactant concentration, leading to drop spreading. This contradicts the classic wetting described in section 2.2., where spreading requires low surface tension in the drop. Other possible reasons for controverted superspreading have been discussed by Venzmer (2011).

39Viscosity. Spraying viscous products is not common in pesticide application because of pumping problems. Viscosity could, however, have a beneficial effect on spray retention. An increase in shear viscosity reduces a drop’s maximum spreading diameter (Clanet et al., 2004) and reduces the tendency to bounce on dry surfaces (Caviezel et al., 2008). Viscosity exhausts the energy stored in the drop by deformation, but this effect is offset by high surface tension. The splashing of a viscous liquid drop differs in that it develops slowly and fragmentation is reduced.

40More recently, it has been shown that the use of polymer additives enhances spray deposition and retention on a plant surface. A small amount of flexible polymer added to the aqueous phase can inhibit drop rebound by increasing elongational viscosity (Bergeron, 2003). The surface tension and shear viscosity of the solution are not affected by these polymers. Stretching such solutions unfolds and deforms the polymer molecules, which drains drop energy. Splashing is reduced because the elongational viscosity stabilizes the capillary instabilities responsible for fragmentation. Polymer solutions also have a great influence on atomization by stabilizing the perturbations that drive jet break-up (Mun et al., 1999). Adding polymers to spray solution increases the VMD, reduces the proportion of fine drops and improves treatment efficacy (Jones et al., 2007). The use of such additives therefore also reduces the drift potential of the application.

3.5. Discussion on microscopic studies

41The numerous studies on the dynamic of single drop impact reveal the complexity of the process and the influence of many factors on the fate of a single drop. These studies are needed to understand the mechanisms that are relevant for retention, but involve sprays with various energy drops. In this context, some aspects should also be addressed in retention studies.

42For instance, drop impact behavior is affected by the accumulation of a liquid film on leaf surface (Rein, 1993; Roisman et al., 2006; Yarin, 2006; Kalantari et al., 2007; Moreira et al., 2010), although this is now rarely observed in field application because of the ever lower volumes per hectare applied (below 150 l·ha^-1), the small drop sizes, the spray boom displacement, the granulometric drop sorting during the fall, the leaf wettability and the canopy architecture. Furthermore, secondary drops produced by drop disintegration can be directly lost on the soil or be captured by the same or another leaf in a dense canopy. The amount of product remaining on the leaf surface after a drop impact in Wenzel wetting state has still to be assessed to gain a better correlation between impact behavior and retention. Finally, hydrophobic defects caused by fouling, sandblasting and/or epicuticular compounds, as well as leaf elasticity dissipating the drop kinetic energy by leaf bending for large drops and reducing the likelihood of bounce (Forster et al., 2005), increase the variability in trials.

43Microscopic studies provide no information on the biological efficiency of pesticides, but provide physical reasons for differences in retention. They could, however, help in the design of more discriminating field experiments and efficient actuators (nozzles, spot spraying) to meet the objectives of precision spraying.

4. Conclusion

44Retention is a key factor in spraying efficiency. In order to reduce environmental contamination, it has to be perfectly understood and mastered. The physicochemical properties of spray mixtures and their application techniques need to be optimized for a given leaf application, integrating an optimum time of spraying.

45Losses caused by drop rebound and disintegration have to be limited or avoided although their negative effects can be reduced or absent in very dense canopies. Depending on species (growth stage and surface wettability), an optimal drop impact energy should be found to limit undesirable effects. This can be achieved by adjusting drop size and velocity distributions by choosing the best combination between nozzle, pressure and spray mixture properties (such as surface tension and viscosity) that alter both drop impact and spray formation. The use of surfactants with very low DST for reducing drop rebound and promoting spreading is well known. The use of non-Newtonian additives to exhaust drop impact energy is, however, less common although the promising perspectives of Bergeron (2003). Actuators such as rotary atomizers or splash plate nozzles generating sharper drop size distribution centered on the required VMD should also be considered for optimizing spray retention.

46As already done for spray characterization, the development of methods that could measure and/or predict the efficiency of any given application technique in terms of spray impact would be very useful for users and researchers. Some progress has been made using high-speed imaging, a synthetic superhydrophobic surface and agricultural sprays, leading to all the impact outcomes encountered in field (Massinon et al., 2012b). The development of recipes and tank mix adjuvants can be optimized using such methods for maximizing spray retention by leaves. These methods should ultimately be able to provide the spray volume proportions for each impact type and be related to retention using macroscopic approaches. Further research is also needed on clarifying some aspects, such as leaf orientation, surface elasticity and polymer additives.

47List of abbreviations, symbols and subscripts

48Abbreviations

49Ca: capillary number

50CMC: critical micelle concentration, mol.l-1

51d: drop spreading diameter, m

52d^*: dimensionless spread factor for a time t

53D₀: drop diameter before impact, m

54DST: dynamic surface tension, N·m^-1

55E_K: drop kinetic energy, J

56E_S: drop surface energy, J

57h: drop height on the surface during impact, m

58h^*: dimensionless drop height for a time t

59LAI: leaf area index, leaf surface area·soil area^-1

60Oh: Ohnesorge number

61r: roughness ratio, true wetted area·projected planar surface area^-1

62Re: Reynolds number

63t: time measured from the instant of impact, s

64t^*: dimensionless spreading time

65V: drop velocity, m·s^-1

66VMD: volume median diameter, µm

67We: Weber number

68Symbols

69σ: surface tension, N·m^-1

70θ: contact angle, °

71μ: liquid viscosity, Pa.s

72ρ: liquid density, kg·m^-3

73Subscripts

74c: critical

75lg: liquid-gas

76ls: liquid-solid

77sg: solid-gas

780: state before impact

79Y: Young

80W: Wenzel

81CB: Cassie-Baxter

82fin: final state

83A: advancing

84R: receding

Bibliographie

To cite this article

About: Mathieu Massinon

About: Frédéric Lebeau