Mohamar Moussa Ouédraogo, Charles Debouche & Aurore Degré

Influence de l'état d'ameublissement et de la rugosité du sol des parcelles agricoles sur l'exactitude de l'altitude des points de contrôle positionnés au GPS

Document(s) associé(s)

Annexes

• pdf (332k)

Résumé

Notre objectif est d'estimer à travers des intervalles de variation, l'influence de l'état d'ameublissement et de la rugosité des parcelles agricoles, conséquences des outils de travail du sol, sur l'exactitude de l'altitude des points de contrôle positionnés au GPS (Global Positioning System) en mode RTK (Real Time Kinematic). Pour cela, des levés de l'altitude de 16 points (avec une distance de 100 mm entre les points) ont été réalisés d'abord à la Station Totale (ST), puis au GPS RTK sur 6 transects dans 2 parcelles (3 transects par parcelle). Les techniques culturales pratiquées sur les deux parcelles sont différentes. La parcelle 1 est labourée, la parcelle 2 a subi un travail du sol pour le semis du froment. L'analyse de la variance est ensuite appliquée aux écarts d'altitude obtenus entre ST et GPS RTK pour estimer l'intervalle de variation dû à l'ameublissement du sol, tandis que la méthode de la décomposition en série chronologique est appliquée aux données GPS RTK pour estimer l'intervalle de variation dû à l'influence de la rugosité du sol. Ces intervalles de variation des altitudes dans les parcelles 1 et 2 sont respectivement [51 mm ; 57 mm], [-4 mm ; 4 mm] et [97 mm ; 113 mm], [-35 mm ; 23 mm]. Ces résultats montrent que l'exactitude des points de contrôle est influencée d'une part par l'état d'ameublissement du sol des parcelles, et d'autre part par leur rugosité. Nous pouvons en conclure que l'état d'ameublissement et la rugosité ont une influence non négligeable sur l'exactitude des points de contrôle localisés sur les parcelles agricoles. Cette influence devra être considérée dans l'évaluation de l'exactitude des modèles numériques de terrain des bassins versants agricoles.

Abstract

Agricultural soil tilth and roughness impact on the exactness of ground control points elevation surveyed by GPS. Our goal in this study is to estimate through ranges of variation, the impact of agricultural parcels soil's tilth and roughness, due to cultivation techniques, on the exactness of ground control points elevation surveyed by RTK (Real Time Kinematic) GPS (Global Positioning System). So, 16 point's elevations which were located each 100 mm on a transect have been surveyed first by using a Total Station (TS), and then a RTK GPS in 2 parcels (3 transects per parcel). Cultivation techniques on those parcels were different. The parcel 1 was tilled, and the soil of parcel 2 was prepared for cereal cropping. Then, the analysis of variance has been applied on the differences of TS and RTK GPS elevations data to estimate the confidence interval of ground control points elevation due to soil tilth, whereas the times series statistical method has been applied on elevation data to estimate the confidence interval due to soil roughness. The confidence intervals of points elevation are estimated being [51 mm; 57 mm], [-4 mm; 4 mm] for parcel 1, and [97 mm; 113 mm], [-35 mm; 23 mm], for parcel 2. Results show that ground control point's elevations exactness is influenced by soil tilth and soil roughness. In conclusion, we can admit that soil tilth and soil roughness have significant impact on the exactness of ground control points located on agricultural parcels. This impact must be considered in Digital Elevation Model (DEM) errors evaluation of agricultural watershed.

Table des matières

1. Introduction

1Ces dernières années, l'intérêt croissant des scientifiques par rapport à la qualité des résultats fournis par les modèles mathématiques s'est marqué par de nombreuses recherches et publications. Particulièrement, dans le domaine de l'hydrologie et de l'hydraulique, plusieurs questions se posent sur la qualité des résultats des nombreuses applications qui font appel aux Modèles Numériques de Terrain (MNT). Le MNT est une représentation numérique et mathématique de l'altitude d'un point quelconque de la surface terrestre d'une zone géographique, dans un système référentiel bien défini. Selon Carter (1988), un MNT, même de meilleure exactitude, reste une approximation de la réalité du terrain. Dès lors, il contient toujours des erreurs.

2Les sources d'erreurs du MNT sont variées et incluent principalement :

3– l'exactitude des points de contrôle¹,

4– leur densité²,

5– la distribution des données sources³,

6– la situation géographique de la zone d'étude⁴,

7– les méthodes d'interpolation utilisées pour générer le MNT⁵,

8– la microtopographie de la zone d'étude⁶

9(Li, 1991 ; Zhou et al., 2002 ; Zhu et al., 2005 ; Heritage et al., 2009).

10Huang et al. (2005) et Oksanen et al. (2005) ont montré que ces erreurs peuvent se propager et influencer considérablement les résultats finaux d'une application.

11L'Écart Quadratique Moyen (EQM) est le paramètre statistique utilisé par plusieurs auteurs (Li, 1992 ; Desmet, 1996 ; Chaplot et al., 2006 ; Liu et al., 2008 ; Bater et al., 2009 ; Höhle et al., 2009 ; Chen et al., 2010) pour quantifier l'exactitude du MNT. Pour calculer l'EQM d'un MNT, il est nécessaire de disposer de points de contrôle dont l'exactitude des coordonnées est significativement meilleure que celle des données originales qui seront utilisées pour générer le MNT (Wechsler, 2007). Li (1991 ; 1992) a montré que l'exactitude d'un MNT est influencée par la densité, la précision et la distribution des points de contrôle. Peu d'études ont été menées concernant l'influence de la microtopographie sur l'exactitude des MNT. La microtopographie des parcelles agricoles étant en perpétuel changement, elle pourrait avoir un impact non négligeable sur l'exactitude de l'élévation des points de contrôle. Sur les parcelles agricoles, le travail du sol vise principalement à créer des conditions de croissance et de production favorables pour la plante. Les principaux objectifs sont dès lors de créer un volume de pores suffisant pour absorber l'eau et l'air et pour permettre une pénétration facile des racines des plantes en ameublissant le sol dans la couche cultivable. Pendant cette opération, et selon la culture à semer, la rugosité de la surface de la parcelle est modifiée ainsi que son état d'ameublissement.

12Plusieurs études ont été menées dans l'objectif de caractériser la rugosité de la surface des sols, car il est admis par plusieurs auteurs que la rugosité est un paramètre important pour comprendre le mécanisme de l'érosion et du transport des sédiments, ainsi que le ruissellement à l'échelle de la microtopographie. C'est ainsi que Cerdan et al. (2001) mettent en évidence les trois variables à l'échelle de la microtopographie, dont les rôles sont prépondérants sur le ruissellement et la charge solide : la rugosité, la couverture végétale et le faciès (stade de développement de la croute de battance). Le Bissonnais et al. (2004) ont quant à eux défini à partir de mesures visuelles de la rugosité et du faciès, six états de surface déduits de la grande diversité de techniques culturales.

13Dans la littérature, les méthodes utilisées pour mesurer la rugosité d'une surface sont classées en deux catégories : les méthodes nécessitant un contact direct avec la surface expérimentale dont la méthode du profilographe (Kuipers, 1957 ; Podmore et al., 1981), la méthode de la chaine (Saleh, 1993 ; Merrill, 1998) et la méthode du rugosimètre électronique (Planchon et al., 1998) ; et les méthodes utilisant les techniques de la télédétection dont la photogrammétrie, le laser (Römkens et al., 1986 ; Huang et al., 1988 ; Bertuzzi et al., 1990 ; Jester et al., 2005) et les méthodes acoustiques (Oelze et al., 2003).

14En général, une analyse approfondie de la rugosité du sol nécessite des mesures en 3D de la topographie, ce qui demande une mise en place assez lourde. Cependant, il est parfois nécessaire de pouvoir caractériser la rugosité à partir de moyens de mesure simples en 2D à travers des paramètres simples. L'utilisation du profilographe sur des transects reste la plus fréquente en 2D à cause de sa simplicité. Cependant, cette technique présente le désavantage d'être destructrice au contact du sol (Moreno et al., 2008).

15Des paramètres sont utilisés pour caractériser la rugosité. Il s'agit de  :

16– l'écart relatif entre la longueur d'une chaine déployée sur le sol et celle de sa projection sur un axe horizontal (dans le cas d'un profil linéaire issu d'un profilographe),

17– l'écart-type des altitudes minorées des effets de la tendance générale due à la topographie du sol,

18– la différence entre les valeurs maximale et minimale des altitudes mesurées sur un transect.

19Cependant, ces paramètres ne tiennent pas compte des erreurs aléatoires inévitables survenant pendant l'utilisation des matériels d'acquisition des données. Jester et al. (2005) ont seulement abordé la résolution maximale atteignable par les différentes méthodes, ainsi que leur précision. Or pour une méthode de mesure, la rugosité peut être amplifiée par la présence d'erreurs aléatoires de mesure.

20L'acquisition des points de contrôle étant l'étape nécessaire pour estimer l'exactitude d'un MNT, il nous semble logique d'évaluer a priori l'influence de la microtopographie sur l'altitude des points de contrôle, ce qui permettra dans nos futures recherches d'analyser l'impact de la microtopographie sur l'exactitude des MNT.

21Notre objectif dans cet article est d'utiliser des outils statistiques afin de quantifier à travers des intervalles de variation des altitudes, d'une part l'influence de l'état d'ameublissement du sol d'une parcelle agricole, et d'autre part l'influence de son état de rugosité sur l'exactitude de l'altitude des points de contrôle positionnés au GPS. La méthode que nous utilisons pour estimer la rugosité est basée sur l'approche de la décomposition des données en série chronologique. Cette méthode permet l'analyse des données expérimentales minorées des erreurs aléatoires et permet de révéler le caractère répétitif de la rugosité des surfaces agricoles due à l'utilisation des outils de travail.

22Pour un point de contrôle donné, l'objectif est de pouvoir simuler indépendamment les erreurs dues d'une part à l'état d'ameublissement, et d'autre part à la rugosité du sol, erreurs qui, additionnées à l'altitude originale obtenue au GPS, génèrent une réalisation possible de cette dernière. Cette procédure nous assure de tenir compte de l'influence de la microtopographie sur l'altitude des points de contrôle pour l'évaluation de l'exactitude des MNT dans des études futures.

2. Matériel et méthodes

2.1. Caractéristiques des parcelles d'étude

23Deux parcelles agricoles ont été sélectionnées. Chaque parcelle a subi un travail du sol particulier. Le tableau 1 donne des informations sur les caractéristiques de ces parcelles.

2.2. Échantillonnage par levés GPS (Global Positioning System) et à la Station Totale (ST)

24Le récepteur GPS utilisé est un récepteur de précision centimétrique manipulé en mode RTK (Real Time Kinematic), recevant des corrections en temps réel par téléphone portable, émises par le système Walcors. Ce dernier est un réseau permanent de stations de référence couvrant le territoire de la Wallonie (Belgique) et appartenant à la Région wallonne (Walcors, 2007).

25La ST utilisée intègre une antenne GPS permettant de réaliser des levés GPS en mode RTK de points quelconques pouvant être utilisés comme points de référence pour la mise en station de l'appareil. Elle est également dotée d'un rayon laser qui permet à l'opérateur de lever un point avec une précision millimétrique sans y stationner un réflecteur. Cette opération permet de ne pas modifier l'altitude du point après l'opération de visée.

26Sur chaque parcelle expérimentale, trois transects ont été sélectionnés de manière aléatoire, mais perpendiculairement à la direction de travail du sol. Sur chaque transect, 16 points positionnés à un intervalle de 100 mm ont été levés (détermination des coordonnées x, y et z) d'abord à la ST, puis au GPS en mode RTK. Cette procédure expérimentale évite de modifier l'altitude du point à lever par la ST, ce qui permet d'obtenir l'altitude réelle du point sur le terrain. Cela n'est pas le cas pour le levé au GPS qui modifie la topographie du point par le fait de stationner la canne de l'antenne du GPS sur ce dernier. Dans la suite de notre travail nous nous référerons à T¹₁, T¹₂, T¹₃ pour désigner les trois transects sur la parcelle 1 et par T²₁, T²₂, T²₃ pour désigner les trois transects sur la parcelle 2.

2.3. Influence de l'état d'ameublissement des parcelles sur les points de contrôle

27Une analyse de la variance (AV) à deux critères de classification est appliquée sur les écarts d'altitude observés par les deux appareils dans le but d'estimer les erreurs accidentelles et les erreurs systématiques éventuelles introduites par le processus de mesurage de l'altitude des points de contrôle. Le sol de la parcelle étant ameubli par le travail du sol, l'altitude réelle mesurée au GPS est sous-estimée parce que la canne de l'antenne a tendance à s'enfoncer dans le sol. Ce qui n'est pas le cas de la ST qui mesure l'altitude réelle du point positionné en utilisant un rayon laser. Cela évite à l'opérateur de stationner un réflecteur sur le point.

28Les deux critères de classifications utilisés dans l'analyse de la variance sont :

29– le critère « Parcelle », considéré comme fixe,

30– le critère « Transect » considéré comme aléatoire.

31Selon Dagnelie (2006), le modèle statistique qui lie les deux critères de classification est le modèle mixte hiérarchisé, car les transects sélectionnés dans la parcelle 1 n'ont aucune correspondance dans la parcelle 2.

32Le modèle mathématique de l'analyse de la variance appliquée sur les écarts d'altitude s'écrit comme suit :

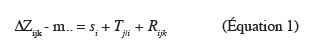
33où ∆Z_ijk est l'écart d'altitude sur le point k, observé sur le transect j de la parcelle i, m.. est la moyenne générale des écarts d'altitude observés sur tous les j transects de l'ensemble des i parcelles, s_i est la constante décrivant l'effet principal de la parcelle i sur les écarts d'altitudes observés, T_j|i est la composante aléatoire de l'effet du transect j dans la parcelle i, R_ijk comprend toutes les composantes aléatoires de l'erreur accidentelle qui ne sont liées ni à la parcelle, ni au transect.

34Si nous notons m_1., m_2. les moyennes des écarts d'altitude observés sur les parcelles 1 et 2,

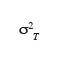la variance de la composante de l'erreur accidentelle liée au transect, les hypothèses nulles testées par l'analyse de la variance sont :

35Si l'hypothèse nulle H₀ est acceptée, cela signifie qu'il existe une égalité entre les moyennes des écarts d'altitude observés sur les deux parcelles.

36Si l'hypothèse nulle H₀^' est acceptée, cela signifie qu'il n'existe pas de différence significative entre les moyennes des écarts d'altitude observés sur les transects dans les deux parcelles.

37Le tableau 2 donne le tableau de l'analyse de la variance à deux critères (AV2) de classification pour un modèle hiérarchisé mixte.

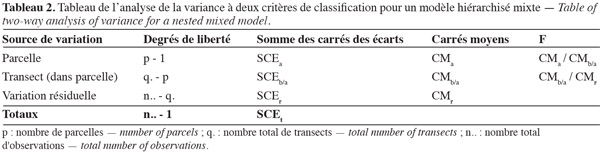
38Il existe un effet significatif d'un facteur si la valeur de F calculée est supérieure à la valeur critique de la variable de Fisher-Snedecor.

39L'analyse de la variance suppose que les distributions de probabilité des écarts d'altitude suivent une distribution normale et que leurs dispersions sont identiques d'une surface à l'autre, et d'un transect à l'autre. L'hypothèse de normalité des erreurs accidentelles liées au processus de mesurage des coordonnées d'un point par GPS est habituellement admise (Debouche et al., 2008). Cependant, l'analyse de la variance porte dans notre cas sur des différences d'altitude et non sur des altitudes. Néanmoins, nous pouvons conclure que la normalité des différences d'altitude découle de celle des erreurs de mesures sur les altitudes. Soulignons que l'analyse de la variance est relativement robuste vis-à-vis d'une éventuelle non-normalité des erreurs accidentelles, pour autant que la distribution soit une distribution en cloche (Dagnelie, 2006).

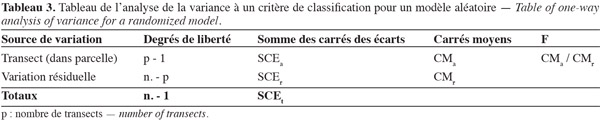
40Si l'une des hypothèses nulles de l'AV2 est rejetée, l'estimation de l'erreur accidentelle due au processus de mesurage de l'altitude des points de contrôle sur les parcelles devra se faire pour chaque parcelle en utilisant le modèle aléatoire de l'analyse de la variance à un critère de classification (AV1). Le tableau 3 donne le tableau de l'AV1 pour un modèle aléatoire.

41L'hypothèse nulle testée par l'AV1 pour la surface i est

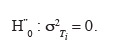
42Si l'hypothèse nulle H^"₀ est rejetée, cela signifie qu'il existe une différence significative entre les écarts d'altitude observés sur les transects de la parcelle i ; dans ce cas, l'écart-type estimé qui caractérise la variabilité des écarts d'altitude est donné comme suit :

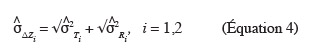
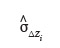est l'écart-type estimé qui caractérise la variabilité des écarts d'altitude dans la parcelle i,

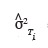est la composante aléatoire de l'effet du transect dans la parcelle i,

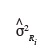est la composante aléatoire résiduelle des écarts d'altitude dans la parcelle i.

43Si l'hypothèse nulle H^"₀ est acceptée, l'écart-type estimé se déduit de l'équation suivante :

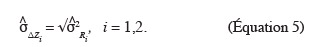
44Si les hypothèses nulles de l'AV2 sont acceptées, l'écart-type estimé caractérisant la variabilité des écarts d'altitude sur les surfaces 1 et 2 est donné par l'équation ci-dessous :

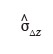est l'écart-type estimé qui caractérise la variabilité des écarts d'altitude sur les parcelles 1 et 2,

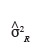est la variance résiduelle des écarts d'altitude observés dans les parcelles 1 et 2.

45Avec :

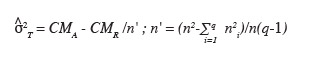
46il vaut l'effectif commun des trois transects si ces derniers sont de même effectif ;

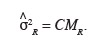
47Dans le cas où l'hypothèse nulle H^'₀ est rejetée, un test d'égalité de la variance permet de se prononcer sur l'égalité de la variabilité des écarts d'altitude observés sur les parcelles 1 et 2. Le test réalisé est un test F de Fisher-Snedecor qui nécessite le calcul du rapport des deux variances

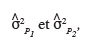
où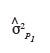

48est la composante aléatoire associée aux écarts d'altitude des points dans la parcelle P₁, et  

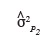
49est celle associée aux écarts d'altitude des points dans la parcelle P₂

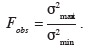
50Ce test suppose que les populations comparées sont indépendantes. L'hypothèse nulle est rejetée si la valeur de F_obs calculée est supérieure à la variable

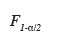de Fisher-Snedecor à k₁ et k₂ degrés de liberté, avec k₁ le degré de liberté (ddl) de la variance la plus grande et k₂ le ddl de la variance la plus petite (Dagnelie, 2006).

51Une fois la composante aléatoire des erreurs déterminée, la composante systématique peut être évaluée par un test de conformité qui permet de tester la nullité de la moyenne des écarts d'altitude observés (Debouche et al., 2008). L'hypothèse nulle testée est donnée par :

52Il s'agit du test t de Student qui compare la valeur de

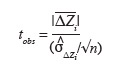
avec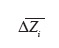

53la moyenne des écarts d'altitude observés sur la parcelle i,

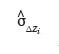l'écart-type estimé des écarts d'altitude observés sur la parcelle i, et n le nombre des écarts d'altitude observés,

54à la valeur de la variable t de Student à n-1 ddl. L'hypothèse nulle est rejetée au niveau de signification α si t_obs est supérieure à

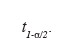
55L'intervalle de confiance qui contient les écarts d'altitude avec la probabilité peut être déduit de la formule ci-dessous :

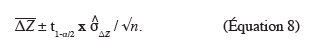
2.4. Influence de l'état de rugosité de la parcelle sur les points de contrôle

56Nous acceptons l'hypothèse que le modèle mathématique qui décrit les séries des altitudes observées à la ST sur un transect j est additif. Si le transect j est composé de p périodes, le modèle mathématique est donné par l'équation suivante :

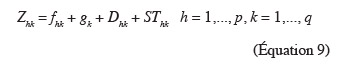
57où q désigne le nombre d'observations altimétriques localisées sur une période h. La valeur de q a été déterminée grâce à la connaissance des dimensions des outils de travail du sol pour le labour et le semis, et en observant les traces laissées sur les transects pendant les mesures. Cela permet aisément de compter le nombre de points localisés sur une période. Ces observations montrent que q vaut 3 pour la parcelle 1 et 5 pour la parcelle 2. Le choix de ces valeurs a été confirmé en testant le caractère aléatoire des résidus a posteriori ; f_hk est la tendance générale, c'est-à-dire dans notre cas, la pente du transect j. Elle peut être recherchée par les méthodes classiques de la régression, linéaire ou non ; g_k est la composante périodique qui se reproduit indéfiniment dans l'espace en restant toujours identique à elle-même. Elle peut être déterminée en calculant les écarts entre les valeurs observées z_hk et les valeurs correspondantes de la tendance générale

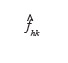
58comme indiqué dans l'équation ci-dessous :

59On définit ensuite les moyennes

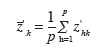
60et les écarts périodiques :

61Les valeurs observées des composantes aléatoires sont calculées par l'équation ci-dessous :

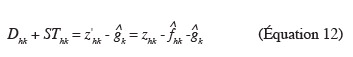
62D_hk est la composante aléatoire résiduelle dans le transect j due à la variabilité des altitudes ; ST_hk est la composante aléatoire dans le transect j due à l'appareil de mesure, une station totale dans notre cas.

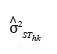est donnée par le constructeur de l'appareil dans le manuel technique qui accompagne ce dernier, elle est donc connue.

3. Résultats et discussion

3.1. Analyse des différences d'altitude

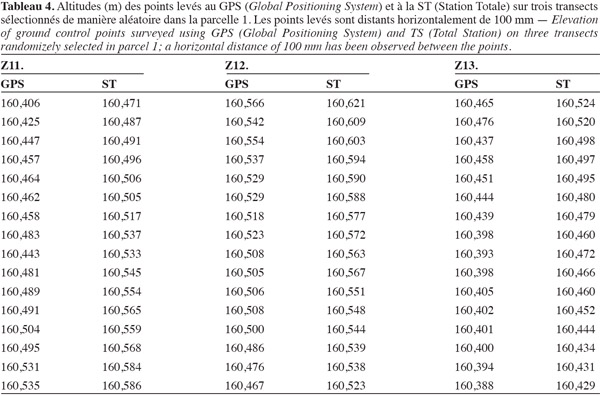
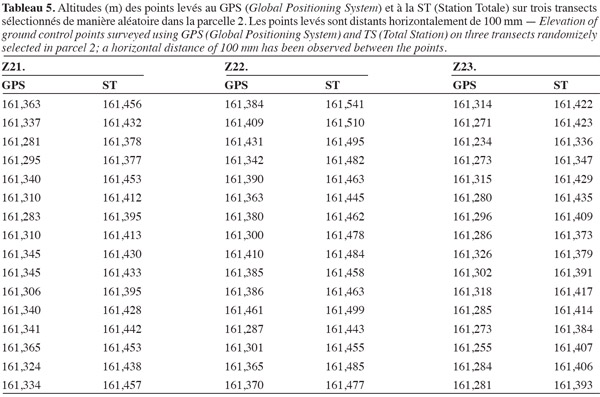
63Les tableaux 4 et 5 présentent les altitudes mesurées au GPS et à la ST sur les transects des parcelles 1 et 2.

64Le tableau 6 présente le résultat de l'analyse de la variance à deux critères de classification réalisée sur les écarts d'altitude. Nous pouvons remarquer que l'hypothèse d'égalité des moyennes des écarts d'altitude sur les deux parcelles est rejetée. Il existe donc une différence significative entre les moyennes des écarts d'altitudes observés sur les parcelles. Nous pouvons donc appliquer l'AV1 sur les écarts d'altitude observés séparément sur chacune des parcelles.

65Les tableaux 7 et 8 présentent les résultats de l'AV1 réalisée sur les écarts d'altitude observés sur les transects des parcelles 1 et 2 respectivement.

66Nous pouvons remarquer que l'hypothèse d'égalité de la moyenne des écarts d'altitude sur les transects de la parcelle 1 peut être acceptée car F est inférieure à la valeur critique de F à 2 et 45 degrés de liberté. Il n'y a donc pas de différence significative entre les moyennes des écarts d'altitude d'un transect à l'autre dans la parcelle 1. La même conclusion peut être tirée des résultats du tableau 8. Le calcul des écarts-types, qui caractérisent la variabilité des écarts d'altitude, peut être réalisé en utilisant l'équation 5.

67Le tableau 9 présente les composantes de la variance accidentelle liée à la variabilité des écarts d'altitude observés dans les parcelles 1 et 2.

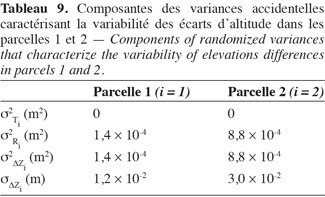
68Nous pouvons maintenant nous prononcer sur l'égalité de la variabilité des écarts d'altitude dans les parcelles 1 et 2.

69La valeur de

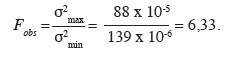
70Cette valeur est supérieure à la valeur F_0,975 à 45 et 45 degrés de liberté 1,82. Nous pouvons donc conclure au rejet de l'hypothèse nulle d'égalité des variances. Il existe une différence significative entre les variabilités des écarts d'altitude dans les parcelles 1 et 2.

71L'estimation des variances accidentelles permet de nous prononcer sur la justesse du positionnement des points de contrôle par GPS. Les moyennes des écarts d'altitude pour les parcelles 1 et 2 valent respectivement 50 mm et 110 mm.

72Le tableau 10 résume les résultats des tests de conformité de la moyenne des écarts d'altitude réalisés. Nous pouvons constater que les hypothèses nulles sont rejetées. Les moyennes des écarts d'altitude observés sont significativement différentes de zéro pour les deux parcelles. Nous pouvons en conclure que l'influence de l'état d'ameublissement du sol des parcelles sur l'altitude des points de contrôle n'est pas insignifiante. Les altitudes des points de contrôle sont donc sous-estimées lors de la mesure au GPS. Pour les corriger, nous devons leur sommer les écarts d'altitude qui seront déterminés dans les intervalles indiqués dans le tableau 11 selon une distribution normale (puisqu'il a été admis dans le § 2.3. que les distributions de probabilité des écarts d'altitude suivent une loi normale) dont la moyenne et l'écart-type sont connus pour chaque parcelle.

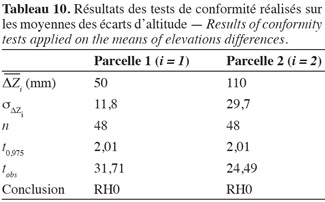
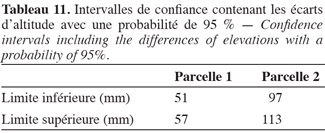
73Le tableau 11 indique les intervalles de confiance qui contiennent les écarts d'altitude avec une probabilité de 95 %.

3.2. Analyse des variations d'altitude

74Le tableau 12 synthétise les résultats de la décomposition des séries chronologiques composées des altitudes observées à la ST sur les transects des parcelles 1 et 2. Les données ont été analysées à l'aide du logiciel statistique Minitab⁷.

75Nous pouvons remarquer une variation de la composante périodique des séries chronologiques des altitudes observées, dans les intervalles [-3 mm ; 3 mm] et [-29 mm ; 17 mm] respectivement pour les parcelles 1 et 2. Nous pouvons a priori en déduire que ces intervalles peuvent être utilisés pour caractériser les intervalles de variation des altitudes des points de contrôle sur les parcelles. Cette variation est une conséquence de la rugosité de la surface des parcelles, mais également des erreurs aléatoires inévitables dues au matériel de mesurage, c'est-à-dire des erreurs aléatoires propres à la ST.

76La longueur de l'intervalle, c'est-à-dire la différence entre sa borne supérieure et inférieure est de 6 mm pour la parcelle 1 et de 46 mm pour la parcelle 2. Cependant, nous devons tenir compte de l'influence des erreurs aléatoires sur les intervalles de variation.

77Nous acceptons l'hypothèse que les distributions de probabilité des erreurs aléatoires sur les altitudes obtenues sur chaque transect, après décomposition des séries des altitudes observées, suivent une distribution normale. Dans ce cas, nous pouvons nous prononcer sur l'égalité de la variabilité des erreurs aléatoires de mesure des altitudes sur les transects sélectionnés dans les parcelles en réalisant une analyse de la variance à un critère de classification. L'hypothèse nulle testée est la nullité de la variabilité des erreurs aléatoires d'un transect à l'autre

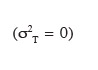
78dans une même parcelle. Le tableau 13 montre les résultats des analyses de variance réalisées. Nous pouvons accepter l'hypothèse nulle pour les parcelles 1 et 2.

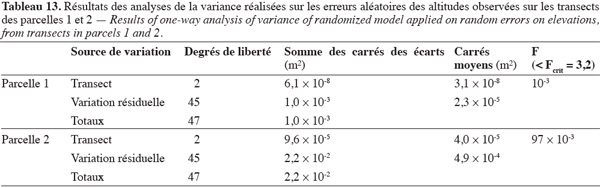
79Dans une même parcelle, la variabilité des erreurs aléatoires sur les altitudes observées peut ainsi se déduire du carré moyen résiduel. Nous obtenons respectivement, pour les parcelles 1 et 2, des écarts-types valant 5 mm et 22 mm.

80Le tableau 14 donne des estimations des intervalles de confiance (intervalle contenant les altitudes avec une probabilité de 95 %) des écarts d'altitudes autour des valeurs minimale et maximale de la composante périodique des altitudes sur les transects des parcelles 1 et 2 en tenant compte des erreurs aléatoires.

81Nous pouvons remarquer que les composantes périodiques sont dans les intervalles [-4 mm ; +4 mm] et [-35 mm ; +23 mm] respectivement pour les parcelles 1 et 2, avec une probabilité de 95 %. Ces intervalles nous montrent qu'il existe une incertitude sur l'altitude des points de contrôle. Cette incertitude est la cause de la rugosité des parcelles due à l'utilisation des outils de travail. Cependant, cette rugosité diffère selon l'état de surface de la parcelle. La rugosité semble moins importante dans la parcelle 1. En effet, la longueur d'intervalle, c'est-à-dire la différence entre les bornes supérieure et inférieure est de 8 mm dans la parcelle 1, et de 58 mm dans la parcelle 2, c'est-à-dire 7 fois plus importante. Cela nous semble normal car pendant le semis des céréales, le travail du sol reste surtout superficiel.

82Des réalisations possibles des altitudes des points de contrôle peuvent être obtenues en additionnant aux altitudes mesurées au GPS, des erreurs déterminées selon une loi uniforme dans les intervalles ci-dessus, car pour un intervalle donné, toutes les valeurs (situées dans l'intervalle) ont la même probabilité d'être sélectionnées.

83L'étude de Le Bissonnais et al. (2004) a permis d'établir, à partir d'observations visuelles, un tableau de classification permettant de déterminer pour les principales techniques de travail du sol, la rugosité, observée perpendiculairement (+) et parallèlement (//) à la direction de travail du sol. Pour des parcelles dont le travail du sol est un labour d'hiver, leurs résultats montrent une rugosité + (différence entre l'altitude minimale et l'altitude maximale d'un transect) variant entre 50 et 100 mm, c'est-à-dire une rugosité moyenne de 75 mm. Pour des parcelles dont le sol est travaillé pour le semis d'une céréale d'hiver, la rugosité varie entre 10 et 20 mm, c'est-à-dire une valeur moyenne de 15 mm.

84Comme nous pouvons le remarquer, la longueur de l'intervalle de variation de la composante périodique dans la parcelle 1, si l'on tient compte des erreurs aléatoires, vaut 8 mm. Elle vaut 58 mm pour la parcelle 2. Il faut noter que dans leur étude, Le Bissonnais et al. (2004) ont observé la rugosité sur des parcelles agricoles dont la couverture végétale et le faciès ne sont pas insignifiants, ce qui n'est pas le cas dans nos parcelles 1 et 2, qui étaient complètement nues avec un faciès inexistant. Nos résultats ne tiennent donc pas compte de l'interaction due à la couverture végétale et au faciès, qui ont certainement tendance à augmenter la rugosité observée par Le Bissonnais et al. (2004). Vu les résultats proches de ceux obtenus par ces derniers, nous pouvons admettre que la méthode que nous proposons pour estimer la rugosité donne des résultats satisfaisants.

85La méthode que nous avons développée pour estimer la rugosité des parcelles 1 et 2 peut être un apport supplémentaire pour affiner le tableau de classification défini par Le Bissonnais et al. (2004), car d'une part cette méthode se base sur des données acquises à partir de matériels topographiques très précis, et non sur des observations visuelles qui peuvent varier d'un observateur à l'autre. D'autre part, cette méthode se base sur des analyses statistiques fiables et simples qui permettent de tenir compte de l'influence de la pente et des erreurs aléatoires sur l'altitude des points positionnés sur un transect.

4. Conclusion

86Dans cet article, nous avons présenté une méthode d'estimation de l'exactitude de l'altitude des points de contrôle localisés sur des parcelles agricoles. Nos résultats montrent que l'altitude des points de contrôle est influencée par l'état d'ameublissement du sol d'une part et d'autre part, par la rugosité de la surface des parcelles. Dans le cas des parcelles dont les sols ont été labourés (parcelle 1), et travaillés pour le semis de céréales (parcelle 2), des mesures GPS et ST nous ont permis d'estimer les intervalles qui contiennent d'une part les écarts d'altitude par rapport à l'altitude réelle d'un point de contrôle et d'autre part, les intervalles qui contiennent les variations de ces altitudes réelles du fait de l'aspect rugueux des surfaces agricoles. Dans le cas des parcelles 1 et 2, l'analyse de la variance nous a permis de déterminer l'intervalle qui contient les écarts d'altitude avec une probabilité de 95 %. Ces intervalles sont respectivement [+51 mm ; +57 mm] et [+97 mm ; +113 mm]. La fonction de distribution de probabilité des erreurs à l'intérieur de cet intervalle suit une loi normale. L'analyse statistique des séries chronologiques nous a permis de déterminer l'intervalle de variation de l'altitude. Les intervalles de variation sont respectivement pour les parcelles 1 et 2 de [-4 mm ; +4 mm] et [-35 mm ; +23 mm]. Cet intervalle est déterminé à partir de la composante périodique de l'altitude, qui suit une distribution uniforme.

87Pour un point de contrôle, des réalisations possibles de l'altitude, du fait de la présence d'erreurs dues à l'état d'ameublissement et à la rugosité du sol, peuvent être obtenues par simulation. Il suffit d'additionner aux altitudes obtenues au GPS, d'une part une erreur i (due à l'état d'ameublissement du sol) déterminée selon une loi normale, et une erreur ii (due à la rugosité du sol) déterminée selon une loi uniforme. Cette simulation permettra dans des études futures d'analyser l'influence de l'exactitude de l'altitude de ces points de contrôle sur l'exactitude des modèles numériques de terrain.

Bibliographie

Notes

Pour citer cet article

A propos de : Mohamar Moussa Ouédraogo

A propos de : Charles Debouche

A propos de : Aurore Degré