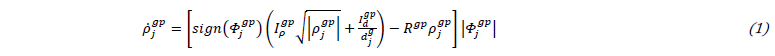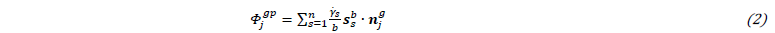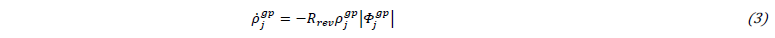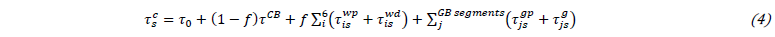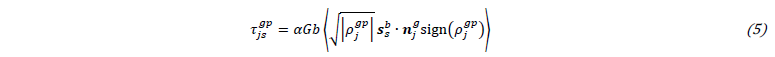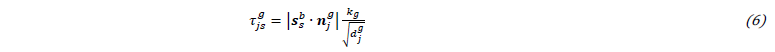1 Introduction

Bainitic high-strength low-alloy (HSLA) steels are widely used for the construction of pipelines for long-distance liquid and gas transport. The ability to control and predict pipe mechanical behavior is crucial to ensure their safe operation. However, the pronounced mechanical anisotropy of hot-rolled plates combined with the alteration of the mechanical response by pipe forming can seriously compromise pipe reliability. Yet, predicting the mechanical response of pipeline steel represents a significant challenge. It is above all the exceptionally strong Bauschinger effect, manifesting itself in HSLA steels as a yield stress reduction on reverse loading of up to 50% [1-3], that complicates the successful prediction of the pipe mechanical response.

Modern pipeline steels consist of different constituents, such as ferrite (polygonal, acicular, granular, bainitic), martensite-austenite, and non-metallic inclusions [2, 4-7]. These complex microstructures abound with obstacles, such as intragranular shear bands, homo- or heterophase boundaries, which in turn impede dislocation motion, leading to pile-up formation. The relatively easy release of dislocations from those pile-ups is generally considered as the main source of the Bauschinger effect upon load reversal.

Recent numerical studies have shown that state-of-the-art plasticity models have difficulties to accurately predict anisotropy evolution during pipe forming [1, 3]. This shortcoming applies to both advanced phenomenological models and dislocation-based models inspired by the intragranular substructure. Our previous work using the dislocation-based substructural hardening model by Peeters et al. [8] suggested that a faithful prediction of property evolution of bainitic pipeline steel in response to load path changes as they occur during pipe forming can be largely improved by accounting for ferrite interfaces [3].

The challenges lying ahead are two-fold: first, an accurate micro-scale hardening law is required. Dislocation-based models which explicitly include the dislocation substructure and pile-up formation are favored, since substructure and pile-ups are the major sources of the Bauschinger effect. This law is still to be developed and, based on our experience, should incorporate intragranular shear bands and grain boundaries as directional, planar glide obstacles including their crystallographic alignments. Second, once found, this novel law is to be embedded into a multi-scale simulation framework to address the materials' response to strain path changes for macroscopic simulations of pipe forming.

1.1 Dislocation-based hardening models for cubic materials

In the last 2 decades, several crystal plasticity-based models have been proposed for simulating the hardening response of plastic polycrystals subjected to simple or complex strain paths.

In line with the early derivations of Hall-Petch type strength and hardening contributions [9, 10], the model by Sinclair et al. [11] explicitly distinguished two hardening contributions due to dislocations accumulating at grain boundaries: (i) Taylor-type hardening due to the stored additional dislocation density and (ii) back stresses linked to specific (non-screened) configurations of excess dislocations. In contrast to strain gradient plasticity theories, this approach not only lifted the ambiguity of hardening due to “geometrically necessary dislocations” but also recognized the crucial role of their spatial arrangement.

An alternative continuum model was put forward by Rauch et al. based on the observation of massive dislocation annihilation in Al alloys and low carbon steels by reverse straining [12, 13]. The first model version divided the global dislocation population into two different types, labelled forward and reverse. The former type becomes activated by reverse shear and allows simulating work hardening for the special case of a reversed proportional strain path [12]. Later, this model was extended to cross-loading by introducing a third dislocation density and a parameter which measures the amplitude of the strain path change [13]. Kitayama et al. [14] reformulated that model within a crystallographic framework to incorporate slip directionality and texture effects. Instead of considering global dislocation densities, each slip system was associated with forward and reverse dislocations to allow for more general strain path changes. A similar, crystallographically-resolved approach was recently demonstrated by Bong et al. [15] for ferritic steel. In contrast, Carvalho Resende et al. [16] combined the earlier Rauch models with a grain-size dependent tensorial back-stress expression. In this way, they described plastic anisotropy and Bauschinger effect in IF steel for constant crystallographic texture.

When dislocations are not impeded by precipitates nor by grain boundaries, an intragranular dislocation substructure develops in bcc single-phase metals and alloys [17-19]. That substructure consists of randomly oriented cells and crystallographically oriented cell block boundaries (CBBs). In the model by Peeters et al. [8, 20], the substructural features in bcc materials are associated to three dislocation densities: 𝜌 (cells), 𝜌_𝑖^𝑤𝑑 (CBB on the i-th {110} plane) and 𝜌_𝑖^𝑤𝑝 (net dislocation pile-up at CBB i). While the pile-ups polarize the CBBs and cause reverse (Bauschinger) effects upon strain reversal, the CBBs give rise to latent hardening and cross-effects. Each slip system exhibits thus a different critical shear stress, which furthermore depends on the shear direction. In addition, the model considers that upon reloading, the previously developed cell substructure disintegrates, leading to a plateau on the stress–strain curve (hardening-stagnation). Integrated into the relaxed-constraint grain-interaction crystal plasticity framework ALAMEL [21], the Peeters model has successfully predicted the stress evolution during complex strain path changes and drawing operations for coarse-grained IF steels [22].

1.2 Present work

Despite the success of Peeters' model, our recent work suggested that incorporation of dislocation interactions with phase and/or grain boundaries are important to reliably reproduce the large Bauschinger effect exhibited by X70 pipeline steels [3]. Dislocation-dislocation interactions alone could not explain the strong stress differentials upon load reversal. Advanced bainitic steels such as X70 exhibit fine microstructures with a ferrite grain size, the main constituent, of 1-15 μm. In contrast to the coarse-grained IF steel for which the Peeters model was originally developed, X70 steel is thus very rich in grain boundaries. In the present work, we develop equations that extend the original Peeters model to dislocation-grain boundary interactions. These interactions contribute to grain-size strengthening (Hall-Petch effect) as well as to the Bauschinger effect by the formation of dislocation pile-ups at the grain boundaries. The present work is thus an important step towards an improved material model for fine-grained bcc materials.

2 Model development

2.1 Incorporating grain boundaries into the Peeters model

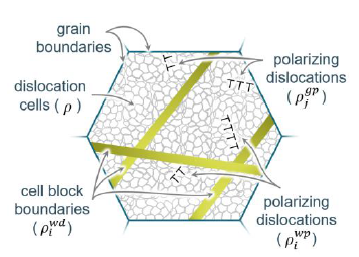
The model developed here schematizes the central features of the grain-boundary and dislocation substructure as illustrated in Fig. 1. Relative to Peeters' model it adds (i) straight grain boundary segments and (ii) for each grain boundary segment a new dislocation density 𝜌_𝑗^𝑔𝑝. 𝜌_𝑗^𝑔𝑝 represents dislocations piling up at a grain boundary and polarizing it.

Fig. 1: Schematic representation of the grain-boundary and dislocation substructure

In the following description we focus on the grain-boundary related features, while the remaining features are described in [8, 20]. Grain boundary pile-ups form by dislocation interaction with the grain boundaries and with other dislocations already accumulated there. On the other hand, interaction between dislocations accumulating on different slip systems may cause the destruction and screening of pile-ups. The following equation thus describes the accumulation of 𝜌_𝑗^𝑔𝑝 :

Note that 𝜌_𝑗^𝑔𝑝 can be > 0 or < 0 due to 𝛷_𝑗^𝑔𝑝, the net flux of dislocations onto the grain boundary:

with n the number of slip systems, 𝛾̇_𝑠 and 𝒔_𝑠^𝑏 the shear rate and slip direction for slip system s, 𝑏 the magnitude of the Burgers vector, and 𝒏_𝑗^𝑔 the grain boundary normal vector. The scalar product in (2) takes into account that the storage probability depends on the relative orientation of the incoming dislocation and the grain boundary. 𝐼_𝜌^𝑔𝑝 and 𝐼_𝑑^𝑔𝑝 are the storage parameters due to dislocation-dislocation and due to dislocation-grain-boundary interactions, respectively. 𝑑_𝑗^𝑔 is the distance between 2 grain boundary segments of orientation j. 𝑅^𝑔𝑝 characterizes the dynamic recovery in line with the Kocks-Mecking approach [23]. When the net flux for a grain boundary is reversed,

until 𝜌_𝑗^𝑔𝑝 changes sign. A change of sign of 𝜌_𝑗^𝑔𝑝 indicates that the net pile-up now forms on the other side of the grain boundary. The homogenized current critical resolved shear stress (CRSS) on slip system s is obtained by weighted summation of all relevant flow stress contributions:

^𝜏₀ is the Peierls stress, 𝑓 the volume fraction of CBBs, 𝜏^𝐶𝐵 the isotropic flow stress contribution from dislocation cells; 𝜏_𝑖𝑠^𝑤𝑝 represents the back-stress from pile-ups at CBB i, and 𝜏_𝑖𝑠^𝑤𝑑 is the contribution of the corresponding CBB itself. For each grain boundary segment, the second sum in (4) gathers the back-stress

and the grain-size strengthening

with 𝛼 characterizing the dislocation interaction strength, 𝐺 the shear modulus, and 𝑘_𝑔 the micro-scale Hall-Petch parameter. ⟨…⟩ in (4) indicates the Heaviside function

which lets dislocations escape from pile-ups without hindrance when the shear direction is reversed. This results in a lower flow stress and reduced hardening on reverse loading, i.e. a Bauschinger effect, as we will demonstrate in the next section.

2.2 Proof-of-concept

We now demonstrate that the equations introduced above in section 2.1 give rise to the desired stress-strain features including increased Bauschinger effect and grain size strengthening. For this purpose, we set up a hypothetical microstructure with one slip system 𝒔_𝑠^𝑏, one CBB 𝒏_𝑖^𝑤 and one grain boundary 𝒏_𝑗^𝑔:

Table 1 lists the values for the newly introduced model parameters for grain boundary features. For the storage and recovery rates for pile-ups at CBBs (𝐼^𝑤𝑝 and 𝑅^𝑤𝑝) and the remaining model parameters the values in [8] are used here. Disintegration of the random cell structure on load reversal by dislocations emitted from pile-ups at CBBs and at grain boundaries is neglected in the present setting.

Table 1. Grain boundary related model parameters

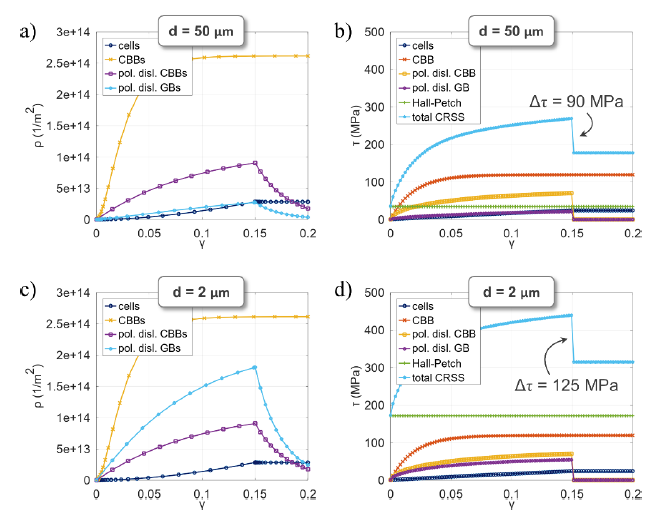
Fig. 2 shows the simulation results for forward shear of 0.15 followed by reverse shear for two different grain sizes, 𝑑_𝑗^𝑔= 50 μm and 𝑑_𝑗^𝑔= 2 μm. The calculated dislocation densities for cells, CBBs and pile-ups at CBBs are unaffected by the reduction in grain size. In contrast, the density of grain boundary pile-ups increases by more than 6 times when the grain boundary spacing decreases from 50 μm to 2 μm. The evolution of the CRSS shows a two-fold effect due to the reduction in grain size: (i) due to the Hall-Petch effect the overall stress-level increases by about 150 MPa and (ii) the stress differential due to reversal of the shear direction (γ = 0.15) is enlarged by 35 MPa. As clearly illustrated in Fig. 2(b) and 2(d), the origin for the enlarged Bauschinger effect is the larger flow stress contribution stemming from the polarizing dislocations piling up at grain boundaries in case of small grains.

Fig. 2: Evolution of (a,c) dislocation densities and of (b,d) critical resolved shear stress as a function of total shear strain for forward shear followed by reverse shear. Two different grain sizes are illustrated

3 Conclusions

The presented work demonstrates the development of a novel dislocation-based crystal plasticity hardening model for fine-grained bainitic steel. By building on the well-established approach by Peeters et al. [8, 20] to schematize the dislocation substructure in bcc materials, a model is obtained that demonstrably incorporates anisotropy from dislocation interactions with both CBBs and grain boundaries. By explicitly including grain size into the evolution equation for grain boundary pile-ups, two desired effects are achieved: (i) grain size (Hall-Petch-type) strengthening and (ii) an enlarged stress differential on reverting the strain path corresponding to an increased Bauschinger effect. Our experience has shown that both are required to accurately predict the stress response during complex strain-path changes occurring during pipe forming of bainitic steel plates. With respect to the practical application of the suggested model, reliable calibration of the model parameters might be challenging. As a remedy, a sequential design strategy for global optimization of black-box functions, as demonstrated previously [3], might be considered.

Acknowledgements

The authors would like to thank Philip Eyckens for insightful discussions on the crystal plasticity source code.