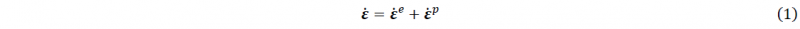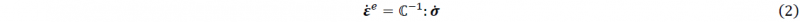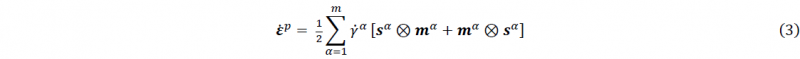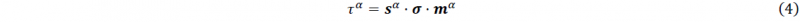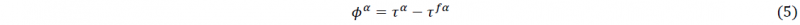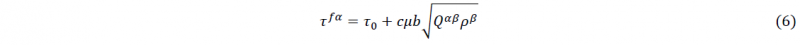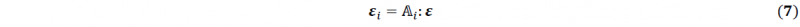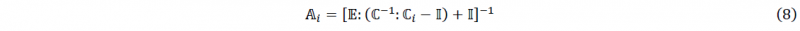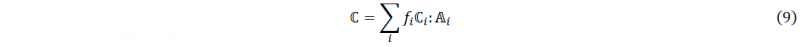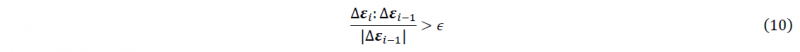1 Introduction

For metal forming simulations one of the important goals is to predict failure which in sheets mostly occur due to localized necking. It is known that the accuracy of the prediction of localized neck strongly depends on the ability of the yield function in representing the material behavior correctly. Furthermore, the behavior of the material usually depends on its plastic deformation history where strain path changes and the Bauschinger effect have a strong influence on the subsequent yield behavior. The aim of the current work is to provide an understanding on these dependencies using a multi-scale modeling approach known as the Mean-field homogenization framework.

Crystal plasticity-based modeling (CP) of the plastic deformation of metals has been the subject of many studies since it gives a direct relation between the microstructure and the observed macroscopic properties [1-3] which allows prediction of the yield locus as well as localization. There have been numerous studies for combining CP with the Finite Element method (FE) starting from a direct full-field approach where every integration point is assumed to lie in a crystal and the stress update is performed using CP [4]. The calculation of stresses can be performed using a visco-plastic or a rate-independent approach and in [5] a comparison of these can be found. In the current work, the CP implementation is based on a rate-independent approach [6,7].

Although the assumption is that all plastic deformation is inherently described by the CP models, the material itself is an aggregate of many crystals. Each of these crystals can be modeled as a single crystal in CP however the interaction of these must be considered to fully analyze the plastic behavior in macroscale. This requires a certain scale transition approach which can be carried out using the direct CP FE, but also analytical homogenization using the Mean-Field (MF) theory. In MF, all constituents of an aggregate are treated as individual phases and only their average behavior is taken into account [8]. The interaction between different phases is governed by Eshelby’s solution of the inhomogeneity problem [9]. The elastic-plastic extension of this theory has been provided in [10] and a Self-Consistent scheme is proposed to deal with the strain and stress partitioning in the constituent phases using MF [11,12]. More recently, the Viscoplastic Self-Consistent approach (VPSC) has been used to directly obtain FE simulation of forming operations [13].

In the following, first the modeling approach that is used for Crystal Plasticity as well as the Self-Consistent Mean Field homogenization framework are summarized. The results of the material point simulations are presented next to be followed by conclusions.

2 Modeling

2.1 Crystal Plasticity

In this section a summary for the small strain Crystal plasticity algorithm is given, more details of this and the large deformation theory and implementation can be found in [6,7]. Starting from the additive decomposition of the symmetric part of rate of deformation gradient ̇H =𝛁𝒖̇ into elastic and inelastic parts one obtains:

where

and

with ℂ, fourth order the elasticity tensor, s^α and m^α the slip direction and the slip plane normal to the active slip system α, respectively, 𝛾̇ the slip rate and m the number of active slip systems. For slip activity to occur on a slip system the resolved shear stress on that system given by

must be equal to the critically resolved shear stress, 𝜏^𝑓𝛼 on that system. This results in the flow rule for that slip system:

In the applied framework the hardening on each slip system is governed as a function of the dislocation density in the following form:

with 𝜏₀ as the initial slip resistance (constant for all slip systems), c the Taylor factor, μ the shear modulus, b the Burgers vector and Q the hardening matrix.

The solution of the above equations has been previously carried out successfully using a rate independent scheme by means of an optimization algorithm using Lagrange multipliers which imposes the flow rule for each active system as a constraint equation while maximizing the plastic dissipation [5,6,7]. However, using this scheme generates convergence problems in the homogenization algorithm due to non-differentiability at the elastic-plastic transition. To circumvent this the Lagrangian optimization algorithm has been replaced with an Interior Point based optimization algorithm [14] which ensures that the transition remain differentiable.

In this method the constraints, i.e. flow rule for each slip system, are ensured to be satisfied without the requirement for a return-mapping algorithm as the stress never violates these conditions and during iterations always remains in the elastic domain. When the stress reaches the yield point the amount of slip as well as the hardening are calculated using the consistency condition. This algorithm above also enables calculation of an algorithmic tangent analytically which is used in the homogenization algorithm without the need for a numerical perturbation as in [14].

2.2 Self-consistent Homogenization

Homogenization of the behavior of the polycrystal aggregate is carried out using the Mean-Field method. In this method an imaginary RVE is assumed in which the inhomogeneity is introduced. The inhomogeneity problem is solved analytically, and the results are transferred to macroscale representing the averaged behavior of the material point. Depending on how the solution is performed and the assumptions therein different homogenization schemes are obtained.

In this work the Self-Consistent scheme is utilized. In the Mean-Field method the main problem can be reduced to finding strain concentration tensors for each phase (crystal) in the following form:

where 𝔸 is the fourth order strain concentration tensor. In the Voigt (iso-strain) scheme the strain concentration tensor is equal to fourth order unit tensor, which is also referred to as the Taylor scheme when an RVE of each phase is solved separately with the boundary conditions that create the same strain in every crystal.

In the Mean-Field approach Eshelby’s solution of the inhomogeneity problem is used to get an approximation of the strain concentration tensor which results in the following expression:

where 𝔼 is the fourth order Eshelby tensor, 𝕀 is the fourth order unit tensor, ℂ_i is the material tangent for phase i and ℂ is the homogenized material tangent of the aggregate given by:

with f the volume fraction of each phase. The details of the theory and the implemented algorithm can be found in [8].

3 Results

3.1 Material parameters

For the simulations an imaginary, Aluminum-like material is considered. The crystals therefore have an fcc type lattice structure with the hardening function given in Eq. (6). The properties assigned to each crystal are tabulated in Table 1. What remains are the three Euler angles per crystal which are chosen from a random rotation matrix generated using (scipy.stats.special_ortho_group) the SciPy Python-based scientific computing software [15].

Table 1. Material parameters used in CP.

3.2 Crystal Plasticity Finite Elements comparison

For validating the implemented Self-Consistent Crystal Plasticity approach, first a comparison with a full-field simulation is performed. For this simulation, the crystal plasticity algorithm is implemented as a user sub-routine (UMAT) to the commercial finite element software ABAQUS. The code that performs stress-update for the non-linear solution scheme in UMAT is the same as the one that returns stresses and the material tangent for the homogenization algorithm.

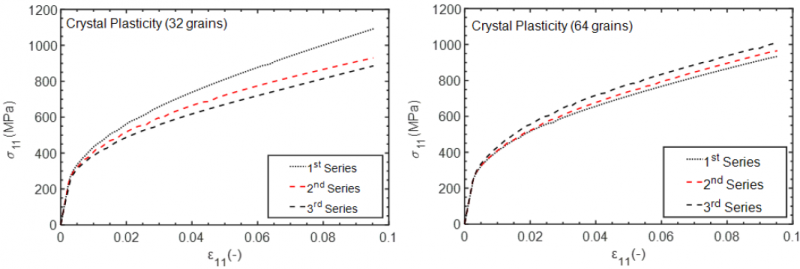
As a reference simulation a 2D RVE with periodic boundary conditions and plane-strain condition is generated. Each grain is represented by a hexagonal geometry. Every grain is assigned a certain initial crystal orientation and the RVE is loaded in the horizontal direction as shown in Fig. 1.

Fig. 1. RVE made up of 32 hexagonal grains.

For the comparison, 32 and 64 grain simulations are used which have been run with 3 different sets of orientations, to represent reproducibility of the results. It is observed based on the results shown in Fig. 2. that 32 grains are not representative enough to capture the behavior of the crystal whereas 64 grains are acceptable.

Fig. 2. Full-field crystal plasticity finite element simulation results of the RVE.

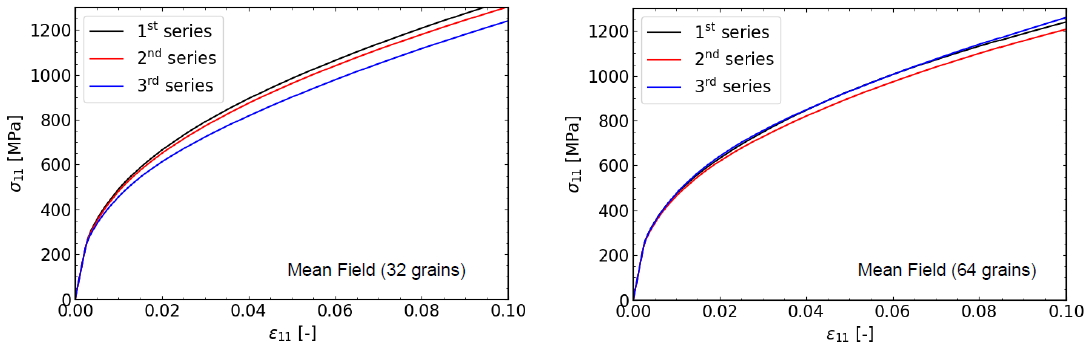Fig. 3. Mean-Field crystal plasticity results of the polycrystal aggregate.

In Fig. 3. the results of the Self-Consistent crystal plasticity algorithm are shown. Although the general trend seems similar the actual hardening curves are different than those obtained by the full-field simulations. There are several important differences in the two simulations which are relevant in putting these differences into perspective. The first difference is that the full-field FE simulation is plane-strain. That implies that at all integration points, the material experiences vanishing thickness strains. This in the end results in an average zero thickness strain. However, in the MF approach only the average of all crystals has a vanishing thickness strain. This means that individual crystals can have non-zero thickness strains. The second important factor to consider is that the behavior of each crystal in the full-field FE simulation is influenced by the neighboring crystals, defined by the misorientation relation. This can also explain the higher variations of the behavior with different grain orientation distributions. On the other hand, in the MF approach the misorientation does not play a role. All crystals are assumed to be surrounded by a homogeneous material with the properties of the aggregate. This is believed to reduce the dependency on grain orientations.

3.3 Yield surface determination

The yield surface is defined at the points in stress space at which plastic deformation is observed. This definition can be directly applied to any algorithm where a single phase exists, and a certain flow rule is employed. In the Mean-Field approach (as well as the full-field simulation) however the observation of plastic deformation does not occur synchronously with slip activity on a single slip system. The amount of macroscopic plastic deformation associated with a single slip activity would be too small to cause any observable change in the flow curve. Therefore, in the determination of the yield surface instead of using algorithmically known slip amounts, the observed change in behavior is considered.

This is achieved by imposing specific stress increments on the material and observing the magnitude and the direction of the resulting strain increment:

When the difference in the scalar value obtained by projecting the new strain increment tensor on the previous one is larger than the previous scalar with a certain threshold yielding is assumed to have started. The underlying basis for this criterion is related to maximum dissipation principle where for the same given change in stress the strain direction and magnitude is significantly different in the elastic-plastic deformation regime than only elastic. Using the above algorithm, the plane-stress yield surface obtained by using 64 randomly generated orientations, with a threshold value 𝜖=0.0038, is shown in Fig. 4.

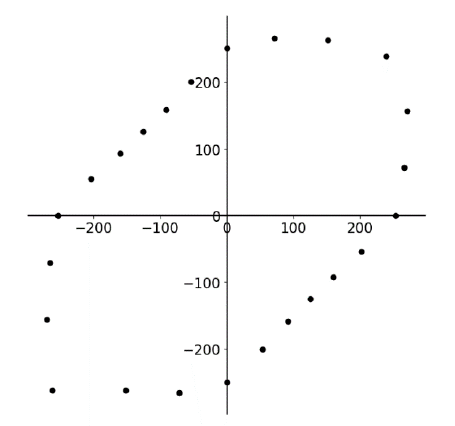Fig. 4. The plane-stress yield surface obtained using the Mean-Field homogenization of 64 random crystals.

It is observed that the shape of the yield surface shows local deviations and is not fully symmetric. The reason for this is attributed mainly to two factors. First is the limited number of orientations, 64, used for the generation of the data which gives statistical deviations from isotropy. The second factor is the chosen threshold as the yield criterion. The current implementation relies on user intervention for determining a fixed threshold, which causes deviations based on the stress direction.

3.4 Yield surface evolution

It is known that when after a certain amount of plastic deformation in a certain direction the loading direction changes the yield behavior of the material gets affected. The most extreme case, load reversal, manifests itself as the Bauschinger effect. In the implemented hardening rule for crystal plasticity there is no special treatment for load path changes, including the Bauschinger effect. Only a physically based hardening interaction matrix takes care of the cross-hardening behavior amongst the slip systems. In Fig. 5. a cyclic uniaxial loading of the material is shown.

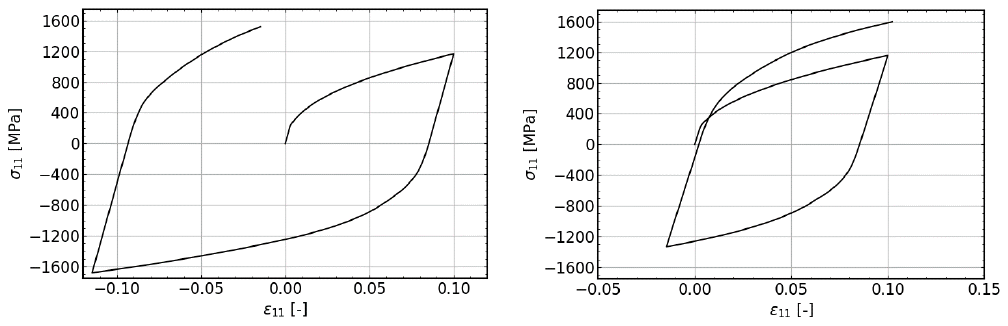Fig. 5. Cyclic uniaxial tension-compression results.

Clearly the model can capture the Bauschinger effect where early re-yielding is apparent. The smoothness of the reverse yield is also in line with experimental observations. The two different cycles also show that the magnitude of the effect is also plastic strain dependent. In the big loop, in the reverse direction, a plastic strain of 0.1 extra is imposed which results in approximately 400 MPa of extra stress in that direction. However, after reversal it can be seen that another strain of 0.1 in the forward direction keeps the magnitude of stress is in the same order. This result also supports the relation between anelastic deformation and the Bauschinger effect as discussed in [16].

4 Conclusions

A Self-Consistent Mean-Field homogenization algorithm is implemented where the individual behavior of each phase is modeled using a rate-independent crystal plasticity algorithm. This CP algorithm allows definition of a clear elastic-plastic transition and therefore an elastic domain which is essential in determining the yield behavior of a polycrystal aggregate.

The results of the MF approach are compared with a direct FE, full-field simulation where the same CP algorithm is used at the integration point level for stress update in the commercial FE software ABAQUS. The results differ significantly in terms of stress-strain behavior and the potential reasons for this are the treatment of the plane-strain assumption in each case and the effects of misorientation in the full-field simulation.

The yield surface of the aggregate is determined by analyzing the stress-strain behavior and considering the change in the strain increment obtained for a given specified stress increment between elastic and plastic deformation regimes. Although the obtained yield surface for 64 orientations looks reasonable, it is observed that the results are affected by numerical factors such as the number of orientations and the threshold value set by the user.

In case of cyclic uniaxial loading the model predicts the Bauschinger effect without explicitly adding a kinematic hardening term in the model. This implies that a significant part of the early re-yielding is caused by the inhomogeneity of the stress and strain distribution amongst the crystals.

Acknowledgements

The numerous discussions with Celal Soyarslan on yield point determination and yield behavior of metals are greatly acknowledged.