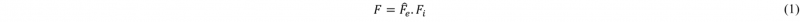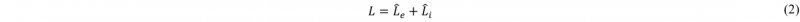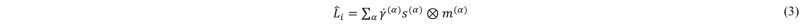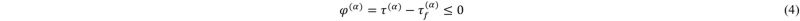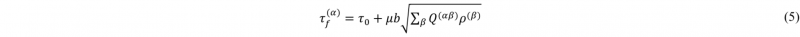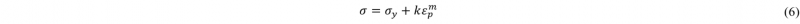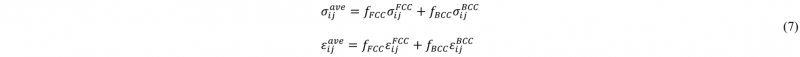1 Introduction

Heterogeneities that exist in materials at different scales, influence the way that material responds to mechanical loading. Hence, the necessity of a suitable method to represent heterogeneous microstructures is well recognized. Multiscale modeling is one of the most well-known tools to capture these effects at various scales and deduce macroscopic constitutive equations. Macroscale models have proved to be insufficient to represent material behavior and consequently multiscale methods act as a bridge by which it is possible to simultaneously switch to multiple scales. The connection between the macro and meso scales is possible via the concept of a Representative Volume Element (RVE). Although RVEs are widely applied to obtain material behavior efficiently, they are impractical to be adopted in finite element simulations of real forming processes.

Mean field method is one of the most efficient ways to simplify the behavior of high-dimensional stochastic models by means of approximating the original fields with averaging over degrees of freedom. This method is built upon the concept of an RVE in which an analytical evaluation of the problem, at a smaller scale, is replaced by a numerical solution [1]. There are several schemes in mean field method and regarding their fundamental presumptions for far field strain that is imposed on the RVE, they are employed for various problems [2]. Self-Consistent scheme is one of the most widely used ones for multiphase materials in which the inclusion is assumed to be embedded in a matrix with the homogenized elastic properties of the RVE [3]. Doghri and Friebel [4] investigated effective elasto-plastic properties of composites reinforced with inclusions taking into account inclusion shape, orientation and cyclic response. Doghri and Tinel [5] implemented the mean field homogenization of multiphase elasto-plastic materials that are reinforced with non-spherical and non-aligned inclusions.

In addition to mean field schemes, crystal plasticity models are applied extensively in understanding and estimating the evolution of the microstructure and associated anisotropic stress–strain response in polycrystalline metals which are exposed to large plastic strains [6,7]. In rate-independent crystal plasticity, unlike the rate-dependent theory, just some of slip systems are active which must be determined [8]. The investigations regarding the comparison between mean field and crystal plasticity method for a specific material are limited and in order to summarize one of the most relevant ones, Lebensohn et al [9] studied microstructure property relations for polycrystalline aggregates using two multiscale approaches: full-field versus homogenization methods. At one side, second-order viscoplastic self-consistent (VPSC) model was applied and on the other, the fast Fourier transform (FFT)-based formulation was used. It should be noted that in VPSC model, each grain is considered as an ellipsoidal inclusion interacting with a homogeneous effective medium. This method has been successfully used to express the mechanical response and crystallographic texture development during plastic deformation [10].

In this paper, macroscopic hardening for an arbitrary material composed of two phases (FCC and BCC) was obtained using two methods: crystal plasticity simulations of an RVE under tensile loading and mean field model. The aim of this study is to inspect the functionality and efficiency of mean field methods besides its limitations in prediction of a mixture behavior. Finite element simulations were performed in Abaqus 2018, with the use of an in-house crystal plasticity code to describe a user defined material response. In order to figure out the size of Representative Volume Element for FEM simulations, a preprocessing step was accomplished. In this step, starting from the lowest number of hexagonal grains, the grain numbers were increased and this procedure was repeated for three times with generating three sets of random grain orientations. It was simply observed that for a specific grain numbers, macroscopic hardening was reproduced for all three sets within a short bound of tolerance. In the main step, the macroscopic flow curves achieved for single phases were supplied as an input for various mean field schemes. In parallel, finite element simulations of an RVE with two phases were implemented using crystal plasticity material model. This procedure is aimed at evaluating mean field method in comparison with crystal plasticity estimations of material response, regardless of grain size. As a result, a comparison was made between these two methods for two phase materials composed of various volume fractions of inclusion and matrix.

2 Crystal plasticity Simulations

In this section, finite element simulations in Abaqus are performed for RVEs made of hexagonal grains subjected to tensile loading under plane strain conditions. The use of hexagonal grains is beneficial since it makes it possible to increase the number of grains with a constant grain size and to find the minimum number of grains in the RVE which is representative of macroscopic material behavior. In all of these simulations, in-house rate-independent crystal plasticity code was applied as a user defined material model.

In the crystal plasticity model, plastic deformation is assumed to occur due to crystallographic slip that happens on slip systems and other deformation mechanisms such as twinning or transformation induced plasticity effects are not taken into account. In this formulation, total deformation gradient for finite deformation is multiplicatively decomposed in the form [11]:

In which Fᵢ designates the inelastic deformation caused by glide of dislocations and F̂ₑ stands for elastic stretching and lattice rotation happening for a deformed material point at an intermediate configuration. The total velocity gradient L is calculated as [11]:

The inelastic part of the total velocity gradient tensor is computed as the summation of shear rates γ̇^(α) of the slip systems (slip direction s^(α) and slip plane normal m^(α) ) as [11]:

As a flow rule in this formulation, slip occurs once the resolved shear stress τ^(α) of the slip system SYMB is equal to its slip resistance τ_f^(α). Hence, one can define φ^(α) for each slip system as:

The resolved shear stress is obtained by projection of Cauchy stress tensor over slip systems. The details regarding calculation of resolved shear stress is found in [11]. It is worth noting that the principle mechanism for work hardening is considered to happen by impediment of dislocations motion by increase of the forest dislocation density. Hence a Taylor type hardening law is utilized as:

Where 𝜏₀ is the lattice friction, 𝜇 is the shear modulus, b is the Burgers vector length, ρ^(𝛽) is the total dislocation density of the slip 𝛽 and Q^(α𝛽) is the interaction matrix between the slip systems.

In finite element simulations, first of all, a preprocessing analysis is performed for the single phases separately, including FCC and BCC properties attributed grains. The properties are chosen in a way that phase contrast is capable of assessing mean field results more critically. It is worth mentioning that although grain orientations are assigned randomly, it is checked if the disorientations data, computed between any two adjacent grains, follow Mackenzie [12] distribution function for probability densities of disorientation angles. Hence, it ensures that texture is avoided while generation of grains orientations. For the sake of clarity, distorientation angle is defined as the smallest value of all symmetrically equivalent misorientations. Afterwards, macroscopic hardenings belonging to each constituent phase is obtained. In the final step of this section, crystal plasticity simulations of the compound material consisting two phases is performed to extract macroscopic flow curves of the mixture.

2.1 Single phase simulation

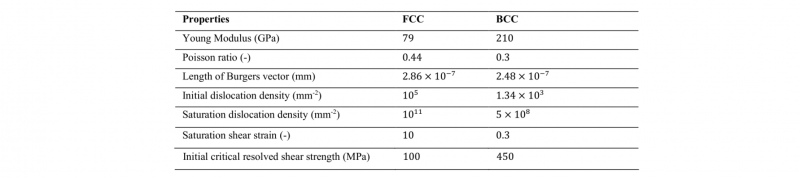
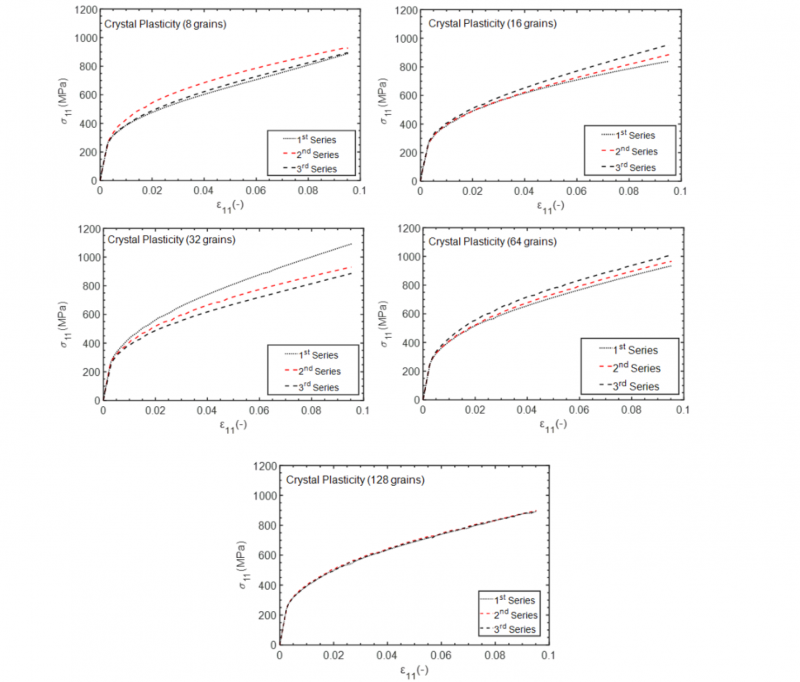
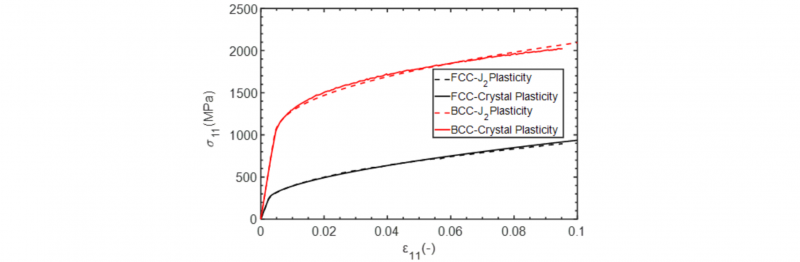
Representative Volume Element used in FEM simulations is displayed in Fig. 1. Periodic boundary conditions are applied on the RVE. Material properties for FCC and BCC grains are listed in Table. 1. In order to find the size of the RVE that can represent macroscopic material behavior, the number of grains were chosen as 8, 16, 32, 64 and 128. Random grain orientations are generated three times for each of the mentioned grain numbers. Once for each number of grains, macroscopic hardenings obtained for three sets of orientations converge to a single curve, that specific number of grains can represent the material behavior in macroscopic scale. As an example, the procedure to find the RVE size for FCC attributed grains has been depicted in Fig. 2. It is clearly seen that for 128 grains, flow curves have converged to a specific trend within a small tolerance. Thereby, it can be deduced that an RVE made of 128 grains is small enough to distinguish microstructural effects and large sufficiently to represent macroscopic material behavior. With 128 grains, 7860 triangular elements (6-node quadratic plane strain CPE6H) were employed in finite element simulations.

Fig. 1. RVE made of 32 grains under prescribed loading.

Table 1. FCC and BCC properties.

Fig. 2. RVE size determination for FCC attributed grains.

In the next step, for the macroscopic hardening found for 128-grain RVEs composed of FCC and BCC grains, a curve fitting of power law (Ludwick) is performed. Power type hardening used for fitting is expressed in Eq. 6 and material parameters achieved from curve fitting are presented in Table. 2.

Fig. 3. Fitting macroscopic hardening.

Table 2. Phase parameters for Ludwick’s equation.

2.2 Two phase material simulation

A two phase material composed of FCC and BCC grains is considered as the mixture. In this stage, a finite element simulation was performed on the mixture of two phases using crystal plasticity code as the material model. The loading conditions are identical to previous section. A parent phase is assumed firstly with second phase assigned randomly as disperse grains among first ones. Three states of volume fractions were considered: State A) 70 % FCC and 30% BCC, State B) 50 % FCC and 50 % BCC, State C) 20 % FCC and 80 % BCC.

In the compounds made of two or more phases, unequal strain and stress partitioning occurs as a result of the contrast among constituent phases. Mean field method is one of the most computationally efficient homogenization techniques that is based on the average values of the field variables in subdomains. There are various schemes in this method that differ principally in the definition of far field strain. Most of them make use of Eshelby’s equivalent inclusion theory which relies on the analytical solution available for a single inclusion embedded in an infinitely long matrix [13]. In these schemes, strain or stress that is concentrated in each phase is related to the total average strain or stress using a concentration tensor. In this paper, four various schemes namely Voigt, Reuss, Bound-Interpolation and Self-Consistent are focused. In Voigt (iso-strain) scheme, strain concentration tensor is equal to unity whilst in Reuss (iso-stress), stress concentration is unit tensor. In Bound-Interpolation method, a simple interpolative approximation between Voigt and Reuss is applied. In the last scheme, called Self-Consistent, the average strain on the RVE is considered to be the far field strain. Consequently, the inclusion is assumed to be embedded in a matrix with the homogenized RVE elastic properties. The derivation of strain concentration tensor as well as the underlying assumptions for the aforementioned schemes are elaborated in [14].

In this section, with the use of microscopic hardenings obtained for constituent phases in section 2.1 as input, various mean field schemes are employed to evaluate the two phase material response.

4 Results and Discussion

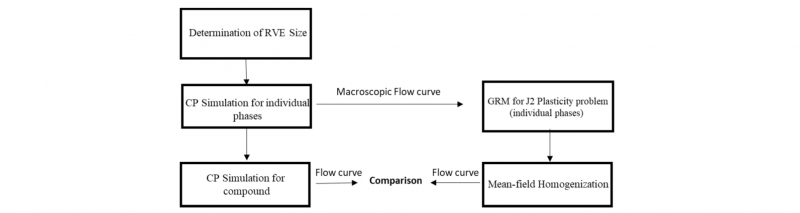
In this section, initially a flowchart (Fig. 4) is drawn to display the numerical procedure that has been taken in this paper and afterwards the results are presented. Macroscopic response of a two phase material, as well as individual phase behaviors, obtained from crystal plasticity simulations and mean field method (Self-Consistent scheme), have been compared in Figs. 5-7. It should be pointed out that the results of section 2.1. for single phases have been employed as input to mean field model. The compound material is composed of FCC and BCC grains and the comparison in Figs. 5-7 is made for various volume fractions of the phases.

Fig. 4. Representative flow-chart of the numerical procedure.

It can be observed in Fig. 5 that Self-Consistent estimations of 𝜎₁₁ stress component versus 𝜀₁₁ for various volume fractions are in a good agreement with crystal plasticity outcomes. It is clearly displayed in Fig. 5 that with increasing volume fraction of BCC from 30 % to 80 %, the compound material behavior is approaching BCC curve. Therefore, it can be inferred that increasing BCC phase volume fraction, has increased the strength of the compound (Two phase material) significantly as it is anticipated. Based on Figs. 5-7, for both crystal plasticity and Self-Consistent results, the end points of individual phases (FCC and BCC) curves as well as two phase material curve are located on a linear line with a specific slope. It implies that the compound material behavior follows the partitioning condition as

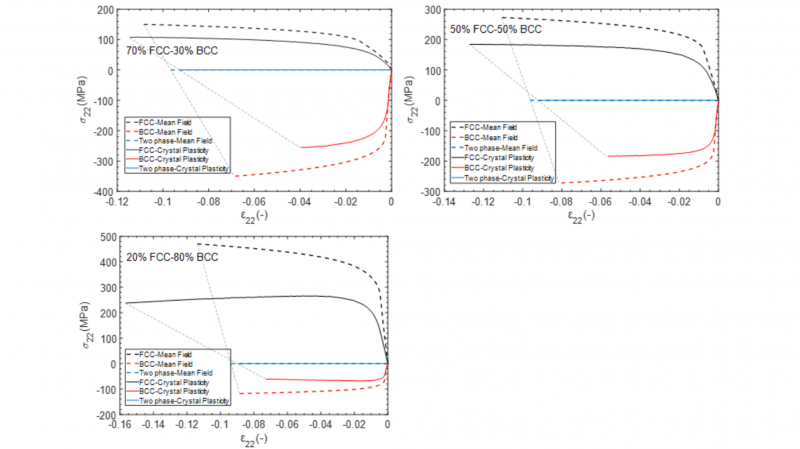
In Eq. 7, f_FCC and f_BCC denote FCC and BCC volume fractions and (ij=11,22,33) indicate various strain and stress components. The loading conditions on the RVE displayed in Fig. 1 besides plane strain elements in finite element simulations, imposes the existence of two stress components (σ₁₁ and σ₃₃ ). Although σ₂₂ has been displayed in Fig. 6, its average value over the two phases equals to zero.

Fig. 5. Schematic illustration of stress and strain partitioning (σ₁₁ versus ε₁₁).

The deviation between Self-Consistent and crystal plasticity method results is pronounced in Figs. 6 and 7 since the stress and strain partitioning among phases is highly dependent on the choice of yield surface. The other point to be focused is that in mean field part, J₂ plasticity formulation and consequently Von-Mises yield criterion is used. In this paper, a hardening curve fitting for single phases was performed for σ₁₁-ε₁₁ components as displayed in Fig. 3. Hence, the agreement between σ₁₁-ε₁₁ outcomes depicted in Fig. 5 proves that once a proper yield surface is fitted based on crystal plasticity illustrations, Self-Consistent scheme is capable of predicting stress and strain partitioning trends accurately.

Fig. 6. Schematic illustration of stress and strain partitioning (σ₂₂ versus ε₂₂).

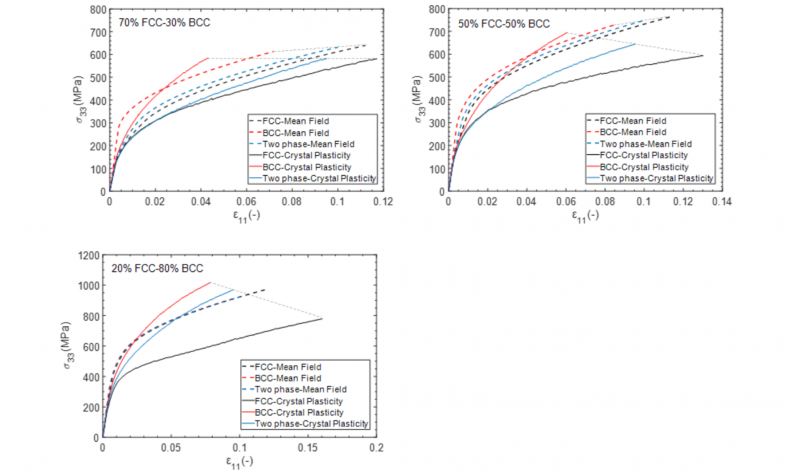
Due to plain strain conditions employed in finite element simulations, ε₃₃ is zero. Therefore, σ₃₃-ε₁₁ is illustrated in Fig. 7. Additionally, four various mean field schemes, including Voigt, Reuss, Bound-Interpolation and Self-Consistent, have been implemented with the use of material inputs obtained in section 2.1 and the outcomes are illustrated in Fig. 6.

Fig. 7. Schematic illustration of stress and strain partitioning (σ₃₃ versus ε₁₁).

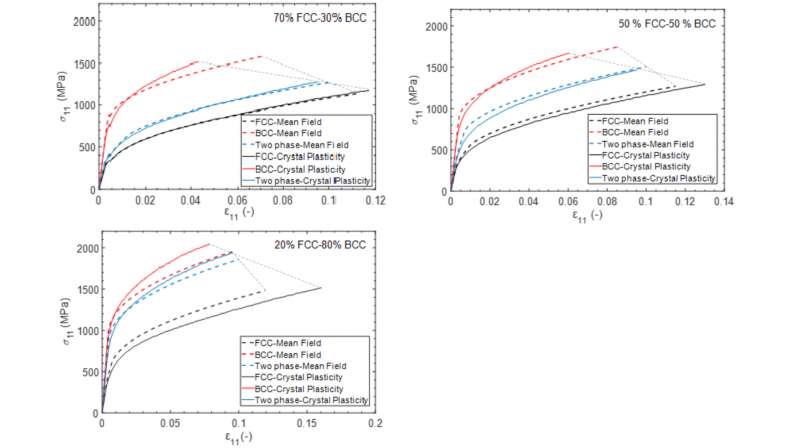
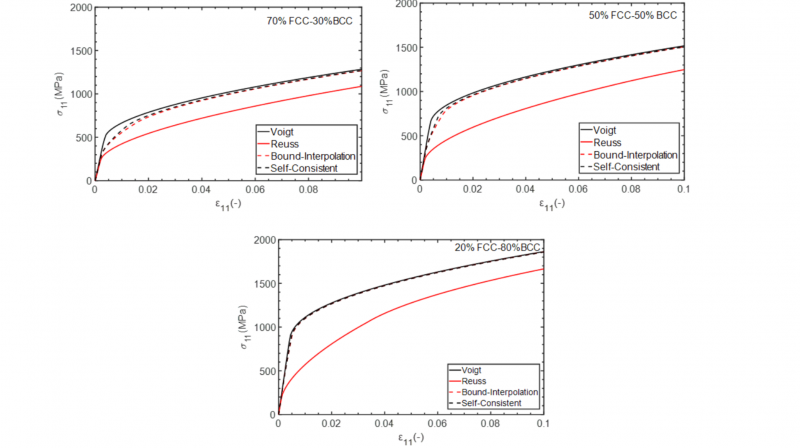
According upon Fig. 8, for the specific material used in this paper, Reuss scheme is not capable of predicting accurate results due to infeasible presumptions and its estimations are deviating critically compared to the rest of schemes and the difference gets more noticeable in States B (50 % FCC-50 % BCC) and C (20 % FCC-80 % BCC). Voigt and Bound-Interpolation schemes give accurate approximations compared to Self-Consistent for this material. However, their accuracy cannot be generalized to all types of material properties because of the underlying assumptions of these two schemes. Voigt scheme overestimates yield strength for States A and B bit not in State C. In the last state, the compound is approaching a single phase material and consequently the assumption of iso-strain is somehow feasible.

Fig. 8. Macroscopic hardening of two phase material obtained from various mean field schemes.

5 Concluding Remarks

In this paper, a comparison was made between two well-known multiscale methods, crystal plasticity and mean field. Firstly, the macroscopic mechanical behavior of single phases was investigated individually by means of finite element simulations where a rate-independent crystal plasticity subroutine was employed as material model. The obtained hardening behavior for constituent phases were titled in the form of power law hardening to be supplied to mean field model. In the latest step, macroscopic material response for the compound, obtained by crystal plasticity simulations and mean field method, is compared. The results indicate that :

• Stress-strain partitioning illustrations obtained from both Self-Consistent and crystal plasticity methods shows that the end points of phase flow curves besides compound material are placed on a linear line with various slopes due to different assumptions used in these methods.

• Self-Consistent scheme can estimate stress and strain partitioning among constituent phases compared to crystal plasticity results once it is provided with an appropriate yield surface.

• Bound-Interpolation and Voigt schemes may assess hardening behavior of the material accurately depending on the choice of material properties.

Acknowledgements

This research was carried out under project number T17019a in the framework of the Research Program of the Materials innovation institute (M2i) (www.m2i.nl) supported by the Dutch government and TATA Steel company.