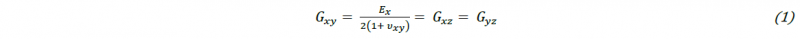1 Introduction

Anisogrid composite lattice structures (ACLSs) are composed of dense system of unidirectional composite helical, circumferential and axial ribs made by continuous filament winding. They are used mainly in the form of cylindrical or conical shells. Lattice inter-stages, payload attach fittings and spacecraft structures have been developed in several space programs [1].

Many researches have been done in the last years, focusing on static and dynamic performances under several mechanical loads. Axial compression loads can cause local or global structural instabilities [2]. Many contributions discussed these aspects, focusing on their numerical prediction via finite element method (FEM). Morozov et al. [3] investigated the buckling behavior of cylindrical ACLSs under axial compression, transverse bending, pure bending, and torsion. In [4] the authors predicted the axial deformability of filament-wound composite anisogrid lattice tubular body of the spacecraft subjected to compressive loading. Moreover, concerning numerical approaches, geometrical optimization procedure has been investigated in [5] for cylindrical ACLS under multiple external loads. An experimental verification of the local buckling failure of ACLSs has been proposed by Totaro et al. [6]. Experimental tests on anisogrid specimen cells have been also proposed in [7], where a multi-failure theory is proposed, including global buckling, local in-plane buckling, local out-of-plane buckling, Euler buckling and material failure.

Concerning the manufacturing processes, filament winding of thermosettings (TSs) and autoclave molding [8] are the most consolidated processes. In fact, despite multiple contributions in ACLSs modeling and structural prediction, researches on innovative manufacturing processes and materials are rare. A valuable contribution is discussed in [9], where authors proposed a new manufacturing process based on robotic dry-filament winding with TS resin infusion and out-of-autoclave curing.

Thermoplastic (TP) matrix composites are becoming more and more interesting for their great potential in aerospace field. TP composites possess outstanding properties in terms of productivity, prepreg storage, easiness of molding, and repairing. Moreover, autoclave is not needed requiring only a simultaneous application of pressure and heat thus simplifying the manufacturing facilities. TP composites generally exhibit greater toughness and higher resistance to impulsive loads resulting very promising for ACLSs application. The idea to introduce TP composites for ACLSs was treated in [10], where the authors developed a full technological assessment about manufacturing of TP ACLSs. In order to keep the manufacturing costs low, polypropylene (PP) TP matrix with glass fibers (GFs) prepregs was preferred. The technology was based on the combination of cold prepreg deposition and out-of-autoclave (OOA) consolidation, avoiding the traditional autoclave step. TP prepreg tapes are winded at room temperature in the final lattice configuration. TP ACLS with un-consolidated filaments is then inserted in an expanded heat-shrink tubing and all components were exposed to heat in a muffle. After the exposition to the heat flux, the tube shrinks applying a uniform pressure on the un-consolidated deposited prepreg. Finite element modelling and mechanical tests were performed to predict mechanical performances of TP ACLSs.

The present work aims at presenting the results of buckling tests performed on cylindrical ACLSs, extending the results showed in [10]. In this case, cylindrical ACLS has been tested under axial compressive load to failure. A parametric finite element model (FEM) of the lattice structure under compressive load has been developed. Numerical modelling was used to correlate the buckling response of the ACLS with composite material properties obtained by OOA process and geometrical features. A comparison between numerical and experimental results has been done, establishing the model predictability. Density measurements were performed on the ACLS to evaluate the soundness of the manufacturing process in terms of layers compaction and void grade; the cylindrical ACLS density was therefore compared with the nominal prepreg density.

2 Materials and Methods

2.1 Materials

Unidirectional (UD) E-GF/PP prepregs (by Jonam Composites Ltd, UK) were used to produce cylindrical ACLS. The initial thickness of the tape was 0.40±0.01 mm whereas the bulk and the area density were 1.40±0.01 g/cm³ and 590 g/m², respectively. There was a difference between these density values and nominal data from manufacturer’s datasheet. A burning test (at 600°C in air) was performed to evaluate the real glass content attested at 51.3±0.1 wt%. Assuming the E-glass density equal to 2.55 g/cm³ (by Azo Materials Datasheet) and the PP density to 0.946 g/cm³ (fully crystalline), the resulting volumetric glass content was 29.4±0.1 vol%, in absence of voids. Being this value lower than the nominal fiber volume content, it is responsible for the difference between nominal and measured density. The prototyping nature of the used prepreg could be responsible of the material non-homogeneities. In fact, some cavities and fiber undulations are often visible on the tape. By considering that the theoretical density of a GF/PP composite with a filler content of 51.3 wt% is 1.42 g/cm³, a porosity of 1.4 vol% is inferred.

2.2 Cylindrical ACLS winding and consolidation

A tape with 2 mm of width was cut from the TP prepreg roll and used as filament to produce TP ACLSs. In this case, an aluminum cylindrical mold has been designed to simplify composite winding and sample extraction. The extremal grooves (12 for each extremities) were used as constraints for the deposition of the helical ribs without breaking the tape continuity. By varying the number of grooves for the tape crossing, it is also possible to produce different geometries of the ACLS with the same mold. In this case, only one geometry was manufactured, with 15 prepreg layers and one helical angle (ϕ). Geometrical parameters are reported in Table 1.

Tab. 1. Geometrical details of mold and ACLS manufacturing operations.

The tape has been wounded manually at room temperature, guaranteeing the correct pull to ensure the prepreg grip on the mold and the adhesion between adjacent layers. A hot soldering iron has been used to weld some points along the deposition path avoiding the mutual sliding between layers. The filament has been wounded alternating one extremity to the other of the cylinder obtaining the helical paths. Each helical and circumferential rib has been obtained continuously without cutting the prepreg tape. This solution allowed reducing weak points due to the manufacturing operations.

The full manufacturing procedure for the cylindrical TP ACLS is shown in Figure 1. After tape deposition, the un-consolidated ACLS is inserted in the heat-shrink tube. Then, the composite is put in the oven for the consolidation. As final step, the full assembly is cooled in water and the part is extracted by removing the heat-shrink tube.

As previously mentioned, thanks to heating provided by a muffle furnace, the heat-shrink tubing reduces its diameter, and starts to compress the TP layers on the mold. This ensure the compression of multiple TP prepreg layers needed for consolidation. Cylindrical ACLS was manufactured by using heat-shrink tubes with proper initial and final diameter to correctly fit with the external diameter of the un-consolidated composite. In particular, the 105/35 heat-shrink tubing was used on the 80 mm cylindrical mold. A uniform consolidation pressure of 10 kPa can be approximately considered for all the sample length according to experimental data on heat-shrink tubes discussed in [10]. TP composites were consolidated for 1 h at 200°C in an oven.

Fig. 1. Manufacturing steps of the proposed OOA process for cylindrical ACLSs production.

2.3 Numerical Modelling

FE model of TP ACLS under axial compressive load has been developed to correlate the buckling behavior to the material properties determined by the proposed manufacturing process and its geometrical features. Thanks to a parametric batch procedure, complex shape of ACLS have been implemented in FEM modelling a fiber orientation and layers superimposition.

Figure 2a shows the parametric modelling for the TP ACLS geometry. The structure is obtained by repeating an ACLS unit in linear and circular arrays. The geometry of this unit is defined by 5 parameters: the helical angle , the width (wd) and the thickness (th) of helical and circumferential ribs, and the distance between two circumferential ribs (d). The final anisogrid structure is meshed with SOLID45 elements.

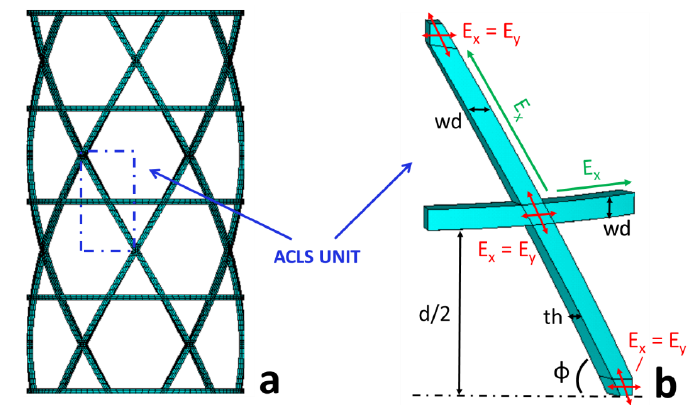Fig. 2. Finite element model of TP ACLS. (a) Complete model, (b) un-meshed ACLS unit.

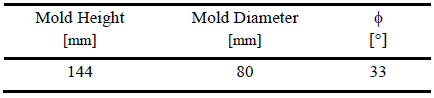
Because of the UD tape, a transverse isotropic elastic behavior results in all the points of the composite samples apart from the intersection points of the ACLS. In the FE simulation, an orthotropic elastic material model has been used for the composite: Young’s modulus along beam direction, E_x, and transverse direction, E_y were extracted from the calibration procedure. According to the transverse isotropy of the composite ribs and panels, the third tensile Young’s modulus E_z was been considered equal to E_y. The Poisson’s coefficient is 0.22 for the E-glass and 0.42 for PP. By applying the mixture law and considering the transverse isotropy as well, the Poisson’s coefficients υ_xy, υ_xz, and υ_yz have been set equal to 0.36, 0.36, and 0.33, respectively. In addition, the following expression has been used for the shear moduli:

which is largely used in first approximation for numerical simulation of composite materials. These assumptions on Poisson’s coefficients and shear moduli are strong, but they are not expected to play a key role in the used compression configuration. In the case of the ACLS, the compression behavior of the individual ligaments should dominate the elastic response of the structures except for small regions close to the constraints. Material Young’s moduli have been extracted experimentally and inserted in FE model according to calibration and validation procedure widely discussed in [10].

The single anisogrid unit has been modelled and subsequently imported in FEM environment The basic element is composed by 7 volumes (see Figure 2b). In the ACLS, fibers are oriented along these volumes but the winding manufacturing process determines intersection zones where the number of layers doubled than in the ribs; in addition, the material behavior is orthotropic due the intersection of circumferential and helical ribs. In order to compensate this mismatch an approximation was introduced: the same elastic modulus was used in the longitudinal ribs, but it was applied both to E_x and E_y. The increase in thickness was not considered geometrically but using for the transverse elastic modulus the double of E_z of the ribs. The final model consisted of 20736 elements.

2.4 Density measurements and buckling testing

Several density measurements have been performed on the ACLS, thus evaluating the prepreg compaction. Specifically, a hydrostatic balance was used for density measurements. A universal material testing machine (MTS Insight 5) was used for this purpose, with a sensitive load cell with maximum load of 100 N. The ACLS was measured several times suspending the ACLS in contact with load cell, before the immersion in water; then the same measurements have been performed dipping the ACLS in water. Elaborating the results, it was possible to extract the density values of the complex shaped ACLS.

ACLS sample was tested in axial compression configuration by the universal material testing machine (MTS Alliance RT50) with a test speed of 1 mm/min up to failure. A pre-load of 50 N was applied to reduce initial non-linearities due to the non uniform contact with the compression plates. Figure 3 shows the ACLS under testing just before and after the collapse.

Fig. 3. Axial buckling test on ACLS. (a) ACLS just before and (b) after collapse.

2.5 Results and Discussion

Density measurements have proved the correct shaping and agglomeration of the TP composite structures. Density data for cylindrical ACLS has been 1.38±0.02 g/cm3, very close to the theoretical prepreg density (1.42±0.01 g/cm3) determining a small void content (~3%) despite of the absence of vacuum during molding. Accordingly, the OOA fabrication method allows good consolidation despite of the low applied pressure. The proposed technology seems to reduce the negative influence of the low fluidity of the molten polymer matrix. Generally, by using heat-shrink tubes to apply pressure during molding, high densities are reached with small distortions and layer interpenetrations.

Figure 4a reports the force-displacement curve, extracted by the buckling test. The curve starts without any non-linear branch thanks to the preload applied of 50 N. Thanks to the applied pre-load, the initial non-linearity due to non-perfect contact between compression plates and sample was avoided. The linear branch is clearly defined, and it is characterized by a slight loose of load approximately at 0.8 mm. This is probably due to local damages started in correspondence of the upper part of the structure. The limit point has been reached at about 1.5 mm of displacement, with force peak of 4874.8 N. At this point the ACLS exhibit a substantial collapse in the upper part, close to the upper compression plate. This determined a reduction of ACLS ability to bear axial load with slight rise of stiffness at 2.4 mm. This effect is attributable to the remaining part of the structure which briefly supported the upper collapsed one. Increasing the crosshead displacement, a significative drop of force has been registered up to 15 mm, while a plateau has been reached approximately in the range from 15 to 40 mm.

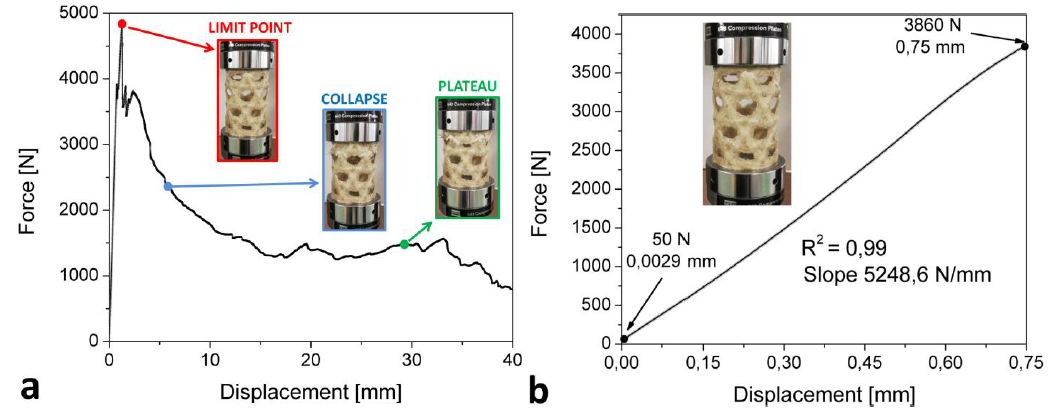Fig. 4. Force-displacement curves of ACLS under axial buckling loading. (a) Entire curve with buckling phases and (b) detail of the first elastic region for stiffness value extraction.

Analyzing the elastic region before the beginning of instability, it has been possible to extract the stiffness of the structure as slope of the interpolating force-displacement curve. Figure 4b shows the elastic region, that ends approximately at 0.75 mm with maximum load of 3860 N. The approximation to linear curve is very close and a stiffness of 5248.6 N/mm has been evaluated.

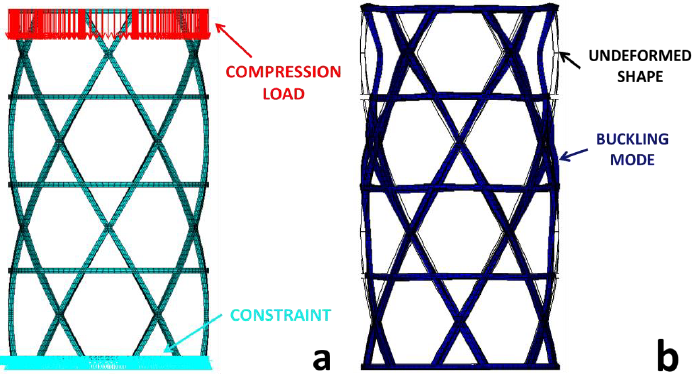Fig. 5. Finite element model of ACLS under axial compression load. (a) Model with loads and constraints, (b) buckling mode and undeformed shape.

The maximum instability load has been also extracted numerically performing a buckling analysis. An axial compressive load of 1 N has been applied on the upper nodes reproducing the compression determined by testing machine. On the other hand, all lower nodes have been constrained (Figure 5a). Figure 5b shows the buckling failure mode corresponding to eigenvalue (λ) of 6.149. The failure mode is characterized by a substantial collapse of the helical ribs in the upper part. According to instability theory and the numerical modelization approach, the failure load corresponding to the eigenvalue λ shall be determined by multiplying the number of loaded nodes by λ, being unitary the compressive load. The numerical load was 5288.1 N and determined an error of 8.5% compared to the experimental value. As result, the proposed numerical modelling approach is quite close to the experimental observations. From manufacturing point of view, the good agreement between numerical and experimental results is a way to assess the quality of the proposed OOA manufacturing process for TP ACLSs. Numerical results suggest that a good compaction was obtained between TP prepreg layers during molding, as the mechanical behavior of the ACLS does not differ significantly from the theoretical one. The produced TP ACLS achieved expected performances, despite of the use of manual operations and commercial heat-shrink tubes, typically not used for composite manufacturing. This evidence could be related to the robustness of the experimental methodology and the parametric numerical approach. All the stages of the manufacturing process were made by considering the need of a process scale-up toward industrial scenarios.

2.6 Conclusion

The proposed OOA manufacturing method uses heat-shrink tubing for compaction the UD TP prepreg layers. This technology can be suitable to produce multiple TP ACLSs by using big ovens where vacuum or pressure is not necessary. This can reduce the facilities investment costs and complexity. A limitation impacting the final aesthetic result of the ACLS is the appearance of the resin squeezing out phenomenon during the consolidation phase. On the other hand, this effect does not affect the mechanical response of the structure. Over-molding operations could be taken into consideration to overcome this aesthetic yield.

Concerning the results presented in this work, axial compression tests have been performed extracting the maximum load at instability phenomena. The ACLS by OOA process exhibit great mechanical performance reaching high loads before undergoes buckling and collapse. This is very promising considering the multiple manual operations that determined multiple geometrical imperfections on the structure. Furthermore, the results seem to be very attractive considering the prototype nature of the used TP prepreg PP/E-glass fibers. FE model has been constructed in order to predict numerically the mechanical behavior of the TP ACLS under axial loads. Numerical results match with the experimentation, providing a good ability to predict the buckling modes of ACLS. Due to the parametric nature of the numerical model and the calibration phase described in [10], it is very simple to evaluate the mechanical behavior of ACLS changing several geometrical parameters under the axial compressive loads.

As general consideration, cylindrical ACLSs are used for aerospace but the proposed OOA process could also open new industrial uses for this family of composite structures. In fact, TP composites have great potential in terms of mechanical performances in static conditions as well as in dynamics, providing high toughness and impact resistance. For these reasons, TP composite seems very optimal candidates to produce ACLSs typically subjected to high-impulsive aerospace loads.

Acknowledgements

Authors are grateful to Dr. Fabrizio Betti for the support in the experimentation.