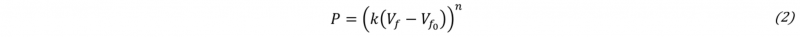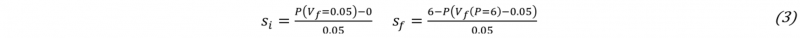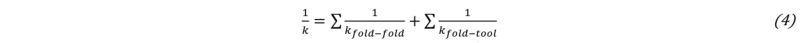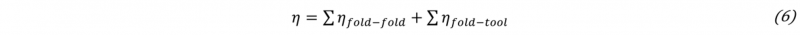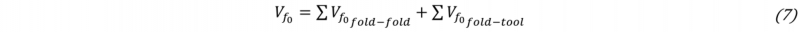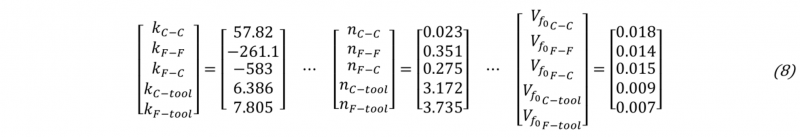1 Introduction

With the new legislations for more environmentally friendly materials, composite reinforcements made from plant fibres, especially flax fibre, have been developing significantly. The hybridization of these reinforcements with some conventional synthetic fibres is also a current trend [1-7]. Most studies focus on the properties of hybrid laminate composites after consolidation. However, the compaction of fabric stack before or during their impregnation with a polymer matrix is a crucial key-point of the control of the manufacturing process and of the future technical properties of the consolidated composite [8]. In resin transfer molding process, the knowledge of compaction behavior is necessary to predict the resistant forces during the closure of the mold. In infusion process, even if the applied pressure is limited to atmospheric pressure, the fabric stack deformation the must be known to optimize the resin flow during impregnation. In this study, various stack sequences made of carbon and flax fibre reinforcements have been tested experimentally in compression. In a first step the compaction curves obtained for various hybrid stack sequences are compared and fitted with a modified Van Wyk model. In the second section, to compare more precisely the compaction curves, we proposed to cut them in three specific phases, corresponding to three mechanical states of the stacked fabrics. The last section is devoted to a proposition of decomposition method of the parameters of the compaction model as a function of the stack sequence.

2 Materials

The flax fabric chosen for this study, commercialized under the brand name Twinflax, is a complex plain weave (Table 1) where a tow is made of five twisted yarns and the yarns of warp and weft tows are interlaced (Fig. 1). The yarn diameter is equal 0.374 mm, ±30%. Taking into account the spacing between warp tows (0.866 mm ± 16%) and weft tows (0.773 mm ± 14%), the flax fabric is relatively low filled. The carbon reinforcement is a common 2/2 twill made of continuous fibres, assembled in flattened tows, and is completely filled with no gap or lack of material observable on a backlight photo (Fig. 1). Coming from the textile industry, the chosen flax fabric has not been designed for composite manufacturing. An additional objective of the hybridization with carbon reinforcement can be to overcome the weak manufacturing characteristics of flax textile fabrics, with some nesting effects of the deformable carbon fabric in the low-filled flax fabric [9].

Table 1. Flax and carbon fabric characteristics.

Fig. 1. Patterns of flax and carbon fabrics. (a) TexGen 3D modelling of flax fabric, (b) backlight photo of flax fabric and (c) backlight photo of carbon fabric.

3 Experimental procedure

The compaction test consists in applying perpendicular pressure to the plane of the reinforcement fabric stack. The purpose of this test is to quantify the change in thickness of the fabric stack as a function of the applied force. Fabrics are carefully cut into discs of 120 mm diameter. All layers of a stack are oriented in the same direction, with the same surface facing up. Compaction tests are performed on a mechanical testing machine, equipped with a 5 kN force sensor and piloted at a displacement speed of 0.5 mm/min. The gap between the mobile compression plate and the fixed one is measured with a LVDT sensor. The diameter of compression plates is 100 mm, their flatness and relative parallelism have been carefully checked. Each test has been repeated more than 5 times.

4 Compaction model

4.1 Compaction model presentation

In this modified version of the Van Wyk model [10], the applied compressive pressure P is related to the fibre volume ratio V_f in the preform stack with three parameters: the stack sequence stiffness k , the fibre volume ratio at zero pressure V_f0 , and the sensibility to pressure n (2). As it will be shown in a second part of the paper, the stiffness k of a hybrid sequence can be defined by the sum of elementary stiffness. It seems then more consistent that the total stiffness of a stack sequence is also sensitive to the pressure via the exponent n.

4.2 Identification of compaction model parameters

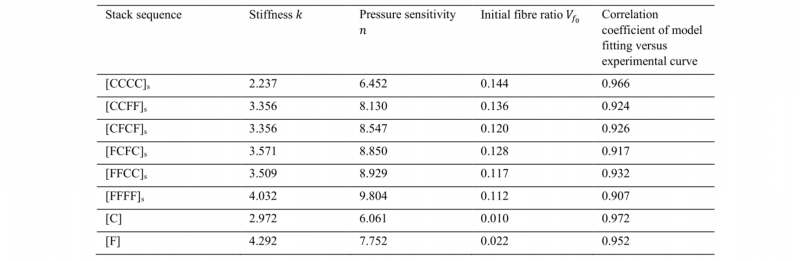
The model parameter identification is performed with a genetic algorithm implemented in Scilab software [19]. The correlation coefficients between the fitted curve and the experimental data prove that this model is efficient to accurately reproduce the experimental results (Table 2).

Table 2. Identified parameters of compaction model.

The behaviour of carbon fabric stack is nearly the same regardless the number of layers. The only difference is the value of initial fibre ratio with V_f0[C] = 0.010 and V_f0[CCCC]s = 0.145. It is the same for flax fabric stack, with V_f0[F] = 0.022 and V_f0[FFFF]s = 0.111. It is obvious that, with a fabric architecture of carbon fabric designed for composite manufacturing, the carbon preform is more compactable that the flax one. Due to the high level of interlacing between the individual yarns of warp and weft tows, the flax fabric is not deformable and compactable. Consequently, compaction stiffness k_[F] and pressure sensitivity n_[F] of the flax fabric are 44 % and 28 % higher than the carbon fabric ones k_[C] and n_[C]. When the number of layer is equal to eight, the same trend are emphasized. k_[FFFF]s and n_[FFFF]s are 86 % and 68 % higher than k_[CCCC]s and n_[CCCC]s.

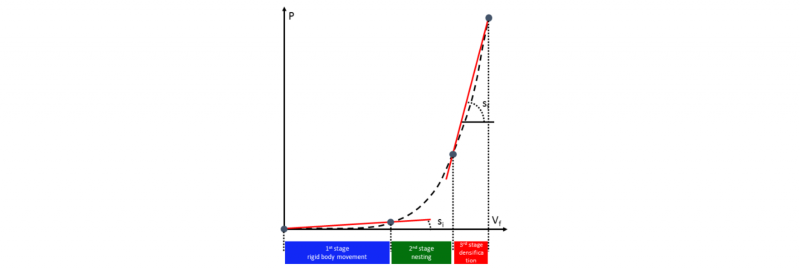
Fig. 2. Definition of the three stages of the compaction curve.

4.3 Identification of the compaction phases

More generally, it is quite difficult to accurately discuss the compaction behaviour from the model parameter values. Indeed, the power law form of the compaction model causes that the effects of the model parameters are not independent of each other. As proposed by Matsudaira et al. [20], the compaction curve can be separated into three distinct parts (Fig. 2). As we have limit the pressure during compaction test under 6 bar, pure compressive deformation stage is not completely achieved and the main cause of observed deformation are due to rigid body movement at the different scale of stack fabrics (layers, tows or fibres). The first stage, without significant increase in pressure and large displacement, is related to relative movement between the layers of fabric stack, these movements make it possible to close the spaces between the layers and put them in contact. The deformation is based only on rigid body movement. The second one is linked to nesting effects by deformation of layers and tows, and is characterized by a non-linear behaviour with a progressive increase of the tangential stiffness. The number of contact between neighbouring tows and between fibres inside the tows increase. The last phase is the densification, based on deformations at various scales with the objective of the disappearance of internal porosities. Deformations are caused by movements and deformations of tows and fibres inside the tows: tow flattening, tow unwavering… During this phase, the global strain of the fabric is weekly evolving whereas the pressure increase strongly.

The first and last phases can be considered as linear, whereas the intermediate phase is strongly non-linear. The transition between the first and the second phases, and between the second and the last phases can be detected by the variation of the compaction curve slope. The interval chosen for the slope estimation is equal to 0.05 (3). As explain by the Fig. 2, the interception of the line of slope 𝑠 𝑖 and starting from the initial point (V_f = 0.0, P = 0.0) define the first compaction stage. By the same way, the last compaction stage is defined by the interception of line of slope s_f and passing through the final point of the compaction curve (P = 6.0).

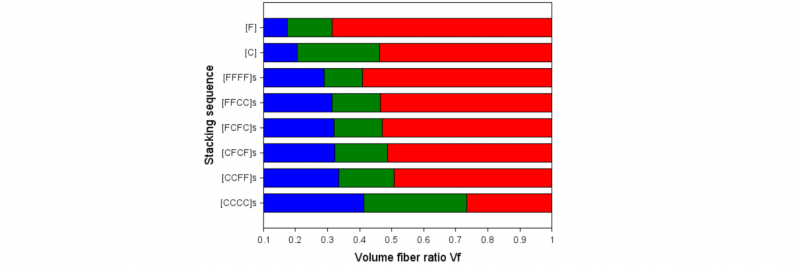
Fig. 3. Evolution of the three compaction stages (rigid body movement in blue, nesting in green, densification in red) as a function of the stack sequence.

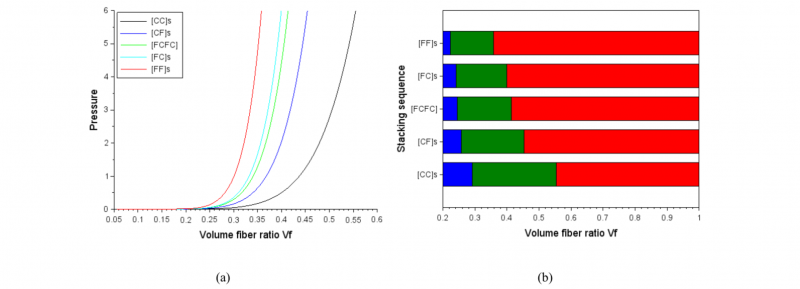
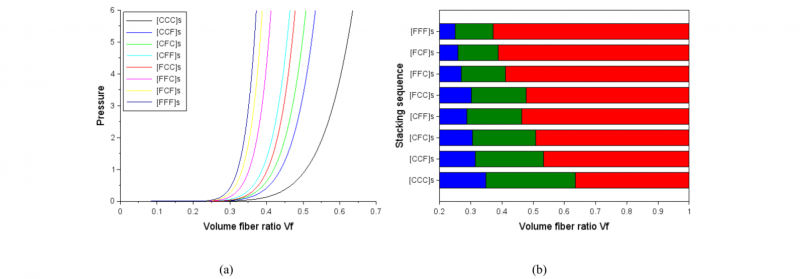
With this method of decomposition of the compaction curve, comparing the behaviour of different stack sequences becomes much easier (Fig. 3). For hybrid stack sequences, it seems that the compaction behaviour of the hybrid sequences is controlled by the outer layers. Indeed the more carbon layers are placed at external positions into the hybrid stack sequence, as for [CCFF]s sequence, the more the compaction behaviour trends to pure carbon [CCCC]s stack sequence behaviour. The same trend is observed with the position of the flax layers. Hybrid stack sequences with flax layers on the external positions, [FFCC]s , are closer to the 100 % flax stack sequence [FFFF]s than [FCFC]s and [CFCF]s. Consequently the compactiblity of the hybrid sequences decreases gradually from [CCFF]s to [FFCC]s. Indeed the [CCFF]s sequence is the more compactable one among all the tested hybrid sequences; and generally the compactiblity depends on the position of the layers of carbon and flax in the stack sequence.

This experimental finding is a little bit surprising as the initial idea was to use the high compactibility of the carbon fabric to compensate the low compactibility of the flax fabric. By alternating flax and carbon layers in [FCFC]s and [CFCF]s stack sequences, the carbon layers had to deform and fill the void of the flax one, and by this way increase the global compactibility of the hybrid staking sequence. This idea is more or less inaccurate; other phenomena seem to be involved in the compactibility of a hybrid sequence. A hypothesis that could explain this fact is that the compression pressure is not evenly distributed throughout the layer stack. External layers are first and more compressed than the internal ones. Consequently the four external C layers of the [CCFF]s sequence are firstly compacted, the global sequence strain is only due to the rigid body movement of the external carbon layers and the applied force remains low. When the gap between the two compaction plates is decreasing, the internal layers are involved into the compaction behaviour. Internal flax layers, not very sensitive to rigid body movement, enter fairly quickly in the compaction phase by nesting, which causes a rapid increase of the pressure. The end of the compaction process is then made of a mix of nesting and densification of flax and carbon layers.

The global behavior of the [CFFC]s stack sequence is the same as for the [CCFF]s sequence except for the initial compaction phase. During this initial phase, only the two outer carbon layers are active during the compaction start, which leads to a faster passage into the nesting phase.

Concerning sequences with outer flax layers [FCFC]s (one flax layer per face) et [FFCC]s (two flax layers per face), the nesting phase comes even faster, the outer flax layers can not be deformed without increasing the pressure.

5 Compaction model parameters as a function of stack sequence

5.1 Decomposition and identification of elementary parameters

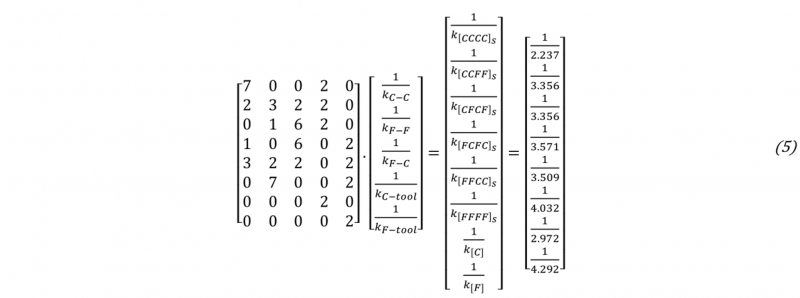
A finer analysis can be done by breaking the global stiffness of a stack sequence k into several elementary stiffness. The global stiffness k is defined by analogy with series-mounted springs (4). k_fold-fold is the stiffness associated to the interaction between two successive layers, and k_fold-tool is the stiffness associated to the interaction between the compressive tool and the external layer of the stack. As the pressure is limited to 6 bars during the compaction test, the mechanisms involved into the deformation of the layer stack are mainly caused by rigid body movements like nesting and tow flattening, while deformations of elementary constituents of fabric layer (fibre and yarn) are still weak. The stack sequence [CLCL]s is described by one interaction between two flax layers k_F-F , six interactions k_C-C and two interactions k_C-tool (5). The same approach can be applied to the other two model parameters, n and V_f0 ,with a parallel-mounted assembly, (6) (7). By solving the three systems, the values of the elementary stiffness, the pressure sensitivities and fibre volume ratios at zero pressure are identified (8).

Starting with the elementary stiffness and using equations (4), (6) and (7) it is then possible to calculate the global stiffness of a stack sequence, and by the same way, the pressure sensitivity and the fibre volume ratio at zero pressure. The confrontation between the model parameter values identified on the experimental curves and the values recalculated is exposed on Fig. 4 and validate the decomposition approach.

Fig. 4. Comparison of the parameters of the modified Van Wyk model identified on experimental compaction curves with them recalculated with the decomposition model.

5.2 Prevision of stack sequence compaction curve

Using the decomposition approach, it is then possible to predict the compaction behaviour of any stack sequence made of carbon and flax layers. The model parameters of a stack sequence are calculated using the stack sequence composition and the value of each elementary parameter. Using this calculated parameters of a stack sequence and the modified Van Wyk model, the compaction behaviour curve of this stack sequence can be predicted.

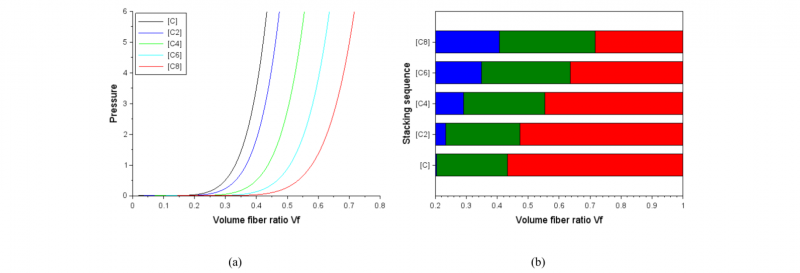
Fig. 5. Compaction of carbon layer stack. (a) simulation of compaction curves of carbon layer stack sequence as a function of the number of layers, (b) evolution of the three compaction stages (rigid body movement in blue, nesting in green, densification in red) as a function of the stack sequence.

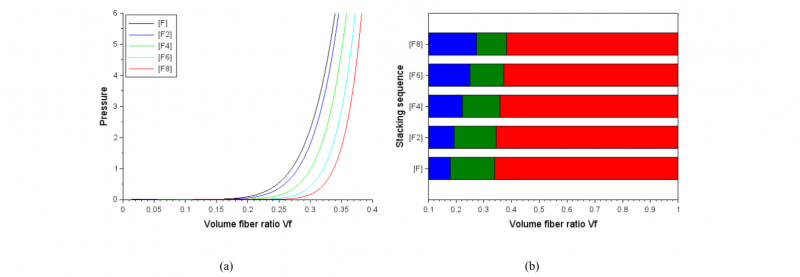
Concerning the stack sequence made with only one type of fabric, the evolution of compaction curve as a function of the number of layers of carbon or flax stack sequences is exposed on Fig. 5-a and 6-a. The flax stack sequences are very little dependent of the number of layers. This is due to the inherent nature of the flax fabric: low deformability and nesting capacities. On the contrary, the stack sequence made with highly deformable carbon fabric are dependent on the number of layers. For each compaction curve, the three elementary phases of compaction (rigid body movement, nesting, and densification) are identified using the same method as previously and plotted on Fig. 5-b and 6-b. The difference of behaviour of each stack sequence becomes obvious and easily observable. We notice a progressive evolution of the behaviour from a stack of one layer to a stack of eight layers. Some aspects are the same for stack sequences made from carbon and those made from flax, others are different. Logically, phase 1, linked to the rigid body movement of the different layers, becomes more and more important when the number of layers increases. This is especially true for carbon fabric stack sequence. For phase 2 linked to nesting between the layers, its extent increases, from 0.228 for a stack of one layer to 0.309 for eight carbon layers; while its extent decreases for flax stack sequence from 0.160 to 0.108. Flax fabric layers are not very deformable and it is difficult for them to fit into each other, and the most important part of the strain is through rigid body movement.

As for stack sequences made of a single type of fabric (carbon or flax), it is possible to predict the compaction behaviour of any hybrid sequence. For example, the compaction curves of hybrid stack sequence made of some four and six carbon and flax layers are exposed on Fig. 7 and 8.

Fig. 6. Compaction of flax layer stack. (a) simulation of compaction curves of flax layer stack sequence as a function of the number of layers, (b) evolution of the three compaction stages (rigid body movement in blue, nesting in green, densification in red) as a function of the stack sequence.

Fig. 7. Compaction of hybrid stack made of 4 flax and/or carbon layers. (a) simulation of compaction curves of 4 layer hybrid stack sequence as a function of the hybridization order, (b) evolution of the three compaction stages (rigid body movement in blue, nesting in green, densification in red) as a function of the stack sequence.

Fig. 8. Compaction of hybrid stack made of 6 flax and/or carbon layers. (a) simulation of compaction curves of 6 layer hybrid stack sequence as a function of the hybridization order, (b) evolution of the three compaction stages (rigid body movement in blue, nesting in green, densification in red) as a function of the stack sequence.

6 Conclusions

The proposed model of the compaction behaviour of stack sequence of dry fabric layers, issued of the Van Wyk model, is based on a set of three parameters (stack sequence stiffness k, fibre volume ratio at zero pressure V_f0 , sensibility to pressure n). The originality of the method is to construct the behaviour law of a complex stack sequence by the assembly of elementary behaviour. Elementary behaviours are identified using a first set of experimental compaction tests and are linked to the interaction of a fabric layer with its surrounding environment (another fabric layer or the surface of the compressive mould). This modelling approach has been tested on various carbon/flax hybrid stack sequences, and seems efficient to model and predict their compaction behaviour. However, the validity of the proposed model is limited to the range of stack sequences of a reduced number of layers. With stack sequences made of numerous fabric layers, some new phenomena must be taken into account and individual behaviour of each layer should be defined as a function of its position in the stack sequence.

In complement we proposed a method to decompose the compaction behaviour curve into three stages: rigid body movements, nesting, densification of the layers. This method is relevant firstly to compare easily some compaction curves and secondly to evaluate the state of internal strain of a stack sequence.