- Accueil
- Volume 17 (2013)
- numéro 2
- Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: a review
Visualisation(s): 0 (0 ULiège)
Téléchargement(s): 0 (0 ULiège)
Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: a review

Notes de la rédaction
Received on November 3, 2011; accepted on December 6, 2012
Résumé
Méthodes de spatialisation de données pluviométriques dédiées à l’hydrologie opérationnelle et à la modélisation hydrologique à l’échelle du bassin versant (synthèse bibliographique). La gestion hydrologique des bassins versants et la modélisation hydrologique exigent des données relatives aux précipitations, variable très importante, le plus souvent mesurée par des pluviomètres ou des stations météorologiques. Les modèles hydrologiques demandent souvent une spatialisation préalable à la modélisation, la spatialisation est dépendante du type de modèle et de son mode de gestion géographique et de la résolution utilisée. La qualité d'un résultat est conditionnée à la qualité de la pluie spatiale continue qui découle de la méthode d'interpolation utilisée. L’objectif de cet article est de fournir une revue sur les méthodes de spatialisation de la pluie existantes qui sont habituellement exigées par la modélisation hydrologique. Nous passons en revue les méthodes de base généralement utilisées et des approches géostatistiques. Les études précédentes mettent en lumière un besoin de nouvelle recherche sur les moyens nécessaires pour améliorer la donnée de pluie et in fine, la qualité de la modélisation hydrologique.
Abstract
Watershed management and hydrological modeling require data related to the very important matter of precipitation, often measured using rain gauges or weather stations. Hydrological models often require a preliminary spatial interpolation as part of the modeling process. The success of spatial interpolation varies according to the type of model chosen, its mode of geographical management and the resolution used. The quality of a result is determined by the quality of the continuous spatial rainfall, which ensues from the interpolation method used. The objective of this article is to review the existing methods for interpolation of rainfall data that are usually required in hydrological modeling. We review the basis for the application of certain common methods and geostatistical approaches used in interpolation of rainfall. Previous studies have highlighted the need for new research to investigate ways of improving the quality of rainfall data and ultimately, the quality of hydrological modeling.
Table des matières
1. Introduction
1Computer hydrological models that simulate most of the hydrological cycle are an essential tool for hydrologists and engineers in understanding and describing the hydrological system. When these models are successful in attaining accurate results, they can forecast what will occur within the hydrological system. This can be useful for climate studies (e.g. in terms of precipitation or evaporation), optimized water management and land use changes: so-called scenario analysis. In the last 30 years, not only the number but also the complexity of hydrological computer models have increased enormously, due to the availability of more powerful computers and Geographic Information Systems (GIS) (Singh, 1995). Watershed models can be categorized as physically-based or conceptual, according to the degree of complexity and physical completeness present in the formulation of the structure (Refsgaard, 1996). In addition, hydrological models are classified as either “lumped” or “distributed”, depending on the degree of discretization when describing the terrain in the basin. The physically-based models describe the natural system using the basic mathematical representations of the flow of mass, momentum and various forms of energy at local scale (Refsgaard, 1996). These models are therefore also described as “distributed” and they can explicitly account for spatial variability within a watershed. Physically-based distributed models are generally believed to be preferable to conceptual models because they better represent a certain reality of the hydrological cycle (Ruelland et al., 2008).
2Fully distributed and physically-based models always require as inputs the main spatially distributed dataset for the Digital Elevation Model (DEM), land use and its management, soil, and climate. The quality of these inputs has a significant impact on the model formulation process and on the results. Climatic data, air temperature, solar radiation, and precipitation all provide essential controls on surface energy balance and ecosystem processes. Among these climatic data, the amount of precipitation, traditionally collected using rain gauges or weather stations, is a very important parameter, which has a direct impact on runoff or watershed discharge (Obled et al., 1994). For a large watershed scale, the spatial variability of rainfall needs to be taken into account instead of using areal average rainfall as the input for the model. In this context, it is necessary to gain insight into the day-to-day spatial variability of watershed discharge, groundwater level and soil moisture content (Schuurmans et al., 2007a). In order to gain insight into the general behavior of the hydrological system, it is sufficient to use accurate predictions of areal average rainfall over the watershed.
3The spatial variability of rainfall represents the dominant effect in the production of runoff; as the spatial variability increases, so does the significance of appropriate rainfall characterization (Segond et al., 2007). Averaging of the rainfall input limits the accuracy of the model’s results. Under such circumstances, catchment response is highly nonlinear, which means that the response to an averaged input will differ much more from the response to a distributed input (Shah et al., 1996b). When a single rain gauge is used to model the catchment response, the results become less accurate at both the sub-catchment and catchment scales and this also affects the reproduction of the hydrograph (Segond et al., 2007). When spatial homogeneity of rainfall is assumed to be used in a hydrological model, rainfall variability causes certain effects to occur. Spatial variability in rainfall affects the catchment response (Shah et al., 1996a; Shah et al., 1996b), the timing of peak runoff (Singh, 1997), the estimation of model parameters (Chaubey et al., 1999) and the hydrological model outputs (Bell et al., 2000; Segond et al., 2007).
4The distributed model has been shown to be sensitive to the locations of the rain gauges within the catchment and hence to the spatial variability of the rainfall over the catchment (Bell et al., 2000). Failing to consider adequately the spatial variability of rainfall will lead to errors in the values of the model parameters, which will be wrongly adjusted to compensate for errors in the rainfall input data (Schuurmans et al., 2007a). This is problematic since the required density of rain gauges to capture the spatial variability exceeds that normally available from routine monitoring networks (Segond et al., 2007). Furthermore, rain gauge density over the forecast catchments is one of the main factors in attaining forecast accuracy during an extreme event that results in significant flooding in a major metropolitan area (Looper et al., 2011). Therefore, the precipitation input, as with other climatic data, should be prepared as spatially distributed data before being forced into the hydrological modeling. However, measuring at every point where data are needed is prohibited by the associated high costs.
5Spatially distributed rainfall can be interpolated by a range of different methods but the complexity lies in choosing the one that best reproduces the most accurate data (Caruso et al., 1998). One approach is to measure associated ancillary data, which have been available since the late 1960s via ground-based meteorological radars and by remote sensing devices located on satellite platforms. The accuracy and consistency of these indirect processes for hydrological purposes still remain to be determined. Techniques for interpolating rainfall must be calibrated and validated by means of historical information (Lanza et al., 2001). From 2000s onwards, standard range-corrected radar products proved to be sufficiently informative to capture the spatial variability of rainfall to be used in hydrological applications (Schuurmans et al., 2007a). In particular, the use of radar products in combination with multivariate geostatistical methods proved to be beneficial for spatial rainfall estimation (Velasco-Forero et al., 2009; Schiemann et al., 2011; Verworn et al., 2011). However for regions without these sophisticated instruments, direct ground-based measurement deserves to be considered for spatial interpolation processes.
6The major problem, prior to the choice of the most suitable interpolation method, is related to the availability of rainfall data. Sometimes, data are continuously recorded but the rain gauges are too scattered. This is particularly true in mountainous areas, where amounts of precipitation are more difficult to forecast due to complex topography, distance to the sea and the presence of large water bodies such as lakes (Johnson et al., 1995; Buytaert et al., 2006). Within a complex topography, the spatial scale features of rainfall are characteristically difficult to capture even by means of a moderately dense network of rain gauges. Topography impacts rainfall pattern through so-called orographic effects, which refer to the rise in precipitation rates induced through altitude due to uplift, adiabatic cooling and resulting condensation of humid air masses on windward mountainsides (Chow et al., 1988). Observation of these orographic effects and weather patterns has prompted ongoing investigation into whether precipitation, in general, increases with altitude (Groisman et al., 1994; Sevruk, 1997; Sinclair et al., 1997). These authors found that the relationship between precipitation and elevation depended on the region’s exposure to wind and synoptic conditions. Depending on the predominant wind direction, rain shadows may appear when more rainfall occurs at or near the mountain peak and much less rainfall occurs at lower altitudes (Sinclair et al., 1997). Even in flatter areas, rain gauges need to be correctly distributed in order to detect air flow influences, thermal inversions and other phenomena that could affect climatic patterns. This difficulty of accurately reproducing continuous spatial rainfall has led to notable failures in the resulting hydrological response models, which are sensitive to input volume at the watershed scale (Nicotina et al., 2008). At a smaller scale, rainfall variability also has a greater impact on peak flows (Mandapaka et al., 2009). As the scale increases, the importance of spatial rainfall decreases and distribution of catchment response time, rather than spatial variability of rainfall, becomes the dominant factor governing runoff generation (Segond et al., 2007).
7The objective of this paper is to provide a review of existing spatial interpolation methods of rainfall, which are required for hydrological modeling. We review the basis for the application of some commonly used spatial interpolation methods and geostatistical approaches and provide an overview of the characteristics of the methods.
2. Spatial interpolation methods for calculating rainfall
8A number of interpolation techniques have been described in the literature, which reproduce the spatial continuity of rainfall fields based on rain gauge measurement. These methods can be generally classified into two main groups: deterministic methods and geostatistical methods. Some commonly used methods are briefly introduced here. Spatial interpolation is generally carried out by estimating a regionalized value at unsampled points based on a weight of observed regionalized values. The general formula for spatial interpolation is as follows:

9where Zg is the interpolated value at the required points, Zsi is the observed value at point i, ns is the total number of observed points and λ = (λi) is the weight contributing to the interpolation.
10The problem lies in calculating the weights, λ, which will be used in the interpolation. The different methods for computing the weights will be presented in the following sections.
2.1. Deterministic interpolation methods
11Regarding the first group of spatial interpolation methods for measuring rainfall, the most frequently used deterministic methods are the Thiessen polygon (THI) and Inverse Distance Weighting (IDW), which are based on the location of the measured stations and on measured values. In a general way, the forecast of the regionalized value takes into account the weighted average of the observed regionalized values.
12– The simplest and most common spatial interpolation method, particularly in relatively flat zones, is to use the simple average of the number of stations. However, use of this method has decreased because it does not provide representative measurements of rainfall in most cases (Chow, 1964).
13– The Thiessen polygon (THI) method assumes that the estimated values can take on the observed values of the closest station. The THI method is also known as the nearest neighbor (NN) method (Nalder et al., 1998). The method requires the construction of a Thiessen polygon network. These polygons are formed by the mediators of segments joining the nearby stations to other related stations. The surface of each polygon is determined and used to balance the rain quantity of the station at the center of the polygon. The polygon must be changed every time a station is added or deleted from the network (Chow, 1964). The deletion of a station is referred to as “missing rainfall”. This method, although more popular than taking the simple average of the number of stations, is not suitable for mountainous regions, because of the orographic influence of the rain (Goovaerts, 1999).
14– The Inverse Distance Weighting (IDW) method is based on the functions of the inverse distances in which the weights are defined by the opposite of the distance and normalized so that their sum equals one. The weights decrease as the distance increases. This method is more complex than the previous methods, since the power of the inverse distance function must be selected before the interpolation is performed. A low power leads to a greater weight towards a grid point value of rainfall from remote rain gauges. As the power tends toward zero, the interpolated values will approximate the areal-mean method, while for higher levels of power, the method approximates the Thiessen method (Dirks et al., 1998). There is a possibility of including in this method elevation weighting along with distance weighting, Inverse Distance and Elevation Weighting (IDEW). IDEW provides more suitable results for mountainous regions where topographic impacts on precipitation are important (Masih et al., 2011).
15– In the polynomial interpolation (PI) method, a global equation is fitted to the study area of interest using either an algebraic or a trigonometric polynomial function (Tabios et al., 1985). In order to express the polynomial equation in the form of equation (1), the least squares and Lagrange approaches can be used. For more details on this method, see Tabios et al. (1985).
16– The spline interpolation method is based on a mathematical model for surface estimation that fits a minimum-curvature surface through the input points. The method fits a mathematical function to a specified number of the nearest input points, while passing through the sample points. This method is not appropriate if there are large changes in the surface within a short distance, because it can overshoot estimated values (Ruelland et al., 2008).
17– The Moving Window Regression (MWR) method is a general linear regression, which is conducted only in areas where a relationship between the primary and secondary variables is thought to exist (Lloyd, 2005). For example, in applying the MWR method to rainfall, rainfall represents the primary variable and elevation the secondary variable. The rainfall estimation is based on the modeled relationship between the rainfall and elevation data closest to the estimation location.
2.2. Geostatistical interpolation methods
18The second group of spatial interpolation methods for measuring rainfall, geostatistical methods, constitutes a discipline connecting mathematics and earth sciences. Kriging is an example of a group of geostatistical techniques used to interpolate the value of a random field. Matheron (1971) named and formalized this method in honor of Daniel G. Krige, a South African mining engineer who pioneered the field of geostatistics. Kriging is based on statistical models involving autocorrelation. Autocorrelation refers to the statistical relationships between measured points. Not only do geostatistical methods have the capability of producing a prediction surface, but they can also provide some measures of the certainty and accuracy of the predictions.
19In kriging, the value of the interest variable is estimated for a particular point using a weighted sum of the available point observations. The weights of the data are chosen so that the interpolation is unbiased and the variance is minimized. In general, the kriging system must be Linear, Authorized, Unbiased and Optimal (LAUO). Kriging is the first method of interpolation to take into account the spatial dependence structure of the data. There are several types of kriging, which differ according to the form applied to the mean of the interest variable:
20– when it is assumed that the mean is constant and known, simple kriging (SK) is applied;
21– where the mean is constant but unknown, ordinary kriging (ORK) is applied;
22– finally, universal kriging (UNK) is applied where the mean is assumed to show a polynomial function of spatial coordinates. So, in contrast to the other two types, this last type of kriging is not stationary with regard to the mean.
23Stationarity defines itself here by the constancy of the mean, but also by the covariance between two observations that depend only on the distance between these observations. All the different types of kriging apply the stationarity of the covariance, or, more generally, the semi-variogram. This function, which represents the spatial dependence structure of the data, must be estimated and modeled before making the interpolation. First of all, the experimental semi-variogram can be calculated as being half the squared difference between paired values to the distance by which they are separated:
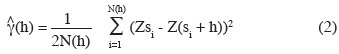
24where N(h) is the number of pairs of data locations at distance h apart.
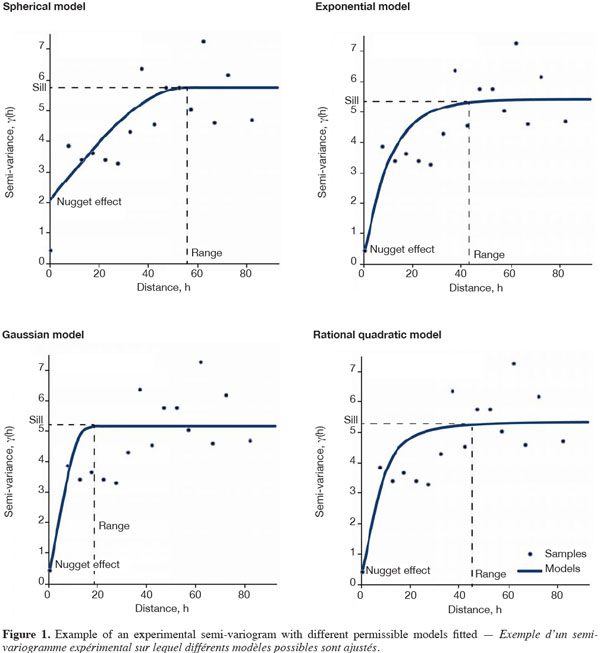
25In practice, the average squared distance can be obtained for all pairs separated by a range of distances and these average squared differences can be plotted against the average separation distance. A theoretical model might then be fitted to the experimental semi-variogram (Figure 1) and the coefficient of this model (nugget effect, sill and range) can be used for a kriging equation system.
26The kriging method encompasses several ways of integrating auxiliary variables:
27– if the mean is not constant, but we can estimate the mean at locations in the domain of interest, then this locally varying mean can be used to inform estimation using SK; this is referred to as Simple Kriging with a Locally varying mean (SKL) (Goovaerts, 2000);
28– Kriging with External Drift (KED) assumes that the mean of the interest variable depends on auxiliary variables; the theory behind KED is in fact the same as the theory behind universal kriging, which also contains a non-constant mean. The drift is defined externally through certain auxiliary variables (Hengl et al., 2003);
29– in order to better meet the assumptions of stationarity, linear regression may be carried out against secondary variables to remove first order trends. The residuals can be used to generate a new variogram and then ordinary kriging can be applied to these residuals. The resulting estimates can be added to the trend to give the estimated values. This technique has been termed Residual Kriging (RK) or Detrended Kriging (DK).
30– the other type of kriging, Ordinary Cokriging (OCK), involves estimating the variable of interest by the weighted linear combination of its observations and the observations of the auxiliary variables. This technique requires the study of the spatial dependence between variables in addition to the study of simple spatial dependences.
31A detailed presentation of geostatistical theories can be found in Cressie (1991); Goovaerts (1997); Chilès et al. (1999) and Webster et al. (2007).
3. Applications and performance of different methods for spatial interpolation of rainfall data
32Studies relating to the interpolation of precipitation often involve a comparison of methods. When a large number of data are available, these comparisons are made by dividing the dataset into two: one set of data for interpolation and the other for validation. This method is ideal because the validation is completely independent of the formulation of the model. Often the data are very few and, in such cases, the comparison of methods is instead made by cross-validation (Isaaks et al., 1990). However, whether the validation is independent or crossed, it allows the identification of errors of prediction. Another way to compare interpolation methods is to use a hydrological model. Here, the interpolated rainfall data can be used as an input into the hydrological model. The observed and simulated discharge can be compared and the error of prediction can be found.
33Spatial interpolation techniques differ in their assumption, deterministic or statistical (geostatistical) nature, and local or global perspective. Deterministic techniques, such as IDW, have been used in numerous studies. Even though IDW is a fairly straightforward deterministic interpolation technique, which offers adaptable weights, the selection of the weighting function is subjective and no measure of error is provided. Therefore, the literature has sought to address questions regarding the bases for the application and further development of multivariate geostatistical techniques, such as KED or cokriging, using various co-variables. It is often recognized that the statistical approach, geostatistical techniques or kriging, present several advantages over deterministic methods. Kriging presents an important advantage in its ability to give unbiased predictions with minimum variance and to take into account the spatial correlation between the data recorded at different rain gauges or weather stations. In addition to providing a measure of prediction error (kriging variance), another major advantage of kriging over simpler methods is that its geostatistical framework is also able to accommodate secondary information in order to improve the interpolation results. For countries with access to satellites, radar, microwave links, etc., the data obtained via these instruments are generally used to improve precipitation interpolation. However, in countries where these modern instruments are not available, measurements of altitude, especially as extracted from a digital elevation model (DEM), form an extensively accessible data source, which can be incorporated into multivariate geostatistical interpolation of rainfall. Nevertheless, some studies have shown that deterministic interpolation methods perform better than geostatistical methods and that the results depend on the sampling density (Dirks et al., 1998). Dirks et al. (1998) compared the performance of IDW, THI and kriging in interpolating rainfall data from a network of thirteen rain gauges on Norfolk Island in all multiple time steps: hour, day, month and year. The results led the authors to recommend IDW for interpolations for spatially dense networks of rain gauges. Most studies have used only daily, monthly or annual time steps for precipitation interpolation. Moreover, some other studies have used only hourly time steps for large-scale extreme rainfall events. Validations in these studies have often been performed using cross-validation methods, although a few other studies have been based on results obtained through hydrological modeling. However, no single method has been shown to be optimal for all time steps and conditions.
3.1. Studies investigating the performance of spatial interpolation methods for annual and monthly rainfall
34Some studies have tested both deterministic and geostatistical methods for interpolating rainfall data. Most of these studies have used only monthly or annual time steps for precipitation interpolation and mapping. There have been many comparative assessments of common interpolation techniques.
35In their study of monthly totals in a large scale network from a 30-year dataset of annual rainfall at 29 stations located in the North Central continental United States, Tabios et al. (1985) found that the statistical methods of kriging and optimal interpolation were superior to other methods. The comparison was based on the error of estimates obtained at five selected sites. The authors found that THI and IDW gave fairly satisfactory results, while PI did not produce good results. In a separate study, Phillips et al. (1992) evaluated three geostatistical methods for making mean annual precipitation estimates on a regular grid of points in the mountainous terrain of the Willamette River basin. Results showed that, compared with ORK, DK and OCK both exhibited better precision and accuracy. In that study, contour diagrams for ORK and DK exhibited smooth zonation following general elevation trends, while OCK showed a patchier pattern more closely corresponding to local topographic features. In another study, Abtew et al. (1993) applied six methods of spatial interpolation over a 4,000 square mile area in South Florida and the results validated historical observations. Results indicated that the multiquadric, kriging, and optimal interpolation schemes were the best three methods for interpolation of monthly rainfall within the study area. The optimal and kriging methods have the advantage of providing the error of interpolation. Nalder et al. (1998) later used four types of kriging and three simple alternatives to estimate 30-year averages of monthly precipitation at specific sites in western Canada. One of the alternatives was a new technique, termed “gradient-plus-inverse distance squared” (GIDS), which combines multiple linear regression and distance-weighting. Based on the mean absolute errors from cross-validation tests, the authors ranked the methods in order of effectiveness for interpolating monthly precipitation as follows: GIDS, OCK, IDW, NN, ORK, DK and UNK. They concluded that GIDS was a simple, robust and accurate interpolation method for use in their region of study, and that it should be applicable elsewhere, subject to careful comparison with other methods. The authors also concluded that it was unfair to use local multiple linear regressions for the relevant stochastic procedure for deterministic methods, but not for geostatistical methods (with the same ancillary variable).
36Basistha et al. (2008) used data from 44 stations to generate a normal annual rainfall map in the Himalayan region of India lying in Uttarakhand state at a 1-km spatial resolution. The authors carried out a comparative analysis by cross-validating interpolation techniques and found that UNK in combination with the hole-effect model (this model relates to the existence of two high valued rainfall fields in the study area) and natural logarithmic transformation with constant trend and the smallest Root Mean Square Error (RMSE) constituted the best choice. That was followed by ORK, spline, IDW and PI. Goovaerts (2000) employed three multivariate geostatistical algorithms (SKL, KED, and OCK) incorporating a digital elevation model for the spatial prediction of rainfall using annual and monthly rainfall observations measured at 36 climatic stations in a 5,000 km² region of Portugal. During cross-validation, the author found that these three multivariate geostatistical algorithms outperformed other interpolators, in particular linear regression, a technique which stresses the importance of accounting for spatially dependent rainfall observations in addition to the co-located elevation. Lastly, Goovaerts (2000) found that ORK yielded more accurate predictions than linear regression when the correlation between rainfall and elevation was moderate. In Great Britain, Lloyd (2005) applied monthly precipitation from sparse point data to a range of interpolation methods: MWR, IDW, ORK, SKL and KED. The MWR, SKL and KED methods relied on elevation data as secondary information. Based on his examination of mapped estimates of precipitation and cross-validation, the author found that KED provided the most accurate estimates of precipitation for all months from March to December, whereas for January and February, ORK provided the most accurate estimates. However, the data for these few months cannot be used to draw accurate conclusions regarding the better performance of a particular technique. The reason for Lloyd (2005) finding KED to be the most accurate precipitation interpolation method from March to December is that, during these months, more neighborhood data were used for interpolation. KED estimates based on a larger neighborhood tend to be more accurate. In another study, Diodato (2005) studied the influence of topographic co-variables on the spatial variability of precipitation using rainfall observations measured at 51 climatic stations in a complex mountainous region of southern Italy (Benevento province). In addition to employing the ORK method, the author added for OCK two auxiliary variables of annual and seasonal precipitation: terrain elevation data and a topographic index. Cross-validation indicated that ORK yielded the largest prediction errors. The smallest prediction errors were produced by a multivariate geostatistical method. Diodato (2005) concluded that OCK is a very flexible and robust interpolation method because it is capable of taking into account several properties of the landscape. More recently, Moral (2010) applied a wide range of geostatistical methods to monthly and annual precipitation data measured at 136 meteorological stations in a region of southwestern Spain (Extremadura). Cross-validation revealed that the smallest prediction errors were obtained for the three multivariate algorithms. In particular, SKL and ORK were found to outperform OCK, which requires a more demanding variogram analysis.
37In the studies described in this section, geostatistical methods were generally found to outperform deterministic methods for spatial interpolation and mapping of monthly and annual precipitation. In particular, the use of multivariate geostatistical methods in combination with elevation data as the secondary variable was generally found to yield the most accurate predictions.
3.2. Studies investigating the performance of spatial interpolation methods for daily rainfall
38Other studies have focused on the use of geostatistical and non-geostatistical approaches for the interpolation of daily rainfall in different sizes of area. There have also been several comparative studies of the performance of interpolation methods used for daily rainfall.
39Employing a geostatistical approach, Creutin et al. (1988) used a rain gauge-radar combination to measure eleven daily events of areal rainfall in the Paris region. An external independent validation indicated that OCK improved slightly the performance of the raw radar data and that the technique exceeded the performance of the classical uniform calibration method. In another study, Beek et al. (1992) selected four days in 1984 in which to investigate the spatial variability in the amount of daily precipitation in north-western Europe in relation to meteorological conditions. Data were interpolated using kriging. Cross-validation showed the occurrence of large differences in the spatial structure of the amount of daily precipitation as a result of different meteorological conditions. Stratification of the study area into a coast, a mountain and an interior stratum proved to be successful, reducing the Mean Squared Error of prediction to a level of 55%.
40Kyriakidis et al. (2001) mapped the seasonal average of daily precipitation for the period from 1 November 1981 to 31 January 1982 over a region in northern California at a 1-km resolution. The study demonstrated the feasibility of constructing realistic analyses of precipitation. The authors integrated readily available and physically relevant predictors, such as atmospheric and terrain characteristics, which control the spatial distribution of precipitation at regional scale. Different interpolation methods were compared in terms of cross-validation statistics and the spatial characteristics of cross-validation errors. Interactions between lower-atmosphere state variables (humidity and horizontal wind components) and terrain (both elevation and its local gradients) provide valuable information for mapping the spatial distribution of orographic precipitation. A geostatistical framework using the maximum amount of relevant atmospheric and terrain information could lead to more accurate representations of the spatial distribution of rainfall than those found in traditional analyses based only on rain gauge data. The magnitude of this improvement in accuracy, however, would depend on the density of the rain gauge stations, on the spatial variability of the precipitation field, and on the degree of correlation between rainfall and its predictors. Classical objective analysis schemes ignore important relevant information such as humidity and vertical wind, and they consequently produce over-smooth representations of the spatial distribution of rainfall; such an adverse effect is intensified when the rain gauge network is sparse.
41Buytaert et al. (2006) studied the variability of spatial and temporal rainfall in the south Ecuadorian Andes using the THI method and kriging with 14 rain gauges in the western mountain range of the Ecuadorian Andes. However, the number of rain gauges in that study was too small to allow the production of an informative variogram using standard estimation (means of the difference between each data pair; see equation 2). Therefore, when data series were available at each point, the experimental semi-variogram produced was calculated in another way, resembling more closely the definition of semi-variance:
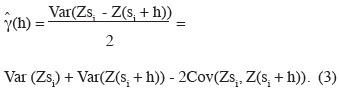
42Cross-validation undertaken by Buytaert et al. (2006) showed that spatial interpolation with kriging provided a better result than the one with THI, and that the accuracy of both methods improved when external variables were included. The external variable integrated into THI referred to data normalization based on the correlation between the mean daily rainfall and the external parameters. The external variable included in the kriging method referred to the UNK process.
43Schuurmans et al. (2007b) performed predictions of point rainfall using ORK and investigated the added value of operational radar for KED and OCK with respect to rain gauges in obtaining a high-resolution daily rainfall field. The spatial variability of daily rainfall was investigated at three spatial extents: 225, 10,000 and 82,875 km², with selected rainfall events. Cross-validation undertaken in the study showed that methods using both radar and rain gauge data (KED and OCK) proved to be more accurate than using rain gauge data alone (ORK), in particular, for larger spatial extents. In a separate study, Carrera-Hernandez et al. (2007) used various forms of geostatistical method to analyze daily climatic data from approximately 200 stations located in the Basin of Mexico for the months of June 1978 and June 1985. The results of cross-validation showed that the interpolation of daily events was improved by the use of elevation as a secondary variable even when that variable showed a low correlation.
44In the studies described in this section, cross-validation of results showed that kriging methods outperformed deterministic methods for the calculation of daily precipitation. However, both types of method were found to be comparable in terms of hydrological modeling results. In the studies described, both elevation and radar data were used in multivariate geostatistical calculations for the daily time step. However, very few methods were compared within any one study.
3.3. Studies investigating the performance of spatial interpolation methods for hourly rainfall
45A small number of studies have considered using hourly time steps for large-scale extreme rainfall events. With specific reference to flood events, Haberlandt (2007) used the combined techniques of KED and indicator kriging with external drift (IKED) for the spatial interpolation of hourly rainfall from rain gauges using secondary variables from radar, daily precipitation within a dense network of rain gauges, and elevation. The methods were performed using data from the storm period of 10th to 13th August 2002, which led to a severe flood event in the Elbe river basin in Germany. Cross-validation carried out in the study showed that the multivariate geostatistical methods KED and IKED obviously outperformed the univariate methods, with the most significant added value being radar, followed by rainfall from the daily network and elevation. The authors found that the best performance was achieved when all secondary information was used at the same time with KED. In some cases, indicator-based kriging techniques give a smaller RMSE than univariate techniques, which use only a single source of information, but this is at the expense of a considerable loss of variance.
46Also focusing on hourly precipitation, Velasco-Forero et al. (2009) compared three geostatistical methods, all incorporating radar data as auxiliary variables in combination with a non-parametric technique to automatically compute correlograms. Cross-validation and spatial pattern analysis showed that KED produced the most accurate results. Schiemann et al. (2011) also used a geostatistical radar-rain gauge combination with non-parametric correlograms and parametric semi-variogram models for the construction of hourly precipitation grids for Switzerland, based on data from a sparse real-time network of rain gauges and from a spatially complete radar composite. In that study, cross-validation showed the KED formulation to be beneficial, particularly in mountainous regions where the quality of the Swiss radar composite was comparatively low. Recently, Verworn et al. (2011) used a multivariate geostatistical approach (KED) for the spatial interpolation of hourly rainfall, using auxiliary topographic data, rainfall data from dense daily networks and weather radar data. The study analyzed certain inundation events occurring between 2000 and 2005 caused by diverse meteorological conditions in northern Germany. Through cross-validation, the authors found that weather radar data were the most useful secondary data for KED for convective summer events, while for the interpolation of stratiform winter events, the use of daily precipitation as secondary data was satisfactory. Generally, the density of rain gauges is usually not sufficient to produce useful variograms on an hourly basis; so the advantage of using a radar estimate lies not only in its ability to give the approximate external variable, but also in the clues it provides regarding the spatial structure of rainfall. The variogram is not given by the reference data (rain gauges) but by the ancillary data.
47In their investigation of hourly rainfall, the studies described in this section focused on large-scale extreme rainfall events. A multivariate geostatistical method (KED) was the one most commonly employed, typically with the incorporation of radar data as the secondary data source. Generally, multivariate geostatistical methods were shown to outperform univariate methods in these studies.
3.4. Validation of interpolation methods using hydrological modeling
48Another way to compare the alternative spatial interpolation methods is to produce and compare various time-series of daily areal precipitation distributions using not only an internal precipitation validation, but also an objective verification based on stream flow simulations (Haberlandt et al., 1998). Haberlandt et al. (1998) used the Mackenzie River Basin in north-western Canada as their study area, carrying out hydrological simulations using the Semi-distributed Land Use-based Runoff Processes (SLURP) model. The authors found that better interpolation techniques and the use of combined precipitation data were able to improve hydrological simulations and that these improvements were related to the relative size of the simulation units used. In a separate study, Ruelland et al. (2008) analyzed the sensitivity of a lumped and semi-distributed hydrological model (Hydrostrahler) to several spatial interpolations of rainfall data. The study was carried out within a context of scarcity of data over a large West African watershed.
49Point by point assessment shows that interpolation using IDW and kriging methods is more efficient than the simple Thiessen technique, and spline, particularly when a monthly time step is used. In fact, spline interpolation can be shown to perform equally as well as the kriging method if the appropriate covariance is used. In other words, a spline estimate with arbitrary parameters will perform in the same way as a kriging technique with an arbitrary variogram. In the study of Ruelland et al. (2008), the use of these data in a daily lumped modeling showed a different ranking of the various interpolation methods with regard to various hydrological assessments. That model seems to be particularly sensitive to the differences in the volume of rainfall input produced by each interpolation method. In fact, the model is calibrated for each rainfall input. Compensation may be built into the model for inadequate rainfall data.
50Recently, Masih et al. (2011) used a semi-distributed hydrological Soil & Water Assessment Tool (SWAT) model to compare that model’s performance under standard precipitation input and modified areal precipitation input obtained through the spatial interpolation Inverse Distance and Elevation Weighting (IDEW) method. The authors concluded that the use of areal precipitation, obtained through interpolation of the available station data, improved SWAT model simulated stream flows. The results were strongly influenced by the spatial extent of the investigations as well as by the station density and spatial distribution of the available rain gauge data used in the interpolation. Moreover, the authors strongly recommended further testing of the SWAT model using areal precipitation as an input obtained through the application of other interpolation methods to rain gauge records. They highlighted the fact that the SWAT model added value to stream flow simulations and other processes. They also suggested that development of an optional component for the interpolation of climatic data within the existing SWAT model would benefit multiple SWAT users. In a separate study, Tobin et al. (2011) presented a comparative analysis of the performance of IDW, ORK, and KED for hourly precipitation fields in complex Alpine terrain. The relevance of the study hinged on the major impact made by inadequate interpolations of meteorological forcing on the accuracy of hydrological predictions regardless of the specifics of the semi-distributed GSM-SOCONT models, during three flood events. The geostatistical methods used relied on a robust anisotropic variogram for the definition of the spatial rainfall structure. Results from cumulative precipitation analysis in the study indicated that IDW tended to significantly underestimate rainfall volumes, whereas ORK and KED methods captured spatial patterns and rainfall volumes induced by storm advection. The use of numerical weather forecasts and elevation data as covariates for precipitation provided evidence for KED outperforming the other methods. Hydrological simulations run with KED-interpolated input fields significantly improved results in terms of specific runoff volume. The model was not re-calibrated with each technique.
51As we have seen in this section, very few studies have focused on comparing the performance of different interpolation methods as evaluated by hydrological modeling. Based on these few studies, the performance of the IDW method can be said to be comparable to that of the ORK method (Ruelland et al., 2008; Masih et al., 2011). KED was not included in these two studies, but this technique demonstrated the best performance in the study of Tobin et al. (2011).
3.5. Use of variogram models and negative weight in geostatistical methods for interpolating rainfall
52Previous studies investigating geostatistical approaches have generally applied the same theoretical variogram model for all time steps. The spherical model has been the one most commonly chosen to interpolate rainfall. Recently, Van De Beek et al. (2011) applied the spherical model in examining the seasonal variogram parameters of daily rainfall in The Netherlands. Similarly, Verworn et al. (2011) applied the spherical model to interpolate hourly rainfall in the northern part of Germany. However, negative interpolated values can occur in kriging (Deutsch, 1996). Once a sample close to the location being interpolated exhibits an outlying value, negative weights in ORK occur. These negative weights can be large, depending on the variogram model and the data values. Moreover, negative weights may produce negative and nonphysical interpolated values when applied to high data values. In general, two approaches can be used to avoid a negative value: a posteriori correction as recommended by Deutsch (1996) or replacing all negative interpolated values with a zero value. Both are realistic solutions, but neither is perfect. Despite the fact that, in some cases, the negative values are large, no study has yet examined this problem.
4. Discussion
53In the literature, the results of the comparison of interpolation methods differ from one study to another. The successful performance of the methods depends on several factors, in particular, temporal and spatial resolutions of the data, and the parameters of the models, such as the semi-variogram in the case of kriging. The studies discussed here focused on the analysis of annual, monthly, daily, hourly or total rainfall for precipitation events of some duration with different densities of observation networks. It is thus difficult to draw a general conclusion. No one interpolation method stands out as being universally the best. Some authors recommend a particular method as being the best according to their judgment as to what is the most practical (Tabios et al., 1985; Abtew et al., 1993; Syed et al., 2003). These authors note all the relatively equivalent levels of performance between the ORK technique and the multiquadratic functions (spline type). However, both Tabios et al. (1985) and Abtew et al. (1993) recommend the use of the ORK technique because it allows the calculation of errors of prediction. On the other hand, Syed et al. (2003) chose to employ the multiquadratic functions because they consider them easier to use. Also, within the context of a dense network of stations, Dirks et al. (1998) did not obtain significant improvements in results by using ORK rather than IDW. They thus recommend the simpler IDW method. In fact, this observation of the better performance of IDW has been extended to its use with other types of data. For example, in an analysis of synthetic data from a computational experiment, Zimmerman et al. (1999) obtained a better interpolation with ORK or with UNK than with the IDW method only when the sampling point was regular, the noise low and the spatial correlation strong.
54Several studies have examined methods of multivariate interpolation. In some studies, radar-rainfall data have been used in combination with measurement at weather stations for spatial interpolation of precipitation (Creutin et al., 1988; Haberlandt, 2007; Schuurmans et al., 2007b; Velasco-Forero et al., 2009). However, the bulk of studies have made use of a cheaper, widely available data source, the Digital Elevation Model (DEM), taking advantage of the relationship between amount of precipitation and elevation. In particular, Phillips et al. (1992); Nalder et al. (1998); Goovaerts (2000) and Lloyd (2005) incorporated elevation into the interpolation of precipitation. These authors mainly used spline, SKL, RK or DK, KED and OCK. These multivariate methods seem to give better results than univariate methods in mountainous regions for a scale of about 10,000 km² (Phillips et al., 1992) or when the correlation between the rainfall data and the elevation is higher than 0.75 (Goovaerts, 2000). It is important to note that all these studies were conducted using annual or monthly precipitation. For finer temporal resolutions, such as a daily resolution, a strong relationship between elevation and precipitation is questionable, according to Haberlandt et al. (1998). Even though these authors observed an average correlation of 0.52 between elevation and the annual accumulation of precipitation, this correlation fell to 0.06 for daily observations. They thus relied more on integration into the interpolation of another auxiliary variable: precipitation simulated by an atmospheric model. Furthermore, these authors studied the interpolation of precipitation within a context of hydrological modeling and used hydrological simulations in addition to cross-validation to compare their tested methods. The only multivariate method that they examined was KED. They applied this method either to all the time steps of their test period, or only when the correlation between the observations of stations and the auxiliary data exceeded a certain threshold (0.5 or 0.3 depending on the auxiliary variable in question). Where the correlation was too low, they used ORK. The authors obtained better results by applying the KED method conditionally rather than by using it for every time step. On the other hand, the indications obtained via cross-validation for the conditional KED were only very slightly better than those for ORK. Furthermore, for the hydrological simulations, it was ORK that gave the best results. Multivariate methods were found to bring an improvement to the quality of the interpolation only when they were used at the right time, but this improvement did not seem to have a great impact on the quality of the hydrological modeling.
55In contrast, Ruelland et al. (2008) found a different ranking of the various interpolation methods used between point by point assessment and hydrological simulation. They found that accurate assessment of the rainfall input volume was more important than the rainfall pattern itself for simulating stream flow hydrographs. They reached this conclusion through the use of a lumped model. This model does not account for the spatial variability of precipitation input with the basin. Masih et al. (2011) found IDEW to be a good method for rainfall input in a semi-distributed SWAT model. However, the authors did not make a comparison between IDEW and any geostatistical methods, which are usually found to be superior to such a simple method. To overcome such limitations, more types of geostatistical methods are currently being tested to prepare hourly rainfall input for hydrological modeling during flood events (Tobin et al., 2011). The use of improved rainfall input in KED provides evidence for increased accuracy in the prediction of discharge volume and peaks.
56For annual and monthly rainfall, geostatistical methods appear preferable particularly, multivariate geostatistical methods which can be beneficial when using elevation data as a secondary variable. On the other hand, for daily rainfall, multivariate geostatistical methods and IDW are in competition. This is probably due to the fact that studies indicating the better performance of IDW were conducted using only one geostatistical method (ORK) and/or other simple methods such as THI and spline, while studies indicating the better performance of multivariate geostatistical methods only made a comparison within the family of geostatistical methods. Some authors have used radar data as a secondary variable, which is normally well correlated with rainfall from rain gauges thanks to the similar nature of the variable. A comparison between common deterministic methods (such as THI and IDW) and different types of geostatistical methods has not yet been made for daily rainfall.
57More recent studies have focused on hourly rainfall rather than on calculating rainfall in other time steps, as in previous studies. These more recent studies have been conducted in developed countries where modern instruments, such as radar, are available. As a result, radar rainfall has always been used in these studies as a secondary variable in multivariate geostatistical analysis (KED and OCK). These two methods have always demonstrated better performance in comparison with other types of geostatistical methods. However, the transposition of these methods (using radar rainfall) to developing countries cannot be made unless modern instruments are installed. This is very costly. Therefore, other cheap data such as elevation should be used as a secondary variable for incorporation into multivariate geostatistical methods.
58Radar rainfall and elevation have generally been used as the secondary variables for integration into multivariate geostatistical methods. Radar rainfall has been found to be beneficial when incorporated into multivariate geostatistical methods in the interpolation of daily and hourly rainfall. Elevation has also provided a major advantage in improving the use of multivariate geostatistical methods for interpolating monthly and annual rainfall. However, very few studies have focused on incorporating elevation into multivariate geostatistical methods for daily rainfall interpolation. The reliability of predictions may vary if a different time step is chosen. The stochastic nature of daily rainfall, in particular, differs from that of monthly or annual rainfall. Therefore, it would be interesting to discover whether integration of elevation as a secondary variable improves interpolation accuracy, because rainfall data are mostly available at a daily time step in countrywide or regional measurements. Daily rainfall is the most important meteorological input into water resources and agricultural modeling systems. The question is whether what constitutes the best technique when applied to monthly or annual rainfall is also appropriate to apply to daily rainfall when precipitation pattern differences exist between daily and monthly timescales.
59Very few analyses have been made of the impact of rain gauge density on interpolation methods. Some studies have focused primarily on the effect of rain gauge density using only one method (ORK, UNK or KED) or two methods (multiquadratic surface fitting and kriging) (Borga et al., 1997). This use of only one or two methods may have been due to the cumbersome nature of the analysis, in terms of computation time. However, given that computational facilities are now better developed and more widely available, it would be interesting to now make a comparison between a wider range of techniques. This might provide some insights in terms of particular strengths, weaknesses and applicability of a variety of methods. Such analyses related to rain gauge density would be valuable for engineers, hydrologists or decision makers working with sparse rain gauge data.
60Solutions to the problem of negative weights in kriging are extremely limited in the method’s application to rainfall. We recommend further investigation into how negative results can be eliminated through using kriging. For example, since negative kriged values may be generated as the result of a chosen variogram model, several variogram models could be used to minimize the risk of negative results appearing. Using a variety of variogram models might avoid negative rainfall calculations.
5. Conclusion
61This article has presented and discussed previous studies related to spatial interpolation of rainfall. The main conclusions drawn here can be summarized as follows:
62– for annual and monthly rainfall, geostatistical interpolation methods seem preferable to deterministic methods. In particular, the use of multivariate geostatistical methods in combination with elevation data has generally yielded more accurate interpolations;
63– for daily rainfall, geostatistical methods and IDW have proved to be comparable approaches, in particular for hydrological modeling. However, very few studies have focused on incorporating the variable of elevation into multivariate geostatistical interpolation of daily rainfall. Moreover, the use of differently interpolated rainfall as an input for hydrological models has been very little studied;
64– most authors have applied radar data as the secondary variable when analyzing hourly rainfall. Studies following this trend have been carried out mostly with multivariate geostatistics (KED) and a few other univariate methods;
65– limited comparison has been made within a study between the use of common deterministic and different types of geostatistical interpolation methods, in particular for daily rainfall;
66– the impact of rain gauge density on interpolation methods has been very little studied.
67The studies reported here have made us strongly aware of the need for further research in order to discover the ways and means to improve the accuracy of rainfall input for hydrological modeling. The investigations undertaken so far have been restricted in numerous aspects, thereby stressing the need for further research. They have, however, provided very useful steps in that direction.
68Quantification and awareness of the uncertainties associated with hydrological data are thus essential for the correct interpretation of the results of the modeling. The precise evaluation of the spatiotemporal variability of rainfall on the watershed scale presents a complex problem because of the small number of rain gauges in most cases and because rainfall is extremely varied in space and time. The choice of interpolation method for measuring rainfall depends on the quantity of valid measures, the nature of the rain in the regions under study and the quality of the observations. The choice of method is therefore crucial. Furthermore, a sensitivity analysis of a hydrological model can be a complementary indicator of the quality of the interpolation of rainfall and of other meteorological parameters. Thus, strategies for the acquisition and the pretreatment of data can be better realized so as to achieve a more efficient hydrological modeling.
69Acknowledgements
70Sarann Ly is financially supported by a scholarship from the cooperation project CUI-ITC01 funded by CUD (Commission Universitaire pour le Développement), Belgium.
Bibliographie
Abtew W., Obeysekera J. & Shih G., 1993. Spatial analysis for monthly rainfall in South Florida. J. Am. Water Resour. Assoc., 29(2), 179-188.
Basistha A., Arya D.S. & Goel N.K., 2008. Spatial distribution of rainfall in Indian Himalayas - a case study of Uttarakhand region. Water Resour. Manage., 22(10), 1325-1346.
Beek E.G., Stein A. & Janssen L.L.F., 1992. Spatial variability and interpolation of daily precipitation amount. Stochastic Hydrol. Hydraul., 6(4), 304-320.
Bell V.A. & Moore R.J., 2000. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci., 4(4), 653-667.
Borga M. & Vizzaccaro A., 1997. On the interpolation of hydrologic variables: formal equivalence of multiquadratic surface fitting and kriging. J. Hydrol., 195(1-4), 160-171.
Buytaert W. et al., 2006. Spatial and temporal rainfall variability in mountainous areas: a case study from the South Ecuadorian Andes. J. Hydrol., 329(3-4), 413-421.
Carrera-Hernandez J.J. & Gaskin S.J., 2007. Spatio temporal analysis of daily precipitation and temperature in the Basin of Mexico. J. Hydrol., 336(3-4), 231-249.
Caruso C. & Quarta F., 1998. Interpolation methods comparison. Comput. Math. Appl., 35(12), 109-126.
Chaubey I., Haan C.T., Grunwald S. & Salisbury J.M., 1999. Uncertainty in the model parameters due to spatial variability of rainfall. J. Hydrol., 220(1-2), 48-61.
Chilès J.P. & Delfiner P., 1999. Geostatistics: modelling spatial uncertainty. 1st ed. New York, USA: Wiley-Interscience.
Chow V.T., 1964. Handbook of applied hydrology: a compendium of water-resources technology. 1st ed. New York, USA: McGraw-Hill, Inc.
Chow V.T., Maidment D.R. & Mays L.W., 1988. Applied hydrology. International ed. Singapore: McGraw-Hill, Inc.
Cressie N., 1991. Statistics for spatial data. 1st ed. New York, USA: Wiley.
Creutin J.D., Delrieu G. & Lebel T., 1988. Rain measurement by raingage-radar combination: a geostatistical approach. J. Atmos. Oceanic Technol., 5(1), 102-115.
Deutsch C.V., 1996. Correcting for negative weights in ordinary kriging. Comput. Geosci.-Uk, 22(7), 765-773.
Diodato N., 2005. The influence of topographic co-variables on the spatial variability of precipitation over small regions of complex terrain. Int. J. Climatol., 25(3), 351-363.
Dirks K.N., Hay J.E., Stow C.D. & Harris D., 1998. High-resolution studies of rainfall on Norfolk Island. Part 2: Interpolation of rainfall data. J. Hydrol., 208(3-4), 187-193.
Goovaerts P., 1997. Geostatistics for natural resources evaluation. New York, USA: Oxford University Press.
Goovaerts P., 1999. Using elevation to aid the geostatistical mapping of rainfall erosivity. Catena, 34(3-4), 227-242.
Goovaerts P., 2000. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol., 228(1-2), 113-129.
Groisman P.Y. & Legates D.R., 1994. The accuracy of United States precipitation data. Bull. Am. Meteorol. Soc., 75(2), 215-227.
Haberlandt U., 2007. Geostatistical interpolation of hourly precipitation from rain gauges and radar for a large-scale extreme rainfall event. J. Hydrol., 332(1-2), 144-157.
Haberlandt U. & Kite G.W., 1998. Estimation of daily space-time precipitation series for macroscale hydrological modelling. Hydrol. Process, 12(9), 1419-1432.
Hengl T., Geuvelink G.B.M. & Stein A., 2003. Comparison of kriging with external drift and regression kriging. Enschede, The Netherlands: ITC.
Isaaks E.H. & Srivastava R.M., 1990. An introduction to applied geostatistics. New York, USA: Oxford University Press.
Johnson G.L. & Hanson C.L., 1995. Topographic and atmospheric influences on precipitation variability over a mountainous watershed. J. Appl. Meteorol., 34(1), 68-87.
Kyriakidis P.C., Kim J. & Miller N.L., 2001. Geostatistical mapping of precipitation from rain gauge data using atmospheric and terrain characteristics. J. Appl. Meteorol., 40(11), 1855-1877.
Lanza L.G., Ramirez J.A. & Todini E., 2001. Stochastic rainfall interpolation and downscaling. Hydrol. Earth Syst. Sci., 5(2), 139-143.
Lloyd C.D., 2005. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. J. Hydrol., 308(1-4), 128-150.
Looper J.P. & Vieux B.E., 2011. An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physics-based distributed hydrologic model. J. Hydrol., 412-413, 114-132.
Mandapaka P.V., Krajewski W.F., Mantilla R. & Gupta V.K., 2009. Dissecting the effect of rainfall variability on the statistical structure of peak flows. Adv. Water Resour., 32(10), 1508-1525.
Masih I., Maskey S., Uhlenbrook S. & Smakhtin V., 2011. Assessing the impact of areal precipitation input on streamflow simulations using the SWAT model. J. Am. Water Resour. Assoc., 47(1), 179-195.
Matheron G., 1971. The theory of regionalized variables and its applications. Paris : École Nationale Supérieure des Mines de Paris.
Moral F.J., 2010. Comparison of different geostatistical approaches to map climate variables: application to precipitation. Int. J. Climatol., 30(4), 620-631.
Nalder I.A. & Wein R.W., 1998. Spatial interpolation of climatic normals: test of a new method in the Canadian boreal forest. Agric. For. Meteorol., 92(4), 211-225.
Nicotina L., Celegon E.A., Rinaldo A. & Marani M., 2008. On the impact of rainfall patterns on the hydrologic response. Water Resour. Res., 44(12).
Obled C., Wendling J. & Beven K., 1994. The sensitivity of hydrological models to spatial rainfall patterns: an evaluation using observed data. J. Hydrol., 159(1-4), 305-333.
Phillips D.L., Dolph J. & Marks D., 1992. A comparison of geostatistical procedures for spatial analysis of precipitation in mountainous terrain. Agric. For. Meteorol., 58(1-2), 119-141.
Refsgaard J.C., 1996. Terminology, modelling protocol and classification of hydrological model codes. In: Abbott M.B. & Refsgaard J.C., eds. Distributed hydrological modelling. Dordrecht, The Netherlands: Kluwer Academic Publishers, 17-39.
Ruelland D., Ardoin-Bardin S., Billen G. & Servat E., 2008. Sensitivity of a lumped and semi-distributed hydrological model to several methods of rainfall interpolation on a large basin in West Africa. J. Hydrol., 361(1-2), 96-117.
Schiemann R. et al., 2011. Geostatistical radar-raingauge combination with nonparametric correlograms: methodological considerations and application in Switzerland. Hydrol. Earth Syst. Sci., 15(5), 1515-1536.
Schuurmans J.M. & Bierkens M.F.P., 2007a. Effect of spatial distribution of daily rainfall on interior catchment response of a distributed hydrological model. Hydrol. Earth Syst. Sci., 11(2), 677-693.
Schuurmans J.M., Bierkens M.F.P., Pebesma E.J. & Uijlenhoet R., 2007b. Automatic prediction of high-resolution daily rainfall fields for multiple extents: the potential of operational radar. J. Hydrometeorol., 8(6), 1204-1224.
Segond M.L., Wheater H.S. & Onof C., 2007. The significance of spatial rainfall representation for flood runoff estimation: a numerical evaluation based on the Lee catchment, UK. J. Hydrol., 347(1-2), 116-131.
Sevruk B., 1997. Regional dependency of precipitation-altitude relationship in the Swiss Alps. Clim. Change, 36(3-4), 355-369.
Shah S.M.S., O’Connell P.E. & Hosking J.R.M., 1996a. Modelling the effects of spatial variability in rainfall on catchment response. 1. Formulation and calibration of a stochastic rainfall field model. J. Hydrol., 175(1-4), 67-88.
Shah S.M.S., O’Connell P.E. & Hosking J.R.M., 1996b. Modelling the effects of spatial variability in rainfall on catchment response. 2. Experiments with distributed and lumped models. J. Hydrol., 175(1-4), 89-111.
Sinclair M.R., Wratt D.S., Henderson R.D. & Gray W.R., 1997. Factors affecting the distribution and spillover of precipitation in the Southern Alps of New Zealand – a case study. J. Appl. Meteorol., 36(5), 428-442.
Singh V.P., 1995. Watershed modeling. In: Singh V.P., ed. Computer models of watershed hydrology. Colorado, USA: Water Resources Publications, 1-22.
Singh V.P., 1997. Effect of spatial and temporal variability in rainfall and watershed characteristics on stream flow hydrograph. Hydrol. Process, 11(12), 1649-1669.
Syed K., Goodrich D., Myers D. & Sorooshian S., 2003. Spatial characteristics of thunderstorm rainfall fields and their relation to runoff. J. Hydrol., 271(1-4), 1-21.
Tabios G.Q. & Salas J.D., 1985. A comparative analysis of techniques for spatial interpolation of precipitation. Water Resour. Bull., 21, 265-380.
Tobin C. et al., 2011. Improved interpolation of meteorological forcings for hydrologic applications in a Swiss alpine region. J. Hydrol., 401(1-2), 77-89.
Van De Beek C.Z., Leijnse H., Torfs P.J.J.F. & Uijlenhoet R., 2011. Climatology of daily rainfall semi-variance in The Netherlands. Hydrol. Earth Syst. Sci., 15(1), 171-183.
Velasco-Forero C.A., Sempere-Torres D., Cassiraga E.F. & Gomez-Hernandez J.J., 2009. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour., 32(7), 986-1002.
Verworn A. & Haberlandt U., 2011. Spatial interpolation of hourly rainfall - effect of additional information, variogram inference and storm properties. Hydrol. Earth Syst. Sci., 15(2), 569-584.
Webster R. & Oliver M.A., 2007. Geostatistics for environmental scientists. 2nd ed. Chichester, UK: John Wiley & Sons.
Zimmerman D., Pavlik C., Ruggles A. & Armstrong M., 1999. An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math. Geol., 31(4), 375-390.
Pour citer cet article
A propos de : Sarann Ly
Univ. Liege - Gembloux Agro-Bio Tech. Soil-Water Systems. Passage des Déportés, 2. B-5030 Gembloux (Belgium) – Institute of Technology of Cambodia. Department of Rural Engineering. Russian Federation Boulevards. PO Box 86. Phnom Penh (Cambodia). E-mail: ly_sarann@itc.edu.kh
A propos de : Catherine Charles
Univ. Liege - Gembloux Agro-Bio Tech. Applied Statistics, Computer Science and Mathematics. Avenue de la Faculté d'Agronomie, 8. B-5030 Gembloux (Belgium).
A propos de : Aurore Degré
Univ. Liege - Gembloux Agro-Bio Tech. Soil-Water Systems. Passage des Déportés, 2. B-5030 Gembloux (Belgium). E-mail: aurore.degre@ulg.ac.be