- Portada
- Volume 18 (2014)
- Numéro 3
- Non-isothermal moisture balance equation in porous media: a review of mathematical formulations in Building Physics
Vista(s): 0 (0 ULiège)
Descargar(s): 0 (0 ULiège)
Non-isothermal moisture balance equation in porous media: a review of mathematical formulations in Building Physics

Notes de la rédaction
Received on October 4, 2013; accepted on March 17, 2014
Résumé
L'équation de bilan d'humidité dans les milieux poreux : synthèse des formulations mathématiques en physique du bâtiment. La compréhension des transferts de chaleur et de masse dans les milieux poreux est cruciale dans de nombreuses disciplines scientifiques. Les modèles mathématiques ont constamment évolué pour se différencier principalement par les potentiels moteurs utilisés pour décrire les flux d'eau, ainsi que par la complexité de la description des phénomènes physiques impliqués. En Physique du Bâtiment, les modèles hygrothermiques (modèles HAM) sont importants pour décrire le comportement des parois et ainsi déterminer leur impact sur le confort intérieur autant que la performance énergétique. L'équation de bilan hydrique peut y être décrite de multiples manières et est fonction du cas étudié et le fait qu'il induise des basses ou hautes teneurs en eau dans les matériaux de construction. Cet article propose une synthèse des différentes formes que peut prendre cette équation dans la littérature scientifique. Nous proposons de partir de l'équation de bilan hydrique physiquement basée, héritée du concept de Volume Élémentaire représentatif et de la description thermodynamique des flux. Celle-ci est ensuite reformulée en utilisant différentes variables d'état principales, offrant une grande variété d'expressions finales qui sont comparées aux modèles disponibles. La démarche offre l'accès à l'ensemble des coefficients de transport secondaires liés au processus de transformation mathématique. Un accent particulier est également porté sur le choix de la fonction de stockage d'humidité et sur son impact sur les formulations finales obtenues.
Abstract
Understanding heat and mass transfers in porous materials is crucial in many areas of scientific research. Mathematical models have constantly evolved, their differences lying mainly in the choice of the driving potentials used to describe moisture flows, as well as in the complexity of characterizing the physical phenomena involved. Models developed in the field of Building Physics (HAM models) are used to describe the behavior of envelope parts and assess their impact on user comfort and energy performance. The water balance equation can be described in many ways; it is a function of the boundary conditions considered and the fact they induce high or low water content in the porous materials used. This paper gives an overview of various formulations for this equation that are found in the Building Physics literature. It focuses first on the physically based formulation of moisture balance, drawing on the Representative Elementary Volume (REV) concept, coupled with thermodynamic flow rates description. This is then reformulated in line with various main moisture state variables offering a wide variety of expressions that are compared with available models. This approach provides access to all secondary transport coefficients associated with the process of mathematical transformation. Particular emphasis is placed on the moisture storage function choice and its impact on the final mathematical formulations.
Tabla de contenidos
1. Introduction
1Heat, air and moisture (HAM) transfers across envelope elements play a crucial role in building performance and durability as well as in user comfort (Fang et al., 1998; Padfield, 1998; Toftum et al., 1999; Adan et al., 2004; Salonvaara et al., 2004; Osanyintola et al., 2006; Mudarri et al., 2007). The ability of porous materials to store and release moisture through capillarity and hygroscopicity effects has an impact on building behavior and can cause damage when not sufficiently controlled. Modeling this complex behavior in multilayered porous walls has become an important research topic in Building Physics and performance analysis.
2Moisture flows in porous media have been studied for a long time in various research fields, including ground water hydrology, agricultural, chemical and petroleum engineering, and drying technologies. The first work on drying modeling described moisture transfers via a diffusion-like equation linking the flow rate to the product of a moisture content gradient and a constant transport coefficient (Sherwood, 1929). At the same time, soil scientists were discovering the importance of capillary action in moisture movement. Contemporary mathematical models have their roots in the work of Philip and De Vries (1957) and Luikov (1966), who were the first to consider the thermal effect on moisture transfer and to separate liquid and vapor flows. At that point, however, the governing equations remained phenomenological because they were inferred from continuous media descriptions in a rather “intuitive” way. Whitaker (1977) rationalized the theory by detailing the gap between microscopic and macroscopic description through the Representative Elementary Volume (REV) concept. Moisture transfer description was thereafter widely discussed and further investigated (Milly et al., 1982; Nielsen et al., 1986; Milly, 1988). The main difficulty remained in accurately describing non-isothermal moisture transfer and determining the transfer coefficients experimentally because of their high dependence on the transfer potentials.
3Initially, all these advances in the understanding of porous media had a limited impact on models in the Building Physics field. Other methods had been developed, mainly to characterize the accumulation of water in walls by vapor diffusion in steady-state conditions (Glaser, 1959). In this context, some authors showed, prematurely, the potential of incorporating external concepts from soil science into Building Physics (Van Der Kooi, 1971; Hall, 1977) and the first building-oriented models incorporating transient heat and moisture transfers with capillarity effects appeared in the 1980s. They were all oriented towards envelope part description in 1D. In the 1990s, the first computer models were commercialized (including Rode, 1990; Künzel, 1995). As the fundamental understanding of the phenomena and computer power have improved, many other models have been developed over the past two decades, with increasing accuracy and capabilities. There is an exhaustive list of available software on the Energy Tools website of the US Department of Energy and in Delgado et al. (2013).
4In reality, there is no unique means of describing moisture transfer in porous building materials. The mathematical expression of the moisture balance equation and its complexity depends on the initial definition of driving potentials for moisture flows, the simplification hypothesis, the chosen dependent variables and the consequent secondary transport coefficients. This diversity is related to the wide variety of building materials, the hygrothermal conditions they face and typical cases studied in the laboratory or in the field. It is obvious that the moisture buffering of a homogeneous sample at ambient temperature is not dominated by the same transport mode and would not require the same assumptions for its description as rain absorption in a composite wall. Traditionally, HAM models were first designed to treat unsaturated problems, whereas soil-dedicated tools were first optimized for near-saturation processes. This explains why their sets of preferred variables often differ. Both model types are now trying to broaden moisture content range description, while also addressing non-isothermal case studies. There is an urgent need for standardization of the mathematical formulation.
5In this paper, we focus on classic non-isothermal, non-hysteretic moisture transfer in a porous medium. Initially, we look at the moisture balance equation derived from the averaging process over a REV, with all moisture fluxes described according to the actual thermodynamic driving potential. No other balance equation is considered here because the emphasis is on moisture transfer characterization. Linking this balance equation with a physically based description of moisture fluxes, we show how different HAM formulations are obtained by reducing the number of variables and further simplifying the mathematical expressions. Several ways of characterizing moisture storage functions are also presented, including temperature effects, which are seldom discussed in Building Physics. The various mathematical expressions presented in this paper could be used to develop models for general numeric computational tools, such as Comsol Multiphysics. Given their inter-operability, these tools have great potential for solving many HAM building problems (Dubois et al., 2013).
2. Physical background and mathematical translation
2.1. Macroscopic modeling
6A porous medium is a heterogeneous system characterized by a complex matter combination: a solid structure whose pores are filled with liquid and gaseous phases. In order to use the traditional continuous Partial Differential Equations (PDEs) formulation to describe the structure’s hygrothermal behavior, it is necessary to make some simplifications by averaging the phenomena and variables over a REV (Whitaker, 1977; Bear, 2013). This creates equivalence between the real dispersed environment and a fictitious continuum. At any point of this new mathematical space are assigned values of the variables and parameters that are actually averaged values over a volume around this local point (Bear, 2013).
7When the porous medium contains multiple fluid phases, as in most cases in Building Physics, it is replaced by the overlap of several fictitious averaged continuums. Each of these continuums is assigned to a phase and fills the entire domain of the porous medium. It can then be described with typical conservation equations for extensive quantities: inner energy and mass. In order to reduce the number of unknowns, some additional information is needed and this is provided by the constitutive equations, which are relationships between the flux densities of the conserved quantities and some driving forces expressed as the gradient of a state variable. These equations are also sometime referred as phenomenological equations (Bear, 2013) because of their dependence on experimental observations. Finally, by assigning a reference velocity from the selected Eulerian point of view, all the flux densities of the conserved quantities can be divided into convective and diffusive flows.
2.2. REV conservation equation
8General assumptions. It is assumed in the following sections that the porous medium Ω⊂R³ is a multiphase system consisting of the solid matrix, a liquid water phase and a gaseous phase, comprising dry air and water vapor. The total gas pressure in the porous media is expressed:

9The following additional assumptions are made for the mathematical developments described in this paper:
10– the material is non-deformable and isotropic; for a non-isotropic material, standard transfer coefficients have to be replaced by tensors;
11– the fluid phases do not react chemically with the solid matrix;
– the moisture content of the material stored as vapor 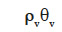 is considered negligible compared with the correspondent term in the liquid phase;
is considered negligible compared with the correspondent term in the liquid phase;
12– the dry air pressure is constant in the material (no air advection) and the total gas pressure gradient is considered negligible;
13– no solid-liquid phase change is considered;
14– there is a local thermodynamic equilibrium between the different phases, which means that water has the same thermodynamic potential in the gaseous, adsorbed and capillary phases;
15– there are no thermal effects caused by friction or compression;
16– the Soret effect is neglected (Janssen, 2011);
17– no hysteresis phenomena are taken into account;
18– no gravity effect is considered.
19The PDE description respects the following general scalar form:

20where u is the dependent variable, F and da are scalar coefficients and Γ is the fluxes vector. The different coefficients can be functions of the spatial independent variables, the dependent variable and the space derivatives of the dependent variable.
21Moisture balance. Equations 3 and 4 show the equations of mass conservation averaged over the REV for the two water phases present in the porous material. Note that in this paper we omit the averaged notation.
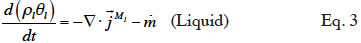
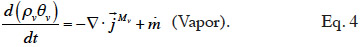
The symbol 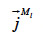 (kg∙m-2∙s-1) is the total mass flux density of liquid water,
(kg∙m-2∙s-1) is the total mass flux density of liquid water, 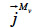 (kg∙m-2∙s-1) is the total vapor mass flux density and
(kg∙m-2∙s-1) is the total vapor mass flux density and 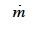 (kg∙m-3∙s-1) is the phase change rate. Since the vapor moisture content is often considered negligible in comparison with liquid moisture content, we can write:
(kg∙m-3∙s-1) is the phase change rate. Since the vapor moisture content is often considered negligible in comparison with liquid moisture content, we can write:

22The two balance equations are added to give the total moisture balance:
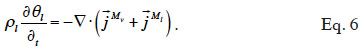
23When assuming negligible total gas pressure gradients in the material, there is no convective vapor flux. Equation 7 shows the resulting balance equation with detailed transport mechanisms:
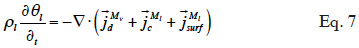
24with the different mass flux densities being
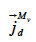 the vapor diffusion,
the vapor diffusion,
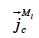 the liquid water transport through capillarity,
the liquid water transport through capillarity,
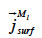 the liquid water transport in the sorbate film (or surface diffusion).
the liquid water transport in the sorbate film (or surface diffusion).
25In a porous system containing a binary mixture of dry air and water vapor under constant total gas pressure, the observed diffusive flow of vapor is a combination of Fick's diffusion, Knudsen diffusion and a transition between both modes, depending on the pore size distribution of the material (Descamps, 1997). As a result, the total vapor diffusion mass flux density can be expressed as:

26where pv (Pa) is the partial vapor pressure and δv (kg∙m-1∙s-1∙Pa-1) is the vapor diffusion coefficient of the material, also called vapor permeability. The latter is a complex function of relative humidity and temperature.
27In an unsaturated porous building material, the liquid water is subjected to the suction of the medium through capillary forces. In a pore, the capillary pressure pc (Pa) represents the difference between gas and liquid pressure over the meniscus:

28This variable is always positive for hydrophilic materials and the liquid pressure is necessarily less than the atmospheric pressure. In Soil Physics, it is common to fix the atmospheric pressure to zero, which results in a negative liquid pressure assuring the continuity with the positive water pressure met in saturated regions under a water column. In unsaturated materials, water is thus subject to a pressure deficit and in order to deal with a positive quantity it is common for soil scientists to define the suction ψ as the negative of the liquid pressure:

29The suction and the capillary pressure are thus rigorously identical and the use of one or the other term is only a matter of choice or scientific habits. The capillary liquid flow rate is then driven by the capillary pressure or suction gradient following Darcy's law and again assuming a negligible total gas pressure gradient:

30with Kl (s) the liquid transfer coefficient (called the “unsaturated hydraulic permeability”; also referred to as “liquid conductivity”). It is important to note that moisture transfers due to capillarity go from low suction (high moisture content, high relative humidity) to high suction (low moisture content, low relative humidity), which is shown through the sign of right hand side of Equation 11.
31The last moisture transport phenomenon to consider is the flow occurring in the liquid film adsorbed on the surface of pores. For building materials under standard operating conditions, multilayer diffusion is expected to prevail because strict monolayer surface diffusion is active only in a very dry state. This transport mode is rather complex and it is particularly difficult to isolate from capillary transport because both phenomena can occur simultaneously in pores of different sizes (Uhlhorn, 1990). The transfer occurs from high to low concentration of adsorbed water, which depends on temperature and relative humidity in a homogeneous material. In HAM models, multilayer diffusion is never featured in detail. In this paper, we take this phenomenon into account through the liquid conductivity function definition, which implies that the temperature effect on multilayer adsorption is not considered. There are more detailed reviews of surface diffusion modeling in Uhlhorn (1990) and Choi et al. (2001).
32In consequence, Equation 12 shows the general moisture conservation equation, with physically based driving potentials:
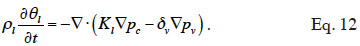
2.3. Closing relationships
33In order to solve the macroscopic balance equation (Equation 12), relationships have to be formulated between the different moisture-related variables (i.e., the moisture content θl, the vapor pressure pv and the capillary pressure pc) in order to limit the number of unknowns. First, as the local thermodynamic equilibrium hypothesis is assumed to be valid about the meniscus in a pore, Kelvin's equation (Defay et al., 1966) relates the capillary pressure to the vapor pressure through relative humidity:
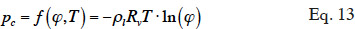
34with the inverse relationship:
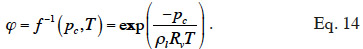
35The Moisture Storage Curve (MSC) of the material provides the second necessary relationship. It is a material-dependent continuous function that expresses the equilibrium moisture content present in the REV for a given thermodynamic humidity condition. The storage process can be expressed in relation to either relative humidity or capillary pressure due to local equilibrium hypothesis. The function is complex to characterize on the whole moisture content range because it is determined mainly by physical adsorption at low moisture content and capillary condensation at high moisture content, with a transition point depending on the pore size distribution of the material, as well as on temperature or hysteresis effects, which alter equilibrium moisture content for a given relative humidity/capillary pressure. As the study of building materials behavior takes root in several scientific fields, the moisture storage functions found in the literature on HAM models take many forms, depending on the moisture content range of interest. They always incorporate adjustable parameters that are either physically based or purely empirical.
Scientists studying low moisture content processes or non-capillary materials often use an isothermal function in the form 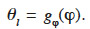 This formulation is common in chemical or food process engineering studies, where the emphasis is on mono- and multilayer adsorption, which are surface phenomena. In this paper we refer to these storage models as “type 1 MSC”. Some of them are semi-empirical g formulations, such as the BET model (Brunauer et al., 1938), whereas others offer a truly empirical g adsorption function, such as the Oswin formulation (Oswin, 1946).
This formulation is common in chemical or food process engineering studies, where the emphasis is on mono- and multilayer adsorption, which are surface phenomena. In this paper we refer to these storage models as “type 1 MSC”. Some of them are semi-empirical g formulations, such as the BET model (Brunauer et al., 1938), whereas others offer a truly empirical g adsorption function, such as the Oswin formulation (Oswin, 1946).
36In contrast, other scientists emphasize the capillary condensation phenomenon linked to high moisture content. Soil scientists, for example, will often use a storage function that is dependent on suction. It is then called the “Moisture Retention Curve” and can be easily expressed as θl = gp(pc). In this paper, this type of formulation is referred to as “type 2 MSC”. Many of these models evolved from the Van Genuchten expression (Van Genuchten, 1980) and offer empirical gp description. Some physically accurate gp functions are based on pore size distribution models. These may themselves be divided into “Bundle of Tubes Models” (Carmeliet et al., 2002; Grunewald et al., 2003) and “Network Models” (Dullien, 1979; Carmeliet et al., 1999). When using a pore-space model, the isothermal moisture retention curve mathematical function is often achievable based on pore-filling theory. There is an example of this approach in Häupl et al. (2003).
37For materials showing mono- and multilayer adsorption as well as capillary condensation, type 1 and type 2 MSCs, with a physically based approach, could be combined by choosing relative humidity or capillary pressure as the thermodynamic potential and performing variable transformations of one of the MSCs using Equations 13 or 14.
The temperature effect on moisture storage is still not perfectly understood, nor has it been studied in detail in Building Physics because it is widely expected to have a minor impact. For some products such as wood-based materials, however, it might play a non-negligible role (Rode et al., 2004). There are several approaches for incorporating thermal effects into moisture storage function description. For hygroscopic-oriented models, the temperature effect is sometimes considered by introducing a temperature dependence of the function parameters or by interpolation on the basis of several individual isothermal curves. This typically gives a direct function in the form 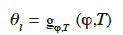 or “type 3 MSC”. According to Poyet et al. (2009), temperature affects equilibrium relative humidity through the Clausius-Clapeyron relationship, which describes the heat involved in the adsorption process. The equilibrium relative humidity dependence on temperature and moisture content is then written thus:
or “type 3 MSC”. According to Poyet et al. (2009), temperature affects equilibrium relative humidity through the Clausius-Clapeyron relationship, which describes the heat involved in the adsorption process. The equilibrium relative humidity dependence on temperature and moisture content is then written thus:
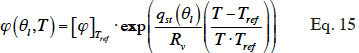
38where qst(J∙kg-1) is the net isosteric heat and the relative humidity at reference temperature is obtained by the inverse of the isothermal sorption function:

Such a 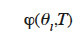 function can be used to obtain different isotherms in order to construct the type 3 MSC interpolation.
function can be used to obtain different isotherms in order to construct the type 3 MSC interpolation.
39In over-hygroscopic and capillary condensation oriented models, it is often assumed that, for a given moisture content, temperature affects equilibrium capillary pressure mainly by modifying water surface tension. Equation 17 provides an example of this approach, as proposed by Milly et al. (1980).
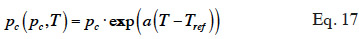
where 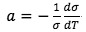 is assumed to be constant.
is assumed to be constant.
40When the temperature-dependent expression of capillary pressure Pc(pc,T) is incorporated into a type 2 MSC with parameters corresponding to reference temperature, it gives a new function:
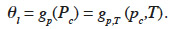
41In this paper, this is referred to as “type 4 MSC”. Again, it is worth noting here that the representation of physical phenomena varies considerably, depending on the original scientific field. In fact, the effect of temperature on moisture storage is a combination of sorption and capillary condensation equilibrium modification. Currently, there appears to be no model that accounts for both effects, another indication of the need for standardization.
2.4. Material moisture transport coefficients
42The liquid conductivity and vapor diffusion coefficient are, in reality, functions of the two chosen dependent variables giving typically non-linear PDEs. In a few particular cases they could be considered as constant parameters, but when large ranges of moisture content or temperature are expected to occur in the material, these simplifications can easily lead to incorrect predictions. As a result, these functions have to be characterized properly when going for so-called “full-range modeling”. There is an example of such characterization in Grunewald et al. (2003), which illustrates the complexity of defining physically based material water transport functions. We do not go into more detail on this subject here because it is beyond the scope of this paper.
3. Formulations according to a main moisture dependent variable
3.1. Method
43We showed how the theoretical moisture balance equation is obtained from a macroscopic description of a porous homogeneous material using the REV concept, with a phase-divided approach. The capillary pressure and vapor pressure emerged as the two physically based driving potentials for the description of water fluxes. The model is based on pressure-driven flows (Funk et al., 2008). As shown by Funk and Wakili (2008), the total moisture flux can be described using the combination of the temperature gradient and one of the main moisture variable gradient. Given that moisture variables are linked together during the transfer process through closing relationships, and assuming local equilibrium, we can perform variable-transformations on each of the constitutive relationships that define liquid or vapor flux (Equations 8 and 11). This is done through partial derivative expressions:
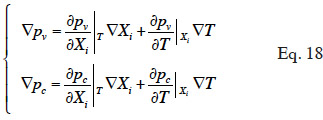
where 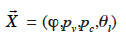 is the main moisture variables vector. We can see immediately that if the main moisture variable is vapor pressure or capillary pressure, there is no need to reformulate the vapor or liquid flux, respectively. In the final stage, the vapor and liquid fluxes can be expressed in the form:
is the main moisture variables vector. We can see immediately that if the main moisture variable is vapor pressure or capillary pressure, there is no need to reformulate the vapor or liquid flux, respectively. In the final stage, the vapor and liquid fluxes can be expressed in the form:
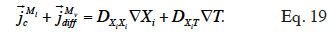
44By developing the balance equation in terms of one or other main moisture state variable, new transport coefficients will arise, DXiXi and DXiT, called “secondary transport coefficients” associated with the gradient of the main moisture variable Xi and temperature T in the Xi-T system, respectively. They are phenomenological functions dependent on the two dependent variables, as well as on primary transport functions. In addition, by choosing a phase-divided approach as a starting point, the vapor and liquid transport sub-functions are easily identified through Equation 18.
45In this paper, the pressure-driven moisture balance equation is re-formulated using two modeling strategies. The first strategy is to choose one of the thermodynamic variables as the main moisture state variable, Xi ≠ θl. In this case, the left hand side of Equation 12 also has to be reformulated through moisture storage functions:
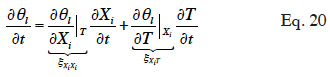
46where ξXiXi is the isothermal moisture capacity of the material (also referred to as specific moisture content in analogy to specific heat) and ξXiT is its non-isothermal moisture capacity. The second strategy is to use the moisture content, which is an empirical variable that can be defined only at REV level. It implies usage limitations of the balance equation obtained. Whenever possible in this paper we highlight the links between the obtained formulations and similar or identical approaches found in the literature on Building Physics models. For each variable choice, mathematical developments are provided in the form of a synthesis table. This table contains the partial derivatives needed for the reformulation, as well as the full mathematical developments of secondary transport functions that might be useful when comparing models. For each strategy and main variable choice, the most commonly used MSCs are mentioned and used to develop the connections between moisture content and thermodynamic variables.
3.2. Strategy 1: thermodynamic variables formulations
47Relative humidity. Table 1 shows the mathematical developments for relative humidity as the main moisture variable, with the most frequent expressions of MSC related to this formulation. Here, only type 3 MSC takes account of the influence of temperature on moisture storage.

The expression of moisture balance with respect to relative humidity is very common in Building Physics research. This moisture field formulation is particularly relevant when modeled phenomena are predominantly in the hygroscopic range or have a simplified liquid transfer characterization. In addition, relative humidity is easily measured with widely used and affordable sensors. The sorption isotherm dependence on temperature is rarely taken into account in software based on 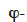 formulation, which almost always uses a type 1 MSC. With this common assumption, the balance equation becomes:
formulation, which almost always uses a type 1 MSC. With this common assumption, the balance equation becomes:
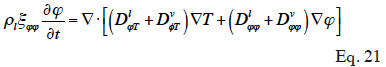
48which is found in Tariku et al. (2010). Künzel (1995) and Künzel et al. (1996) chose to neglect the effects of temperature on liquid transport, i.e.
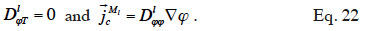
According to these authors, the transport coefficient 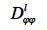 can be derived from wet-cup vapor permeability tests or, more commonly, calculated from the isothermal liquid diffusivity
can be derived from wet-cup vapor permeability tests or, more commonly, calculated from the isothermal liquid diffusivity 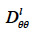 (m2∙s-1), which is the transport coefficient deriving from the moisture content gradient description for liquid transfer (see Strategy 2, Table 4). With this second method, the isothermal liquid transport coefficient is expressed as:
(m2∙s-1), which is the transport coefficient deriving from the moisture content gradient description for liquid transfer (see Strategy 2, Table 4). With this second method, the isothermal liquid transport coefficient is expressed as:

49Without liquid transport, the equation is further simplified (Roels et al., 1999) and finally, in isothermal conditions, it becomes:
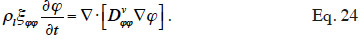
50This simplified balance equation is frequently used for studying isothermal behavior in the hygroscopic region, such as during an MBV experiment (Dubois et al., 2013). It should be noted that the notion of isothermal behavior is purely theoretical because any relative humidity change in the material will result in heat transfer through the latent heat involved in the adsorption process (Hens, 2012). In some cases, however, the simplification can be judged satisfactory.
Vapor pressure. Table 2 shows the development of the moisture balance equation with vapor pressure as the main moisture variable. As the vapor pressure is the thermodynamic variable for vapor diffusion, only the liquid transport and storage terms have to be reformulated. The pv-based formulation, like the 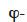 formulation, is more appropriate for describing envelope materials subjected mainly to hygroscopic behavior. The chosen illustration MSC types are therefore the same as for table 1.
formulation, is more appropriate for describing envelope materials subjected mainly to hygroscopic behavior. The chosen illustration MSC types are therefore the same as for table 1.
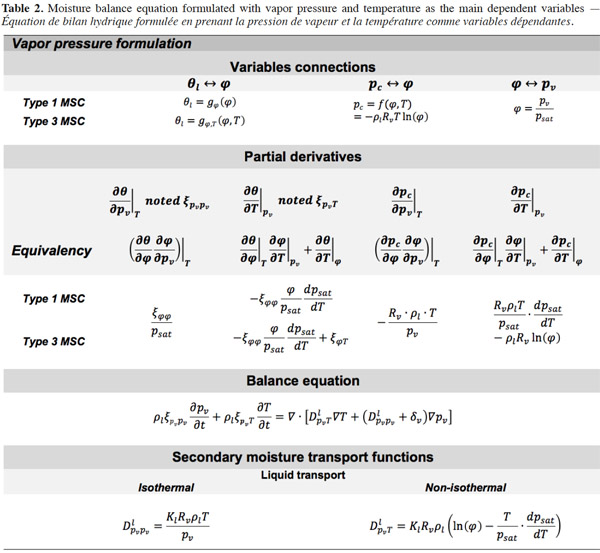
51After the mathematical transformation, the thermal moisture capacity
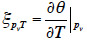
52consists of two distinct parts. One accounts for moisture storage dependence on temperature, the other for the variation of moisture content with temperature at constant vapor pressure because of the moisture storage equilibrium condition with relative humidity. When the temperature increases, as the saturation pressure increases collaterally, the material releases water molecules in the pore space in order to maintain the equilibrium relative humidity value. As a result, with an MSC considered to be independent of temperature, the thermal moisture capacity does not disappear and should be expressed as:

53A similar balance equation was proposed by Dos Santos et al. (2009), with the difference that these authors did not provide the complete mathematical developments of the different partial derivatives. Such transformations have been described by Galbraith et al. (2001), providing a detailed expression of secondary transport functions. Only a type 1 MSC, however, is used there. In Qin et al. (2009), the effect of temperature on vapor pressure equilibrium seemed to be considered erroneously in that the authors did not mention any thermal moisture capacity. Nevertheless, these authors presented an original approach for defining the thermal diffusion coefficient DlpvT as a proper material function and provided an experimental method in order to measure it.
54In isothermal conditions the pv-balance-equation is reduced to:
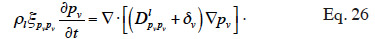
55Galbraith (1992) introduced the concept of differential permeability δ* in order to identify the experimentally liquid and vapor transport function. He wrote:
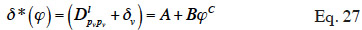
56where A, B and C are constants determined from a set of experiments based on the gravimetric cup test. A review of other mathematical expressions for describing differential permeability is found in Galbraith et al. (1998).
57Capillary pressure. The capillary pressure variable is particularly useful when working with capillary materials in case studies where liquid transport is the main transport mechanism. Such a pc-formulation finds its roots in Soil Physics studies, with Milly et al. (1980) being the first to reformulate the well-known Philip and de Vries equation correctly in terms of capillary pressure head. In Building Physics, capillary-based formulation is fairly unusual and is used by authors who have a particular interest in the near-saturation behavior of materials (e.g., through rain absorption/redistribution or direct soil contact). In this type of research, the hydraulic conductivity and moisture retention functions need to be properly defined in the over-hygroscopic range, which can often be achieved with a pore size distribution model.
58Mathematical developments and the final balance equation in terms of temperature and capillary pressure are shown in table 3. A similar balance equation was formulated by Janssen et al. (2002), who studied the influence of soil moisture on heat losses via the ground. When considering a negligible variation of moisture storage with temperature, the following balance equation is obtained:
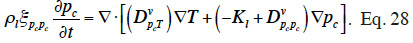
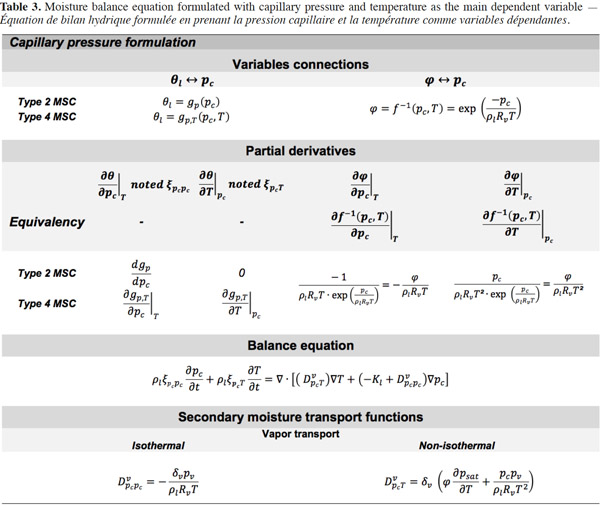
59This expression has been reported by Häupl et al. (2003), Janssen et al. (2007) and Li et al. (2009). These models usually incorporate type 2 MSC, which is illustrated in the synthesis table.
3.3. Strategy 2: moisture content formulation
60Philip et al. (1957) and Luikov (1966) originally chose to develop moisture fluxes according to moisture content and temperature gradients. Moisture content is only an empirical quantity as it cannot be defined at the microscopic scale. Its value is discontinuous across material interfaces, making it an “improper” driving force (Hens, 2012). When studying assemblies of materials at the wall scale, as it is often the case in Building Physics, it is necessary to reformulate the equation using thermodynamic potentials.
61Table 4 provides all the mathematical developments related to moisture balance expression, with moisture content as the main dependent variable. We chose to illustrate the case where the moisture storage function is expressed in relation to relative humidity (i.e., types 1 and 3 MSCs). The main difference with the thermodynamic variable strategy can be seen in the presence of moisture capacity terms inside the moisture diffusivity. Because the relationship between the thermodynamic variables and moisture content depends on the porous material and wetting history, this variable choice could lead to complex expressions of moisture diffusivities. If the hysteresis is taken into account, the transport functions would typically depend on the previous state.

62A moisture balance equation expressed with temperature and moisture content as dependent variables is rare in Building Physics. For constitutive relationships definition, however, some authors choose a hybrid method, where liquid flux is originally expressed as dependent on the moisture content gradient and vapor flux on vapor pressure (Simonson et al., 2004). The liquid transport coefficient is then called “liquid diffusivity”, for which many authors have proposed empirical expressions (Häupl, 1987; Pel, 1995; Krus et al., 1999). For more information on diffusivity approaches, Scheffler (2008) provides a pertinent review. From the mathematical developments shown in table 4, it appears that liquid transfer should be assumed to also be linked to temperature gradient through non-isothermal liquid diffusivity, which is equal to zero only when the MSC is independent of temperature.
63In isothermal conditions, the equation further simplifies into:
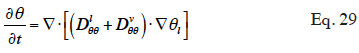
64which should be related to the following, still widely used in research papers:

65The coefficient D (m2∙s-1) is then referred to as “moisture diffusivity”. In this form, the equation has the great advantage of offering an analytical solution through the Boltzmann transformation. It is worth mentioning here the work of Pel et al. (1996), who used this equation and computed the moisture diffusivity function from isothermal water absorption and drying experiments performed at the material sample scale. Such an expression is not valid when a significant temperature gradient is involved because a complex combination of phenomena can hardly be reduced to one unique transport mechanism.
4. Conclusion
66This paper has presented a synthesis of possible moisture balance equation formulations found in coupled heat and moisture transfer models. These tools are intended for the study of porous building materials and can cover a variety of phenomena, sometimes with the focus on the hygroscopic domain and sometimes on the capillary behavior. As a result, they differ in terms of the choice of the main dependent variable and in the levels of simplification that underlie them. All these models are, in fact, rooted in older scientific disciplines that have influenced them in various ways, (e.g., in the choice of moisture storage function expression).
67The work presented began with the physically based balance equation, drawing on the REV concept. Assumptions used covered the frequent non-hysteretic and non-isothermal case without convective transfer. It is clear that the moisture balance equation can be reformulated in many ways. By developing the basic equation in terms of each moisture-related variable, including thermodynamic variables and the moisture content pseudo-variable, we provided an exhaustive list of possible final mathematical formulations. We discussed the moisture storage function in detail and proposed a general classification of models. We showed how temperature can affect thermodynamic equilibrium and how thermal moisture capacities can be expressed depending on the main variable choice. All the secondary transport functions, and their relationship to the two primary functions, vapor diffusion coefficient and liquid conductivity, are available.
68Nomenclature
69DXT: secondary transport coefficient linked to temperature gradient in the equation developed with X as the main moisture variable
70DXX: secondary transport coefficient linked to variable X gradient in the equation developed with X as the main moisture variable
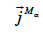 : total mass flux density of the α-phase (kg∙m-2∙s-1)
: total mass flux density of the α-phase (kg∙m-2∙s-1)
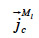 : mass flux density of liquid water through capillary transport (kg∙m-2∙s-1)
: mass flux density of liquid water through capillary transport (kg∙m-2∙s-1)
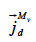 : mass flux density of vapor through diffusion (kg∙m-2∙s-1)
: mass flux density of vapor through diffusion (kg∙m-2∙s-1)
71Kl: liquid water conductivity of the porous material (s)
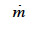 : phase change rate (kg∙m-3∙s-1)
: phase change rate (kg∙m-3∙s-1)
72pc: capillary pressure (Pa)
73psat: saturation vapor pressure (Pa)
74pα: pressure of the α-phase (Pa)
75qst: net isosteric heat (J∙kg-1)
76Rv: specific gas constant for vapor (J∙kg-1∙K-1)
77T: temperature (K)
78δv: vapor diffusion coefficient of the porous material (kg∙Pa-1∙m-1∙s-1)
79δ*: differential permeability (Galbraith, 1992) (kg∙Pa-1∙m-1∙s-1)
80ε: total open porosity of the porous material (-)
81θα: volumetric fraction of the α-phase (m³∙m-3)
82ξXT: non-isothermal moisture capacity in the equation developed with X as the main moisture variable (m³∙m-3∙K-1)
83ξXX: isothermal moisture capacity in the equation developed with X as the main moisture variable (m³∙m-3)
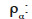 mass density of the α-phase (kg∙m-3)
mass density of the α-phase (kg∙m-3)
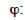 relative humidity (-)
relative humidity (-)
84ψ: suction (Pa)
85Subscripts
86l: liquid
87v: vapor
88g: gaseous
89a: dry air
Bibliographie
Adan O. et al., 2004. Determination of liquid water transfer properties of porous building materials and development of numerical assessment methods: introduction to the EC HAMSTAD project. J. Therm. Envelope Build. Sci., 27(4), 253-260.
Bear J., 2013. Dynamics of fluids in porous media. Dover, UK: Dover Publications.
Brunauer S., Emmett P.H. & Teller E., 1938. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc., 60, 309-319.
Carmeliet J., Descamps F. & Houvenaghel G., 1999. A multiscale network model for simulating moisture transfer properties of porous media. Transp. Porous Media, 35(1), 67-88.
Carmeliet J. & Roels S., 2002. Determination of the moisture capacity of porous building materials. J. Build. Phys., 25(3), 209-237.
Choi J.-G., Do D.D. & Do H.D., 2001. Surface diffusion of adsorbed molecules in porous media: monolayer, multilayer, and capillary condensation regimes. Ind. Eng. Chem. Res., 40, 4005-4031
Defay R. & Prigogine I., 1966. Surface tension and adsorption. London: Longmans.
Delgado J.M., Barreira E., Ramos N.M. & Freitas V.P., 2013. Hygrothermal simulation tools. Hygrothermal numerical simulation tools applied to building physics. London: Springer.
Descamps F., 1997. Continuum and discrete modelling of isothermal water and air transport in porous media. PhD thesis: University of Leuven (Belgium).
Dos Santos G.H. & Mendes N., 2009. Combined heat, air and moisture (HAM) transfer model for porous building materials. J. Build. Phys., 32(3), 203-220.
Dubois S., Evrard A. & Lebeau F., 2013. Modeling the hygrothermal behavior of biobased construction materials. J. Build. Phys., http://jen.sagepub.com/content/early/2013/06/12/1744259113489810, (1st July 2013).
Dullien F.L., 1979. Porous media-fluid transport and pore structure. New York, USA: Academic Press.
Fang L., Clausen G. & Fanger P.O., 1998. Impact of temperature and humidity on the perception of indoor air quality. Indoor Air, 8(2), 80-90.
Funk M. & Wakili K.G., 2008. Driving potentials of heat and mass transport in porous building materials: a comparison between general linear, thermodynamic and micromechanical derivation schemes. Transp. Porous Media, 72(3), 273-294.
Galbraith G.H., 1992. Heat and mass transfer through porous building materials. PhD thesis: University of Strathclyde, Glasgow (United Kingdom).
Galbraith G.H., McLean R.C. & Guo J., 1998. Moisture permeability data: mathematical presentation. Build. Serv. Eng. Res. Technol., 19(1), 31-36.
Galbraith G.H., Li J. & McLean R.C., 2001. Evaluation of discretized transport properties for numerical modelling of heat and moisture transfer in building structures. J. Build. Phys., 24(3), 240-260.
Glaser H., 1959. Grafisches verfahren zur Untersuchung von Diffusionvorgänge. Kältetechnik, 10, 345-349.
Grunewald J., Häupl P. & Bomberg M., 2003. Towards an engineering model of material characteristics for input to ham transport simulations. Part 1: an approach. J. Buil. Phys., 26(4), 343-366.
Hall C., 1977. Water movement in porous building materials. I. Unsaturated flow theory and its applications. Build. Environ., 12(2), 117-125.
Häupl P., 1987. Feuchtetransport in Baustoffen und Bauwerksteilen. PhD thesis: Technische Universität Dresden (Germany).
Häupl P. & Fechner H., 2003. Hygric material properties of porous building materials. J. Therm. Envelope Build. Sci., 26(3), 259-284.
Hens H., 2012. Building Physics. Heat, air and moisture: fundamentals and engineering methods with examples and exercises. Berlin: Ernst & Sohn.
Janssen H., 2011. Thermal diffusion of water vapour in porous materials: fact or fiction. Int. J. Heat Mass Transfer, 54(7), 1548-1562.
Janssen H., Carmeliet J. & Hens H., 2002. The influence of soil moisture in the unsaturated zone on the heat loss from buildings via the ground. J. Build. Phys., 25(4), 275-298.
Janssen H., Blocken B. & Carmeliet J., 2007. Conservative modelling of the moisture and heat transfer in building components under atmospheric excitation. Int. J. Heat Mass Transfer, 50(5), 1128-1140.
Krus M. & Holm A., 1999. Approximationsverfahren für die Bestimmung feuchtetechnischer Materialkennwerte, http://www.hoki.ibp.fraunhofer.de/ibp/publikationen/konferenzbeitraege/pub1_15.pdf, (7 May 2013).
Künzel H.M., 1995. Simultaneous heat and moisture transport in building components. PhD thesis: IRB-Verlag Stuttgart (Germany).
Künzel H.M. & Kiessl K., 1996. Calculation of heat and moisture transfer in exposed building components. Int. J. Heat Mass Transfer, 40(1), 159-167.
Li Q., Rao J. & Fazio P., 2009. Development of HAM tool for building envelope analysis. Build. Environ., 44(5), 1065-1073.
Luikov A., 1966. Heat and mass transfer in capillary-porous colloïdal bodies. In : Actes du colloque international sur les phénomènes de transport avec changement de phase dans les milieux poreux ou colloïdaux, 1966, Paris, France. Oxford, UK: Pergamon.
Milly P., 1988. Advances in modeling of water in the unsaturated zone. Transp. Porous Media, 3(5), 491-514.
Milly P. & Eagleson P.S., 1980. The coupled transport of water and heat in a vertical soil column under atmospheric excitation. Report. Cambridge, MA, USA: Department of Civil Engineering, Massachusetts Institute of Technology, USA.
Milly P. & Christopher D., 1982. Moisture and heat transport in hysteretic, inhomogeneous porous media: a matric head‐based formulation and a numerical model. Water Resour. Res., 18(3), 489-498.
Mudarri D. & Fisk W.J., 2007. Public health and economic impact of dampness and mold. Indoor Air, 17(3), 226-235.
Nielsen D. & Biggar J., 1986. Water flow and solute transport processes in the unsaturated zone. Water Resour. Res., 22(9), 89-108.
Osanyintola O.F. & Simonson C.J., 2006. Moisture buffering capacity of hygroscopic building materials: experimental facilities and energy impact. Energy Build., 38(10), 1270-1282.
Oswin C., 1946. The kinetics of package life. III. The isotherm. J. Soc. Chem. Ind., 65(12), 419-421.
Padfield T., 1998. The role of absorbent building materials in moderating changes of relative humidity. Lyngby, Denmark: Department of Structural Engineering and Materials, Technical University of Denmark.
Pel L., 1995. Moisture transport in building materials. PhD thesis: Technische Universiteit Eindhoven (The Netherlands).
Pel L., Kopinga K. & Brocken H., 1996. Moisture transport in porous building materials. HERON, 41(2), 95-105.
Philip J. & De Vries D., 1957. Moisture movement in porous materials under temperature gradients. Trans. Am. Geophys. Union, 38, 222-232.
Poyet S. & Charles S., 2009. Temperature dependence of the sorption isotherms of cement-based materials: heat of sorption and Clausius–Clapeyron formula. Cem. Concr. Res., 39(11), 1060-1067.
Qin M., Belarbi R. & Ait-Mokhtar A., 2009. Coupled heat and moisture transfer in multi-layer building materials. Constr. Build. Mater., 23(2), 967-975.
Rode C., 1990. Combined heat and moisture transfer in building constructions. PhD thesis: Technical University of Denmark, Lyngby (Denmark).
Rode C. & Clorius C.O., 2004. Modeling of moisture transport in wood with hysteresis and temperature-dependent sorption characteristics. In: Performance of Exterior Envelopes of Whole Buildings IX: International Conference, 2004, Clearwater, Florida. Oak Ridge, TN, USA : Oak Ridge National Laboratory, 2004.
Roels S., Depraetere W., Carmeliet J. & Hens H., 1999. Simulating non-isothermal water vapour transfer: an experimental validation on multi-layered building components. J. Build. Phys., 23(1), 17-40.
Salonvaara M. et al., 2004. Moisture buffering effects on indoor air quality-experimental and simulation results. In: Performance of Exterior Envelopes of Whole Buildings IX: International Conference, 2004, Clearwater, Florida. Oak Ridge, TN, USA : Oak Ridge National Laboratory, 2004.
Sheffler G.A., 2008. Validation of hygrothermal material modelling under consideration of the hysteresis of moisture storage. PhD thesis: Dresden University of Technology (Germany).
Sherwood T., 1929. The drying of solids – I. Ind. Eng. Chem., 21(1), 12-16.
Simonson C.J., Salaonvaara M. & Ojanen T., 2004. Heat and mass transfer between indoor air and a permeable and hygroscopic building envelope: part II–verification and numerical studies. J. Therm. Envelope Build. Sci., 28(2), 161-185.
Tariku F., Kumaran K. & Fazio P., 2010. Transient model for coupled heat, air and moisture transfer through multilayered porous media. Int. J. Heat Mass Transfer, 53(15), 3035-3044.
Toftum J. & Fanger P., 1999. Air humidity requirements for human comfort. PhD thesis: Technical University of Denmark, Lyngby (Denmark).
Uhlhorn R.J.R., 1990. Ceramic membranes for gas separation: synthesis and transport properties. PhD thesis: Universiteit Twente, Enschede (The Netherlands).
Van Der Kooi J., 1971. Moisture transport in cellular concrete roofs. PhD thesis: Technische Hogeschool, Eindhoven (The Netherlands).
Van Genuchten M.T., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J., 44(5), 892-898.
Whitaker S., 1977. A theory of drying. Adv. Heat Transfer, 13, 119-203.