Synthèse bibliographique : le modèle numérique de terrain de haute résolution, ses erreurs et leur propagation

Attached document(s)

Annexes

• pdf (567k)

Résumé

Le modèle numérique de terrain (MNT) est la représentation numérique de la topographie du terrain. C’est une pièce maitresse permettant l’extraction de nombreux paramètres tels que la pente, les axes d’écoulement, etc. Ces paramètres sont régulièrement utilisés comme outils de décision dans la gestion de l’environnement. Dès lors, il est essentiel de générer des MNT exacts d’une part et, d’autre part, de quantifier les erreurs persistantes malgré les corrections et d’estimer leurs impacts sur les paramètres de décision. Cet article présente l’état des connaissances sur la génération de MNT de haute résolution spatiale (maille de dimensions valant ± 1 m). Les technologies d’acquisition des données altimétriques de haute densité (plusieurs points au m²), ainsi que les méthodes de génération du MNT sont présentées et comparées. Les différentes erreurs du MNT ainsi que les méthodes utilisées pour les corriger sont abordées et discutées. Enfin, les méthodes utilisées pour propager les erreurs du MNT dans les applications SIG (Système d’Information Géographique) sont évoquées.

Abstract

The high resolution digital terrain model, its errors and their propagation. A review. The digital elevation model (DEM) is a numerical representation of terrain topography. DEM is a very useful model, allowing the extraction of many parameters such as slope, drainage network, etc. These parameters are regularly used for decision making in environmental management. Therefore, it is very important to generate a reliable DEM, to quantify the errors that remain even after error removal, and also to estimate the impact of these errors on decision parameters. This article presents the current state of knowledge regarding the generating of high resolution DEMs. Fine-resolution (several points per m²) topographic data collection technologies are presented and compared. DEM errors and the methods used to remove them are then highlighted and discussed. Finally, error propagation methods that are used to propagate errors through GIS (Geographic Information System) applications are presented.

Table of content

1. Introduction

1Le MNT (modèle numérique de terrain) est une représentation numérique et mathématique de l’altitude d’un point quelconque de la surface terrestre d’une zone géographique, dans un système référentiel bien défini. Même si le MNT représenté sous forme de triangles irréguliers présente certains avantages (Peucker et al., 1978), dans la grande majorité des cas, le MNT est représenté comme un ensemble de mailles régulières, caractérisées chacune par une valeur d’altitude, dans le but d’en faciliter la manipulation et le stockage en mémoire de l’ordinateur pendant les calculs. Le MNT reste l’une des plus importantes sources de données utilisées pour l’extraction de nombreux paramètres utilisés tels que la pente, la direction d’écoulement de l’eau, l’indice topographique, etc. Cependant, il reste une représentation spatiale de la réalité. Selon Carter (1988), un MNT, même de meilleure exactitude, reste une approximation de la réalité du terrain. Par conséquent, il contient toujours des erreurs. Ces erreurs se propagent inévitablement dans les différentes applications qui l’utilisent et peuvent influencer considérablement les résultats finaux (Huang et al., 2005; Oksanen et al., 2005). La génération d’un MNT nécessite l’acquisition de données spatiales soit sous forme de données altimétriques, soit sous forme de données photogrammétriques. Les moyens d’acquisition de ces données ont beaucoup évolué de nos jours et permettent d’acquérir des données de haute densité (plusieurs points par m²) sur des zones de plusieurs hectares. Dès lors, il est d’une grande importance que nous nous intéressions de près à ces nouvelles technologies, ainsi qu’à l’analyse des erreurs des MNT qui en sont issues afin de les quantifier d’une part et d’autre part, d’identifier les méthodes permettant de les propager à travers une application.

2Cet article passe en revue les différentes étapes de la génération d’un MNT adéquat pour l’extraction de différents paramètres géomorphométriques tels que la pente, la direction d’écoulement de l’eau, etc. L’accent est particulièrement mis sur les nouvelles méthodes d’acquisitions des données altimétriques de hautes densités qui permettent de générer des MNT de haute résolution spatiale1 (maille de dimensions valant ± 1 m) dont la précision altimétrique est de quelques centimètres. Le MNT n’étant pas exempt d’erreurs, nous présentons également les méthodes existantes qui tentent de les propager afin d’analyser leurs impacts sur les résultats des multiples paramètres de décision qui en sont extraits.

2. Acquisition de données altimétriques et génération de MNT de haute résolution spatiale

3Trois techniques d’acquisition de données spatiales nécessaires à la génération de MNT sont utilisées en topographie. Les techniques classiques de positionnement qui sont le tachéomètre électronique, la station totale et le récepteur GNSS (Global Navigation Satellite System) en mode différentiel, les techniques utilisant la technologie de la télédétection (il faut comprendre la télédétection dans sa définition la plus large, c’est-à-dire toute technique permettant l’acquisition d’informations spatiales sur un objet ou un phénomène par l’intermédiaire d’un capteur n’ayant pas de contact avec l’objet étudié (e.g. interférométrie radar, photogrammétrie aéroportée ou satellitaire, LiDAR [Light Detection And Ranging] aéroporté ou terrestre, photogrammétrie à basse altitude utilisant les véhicules non pilotés tels que les microcoptères, les drones, les cerfs-volants, etc.) et les techniques basées sur les informations cartographiques (Nelson et al., 2009). Seules les deux premières peuvent fournir des données de haute densité (plusieurs points par m²) dont la précision des coordonnées dans un système de référence cartographique est de quelques centimètres. Les techniques classiques de positionnement sont néanmoins très contraignantes lorsque la densité des données nécessaires à la génération du MNT est élevée sur une grande zone d’étude (Li et al., 2005). Une comparaison des données sources utilisées pour générer un MNT, faite par Nelson et al. (2009), montre clairement que, par rapport aux autres techniques d’acquisition utilisant la technologie de la télédétection, les données obtenues par photogrammétrie et LiDAR sont celles qui permettent de produire un MNT de résolution spatiale valant quelques dizaines de centimètres avec une précision altimétrique de quelques centimètres. Li et al. (2005) vont plus loin dans la comparaison en considérant, en plus de la précision des données, le temps d’acquisition, le cout et la taille du site de mesure. Le LiDAR et la photogrammétrie apparaissent comme les techniques permettant d’obtenir des données altimétriques de haute densité (plusieurs points par m²) pour générer des MNT de haute résolution spatiale sur des zones de moyennes et grandes superficies.

2.1. Le LiDAR

4Le principe. Le LiDAR (Light Detection And Ranging) est une technique utilisée en télédétection qui exploite les propriétés du laser (Light Amplification by Stimulated Emission of Radiation) pour déterminer les caractéristiques d’un objet distant. Un instrument de mesure utilisant le LiDAR comprend un émetteur, un récepteur de rayon laser et un mécanisme permettant de modifier la trajectoire du rayon laser. Par rapport à un rayon lumineux quelconque, un rayon laser présente un niveau d’énergie, une fréquence et une longueur d’onde bien définis. Dès lors, la comparaison des rayons laser émis et reçus permet d’identifier les caractéristiques d’un objet.

5Les techniques de mesure utilisant le LiDAR peuvent être classées en trois catégories (Heritage et al., 2009a) : les systèmes LiDAR par absorption différentielle utilisés pour mesurer les profils de concentration de gaz dans l’atmosphère, le « LiDAR Doppler » qui mesure la vitesse d’objets en mouvement et les systèmes LiDAR utilisés pour déterminer le positionnement d’un objet en trois dimensions.

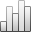
6Le positionnement au LiDAR consiste à partir d’un scanner laser, à envoyer et recevoir un rayon laser sur une cible donnée, à l’instar d’un tachéomètre électronique. Connaissant le temps mis par le rayon, de la cible jusqu’à la source, la distance (d) est mesurée ainsi que l’angle horizontal (φ) et vertical (θ) (Figure 1). Les coordonnées des points mesurés sont ainsi définies dans un repère dont l’origine coïncide avec la source du laser. Les coordonnées tridimensionnelles X, Y et Z sont ensuite calculées (X = d.cos θ.cos φ ; Y = d.cos θ.sin φ ; Z = d.sin θ). Le système opère à une si grande vitesse qu’il permet l’acquisition des coordonnées de plusieurs dizaines voire centaines de milliers de points par seconde.

7Dans la littérature, les scanners utilisés pour le positionnement sont classés en fonction de leur principe de mesure de distance. Les trois grandes catégories sont les scanners laser à impulsion, les scanners laser à mesure de différence de phase et les scanners laser à triangulation. Seulement les deux premières catégories peuvent être utilisées pour l’acquisition de données altimétriques, car leur portée est de plusieurs dizaines de mètres. Les lasers à triangulation sont surtout utilisés pour modéliser des objets de petites tailles. Landes et al. (2011) ont comparé les scanners laser à impulsion et à mesure de différence de phase. Si la cadence de mesure des lasers à impulsion est faible par rapport à celle des scanner laser à différence de phase, ils présentent l’avantage de disposer d’une portée pouvant atteindre 2 000 m, ce qui peut s’avérer très positif pour des mesures d’acquisition de données altimétriques car le nombre de stations nécessaires pour couvrir une zone d’étude donnée (en statique) peut être réduit de manière conséquente.

8De nos jours, les systèmes LiDAR ont la capacité de recevoir un retour multiple du signal émis (tous les systèmes n’en sont pas dotés) et, en général, le système enregistre le premier et le dernier retour du signal (Mallet et al., 2009), ce qui fait du LiDAR une méthode bien adaptée pour analyser la structure des végétations ou pour déterminer le MNT sous un couvert forestier car le dernier retour est celui considéré comme renvoyé par le sol, ce qui n’est pas toujours le cas lorsque la végétation est très dense.

9Les plateformes de mesures utilisées.

10Le LiDAR aéroporté/héliporté. Ces dernières années, le LiDAR aéroporté/héliporté (LiDARa) a été utilisé comme méthode d’acquisition des données altimétriques pour générer des MNT (Bater et al., 2009; Li S. et al., 2011a; Hladik et al., 2012). Le système est composé d’une source de lumière (laser), d’un récepteur GNSS et d’une centrale inertielle. Il consiste à envoyer à partir de la source S (embarqué à bord d’un avion ou un hélicoptère) le rayon laser vers une cible C (e.g. le sol ou le sur-sol) et à déterminer la distance S-C, connaissant le temps de parcours du laser pour revenir vers C (Wehr et al., 1999). À partir des données GPS et inertielles, les coordonnées de la cible sont alors facilement déterminables. Le fait d’embarquer le système dans un hélicoptère permet d’augmenter la densité des points dans des zones spécifiques du site, étant donné que sa vitesse peut être nulle. Le système peut permettre ainsi l’acquisition des coordonnées de 5 000 à 10 000 points par seconde (Nelson et al., 2009). La précision des coordonnées acquises avec le LiDARa dépend de la hauteur de vol. En général, les erreurs sont estimées autour de 15 cm en altimétrie et 50 à 100 cm en planimétrie (Huising et al., 1998; Smith, 2005). Une précision altimétrique inférieure à 15 cm est atteignable si la hauteur de vol est inférieure à 1 200 m ; elle est inférieure à 25 cm, par contre, si la hauteur de vol est comprise entre 1 200 et 2 500 m (Brinkman et al., 2000). Une comparaison complète faite par Baltsavias (1999) montre que, pour une grande partie des applications, le LiDARa est la technologie la mieux adaptée pour l’acquisition des données. La haute densité des points ainsi que la qualité des coordonnées fournies par le LiDARa ont amené certains auteurs (e.g. Nelson et al., 2009) à affirmer que le LiDARa sera la méthode idéale d’acquisition des données dans les prochaines années. Plusieurs pays (e.g. Belgique, Pays-Bas, Suisse, France) disposent de telles données sur leur territoire. Cela est sans doute dû à son cout d’acquisition qui reste son principal désavantage sur de petites surfaces. De plus, depuis quelques années, d’autres méthodes plus adaptées pour des superficies de quelques hectares se sont développées, notamment le LiDAR terrestre (LiDARt) et la photogrammétrie à basse altitude utilisant les véhicules non pilotés. Ces méthodes ne sont pas, à l’heure actuelle, des alternatives au LiDARa qui reste très adapté pour couvrir de grandes superficies. Elles permettent surtout l’acquisition de données altimétriques de grande densité (plusieurs points par m²) avec une précision de quelques centimètres sur des petites zones. Elles présentent l’avantage d’être beaucoup plus abordables et flexibles que le LiDARa en permettant d’atteindre des précisions planimétriques et altimétriques de quelques centimètres (Tahar et al., 2012).

11Le LiDAR terrestre. Le LiDARt peut être fixe (scanner laser statique) ou mobile (scanner laser dynamique) ; dans ce dernier cas, il est alors accompagné des mêmes composantes que le LiDARa, à savoir une centrale inertielle et un récepteur GNSS. Une comparaison des deux systèmes faite par Goulette (2009) dans le cadre d’acquisition de données sur une portion urbaine montre que le système dynamique (plateforme montée sur un véhicule dont la vitesse d’avancement est de 9 km·h^-1) est plus rapide d’un facteur 10. Même si les besoins sont très forts sur le marché, cette étude souligne que les systèmes dynamiques ne répondent que partiellement aux besoins sur la précision des données car celle-ci dépend fortement du système de localisation qui a du mal à garantir une bonne précision des trajectoires du véhicule du fait des multi-trajets, des corridors urbains, des arbres, etc.

12Guarnieri et al. (2009) ont utilisé un scanner à impulsion (Leica HDS 3000) pour l’acquisition des données altimétriques (10 points par m²) dans une zone marécageuse de 3 500 m² occupée par des arbustes dont la hauteur variait de 0,3 à 1 m. Malgré la présence de végétation, leurs résultats montrent que la création d’un MNT de 1 m x 1 m de résolution spatiale est possible, avec un RMSE (Root Mean Square Error) de 3 cm (en condition de végétation peu dense) et une erreur moyenne de 2 cm. Tout récemment, des données LiDARt issues d’un scanner à impulsion (Leica ScanStation) d’une densité de plus ou moins 10 points par m² ont été utilisées par Coveney et al. (2010) comme données de validation d’un MNT de 10 m x 10 m généré à partir de photographies aériennes. Après avoir généré un MNT de 1 m x 1 m de résolution spatiale avec les données LiDARt, leurs résultats montrent que 95 % des erreurs altimétriques sont inférieures à ± 27 cm. Quant à Perroy et al. (2010), en comparant le MNT généré à partir de données LiDARt (acquis en utilisant un LiDARt à impulsion qui est le Riegl LMS-Z420i) avec des levés réalisés à la station totale, ils montrent que le LiDARt surestime les altitudes avec une erreur moyenne de -18 cm et un écart-type de 47 cm. En fonction des conditions, la qualité des données altimétriques obtenues à partir du LiDARt peut donc considérablement varier. Cela est principalement dû aux multiples sources d’erreurs auxquelles l’utilisateur doit prêter attention lors de la réalisation. Cinq erreurs ont été identifiées par Coveney et al. (2011). Il s’agit des erreurs de positionnement des points de contrôle (< 3 cm), des erreurs se produisant lors de la fusion des nuages de points (< 4 cm), des erreurs de géoréférencement (< 5 cm), des erreurs sur les positions du scanner et des cibles (~5 cm) et des erreurs causées par la présence de végétation (~38 cm). L’erreur la plus importante semble donc être causée par la présence de végétation sur la zone d’étude. De plus, cette erreur est d’autant plus importante que l’angle d’incidence (angle entre l’horizontal et la direction du laser) du laser est faible (Kersten et al., 2008). Cela étant principalement dû à la direction rasante du laser lorsque l’angle d’incidence est réduit. Une autre source d’erreur mise en évidence par Kersten et al. (2008) ainsi que Herbin (2012) est la non-verticalité de l’axe du scanner pendant toute la durée de l’opération de mesure. En fonction des caractéristiques de la zone d’étude, le matériel sera plus ou moins stable. On imagine bien que la stabilité sera différente sur un sol labouré ou un sol compacté. La haute densité (centaines de points par m²) des données productibles avec le LiDARt en fait un outil de choix pour la modélisation de la microtopographie du sol. Plusieurs études ont ainsi généré des MNT de quelques millimètres de résolution spatiale à partir de données LiDARt (Eitel et al., 2011; Smith et al., 2011; Barneveld et al., 2013).

13Génération de MNT à partir de données LiDAR.

14Selon Li et al. (2005), avant de générer un MNT à partir d’un nuage de points obtenus sur un site, l’utilisateur doit choisir les critères qui lui permettront d’obtenir le MNT adéquat. En fonction de l’objectif visé, l’utilisateur choisira un critère basé sur la nature de l’élément géométrique utilisé et un critère basé sur le type de données sources. Dans le premier cas, quatre choix sont possibles : la représentation basée sur un élément géométrique de type « point », la modélisation basée sur un élément surfacique triangulaire, la modélisation basée sur un élément surfacique de type rectangulaire et la modélisation utilisant simultanément des éléments surfaciques de type triangulaire et rectangulaire. Dans le second cas, la génération peut utiliser directement (par exemple, construction de mailles triangulaires directement à partir des points mesurés) ou indirectement (utilisation d’une méthode d’interpolation pour créer des mailles régulières à partir des points mesurés) les points originaux.

15La modélisation basée sur un élément géométrique de type point consiste à faire correspondre à chaque point mesuré sur le site d’intérêt, un élément surfacique dont l’élévation correspond à l’altitude du point. Le MNT obtenu se représente alors comme une succession de surfaces planes régulières ou non. La difficulté d’une telle approche se situe au niveau de la définition des limites des éléments surfaciques. La représentation est rendue facile avec des surfaces régulières modélisées en utilisant le diagramme de Voronoi pour caractériser la zone d’influence de chaque point.

16La modélisation basée sur un élément surfacique triangulaire consiste à représenter le MNT par un ensemble de triangles continus dont les sommets correspondent aux points mesurés sur le site. Étant donné que le triangle constitue un élément surfacique élémentaire, cette approche peut être envisagée quelle que soit l’organisation spatiale des points. Les triangles peuvent être réguliers ou irréguliers. L’utilisation de triangles irréguliers est l’approche la plus répandue car les triangles peuvent être générer directement par triangulation à partir du nuage de points obtenu sur le site (Akima, 1978).

17La modélisation basée sur un élément surfacique rectangulaire consiste à représenter le MNT par un ensemble de mailles rectangulaires. Pour des raisons de simplicité, la maille carrée est utilisée en pratique. L’altitude du centre de chaque maille peut être calculée directement par interpolation à partir des points mesurés ou indirectement à partir de triangles obtenus par triangulation (Li et al., 2005). L’utilisation d’une maille rectangulaire présente l’avantage de rendre plus facile la génération du MNT et l’extraction de paramètres géomorphométriques (Hengl et al., 2009). Cependant, l’utilisation d’une maille carrée pour modéliser un terrain complexe avec des ruptures de pente donne un résultat insatisfaisant comparé aux résultats d’une méthode utilisant un élément surfacique triangulaire. Dès lors, ce dernier est plutôt utilisé pour modéliser efficacement (meilleure représentation visuelle) le sursol (arbres, bâtiments, etc.) (Hengl et al., 2009).

18Après une campagne de mesures, la densité des données LiDAR est rarement constante sur l’entièreté du site. Plusieurs raisons en sont la cause. Tout d’abord, les conditions de mesures peuvent entrainer une variabilité de la densité des points et certaines régions (quelques mètres carrés) peuvent n’avoir pas été balayées par le rayon laser. De plus, la présence de bâtiments, de végétation sur le site, etc. agit comme un obstacle qui empêche le rayon laser d’atteindre le sol (Heritage et al., 2009). Dans le cas où uniquement l’altitude des points au sol importe (MNT), l’utilisation d’algorithmes et des traitements manuels permettent la suppression des données. Dans ce dernier cas, la superposition des données à des orthophotographies est nécessaire. Quelle que soit la cause, la création du MNT nécessite de combler l’information altimétrique dans ces régions en utilisant une méthode d’interpolation.

19En SIG (Système d’Information Géographique), l’interpolation consiste à prédire la valeur d’une variable en un point donné en se basant sur les valeurs observées de cette variable sur un nombre déterminé de points localisés dans la zone d’intérêt (Burrough et al., 1998 ; Emery et al., 2000). Ce principe peut être appliqué dans la création d’un MNT lorsqu’il s’agit de déterminer l’information altimétrique manquante. Dans ce cas, la variable d’intérêt est l’altitude et le MNT est généré en estimant l’altitude des points localisés sur une grille régulière à partir d’un ensemble de points dont les coordonnées sont connues. Selon Webster et al. (2007), la plupart des méthodes d’interpolation utilisent l’équation 1 pour prédire la valeur de la variable :

20avec Z* l’estimateur au point u_o de la variable d’intérêt, Z est la variable aléatoire dont la valeur est connue au point u_i, _i est le poids assigné au point observé i et n représente le nombre total de points observés. Il existe de nombreuses méthodes d’interpolation et chacune se distingue par l’application d’une condition qui la définit, e.g. des conditions géostatistiques, des conditions locales, des conditions de lissage et de tension, etc. (Mitas et al., 1999). Le plus souvent, une méthode d’interpolation sera qualifiée de globale ou locale, d’exacte ou inexacte et de déterministe ou stochastique. Une méthode est dite globale si elle utilise toutes les valeurs observées de la variable sur la zone d’intérêt pour prédire la valeur estimée, tandis qu’elle est considérée comme locale si elle n’utilise que les valeurs observées localisées dans le voisinage du point où la variable est estimée. La méthode est exacte si les valeurs observées de la variable sont également celles estimées par la méthode, tandis qu’elle sera considérée comme inexacte dans le cas contraire. Contrairement aux méthodes déterministes, les méthodes stochastiques considèrent la valeur estimée de la variable comme une réalisation parmi d’autres (Burrough et al., 1998; Mitas et al., 1999). Elles incluent donc la notion de probabilité. Une autre classification plus générale adoptée par Li J. et al. (2011) considère trois catégories qui sont : les méthodes géostatistiques, les méthodes non géostatistiques et les méthodes combinant les deux techniques. Ils subdivisent les méthodes géostatistiques en méthodes univariées et multivariées. Les méthodes multivariées utilisent des informations exogènes (e.g. des coordonnées géographiques) en plus des valeurs observées de la variable altimétrique pour réaliser une estimation. Une description détaillée, ainsi qu’une comparaison des différentes méthodes déterministes et géostatistiques sont données dans Li et al. (2008).

21L’utilisation des méthodes d’interpolation pour créer un MNT a fait l’objet de beaucoup de recherches car cette condition a longtemps été une nécessité pour la génération de MNT à partir de données peu denses (< 1 point/m²). Cependant, depuis l’apparition des méthodes d’acquisition des données à haute densité (e.g. le LiDARt), d’autres méthodes ont été utilisées pour générer un MNT à partir de nuages de points très denses (Guarnieri et al., 2009; Coveney et al., 2010). La méthode utilisée consiste à définir une fenêtre f, carrée, de côté fixe R (qui correspondra à la résolution spatiale du MNT créé) et à la mouvoir sur une grille de taille m x n mailles et de pas R. À chaque position ij de f (correspondant à la maille ij), il est alors possible de sélectionner les points du nuage localisés sur la fenêtre. Ensuite, la valeur altimétrique de la maille est déterminée comme une fonction des valeurs altimétriques des points sélectionnés. La fonction utilisée dépendra des objectifs de l’utilisateur. Guarnieri et al. (2009) ainsi que Coveney et al. (2010) et Coveney et al. (2011) ont utilisé la fonction minimum car leur objectif était de déterminer la valeur altimétrique minimale sur un terrain occupé par des cultures. Leur approche assure ainsi une probabilité plus élevée que le point sélectionné, soit sur le sol et non sur les cultures. Pour identifier la taille optimale de R, Guarnieri et al. (2009) ont utilisé des points de contrôle levés au GPS. Ils montrent qu’une valeur de R égale à 1 m est optimale car les erreurs calculées comme étant la différence entre la valeur altimétrique minimale et la valeur altimétrique obtenue au GPS sont minimales. D’autres fonctions peuvent également être utilisées telles que la moyenne, le maximum, le quantile, etc. Certaines de ces fonctions sont disponibles dans la plupart des logiciels de SIG.

2.2. La photogrammétrie

22Le principe. La photogrammétrie est une technique qui permet d’extraire un MNT à partir de couples d’images stéréoscopiques (obtenus, par exemple, à partir des satellites, d’avions, d’hélicoptères ou de véhicules non pilotés, VNP) d’une zone d’étude (Hirano et al., 2003). Le principe est basé sur la reconstruction en trois dimensions d’un objet à partir de la superposition de deux images planes du même objet, perçu sous des angles différents à l’instar de la vision humaine (Aber et al., 2010). L’extraction se fait de manière automatique en utilisant des algorithmes, ce qui nécessite des images numérisées. Ces dernières sont obtenues soit directement en utilisant un appareil photographique numérique ou via une numérisation d’images analogiques. Dans ce dernier cas, l’utilisation de scanners est essentielle. Cependant, pour obtenir des MNT de bonne exactitude, il est nécessaire de réaliser une bonne calibration de l’appareil numérique ou d’utiliser des scanners de haute performance afin de minimiser la distorsion des images (Lane et al., 2000). Selon Fabris et al. (2005), l’extraction d’un MNT par photogrammétrie peut être résumée en trois étapes : l’orientation interne, l’orientation externe et l’extraction des points. L’orientation interne consiste à déterminer le référentiel lié à l’image produite par l’appareil photographique. Par conséquent, certains paramètres importants sont calculés. Il s’agit de la distance focale, des paramètres permettant de modéliser la distorsion de la lentille et de la position du point principal (Aber et al., 2010). Le point principal est l’intersection entre l’axe optique et le plan d’impression de l’image.

L’orientation externe consiste à déterminer les coordonnées (e.g. X, Y, Z dans un système de référence local), ainsi que les angles de rotation 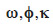de l’appareil photographique par rapport respectivement aux axes du système de référence local au moment de la prise de vue. Ces paramètres peuvent être déterminés en utilisant un GPS et une centrale inertielle embarqués. Cependant, un tel système peut être lourd pour les VNP dont l’utilisation comme méthode d’acquisition de couples stéréoscopiques est de plus en plus répandue (Aber et al., 2010). En plus, l’exactitude du GPS embarqué à bord des VNP est souvent insatisfaisante (Küng et al., 2011). C’est principalement pour ces raisons que la méthode la plus utilisée pour réaliser l’orientation externe consiste à utiliser des points de contrôle levés dans le système de référence local (Aber et al., 2010). Les points de contrôle doivent être matérialisés sur le sol avant l’opération d’acquisition des images car ils doivent être visibles sur celles-ci. L’exactitude des points de contrôle est cruciale pour obtenir un MNT de bonne exactitude. Pour des images de quelques centimètres de résolution (taille des pixels), il est essentiel d’utiliser des points de contrôle très précis, levés par exemple en utilisant une station totale (Aber et al., 2010). En théorie, un nombre minimum de trois points de contrôle sont nécessaires pour déterminer les paramètres de l’orientation externe d’une image. Cependant, en pratique, l’orientation externe est réalisée simultanément pour l’ensemble des couples d’images stéréoscopiques. Cet ensemble d’images est qualifié de bloc d’images et ne nécessite en théorie que quelques points de contrôle pour être orienté. La méthode la plus utilisée pour l’orientation externe est l’ajustement de faisceaux2 (Aber et al., 2010). Le faisceau désigne le segment de droite reliant un point d’attache (points identifiables sur deux ou plusieurs images) ou un point de contrôle sur le sol et son image. L’ajustement de faisceaux consiste à réaliser une orientation des images les unes par rapport aux autres grâce aux points d’attache et ensuite à déterminer les paramètres de l’orientation externe (coordonnées X, Y, Z et orientations 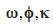de chaque image) et les coordonnées des points d’attache et de contrôle, de telle sorte à minimiser la somme des écarts des faisceaux par rapport aux points d’attache et aux points de contrôle. Il existe différentes méthodes d’identification des points d’attaches. Une énumération détaillée se trouve dans Fabris et al. (2005).

23Les plateformes de mesures utilisées.

24La photogrammétrie aéroportée/héliportée. Elle consiste à équiper un avion ou un hélicoptère d’un appareil photographique digital et à réaliser plusieurs couples d’images stéréographiques de la zone d’intérêt. Le système embarque également une centrale inertielle et un récepteur GNSS qui permettent de déterminer les coordonnées ainsi que l’orientation des photographies. L’obtention d’un MNT de haute résolution spatiale avec des précisions planimétrique et altimétrique centimétriques est cependant conditionnée par l’échelle des photographies (1/30 000 à 1/2 000) et la prise de vue « selon l’axe vertical » des photographies (Henry et al., 2002).

25Pendant des décennies, la photogrammétrie aéroportée a été utilisée dans de nombreuses études pour acquérir des données altimétriques. Mais, ces dernières années, certaines études l’ont décommandé comme moyen d’acquisition des données altimétriques de haute densité du fait de la faible qualité des photographies par rapport à d’autres sources de données (Gooch et al., 1999 ; Henry et al., 2002 ; Fabris et al., 2005). Cependant, les récentes études de Höhle (2009) et de Dehvari et al. (2012) montrent qu’avec les nouveaux appareils photographiques digitaux et les nouveaux algorithmes de traitement, la qualité des MNT générés à partir des photographies aériennes se trouve beaucoup améliorée.

26La photogrammétrie à basse altitude utilisant des véhicules non pilotés (VNP3). La photogrammétrie aérienne à basse altitude utilisant des VNP consiste à équiper un véhicule d’un appareil photographique, à l’instar de la photogrammétrie classique et à réaliser des photographies aériennes à très basse altitude (généralement inférieure à 1 km). Le système peut être semi-autonome ou complètement autonome (Eisenbeiss, 2009). Cependant, de nos jours, les fabricants ont réussi à mettre en place des systèmes à fonctionnements complètement automatisés car la manipulation du véhicule est loin d’être simple (Verhoeven, 2009). Plusieurs types de VNP sont utilisés pour réaliser les photographies à basse altitude. On peut citer de manière non exhaustive les parapentes motorisés (Jütte, 2008), les dirigeables (Gonzalez-Aguilera et al., 2009), les cerfs-volants (Aber et al., 2002), les ballons (Fotinopoulos, 2004), les VNP à voilure rotative (Zhang, 2008 ; Niethammer et al., 2010), les VNP à voilure fixe (Haala et al., 2011 ; Küng et al., 2011). Actuellement, les modèles les plus commercialisés sont surtout les VNP à voilure tournante et les VNP à voilure fixe. Certaines compagnies ont développé des systèmes complètement autonomes permettant à un utilisateur non expérimenté de pouvoir les utiliser. La majorité de ces produits sont à très faible cout par rapport à la photogrammétrie classique (Eisenbeiss, 2009). Les photographies aériennes peuvent alors être utilisées pour créer des orthophotographies, des modèles numériques de surfaces (MNS), des MNT. Cependant, l’un des problèmes majeurs des VNP est l’absence à leur bord d’un système de communication qui permettrait à l’autorité locale du trafic aérien de détecter leur présence (Eisenbeiss, 2009). Par conséquent, les vols de VNP sont contrôlés et leur utilisation nécessite souvent des certificats de vols. Plusieurs études menées ces dernières années ont montré que des MNT/MNS de haute résolution spatiale (dimensions de la maille ≤ 1 m) et de précision altimétrique de quelques centimètres sont productibles à partir des images aériennes à basse altitude (Schiefer et al., 2007). Eisenbeiss et al. (2006) ont utilisé un LiDARt (Riegl LMS-Z420i) et un VNP à voilure rotative pour produire respectivement des MNS de 5 cm et 10 cm de résolution spatiale du site archéologique classé Pinchango Alto. Leurs résultats montrent que les données LiDARt sont limitantes lorsque la topographie du lieu présente des « trous » car ceux-ci ne sont pas « perçus » par le laser. Quant aux données VNP, ce sont plutôt les structures verticales qui sont mal représentées. Cependant, la comparaison des deux modèles montre une différence altimétrique moyenne inférieure à 1 cm et un écart-type de 6 cm. Un si grand écart-type est expliqué par les auteurs comme étant dû au changement brusque de pentes dans certaines parties du site. Malheureusement, cette étude ne donne pas des résultats relatifs à une comparaison par rapport à des données de référence telles que des données GPS en mode RTK (Real Time Kinematic). Cette comparaison est faite par Vallet et al. (2011) avec des données LiDARa et des données obtenues à partir de photographies réalisées avec le Swinglet. En plus, ils ont expérimenté les résultats de deux MNSs générés à partir de deux logiciels commerciaux de traitements de données photogrammétriques : Pix4D (http://www.pix4d.com) et SocetSet NGATE (http://www.socetgxp.com). Leurs résultats montrent des différences moyennes par rapport aux données altimétriques GPS de 0,7 cm (LiDARa), 4,7 cm (Pix4D) et 11 cm (SocetSet NGATE) et des écarts-types respectifs de 4 cm, 9,5 cm et 26,7 cm. Les données LiDARa ont une meilleure exactitude. Nous pouvons remarquer qu’il existe une différence significative entre les résultats obtenus à partir des deux logiciels commerciaux. La différence altimétrique moyenne obtenue à partir de NGATE est deux fois supérieure à celle obtenue à partir de Pix4D. L’écart-type obtenu avec NGATE est trois fois supérieur à celui obtenu avec Pix4D. La méthode de traitement des données a donc un impact non négligeable sur l’exactitude du MNT. Küng et al. (2011) ont également utilisé le Swinglet pour l’acquisition de photographies aériennes à basse altitude. Ils montrent que l’exactitude des données altimétriques est dépendante de la taille des pixels et qu’elle varie entre 2 cm et 20 cm ; elle est supérieure lorsque la texture des images n’est pas appropriée et lorsque la zone présente des discontinuités. Ils soulignent qu’une telle exactitude n’est atteinte qu’à condition d’utiliser des données GPS RTK positionnées indépendamment sur la zone d’étude comme information de géoréférencement et pas les données fournies par le GPS embarqué sur VNP.

27Génération de MNT en photogrammétrie

28Après l’acquisition des photographies aériennes, l’étape suivante consiste à déterminer l’altitude de chaque pixel. Pour un pixel donné sur une image, il s’agit de déterminer le pixel homologue sur l’image avec laquelle un couple stéréoscopique est définissable. Les algorithmes de mise en correspondance peuvent être classés en deux principaux groupes : les algorithmes de type « area-based » et les algorithmes de type « feature-based » (Fabris et al., 2005 ; Aber et al., 2010 ; Gruen, 2012). Les algorithmes qualifiés de « area-based » utilisent une fenêtre centrée sur chaque pixel et réalisent la mise en correspondance par comparaison de l’information (e.g. niveau de gris) disponible au niveau des pixels de la fenêtre (Gruen, 2012). Les algorithmes de type « feature-based » réalisent la mise en correspondance en deux étapes. Une première étape permet de déterminer les formes caractéristiques présentes dans la première image. Ces formes sont principalement dues à la variation d’intensité dans l’image. Ensuite, une deuxième étape consiste à réaliser la comparaison des formes caractéristiques avec celles de la deuxième image. Cette approche considère que les caractéristiques de l’image sont moins variables d’une image à l’autre (Gruen, 2012). Cependant, certaines informations peuvent être perdues après la première étape ; toute l’information n’est donc pas exploitée, ce qui est un désavantage. La qualité du MNT extrait à partir d’un modèle stéréoscopique dépend principalement de la nature de la surface modélisée, des caractéristiques propres aux images utilisées, telles que le contraste et le niveau de bruit, et des paramètres propres aux algorithmes (Aber et al., 2010 ; Gruen, 2012).

29Les algorithmes de type « area based » sont les plus utilisés en photogrammétrie (Gruen, 2012). Ils considèrent l’hypothèse que la distance séparant chaque pixel localisé dans la fenêtre et l’appareil photographique est constante, ce qui n’est pas vérifié sur des terrains inclinés ou avec des variabilités topographiques importantes. Certains auteurs ont proposé différentes améliorations (e.g. Zabih et al., 1994 ; Hirschmüller et al., 2002 ; Scharstein et al., 2002) tout en gardant l’approche « fenêtre ». D’autres auteurs, tels que Hirschmuller (2008), considèrent qu’il faut abandonner l’approche « fenêtre » et utiliser une comparaison pixel par pixel. L’algorithme « semi-global matching » proposé par Hirschmuller (2008) tient compte également de l’écart radiométrique (dû par exemple à l’effet de vignette, au temps d’exposition, etc.) pouvant exister entre deux images stéréoscopiques. Ses performances ont été évaluées de manière satisfaisante (précision altimétrique de 15 cm et une résolution spatiale de 5 cm) par Gehrke et al. (2010) qui ont comparé un MNT généré en utilisant le « semi-global matching » et un MNT généré à partir de données LiDAR. Le désavantage de l’algorithme « semi-global matching » est son temps de calcul élevé lorsque le nombre de photographies aériennes est important (e.g. en photogrammétrie utilisant un VNP). Cette contrainte devient inexistante lorsque le calcul est implémenté sur un GPU (Graphical Processing Unit).

3. Les erreurs du MNT

30Les sources d’erreurs du MNT sont variées et incluent principalement l’exactitude des points de contrôle, la densité et la distribution des données sources, la situation géographique de la zone d’étude, les méthodes utilisées pour générer le MNT et la microtopographie de la zone d’étude (Li, 1991 ; Heritage et al., 2009b). Pike (2002) identifie trois types d’erreurs (différence entre la valeur altimétrique d’une maille et la valeur réelle observable sur le terrain) dans les MNT : les erreurs systématiques, les erreurs aléatoires et les fautes. Les erreurs systématiques résulteraient du processus de génération du MNT et peuvent être éliminées ou réduites si leurs sources sont identifiées. Les fautes résulteraient des erreurs commises lors de la collecte des données. Elles sont identifiables et éliminées normalement pendant les phases de traitement des données avant leur utilisation. Les erreurs aléatoires du MNT sont cependant inévitables. Selon Aguilar et al. (2010), en condition de zones dégagées, l’erreur sur un MNT peut se calculer via la variance donnée par l’équation 2 :

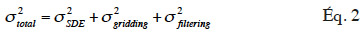
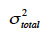exprime l’erreur verticale dans le MNT, 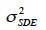exprime l’erreur aléatoire due à l’acquisition des données, 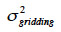exprime l’erreur due à l’interpolation et 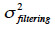exprime l’erreur due au processus de traitement des données. Cependant, sur une zone dégagée, ils considèrent que 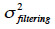peut être négligée, en raison de l’absence d’objets endogènes. 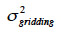peut également être négligée si la densité des points acquis est suffisamment élevée, ce qui est le cas si l’on utilise le LiDAR ou un VNP. Dans ce cas, la variance totale est calculée en utilisant un nombre suffisant de points de contrôle levés sur le terrain avec une précision meilleure que celle des données utilisées pour générer le MNT.

31Cependant, le RMSE4 (équation 3) reste le paramètre utilisé pour quantifier les erreurs d’un MNT.

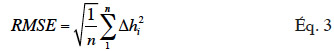
avec 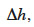la différence d’altitude entre un point de contrôle dont l’altitude est mesurée avec un récepteur GNSS et la maille correspondante sur le MNT. En plus de ce dernier, il est intéressant parfois d’estimer également l’erreur moyenne et l’écart-type des erreurs. Les MNT produits à partir des données altimétriques contiennent toujours des erreurs aberrantes, même si elles ont fait l’objet de traitement. Une manière de supprimer les erreurs aberrantes est d’appliquer un filtre sur les données. L’un des filtres les plus utilisés se base sur le calcul initial du RMSE (Höhle et al., 2006). Alors, toutes les erreurs supérieures à trois fois le RMSE sont considérées comme aberrantes et sont remplacées par une valeur estimée à partir des altitudes des mailles voisines. Une autre approche pour éliminer les erreurs aberrantes, définie par Daniel et al. (2001), considère à la place du RMSE, l’écart-type des données altimétriques initiales. Cette dernière méthode sera surtout utilisée lorsqu’il n’existe pas de points de contrôle ou lorsque leur acquisition est rendue difficile par l’inaccessibilité de la zone d’étude. C’est principalement le cas lorsque la zone d’étude se retrouve en zone forestière. Les erreurs sont d’autant plus importantes que la zone d’étude se situe en milieu non-ouvert, comme dans des forêts ou des zones endogènes. Leur normalité n’est donc pas toujours acceptée. Pour identifier les erreurs aberrantes, Felicisimo (1994) propose de comparer la valeur altimétrique de la maille avec celle estimée à partir de ses voisines. Il définit ainsi pour la maille i une valeur

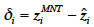
où 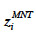est l’altitude de la maille i après création du MNT et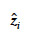

est l’altitude de la maille i, estimée à partir de l’altitude de ses voisines. En considérant 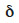comme une variable aléatoire, il est possible de déterminer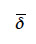

et 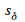qui sont respectivement la moyenne et l’écart-type. En faisant l’hypothèse que 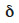a une distribution normale, Felicisimo (1994) réalise un test qui permet d’accepter ou de rejeter l’appartenance de 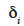à la distribution normale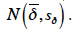

Le test proposé est un test de Student puisqu’il est appliqué individuellement à chaque valeur 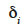(Dagnelie, 2006). L’hypothèse nulle est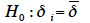

(hypothèse alternative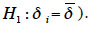

32La valeur

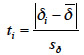
est calculée et comparée à la valeur critique 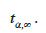Selon Felicisimo (1994), la valeur de 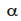doit être choisie la plus faible possible pour détecter uniquement les valeurs élevées de 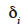Cependant, une valeur élevée n’indique pas nécessairement une erreur, mais cela peut être considéré comme une alarme. 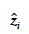peut être estimé tout simplement comme la moyenne des altitudes des mailles voisines (Felicisimo, 1994) ou en utilisant un estimateur plus complexe comme le krigeage, ce qui permet de tenir compte de la variabilité spatiale du terrain (Hengl et al., 2004). La valeur de 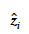est influencée par le nombre de mailles voisines considérées. En général, des fenêtres de 3 x 3 ou 5 x 5 centrées sur la maille i sont utilisées (Hengl et al., 2004), ce qui implique un nombre de mailles voisines valant respectivement 8 ou 24. Cependant, plus le nombre de mailles voisines augmente, plus le temps de calcul est élevé, spécifiquement dans le cas du krigeage. Lorsque l’hypothèse nulle est rejetée (z_i^MNT considérée comme une erreur) est remplacée par 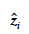(Felicisimo, 1994).

4. Propagation des erreurs du MNT

33Le MNT a plusieurs sources d’erreurs (Li, 1991 ; Heritage et al., 2009b). Huang et al. (2005) ainsi que Oksanen et al. (2005) ont montré que ces erreurs peuvent se propager et influencer considérablement les résultats finaux d’une application. Pour analyser l’impact des erreurs du MNT sur les résultats d’une application (e.g. extraction des axes de ruissellement, calculs de pentes, etc.), il est impératif de les propager à travers les différentes opérations de l’application. Deux principales approches existent pour analyser la propagation des erreurs dans une application, il s’agit de la méthode du développement en série de Taylor et de la méthode de Monte Carlo (Burrough et al., 1998). Cependant, la méthode de Monte Carlo reste la plus utilisée à ce jour en raison de sa simplicité et de sa rigueur (Burrough et al., 1998 ; Wechsler, 2007). De plus, lorsque l’application est le résultat d’une succession d’opérations complexes n’utilisant pas les opérateurs « +, -, ×, ÷ », la méthode du développement en série de Taylor devient presque impossible à programmer (Hengl et al., 2010).

34La méthode de Monte Carlo considère le MNT comme une réalisation parmi d’autres (Wechsler, 2007). Par un processus stochastique, elle simule une valeur d’altitude probable pour chaque maille du MNT. Lorsque le processus est répété plusieurs fois pour toutes les mailles, on observe alors des réalisations probables du MNT (Burrough et al., 1998).

35D’une part, une valeur d’altitude attribuée à une maille du MNT peut être représentée par la somme d’une constante et d’une variable aléatoire d’erreurs altimétriques dont la fonction de distribution est déterminable (Temme et al., 2009). Cette approche est qualifiée d’empirique car la connaissance des erreurs altimétriques nécessite l’utilisation de plusieurs points de contrôle d’une grande précision, positionnés par exemple en utilisant un récepteur GNSS topographique (Wechsler, 2007). D’autre part, en l’absence de points de contrôle (l’acquisition des points de contrôle peut être couteux, voire impossible dans certaines conditions), comme c’est souvent le cas, on utilise l’approche heuristique qui consiste à faire une hypothèse sur la distribution des erreurs altimétriques (Oksanen et al., 2005; Wechsler, 2007). La distribution la plus utilisée est la distribution gaussienne de moyenne nulle et d’écart-type valant l’écart quadratique moyen (EQM) du MNT, car c’est le paramètre le plus souvent disponible pour estimer la qualité d’un MNT.

36La méthode de Monte Carlo tient compte de l’autocorrélation des erreurs altimétriques. Elle peut être simulée par au moins quatre différentes techniques qui sont :

37– le recuit simulé (Fisher, 1991) ;

38– le modèle spatial autorégressif (Goodchild et al., 1992b) ;

39– le modèle moyennes mobiles spatial (Oksanen et al., 2005) ;

40– la simulation séquentielle gaussienne (Goovaerts, 1997).

41La méthode de simulation, qui reste de loin la plus utilisée, est la méthode séquentielle gaussienne de par sa simplicité (Temme et al., 2009).

La méthode séquentielle gaussienne est une méthode géostatistique qui considère que la distribution des erreurs du MNT est normale (Aerts et al., 2003). Elle consiste à visiter chaque maille du MNT et à simuler, pour chacune, une valeur de la variable aléatoire caractérisant les erreurs du MNT en utilisant une distribution de probabilité conditionnelle. Pour la première maille, il s’agit de générer une valeur de l’erreur altimétrique à partir de la distribution normale N 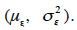Pour la seconde maille, le krigeage simple est utilisé pour générer l’erreur altimétrique, connaissant la valeur de l’erreur altimétrique de la première. Le processus est ainsi répété jusqu’à ce que toutes les mailles soient visitées. L’utilisation du krigeage simple nécessite de connaitre l’autocorrélation des erreurs altimétriques. Dans le cas de l’approche empirique, l’autocorrélation, i.e. le variogramme ou le corrélogramme, est estimée directement à partir des écarts altimétriques entre les points de contrôle et le MNT (Temme et al., 2009). Dans l’approche heuristique, le manque d’information sur les erreurs altimétriques nécessite de faire des hypothèses sur le modèle d’autocorrélation (e.g. exponentiel, gaussien, sphérique, etc.).

42L’un des désavantages de la méthode de Monte Carlo, signalé par Burrough et al. (1998), est le temps de calculs car la méthode qualifiée de « force brute » nécessite un temps important puisque le processus est répété plusieurs fois. De nos jours, avec le développement de la technologie informatique, la puissance des CPU (Central Processing Unit) a beaucoup augmenté d’une part et, d’autre part, des techniques de calculs telles que le calcul distribué sur grille ou le GPU (Graphical Power Unit) sont disponibles et ont été expérimentés par plusieurs auteurs (Niewinski, 2004 ; Ukkonen et al., 2008 ; Wallis et al., 2009). Plusieurs études ont utilisé la méthode de Monte Carlo pour analyser l’impact des erreurs du MNT sur différentes applications (Goodchild et al., 1992a ; Heuvelink, 1998 ; Oksanen et al., 2005; Lindsay, 2006 ; Delbari et al., 2009 ; Hengl et al., 2010 ; Achour et al., 2012). Même si des techniques permettent de limiter le temps de calculs, l’utilisation de la méthode de Monte Carlo se base sur le choix d’un nombre minimal N de réalisations du MNT. N doit être suffisamment grand pour permettre d’atteindre des résultats stables des paramètres calculés sans augmenter inutilement le temps de calcul. Plus N est grand, plus les résultats sont précis. Cependant, cette précision est proportionnelle à la racine carrée de N, i.e. pour doubler la précision, il faut quadrupler N (Temme et al., 2009). Le nombre de réalisations N nécessaires pour obtenir des résultats stables diffère selon le type d’applications (Heuvelink, 1998 ; Lindsay et al., 2005 ; Oksanen et al., 2005 ; Hengl et al., 2010). Toutefois, Heuvelink (1998) ainsi que Burrough et al. (1998) signalent que N doit être au moins égal à 100. De nos jours, nous sommes à un point où la méthode de développement de Monte Carlo sera intégrée comme outil standard dans les logiciels de SIG (Système d’Information Géographique) (Wechsler, 2007). Brown et al. (2007) ont récemment mis en place une librairie appelée DUE (Data Uncertainty Engine) pour analyser la propagation des erreurs dans une application. Aussi, une équipe à l’université d’Aston en Angleterre a-t-elle mis en place un langage informatique spécifique pour développer des programmes permettant d’évaluer l’impact des erreurs affectant les données sur les résultats d’une application (Hengl et al., 2010).

5. Discussion et conclusion

43À travers la bibliographie développée ci-dessus, nous pouvons affirmer que la création du MNT n’est pas une tâche anodine. L’utilisateur doit impérativement garder à l’esprit que tout MNT créé contient des erreurs qui vont se propager inévitablement dans les applications qui l’utilisent et peuvent biaiser considérablement les paramètres de décision qui en sont extraits. Les technologies telles que le LiDAR et la photogrammétrie sont des solutions permettant d’acquérir des données altimétriques avec une précision de quelques centimètres dans le but de générer des MNT de haute résolution spatiale. Selon l’étude menée par Petzold et al. (1999), comparé à la photogrammétrie aéroportée/héliportée, le LiDARa est bénéfique car il nécessite 20 à 30 % de budget en moins pour une même superficie. De nos jours, grâce aux avancées technologiques, l’apparition des appareils photographiques digitaux a contribué à rendre plus accessible la photogrammétrie aéroporté/héliporté par rapport au LiDARa. Une étude menée par Frastia (2005) situe le prix des caméras digitales entre 100 et quelques dizaines de milliers d’euros, tandis que le cout d’un système LiDARa (récepteur GNSS et centrale inertielle inclus) varie entre 500 000 et 1 300 000 USD (Gordon, 2011). Un tel investissement reste difficilement supportable pour des institutions publiques ou des institutions de recherches. Les systèmes LiDARa sont généralement acquis par des compagnies privées qui fournissent des services tarifés. Il est difficile de donner des chiffres car le prix dépend de la concurrence, de la densité des points, du post-traitement des données et de l’éloignement du site de mesure par rapport à l’aérodrome de décollage. En général, les fournisseurs définissent une superficie minimale pour laquelle le service demandé par le client peut être accordé. Dans les autres cas, le LiDARt et la photogrammétrie utilisant les VNP restent des alternatives accessibles, utilisables sur des zones de quelques hectares (Heritage et al., 2009a). Heritage et al. (2009a) estiment le cout d’un système LiDARt (hardware et software compris) à plus de 100 000 EUR. Cet investissement est de loin inférieur à celui du LiDARa, mais reste malgré tout élevé. En plus, il faut considérer le cout d’acquisition des batteries (500-700 EUR) pour des mesures d’une durée supérieure à 4 h. Certaines firmes proposent des possibilités de location journalière. Les prix varient légèrement d’une firme à l’autre, mais s’estiment en moyenne autour de 1 000 EUR. Cette location n’inclut pas la période de formation nécessaire afin de maitriser la manipulation du matériel, ainsi que d’éventuels traitements de données. En general, une formation de 2 à 3 jours est essentielle. Le prix des VNP peut varier de 1 000 EUR à plusieurs millions d’euros en fonction de la complexité du système (Eisenbeiss, 2009). Cependant, l’utilisation de la photogrammétrie utilisant les VNP comme méthode alternative au LiDARt n’a de sens que pour des VNP low cost. Dans la littérature, peu d’information existe sur les prix proposés par les fabricants. Des informations informelles auprès de quelques fabricants proposant des VNP à voilure fixe situent les prix entre 10 000 et 50 000 EUR, ce qui est plus abordable.

44Les résultats obtenus dans les différentes études que nous avons présentées montrent qu’il est possible de générer des MNT de haute résolution spatiale (quelques cm). L’utilisation du LiDARt reste néanmoins délicate lorsque la zone levée n’est pas nue (e.g. présence d’arbres, d’arbustes, de cultures, etc.). Cette contrainte peut être éliminée si le scanner utilisé est à écho multiple. Cela permet d’extraire l’information relative au dernier retour et donc d’obtenir les coordonnées des points au niveau du sol. En général, il faut plus d’une station pour couvrir une zone d’étude. L’obtention d’un seul nuage de point requiert que les nuages de points obtenus à partir des différentes stations soient fusionnés. Cette opération est essentielle si l’on veut éviter d’introduire des erreurs de cogénération dans les données (Coveney et al., 2011). Pour cela, un minimum de cinq cibles (de coordonnées connues) doit être commun à chaque paire de nuages de points. Heritage et al. (2009a) considèrent qu’il faut utiliser plus que cinq cibles au cas où certains sont inutilisables. De plus, les points de contrôle peuvent être utilisés pour contrôler la qualité du processus de cogénération.

45Par rapport au LiDARt, les perspectives qu’engendrent les VNP sont plus intéressantes car ceux-ci sont plus maniables (système de vols automatisés), plus rapides et moins couteux (Rose, 2012). Sa principale contrainte à l’heure actuelle reste la nécessité d’acquérir une autorisation de vol. D’autre part, l’exactitude de MNT générés à partir d’images stéréoscopiques en utilisant des algorithmes différents peut varier. Selon Hugenholtz et al. (2013), cela peut s’expliquer, d’une part, par la difficulté qu’ont certains logiciels pour corriger efficacement les distorsions créées par l’instabilité du VNP durant le vol et, d’autre part, par la difficulté de calibrer correctement les appareils photographiques.

46Des solutions couplant les avantages des VNP et de la technologie LiDARt ont été testées dans plusieurs études et semblent prometteuses (Eisenbeiss, 2009 ; Wallace et al., 2012). Le principal challenge dans cette approche est de concevoir des capteurs LiDAR miniaturisés qui ne soient pas trop lourds à embarquer pour les VNP.

47Parmi les méthodes permettant d’analyser l’impact des erreurs du MNT sur les résultats d’une application, la méthode de Monte Carlo nous semble la plus adaptée. Cependant, elle n’est pas implémentée à l’heure actuelle dans les logiciels de SIG et n’est donc pas accessible par n’importe quel utilisateur. Elle reste plutôt appliquée dans le cadre de la recherche et son utilisation demande des connaissances en programmation pour automatiser la répétabilité du processus de calculs. Comme l’a souligné Wechsler (2007), les recherches en cours permettront certainement dans un futur proche d’utiliser la méthode de Monte Carlo comme outil standard des logiciels de SIG et de pouvoir se prononcer sur la précision de tout paramètre de décision extrait d’un MNT. La méthode de Monte Carlo nous semble bien indiquée pour analyser, par exemple, l’impact des erreurs d’un MNT généré sur des surfaces agricoles en utilisant les nouvelles technologies d’acquisition des données telles que les VNP et le LiDARt.

48Liste des abréviations

49GNSS : Global Navigation Satellite System

50Lidar : Light Detection And Ranging

51MNS : Modèle Numérique de Surface

52MNT : Modèle Numérique de Terrain

53RMSE : Root Mean Square Error

54VNP : Véhicule Non Piloté

Bibliographie

Notes

To cite this article

About: Mohamar Moussa Ouédraogo

About: Aurore Degré

About: Charles Debouche