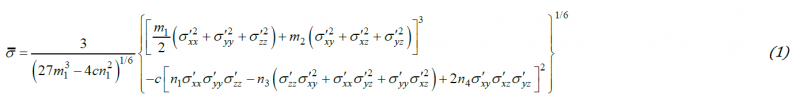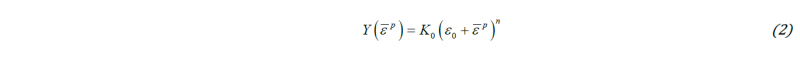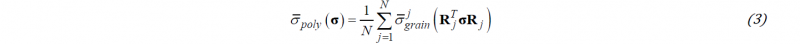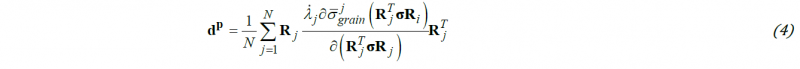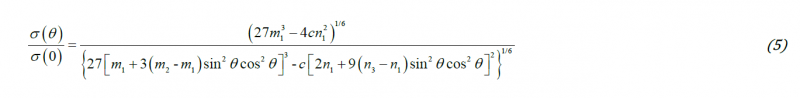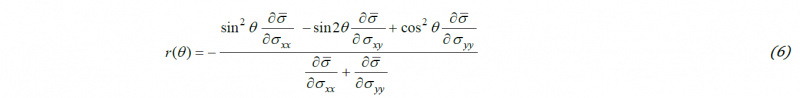1 Introduction

Since the publication of Lankford landmark paper [2] in which it was shown that the material’s initial anisotropy may have a beneficial influence on forming performance, extensive experimental and theoretical efforts have been undertaken towards development of appropriate anisotropic yield criteria. For polycrystalline metallic materials, versatile orthotropic yield criteria have been developed (for example see [3], [4]). In comparison very few yield criteria have been proposed in the literature for the description of the yielding anisotropy of single crystals (e.g. see [5]). Recently, in [1] were demonstrated the benefits of using a single crystal yield criterion that is defined for any 3-D loadings. Specifically, it was shown that this criterion involves the correct number of independent anisotropy parameters it captures the differences in yield stress anisotropy between different crystals, e.g. the differences in the anisotropy in the tensile uniaxial yield stresses with the orientation between the loading direction and the crystallographic directions (e.g. see the examples provided in [1] for aluminum and copper single crystals). Moreover, it is possible to obtain analytically the expression of the Lankford coefficient and tensile uniaxial yield stress along any crystallographic orientation (see [6]). Another advantage of using this criterion is the fact that it is C² differentiable. This in turn facilitates its implementation into finite element (FE) codes. Furthermore, using for the description of the individual grain behavior this single-crystal model, one can describe well the anisotropy of polycrystalline materials (e.g. see [7]).

In this paper, we present an application of this single crystal yield criterion to forming a cylindrical cup from a single-crystal sheet of (100) orientation. Moreover, we show that using this single-crystal model, one can describe well the effect of the spread of orientations around (100) on the anisotropy in uniaxial tensile properties.

2 Single-crystal yield criterion

The single-crystal yield criterion is defined for any stress-state. It is written in terms of cubic invariants that were deduced using rigorous theorems of representation of tensor functions. Therefore, the properties of invariance of the yield function with respect to the intrinsic symmetries associated to crystals belonging to the cubic system are automatically satisfied. Moreover, by using these representation theorems, it is ensured that the criterion involves the correct number of anisotropy coefficients such as to satisfy the crystal symmetries and the condition of yielding insensitivity to the hydrostatic pressure (for full mathematical proofs and further details, see [6] and Cazacu et al. [1]).

Let us define as Oxyz the Cartesian coordinate system associated with the crystal axes (i.e., the <100> crystal directions). In this coordinate system, the expression of the effective stress associated with the single-crystal yield criterion [1] is given by:

In Eq. (1), σ´ denotes the Cauchy stress deviator, m₁, m₂, n₁, n₃, n₄ are anisotropy coefficients while the parameter c describes the relative importance of the second-order and third-order cubic stress-invariants on yielding of the crystal. For example, all the parameters of the criterion can be determined using the experimental tensile uniaxial yield stresses in four crystallographic directions.

3 Application to forming a cup from a single crystal sheet

In the following we present the application of the single crustal yield criterion (1) to the prediction of the earing profile of a cup drawn from a single crystal sheet having the rolling (RD), transverse (TD), and normal direction (ND) of the sheet along the <100> axes of the crystal.

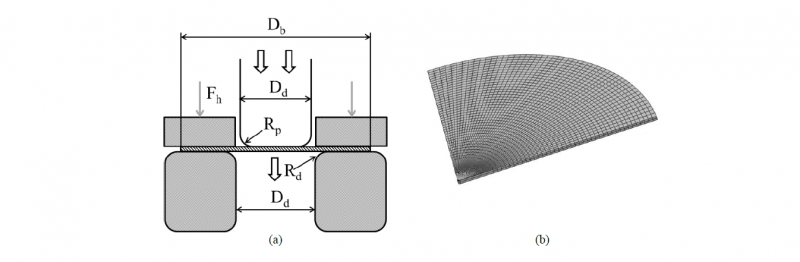
A schematic view of the cup-drawing set-up is shown in Fig. 1. The tool and blank dimensions are given in Table 1. As a result of material and geometrical symmetries of the problem, only one-quarter of the cup needs to be considered in the F.E. analysis. The blank is meshed with 4200 Abaqus C3D8H elements (8 node brick elements with constant pressure, see ABAQUS [8]). The circular blank has an initial thickness of 0.813 mm and an initial diameter of 79 mm. A blank force of 1000 N is used.

Fig. 1. (a) Schematic of the deep drawing experiment; (b) F.E. mesh for the blank.

The F.E. analysis was performed in ABAQUS/Standard using a user material subroutine (UMAT) developed by the authors for an elastic/plastic model with yielding described by the Cazacu et al. [1] single-crystal yield criterion (see Eq. (1)), associated flow rule, and a Swift-type hardening law, i.e.

where K₀, ε₀ and n are parameters, and ε̅^p is the equivalent plastic strain associated with the effective stress given by Eq. (1) using the work-equivalence principle. The numerical values considered for these parameters are K₀= 478 MPa, ε₀=0.0004 and n= 0.17. An implicit-time integration algorithm was used for the implementation of the model. In the elastic regime, the crystal was assumed isotropic, with Young’s modulus E = 69 GPa and Poisson’s ratio ν=0.3.

Table 1. Geometry of the tools for the deep drawing experiment

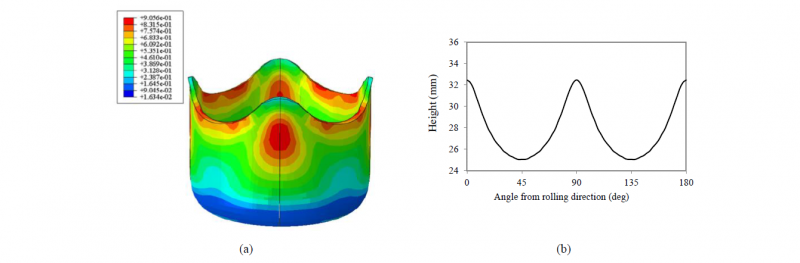
The numerical values for the anisotropy coefficients considered are: m₁=1, m₂ =0.38, n₁=0.98, n₃=0.04, n₄=0.08, c=2.3. The deformed shape of a fully drawn cup, namely the isocontours of the equivalent plastic strain are shown in Fig. 2(a). Note that the peaks in cup height are at 0° and 90° orientations (see Fig. 2(b) for the F.E. evolution of the cup height with the angle from RD ).

Fig. 2. (a) Deformed shape of a fully drawn cup of a {100}<001> single crystal sheet according to Cazacu et al. [1] single-crystal yield criterion showing the isocontours of the equivalent plastic strain; (b) Predicted cup height vs. the angle from the [100] direction (RD).

It is well known that even in the case of strongly textured polycrystalline sheets for which it can be considered that the texture has a single component, more a spread is generally observed around this component. Therefore, it is of great interest to estimate the effect of this spread on the plastic anisotropy in the uniaxial properties at the polycrystal level.

In the next section, using the single crystal yield criterion [1] for describing the plastic behavior of the constituent crystals, we describe the anisotropy in uniaxial tensile properties for sheets containing only the (100) component and being characterized by various scatter widths from this component (see Fig.3).

The effective stress of the polycrsytal, σ̅_poly(σ) corresponding to the applied stress tensor, σ, is expressed in the loading frame is considered to be of the form:

with N being the number of crystals considered in the polycrystal, σ̅_grain^j denotes the effective stress of the crystal j calculated using Eq.(1), R_j is the transformation matrix for passing from the frame associated to the crystal axes of the grain j to the loading frame. The plastic strain rate tensor of the polycrystal, d^p, is expressed in the loading frame as:

4 Influence of the spread from the ideal (100) cube texture on the evolution of the uniaxial tensile yield stress and Lankford coefficients

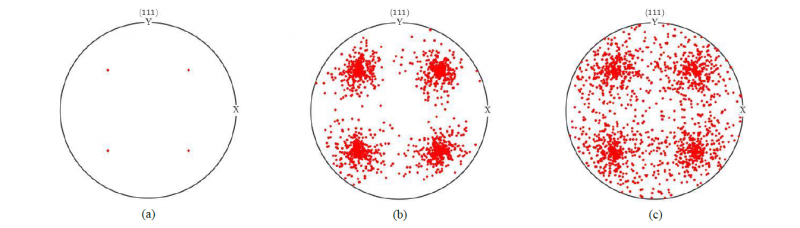
Simulations were carried out for samples of 400 crystals using the polycrystal model given by Eq. (3)-(4) for polycrystalline sheets with textures of scatter widths of 15º and 30º about the ideal (100) cube texture component (see Figure 3(b)-(c) for the (111) pole figures of the respective textures).

Fig. 3. (111) pole figure for sheets with: (a) ideal cube texture (ω₀=0°) and respectively a spread of (b) ω₀=15° (c) ω₀=30° about the ideal {100}<001> cube texture.

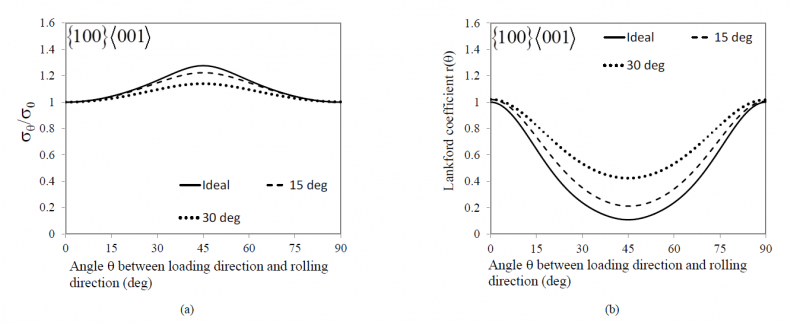
The predicted evolution of the anisotropy in uniaxial yield stresses and Lankford coefficients in the (RD, TD) plane are shown in Fig. 4.

Since in the case of a sheet with an ideal cube texture all constituent crystals have the same orientation, a single crystal yield criterion can be used. It is worth noting that with the Cazacu et al [1] yield criterion, it is possible to obtain analytically the variation of the tensile uniaxial yield stresses and Lankford coefficients with the loading direction. Indeed, for uniaxial tension in the (RD, TD) plane, with respect to the coordinate system associated with the <100> crystal axes, the only non-zero components of the stress tensor are: σ_xx=σ(θ)cos²θ, σ_xy=σ(θ)sinθcosθ, and σ_yy=σ(θ)sin²θ, with σ(θ) denoting the yield stress in a direction at an angle θ with respect to the RD direction, [100]. Further substitution in Eq. (1) leads to:

It is worth noting that the symmetry of the ideal cube-textured sheet is correctly described by the Cazacu et al. [1] single crystal model. Indeed, Eq.(6) is invariant by the transformation θ ⟶ (90°-θ), so the yield stress remains identical under rotations of π/2 about the normal to the sheet. In particular, irrespective of the values of the parameters m₁, m₂, n₁, n₃, n₄ , and c, we have σ(0°)=σ(90°) i.e. the yield stresses in uniaxial tension along the [100] and [010] directions are the same (see Fig. 4(a)). By the flow rule, the Lankford coefficient r(θ) is given by

with the effective stress σ̅ given by Eq.(1). It can be shown that irrespective of the values of the parameters of the criterion, r(θ)=r(90°-θ), and in particular, r(0°)=r(90°)=1 (for full proof, see [5]). In Fig. 4, the evolution of Lankford coefficients r(θ) and yield stress ratios σ(θ)/σ(0) with the loading direction θ for the sheets with textures given in Fig. 3, were calculated with the same set of values for the parameters describing the crystal level yielding behavior , namely m₁=1.0, m₂ =0.38, n₁=0.98, n₃=0.04, n₄=0.08, c=2.3.

Fig. 4. Numerical simulation using the polycrystal model of the anisotropy in (a) yield stress ratio σ(θ)/σ(0) and (b) Lankford coefficients r(θ) in the plane of the cube textured polycrystalline sheets. The textures for different scatter width are shown in Fig.3. The results for the ideal texture ω₀=0 were obtained with the analytical formulas (Eq.(5)-Eq.(6)), respectively.

Note that even for the ideal cube texture both the predicted yield stresses and Lankford coefficients vary smoothly with the loading orientation (Fig.4), for the values of the parameters considered, there are extrema only at 0º , 45º, and 90º to the [100] direction in the (100) plane. It is worth recalling that for an ideal cube texture, the yield stress variation with the loading orientation according to the Taylor-Bishop-Hill model displays two cusps and infinite values are predicted for the Lankford coefficients along the 0º (i.e. RD) and 90º (i.e. TD) tensile loadings (see [9]). Additionally, the TBH model predicts a smooth variation only if the texture is characterized by a very large spread (see simulation results presented in [9]).

5 Conclusions

The capabilities of the single-crystal yield criterion recently developed by Cazacu et al [1] was illustrated. It was shown that using this single crystal yield criterion, the Lankford coefficients exist and have finite values for all loading orientations. Moreover, the variation of both the yield stress and Lankford coefficients with the crystallographic direction can be expressed analytically. Furthermore, it was shown that using Cazacu et al.[1] single-crystal model to describe the anisotropy of individual constituent crystals, the effect of texture on the Lankford coefficients and yield stresses of a polycrystalline sheet can be reasonably described. With regards to deep drawing simulation, according to Cazacu et al [1] single-crystal model, the number and location of the extrema in the height of the drawn cup is dictated by the crystal orientation, for e.g. a minimum of four ears for the (100) crystal orientation. Whether at the respective locations, the criterion predicts minima or peaks for the height of the cup depends on the parametrization used for the criterion. For the parameterization considered in this papers, peaks are at 0º and 90º. The same general conclusion concerning the influence of the parameterization on the earing predictions also holds true for all the yield criteria for polycrystalline materials (e.g. Hill 1948 [10], Yld 91 [11], Yld 2004-18p [12], BBC 2010 [13], Cazacu et al. [14], etc.) as has been clearly demonstrated over the years in the literature and Numisheet benchmarks.

Acknowledgements

Partial support for this work provided by the AFOSR grant # FA9550-18-1-0517 is gratefully acknowledged.