1 Introduction

Due to climate change, car manufacturers are more and more demanding for weight reduction where steel or aluminum products cannot answer anymore. Materials with lower density, like fibers reinforced plastic shows interesting specific strength and stiffness that could help to decrease the weight while still satisfying the requirements. On the other end, lightweight materials and their related manufacturing processes with long cycle times are mostly more expensive which could lead to higher costs. This is a clear limitation in the use of composite materials in the automotive industry, especially when the replacement from the metal part is a 1:1 replacement keeping the same functionalities. One way to overcome that cost barrier is to combine or even add extra functionalities to the part that is targeted to be lighter.

In a vehicle suspension, the anti-roll bar (ARB) reduces the amount of body roll during cornering. This stiffening coupling between both sides of the vehicle enhances handling but deteriorates passengers’ comfort. This work aims to design a new composite design for the ARB. In addition to the drastic decrease of weight, a progressive stiffness behavior with deformation could be expected using the anisotropic nature of composite. The progressive behavior will improve the compromise between comfort and handling, keeping low stiffness at low roll angle around the equilibrium combined with a higher stiffness for higher roll angles.

2 Design and engineering simulation

2.1 Component functionality and design

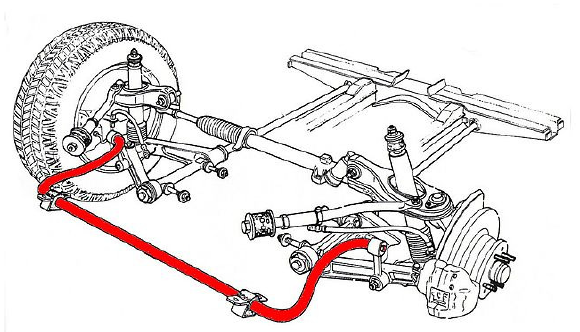
In a suspension system, the anti-roll bar (ARB), also known as torsion bar, sway bar or stabilizer, is an optional vehicle component that connects both wheels on a vehicle axle. It influences on driving comfort and handling (i.e. cornering behavior, rolling motion and stability) of the car as well as on driving safety and traction. It is made out of a solid or hollow bar with a threedimensional shape. It can be used in front suspension, rear suspension or in both suspensions, independently of the type of suspension [1]. Fig. 1 schematically shows the component and its position in a passenger car.

Fig. 1. Anti-roll bar (ARB) (in red) and its position in a vehicle suspension system [2].

When one wheel on the vehicle axle moves up or down relative to the other wheel, the central section of the ARB undergoes a torsion load. The arms at the end of the component undergo a bending load and transfer the linear wheel motion into a torsion of the central section. The stiffness of the component can be expressed by looking at the vertical wheel motion and corresponding forces at the wheel, or by looking at the angular moment and angular deformation of the central section of the .

The sporty character of the vehicle depends on the ARB’s stiffness at high roll angle (high stiffness results in better cornering handling), while the comfortable character of the vehicle depends on the ARB’s stiffness at low roll angle (less stiffness means more comfort). This is a compromise which is hard to solve with a fixed stiffness linked to design and material. Typically for the low-end vehicle segment an ARB could be not present at all or, if it is present, it is made in steel. In any case, this results in an equal stiffness for low and high roll angles. The high-end vehicle alternative is an active suspension system based on active dampers. An interesting alternative would be to have a progressive stiffness behavior coming from the material properties; i.e. low stiffness at small angles for comfort, and higher stiffness at high angles for handling. This is illustrated in Fig. 2.

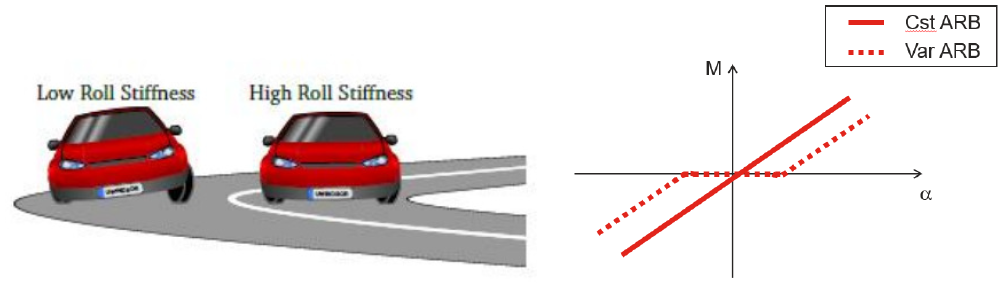Fig. 2. Low and high roll stiffness (right) [1] and progressive stiffness with torsion to improve comfort around the center point (left), allowing a compromise between comfort and handling.

In this specific study, the ARB on the front axle of an Audi A6 acts as the reference component, shown in Fig. 3. It consists of a hollow steel bar (diameter 27.25 mm and wall thickness 3,15 mm) with a weight of 2.85 kg. Seen from the front of the vehicle, the component’s width is approximately 1075 mm. The peak wheel load is 1705 N. The moment arm of the acting load around the axis of the central section is approximately 150 mm, resulting in a maximum torque of 255 Nm on the central section of this ARB.

Fig. 3. Front ARB of an Audi A6.

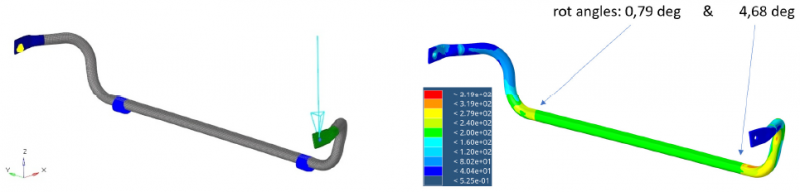
The reference component was 3D scanned to obtain a CAD representation and subsequently, a finite element (FE) model was set up. The FE model consists of 2D shell elements and a linear static load case. One end of the ARB is clamped, while a load of 1705 N is applied on the other end. Under this load, the central section rotates approximately 3.9 degrees. Fig. 4 shows the FE model and the calculated results. This corresponds to an angular stiffness of 65 Nm/deg, which is subsequently used as the design point at maximum load. To obtain a progressive stiffness, this value needs to be lower at lower loads.

Fig. 4. FE model of the reference ARB, model setup (left) and calculated results (right – stresses as color and deformations annotated)

2.2 Composite unit cell simulation

In a preliminary study to determine of the material mechanical properties, the complex structure of a braid can be locally simplified with a unidirectional (UD) laminate, neglecting any effect from the yarn crimps [3]. The two yarns of a biaxial braid can be seen as UD plies with a fiber orientation of +θ and – θ, where θ is the braiding angle, as illustrated in Fig. 5(a). This approach was used in [4] for the calculation of the stiffness constant of a carbon fiber automotive ARB, reporting a 7% difference with the experimental values measured in the prototypes. The Altair ESACompTM® software [5], which applies the classical laminate theory (CLT) [6], is used to calculate the mechanical properties of this UD laminate starting from the engineering constants of the selected fibers (S-glass) and matrix (epoxy) as reported in Table 1.

Table 1. Average properties for the selected fibers (S-glass) and matrix (epoxy).

A more punctual description of the braid structure is achieved using WiseTex [7], a software package developed in K.U. Leuven, for the modelling of composite textile structures. WiseTex is able to consider the real path of a yarn in the unit cell, modelling the effect of crimp and providing an improved description of the internal geometry [8]. A graphic representation of the braid structure modelled in WiseTex for θ= 45° is reported in Fig. 5(b). The S-glass fibers tows are modelled as elliptical with d1=0.28 mm and d2=1.25mm, with the same mechanical properties shown in Table 1. The fiber volume fraction estimated in WiseTex, Vf ≃ 72%, was used also for the UD plies created in ESAComp^TM.

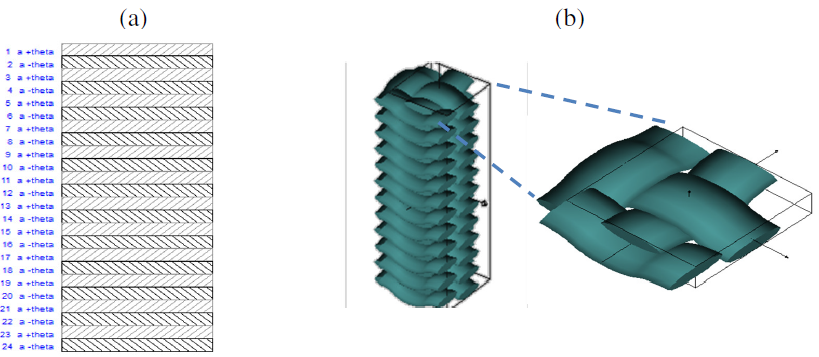Fig. 5. (a) UD model in ESACompTM and (b) braided structure model in WiseTex.

The two different modelling approaches of the local composite structure are specifically used to calculate the dependency of the material engineering properties from the braiding angle in order to select the appropriate one to maximize the stiffness to weight ratio of the final component. The calculated results for longitudinal and transversal modulus with respect to the braiding direction E_XX, E_YY and G_XY are compared in Fig. 6.

The Young moduli E shows the same dependency from θ in both models, but the braided structure model of WiseTex forecast a modulus up to 30% higher. On the other hand, the modulus of shear G, crucial for the torsional properties of the bar, present a relative minimum at θ=45°, and two maxima at 25° and 65° in the braided model, in contrast to the bell shape curve centered at 45° calculated with the UD model. A similar trend was reported in [8] for a WiseTex simulation on a sheared woven structure and experimentally, but with very scattered results, in [9] for a braided glass fiber composite.

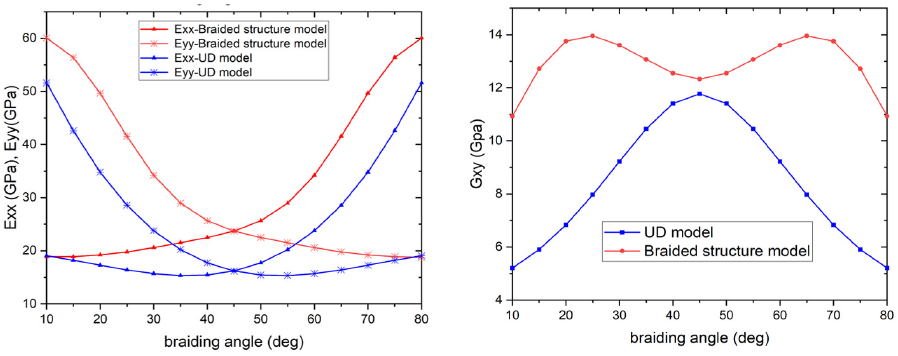Fig. 6. (left) predicted elastic moduli from the UD model (blue) and braided structure model (red): the left graph shows the longitudinal and transversal modulus w.r.t. the braiding direction (Eyy and Exx, respectively), while the right graph shows the in-plane shear modulus.

2.3 Multi-scale simulation

The finite element analysis (FEA) of composite structure started by generating a material model using Altair Multiscale Designer^TM. First, the Unit Cell Model was defined. The best accuracy of the model is possible by selecting a fibrous parametric model with honeycomb configuration. The control variable is the fiber volume fraction amount V_f=55 %. An FEA unit cell model is shown in Fig. 7.

Fig. 7. Unit cell model of S2-glass fibers 463-AA-675 4059 with epoxy matrix.

In the next step, linear material characterization, the micro material properties of the model (matrix and fibers) were defined for forward homogenization. From constituent material database, epoxy (Std. Modulus) and S-2 glass fibers 463-AA-675 4059, both with isotropic symmetry type has been chosen. Furthermore, two lay ups were homogenized, to obtain material properties across the fiber and shear properties (see Table 2).

The final step in material model development is nonlinear material characterization. Based on ply layups from linear material characterization for the phase one (matrix) an orthotropic damage and RI Plasticity damage law was calculated. For phase two (S2 glass fibre) an isotropic damage – bilinear damage law was used. The simulation model for macro simulation was based on 3 Unit Cell Model simulation tests, namely two tests for layup 1: tensile test (0 degree along the fibers) and tension test (90 degree across the fibers) with duration of 1 s, max strain of 0.05. The third test was shear test of layup 2 (+-45 degree). Simulation results are presented in Fig. 8.

Table 2. Constitute and Homogenized material properties for FEA.

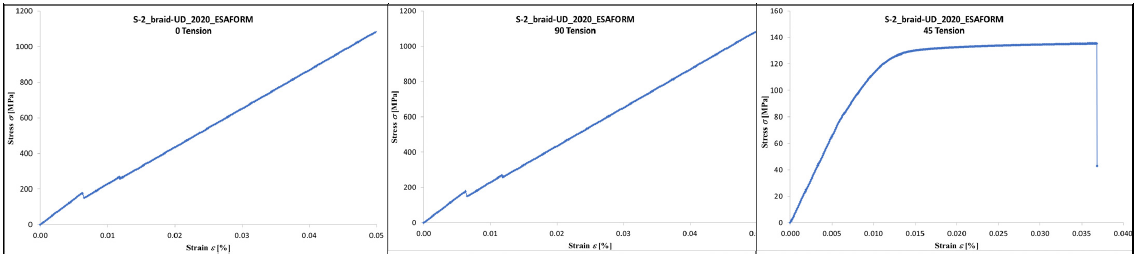Fig. 8. Test curves obtained from nonlinear material characterization using tensile testing in 0° (left), 90° ( middle) and 45° (right).

These test results were exported as material data file (material card) for implicit simulation of the ARB. In Altair OptiStructTM a layered model of composite ARB was built. The model consists of 16 plies, defined as continuum shell elements (PCOMPLS property card) with thickness of 0.279 mm and reinforcing and stacking sequence [45,-45]₈. This element type was applied to capture through thickness deformation of the structure. After applying of boundary conditions and loads (see Fig. 9) the large displacement, non-linear static analysis of ARB was run.

Fig. 9. Lamina of ARB with load applied at RBE3.

Looking at layered solid composite stresses for P1(major) Stress (solid), as shown in Fig. 10(left), the main stress occurs at transition zone between the smallest diameter of 27 mm and conical connecting tube part. The stress here is about 63.38 Mpa respectively to σ_Failure=1085.90 MPa at failure strain of ϵ=5 %.

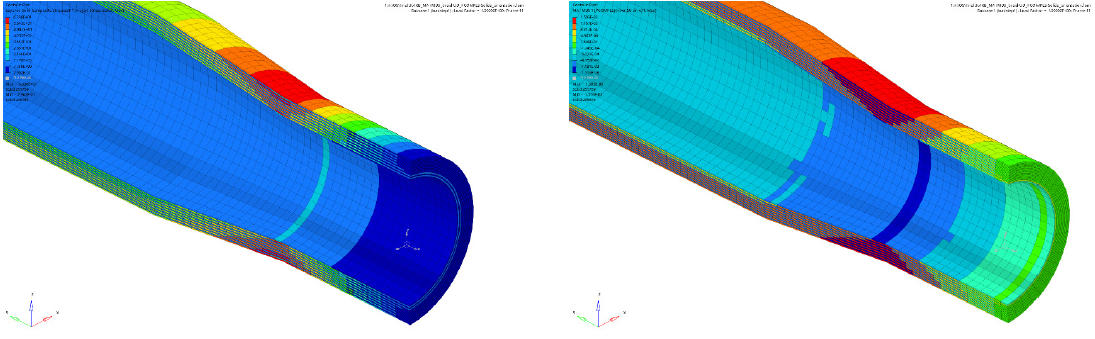Fig. 10. (left) Layered Solid Composite Stresses in transition area P1 (major) Stress (solid) along the fiber in 45°direction.

(right) Fiber Strain e11

Looking at Homogenized Strain e11 in fiber direction with max value of 0.0015 (0.15 %) is by far not critical, the material failure strain in fiber direction being about e=5 % (Fig. 10(right)). The same is for Homogenized Strain transverse to fiber e₂₂ reaching 0.0014 (0.14 %). Other strain components (e₃₃, e₂₃, e₁₃, e₁₂) are small too. The Homogenized Eigenstrain values approve no plastic or incrementable strains in the ARB. Matrix Equivalent Volumetric strain with max value of 0.00035 (0.035 %) confirm the absence of brittle failure. Finally, Fiber Strain Values shows cohesion with homogenized values.

3 Prototype production

Production of demonstrators took place at Institut für Textiltechnik at RWTH Aachen University. In the first step the mold for wax core casting is derived from the ARB geometry shown in Fig. 11. The mold from Ureol SikaBlock® M600, is reworked using 5 axis milling machine (Maka MK 7 s). For casting, a stearin paraffin mixture is used.

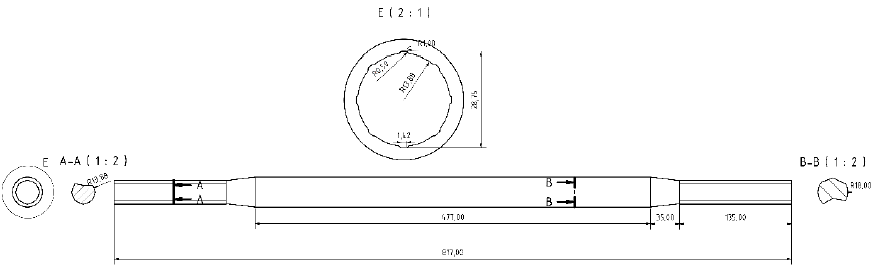Fig. 11 Composite ARB design

After wax core casting the overbraiding is performed. Using radial braiding machine, Herzog RF 1-64/120, 64 rovings are braided to a 1:1 braid pattern on the wax core. For that S-2 glass fibers 463-AA-675 4059 from AGY AIKEN, LLC, USA is used.

Table 3. Samples overview.

The resin infusion is conducted in Vacuum Assisted Process (VAP^®) using vacuum injection. The overbraided ARB samples are overwrapped with peel ply fabric and layer of perforated foil. Together with infusion mesh the setup is placed in membrane which is permeable to gas but impermeable to resin. That setup is finally placed in a vacuum bag to support air removal and to apply necessary pressure. For infusion, epoxy resin from HEXION EPIKOTE™ Resin MGS™ RIMR426 with curing agent EPIKURE™ Curing Agent MGS™ RIMH435 is used. After curing of the ARB samples are placed in the oven for thermal treatment of the matrix. During that process, the wax is also removed from the part. Finally, the ends of the ARB are cut to designed length using a multi-tool.

4 Validation testing

4.1 Test set-up

As explained in the previous sections, the central section of the ARB should provide the progressive stiffness functionality. Consequently, a setup for testing the rotational stiffness of the central section has been conceived.

Fig. 12(top) shows the test setup: one side of the setup is fixed to the ground, while the other side connects to a hydraulic rotational actuator (IST PD1F) with a maximum torque of 1000 Nm. The torque is measured by a torque transducer (type GTM MF) with a range of 1000 Nm and an accuracy of 0.5 Nm. The angle is measured by a rotational transducer (type Burster 88603- 001) with a range of 60°, an accuracy of 0.03° and a resolution of 0.01°. The central section of an ARB sample is subjected to the torque load by using a pin on both ends. A static test is executed by applying a torque load of 250 Nm at a rate of 30 Nm/s.

Fig. 12. (top) Test set-up with an original steel sample; (bottom) a glass fibre composite sample

At the moment of writing, four samples (central sections) have been tested: an original steel sample (see Fig. 12(top)) and 3 glass fibre (GF) composite samples of the configuration 45x4, 45x6 and 30x6 (cf. Table 3). An example of a composite sample is shown in Fig. 12(bottom). Putting a pin directly through the GF tube would tear the material apart. Therefore, steel adapters are glued into the GF tube. This connection is similar to how the GF central section would be attached to the ends of an ARB in order to fit into a vehicle suspension. The adhesive connection consists of an Araldite 2011 2C-epoxy adhesive with a thickness of approx. 0.1 mm and an overlap length of 35 mm. The steel part was sandblasted to a roughness Ra of approx. 4μm. The inside of the GF tubes were sanded and plasma treated (500 kW at 20 mm distance). Curing of the adhesive was performed at 23°C for 24h followed by 80°C for 30 minutes.

4.2 Test results and analysis

Fig. 13 shows the torque-angle curve for two tested samples. The steel sample reaches 250 Nm and has a stiffness of 55 Nm/°. The composite 45x4 sample only reaches 100 Nm. At that torque, the adhesive fails. The torque-angle curve up to that point shows a linear behaviour and a stiffness of 16 Nm/°.

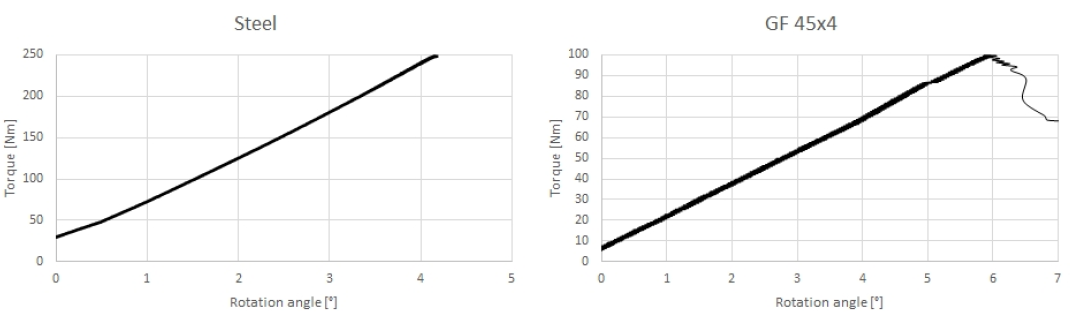Fig. 13 Torque-angle measurement result for (left) steel and (right) glass fibre composite sample (configuration 45x4)

Enhancements to the adhesive connection (e.g. adding longitudinal grooves in the steel adapters) will improve the load carrying capacity of the adhesive connection. The stiffness of the composite section will need to be increased by adding more layers. Increasing the outer diameter is not an option due to packaging restrictions on the underside of the vehicle. In this sample, no progressive stiffness is observed, yet the adhesion failure at a torque much lower than the operating torque of 250Nm makes any conclusion on this premature. No statement can be made yet about the strength of the composite sample.

The left-hand side of Fig. 14 shows the torque-angle simulation results in comparison to the steel reference test. It can be seen that a GF 45x8 sample (consisting of 8 layers) would exhibit a stiffness similar to the original steel ARB. The right-hand side of Fig. 14 reports the resulting overall stiffness value for simulations and all tests conducted so far. Overall, the stiffness obtained in the tests increases with the number of layers, yet the stiffness values are significantly lower than the corresponding simulation results. There is also no substantial difference in stiffness measured between the samples with 30° and 45° braiding angle.

Fig. 14. Comparison between test results (test-orig: steel ARB; test-45x4: composite ARB with 4 layers) and simulation results with 4 and 8 layers.

5 Conclusions

This paper presents the methodology and initial results on the design, simulation and functional testing of a composite anti-roll bar with progressive stiffness by braided glass fibre composite. Extensive Unit Cell Finite Element (FE) simulations have indicated that torsional stiffness may be significantly higher (up to 20%) for braiding angles that deviate from 45°, however this is not confirmed with initial test results of just two samples. The in-depth Multi-Scale FE simulations indicate that typical glass fibre limit strains do not pose an issue for the foreseen application. On the other hand, the first torsional test results point out the significance of the connection strength between the composite central section and the steel arms of the ARB, which is apparently insufficient for the initial test samples. Further testing with samples of increased connection strength may scrutinize further the functional behaviour up to the design load including progressive stiffness, as well as the stiffness dependency on the braiding angle.

Acknowledgements

This research was partially supported by Flanders Make, the strategic research centre for the manufacturing industry. This paper is realized in the Light Vehicle project (https://www.lightvehicle2025.eu/), which is funded by Interreg Euregio Meuse-Rhine and supported by the European Regional Development Fund. The Interreg V-A Euregio Meuse-Rhine (EMR) programme invests almost EUR 100 million in the development of the Interreg-region until 2020. This area stretches out from Leuven in the west to the borders of Cologne in the east, and runs from Eindhoven in the north all the way down to the border of Luxemburg. Over 5.5 million people live in this cross-border region, where the best of three countries merges into a truly European culture. With the investment of EU funds in Interreg projects, the European Union directly invests in the economic development, innovation, territorial development and social inclusion and education of this region.