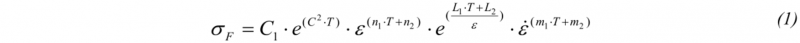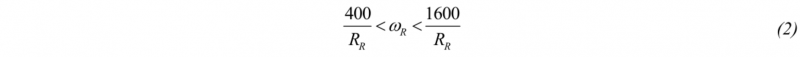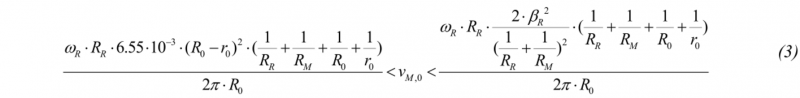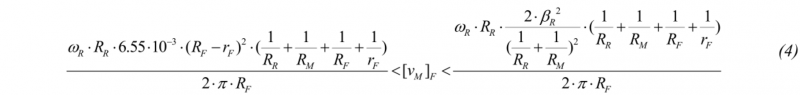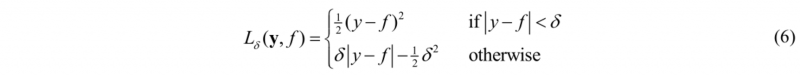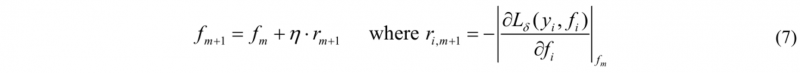1 Introduction

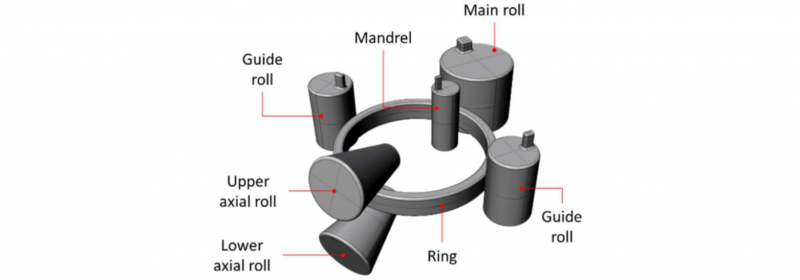
Radial axial ring rolling (RARR) is an incremental forming process in which an annular blank is deformed radially by the movement of the mandrel and the main roll and vertically by the two axial rolls, for obtaining a final ring. Besides, for better control of the process, two guide rolls are displaced as shown (Fig. 1).

This industrial process guarantees a wide range of products that find usage in different sectors including aerospace, agricultural, automotive, piping, and wind power [1]: the versatility of this process has driven forward the research to analyze this productive system. These investigations aim to better understand the ring rolling system, including the influence of process parameters and ring evolution, force distribution, and dynamic behaviors. Over the years, the numerical simulation of this complex process has taken over on experimental analysis, thanks to the growing developments of computational performance: advantages in terms of time and costs are so obtained [2]. Even if the finite element (FE) analysis have reduced the response time [3], they still required much computational time in a growing specific process that demand for on-time solution and optimizations. Predictive approaches based on mathematical models can be a valid answer: compared to the numerical model, they do not require any specific knowledge to be used. Several studies have been conducted to provide a reliable predictive model for the ring rolling process.

Considering the process design, it has been proven that the process parameters influence the temperature distribution on rings and rolls [4] and they affect the mechanical proprieties of the ring [5]. In Guo and Yang [6] paper, a mathematical model has been found, based on constant speed growth condition of ring and a steady forming condition has been defined in order to improve the stability of the process and its design. Gheisari et al. [7] conducted a 3D-FE analysis in hot forming conditions, obtaining an optimization guide of process parameters and quality control. Seitz et al. [8] investigated the ring rolling process for realizing seamless composite rings to maximize the mechanical properties. Considering the optimization of final quality, Anjami et al. [9] have demonstrated that tool size influences strain and temperature distribution, finding the optimal configuration and reducing the fishtail effect.

Fig. 1. Configuration of the ring rolling process [6,8,12].

Concerning the RARR process forces estimation, several authors [10] have implemented models for roll forces prediction in good agreements with experimental results and with errors lower than 17 % for axial roll and 12 % for mandrel [11]. Quagliato and Berti [12] considered different analytical models for calculating the radial and axial forming forces and they compared the results with FE simulation obtaining good results. Johnson et al. [13] experimentally validated that roll force decreases importantly when the contact area between tools and ring decrease by 2/3 from the initial contact zone. Forouzan et al. [14] proposed a new FE simulation method that improves the computation time and gives more detailed results on tool-ring interface and roll force. Quagliato et al. [15] used the slip line theory to develop a mathematical model that predicts process forces with a maximum error of 10 %. Later, Quagliato et al. [16] proposed a new algorithm based on slip line theory to provide radial and axial forces with a maximum error of respectively 5 % and 6 %: this model is valid for any bulk deformation process with curved geometrical contact between workpiece and tool. The increasing market requirements and attention on energy saving in all industrial processes demand deeper research on energy consumption optimization. Giorleo et al. [17] focused on the initial process phases and analyzed their influence on forces and energy consumption. Liang et al. [18] studied titanium alloys ring rolling processes using FE models analyzing local defects due to low thermal conductivity and concentration of forming energy. Larkiola et al. [19] developed an artificial neural network model to study the energy efficiency of the rolling process starting from given product geometry and mill settings, obtaining an improvement of 1.8 % in terms of efficiency.

The research purpose is to add a further element to RARR energy analysis, comparing a multi-variable regression model and a Gradient Boosting model. Several process variables are involved in developing the two models and three different materials are considered. To create the necessary set of data and developing the predictive models, 380 FE simulations have been implemented in a commercial software: the process parameters have been calculated with the algorithm proposed in Berti et al [20] developed via an analytical process. The multivariable regression model results more inefficient in terms of practicality with an equation of 26 parameters: the Gradient Boosting approach turns out to be more reliable for energy consumption estimation for the RARR process. The developed FE model, utilized for the definition of the training database for both the regression model as well as the GB model has been validated against previously published results, showing a maximum error equal to 2.15 % in the prediction of the radial forming force, utilized for the estimation of the mandrel force impulse integral, used as a reference for the energy consumption during the process.

2 Finite element model implementation

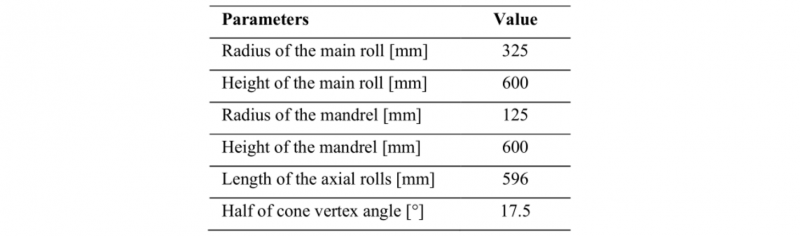
To create a database for the implementation of the models, numerical simulations have been carried out utilizing commercial software called Simufact.Forming 15 utilizing the process schematic of Fig. 1. The dimensions of the tools are summarized in Table 1 and are considered as rigid with heath transfer. The initial temperature of the tools is 150 °C, while the environment is set to 50 °.

Friction has been modeled utilizing the constant shear friction model set to m = 0.85 for the contact between ring, mandrel, and main roll and to m = 0.6 for the contact between ring, axial rolls, and centering rolls. The ring geometry is meshed utilizing a ringmesh algorithm with hexahedral elements and the sizes in the three dimensions are 20 mm (axial), 18 mm (radial), and 20 mm (tangential). The solver chosen is based on a direct approach, called MUMPS Parallel Direct, and gives accurate results for large dimensions matrixes while also granting a good compromise with the computational time [15,16].

Table 1. Tools dimensions.

Concerning rings, the materials used for each combination of simulations are: i) 42CrMo4 steel, ii) Inconel 718 super alloy and iii) AA6082 (AlMgSi) aluminum alloy, largely utilized for the manufacturing of rings by means of ring rolling process under hot forming conditions [1]. The properties of these materials are taken from MATILDA® (Material Information Link and Database Service) archive, available in the Simufact.Forming 15 database. The flow stress (σ_F) approach utilized is based on equation (1) derived from the Hansel-Spittel model [21].

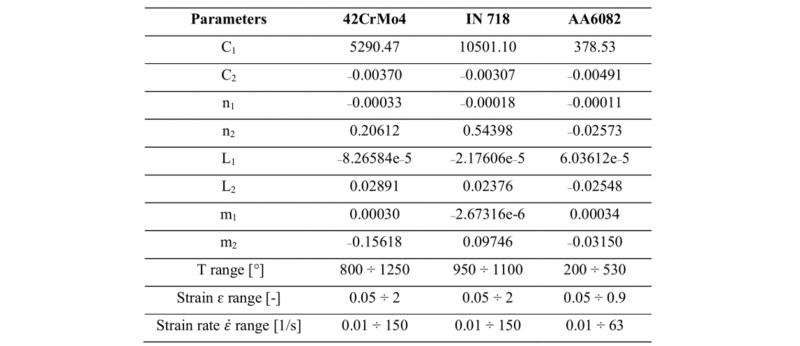
The relevant constant, for the three considered materials, are reported in Table 2.

Table 2. Validity range and Hansel-Spittel flow stress model constants for the three considered materials.

In order to consider the influence of the materials and the chosen process parameters in the energy prediction models, different combinations of materials, temperature, process-dependent properties (Table 3), and process parameters, as hereafter summarized, have been considered in the FE model development.

Table 3. Temperature, Young’s moduli, and Yield strengths for the three considered materials.

he process parameters utilized for the developed models and set on the FE analysis are: i) main roll rotational speed, ii) initial feeding mandrel speed and iii) final feeding mandrel speed. The equations for the calculation of these parameters are reported in Eq. (2), Eq. (3), and Eq. (4) and detailed in Berti et al. [20]. These equations are based on the slip-line theory and assume no slippage between the main roll and ring. In Eqs. (2) - (4), ω_R is the rotational speed of the main roll, R_R the main roll radius, R_M the radius of the mandrel, R₀ and r₀ the outer and inner radius of the ring preform, R_F and r_F the final outer and inner radius of the ring upper wall, ν_M,0 and , ν_M,F the initial and final mandrel feeding speeds whereas β_R is the friction angle.

A total of 380 simulations have been implemented considering 16 initial/final geometry sets where the considered ring final outer diameters are 650, 800, 1100, 1400, 1700, and 2000 mm and where the above mentioned material, ring initial temperature, and process parameters have been changed to account for their influence on the energy consumption during the process.

3 Energy prediction models definition

In this paper, a multivariable regression model and a machine learning-based algorithm are considered and utilized for the prediction of the energy consumption in the RARR process. For the model training 315 out of the 380 FE simulation results have been utilized whereas the remaining 65 cases, randomly selected, have been utilized for validation purposes.

The differentiation between training and test databases allows investigating the accuracy of both models when asked to predict the energy consumption, defined as the force impulse over mandrel feeding time, for the case of data sets not included in the training database but still belonging to the same variable intervals.

3.1 Multi-variable regression model

Multivariable regression models are well suited for determining the dependence between a dependent variable and independent variables. In this research, the regression model is build using Minitab 17 software and the fit-regression model is used for describing the connection between the variables of the ring rolling process and energy consumption. The interaction and polynomial terms are included considering a second-order multiple-linear regression Eq. (5) where b₁ , b₂ are the linear effect parameters, b₁₁ , b₂₂ are the quadratic effect parameters and b₁₂ is defined as interaction effect parameters.

The model constants are calculated by the least-squares method whose main purpose is to reduce the sum of the deviation of the regression line. For obtaining a good set of parameters on the final model, a stepwise process is used [22]. For optimizing the stepwise result, several tests with different values of alpha-to-enter and alpha-to-remove have been considered, allowing to conclude that the value of 0.5 for both alpha-to-enter and alpha-to-remove gives the best result in terms of residuals.

3.2 Gradient Boosting model

Gradient Boosting is a machine learning technique that progressively updates the objective function L_δ(y,f) intending to minimize the difference between predicted ( f ) and true ( y ) values [23]. In Eq. (6), δ is defined as a hyperparameter and it is optimized to 0.9 during the progressive training of the algorithm through several attempts.

The update of the predicted value is based on the accuracy of the previous step and on the learning rate ( η ), which slows and accelerates the update of the learning process according to the current and previous performances to define the right path for the minimization of the residuals.

4 Experimental and literature validation

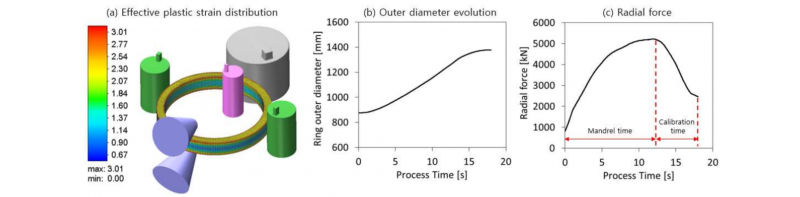
For the definition of the database for the training of both the regression and the GB models, 380 thermo-mechanical FE simulations have been implemented considering the conditions listed in section 2. For a matter of conciseness, the details concerning all the study cases cannot be included in the paper but are available on request to the corresponding author. An example of the final shape of a 1400 mm final outer diameter ring realized with Inconel 718 superalloy and with an initial temperature equal to 1070 °C is reported in Fig. 2a, for the effective plastic strain distribution at the end of the forging, and in Fig. 2b and 2c, for the prediction of the outer diameter and radial forming force evolutions during the process.

Fig. 2. (a) Effective plastic strain distribution and (b) outer diameter evolution for a R_F=1400 mm, (c) T₀=1070 °C ring made of Inconel 718 superalloy.

In the research presented in this paper, the energy is estimated as an impulse through the radial forming force integral over time. As shown in Fig. 2c, the mandrel time, defined as the time during which the mandrel is acting towards the ring inner diameter, differs from the total time, which also includes the calibration time. Since the calibration time is normally a user-defined parameter, it has not been included in the calculation of the force impulse integral.

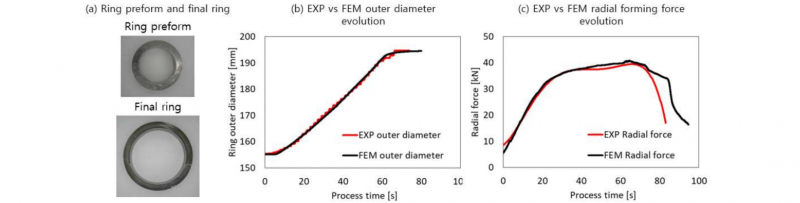
For the validation of the proposed thermo-mechanical 3D FE model, the experimental results previously presented in [16] have been considered and are relevant for a Pb75-Sn25 alloy preform ring manufactured under cold forging conditions. The initial dimensions for the ring preform are D₀=155 mm (outer diameter), d₀=105 mm (inner diameter), and h₀=42 mm (height) whereas the final dimensions are D_F=195 mm (outer diameter), d_F=153 mm (inner diameter), and h_F=37 mm (height), as shown in Fig. 3a. As shown in Fig. 3b and 3c, the implemented FE model is able to catch both the geometrical evolution of the ring throughout the process as well as to properly estimate the evolution of the radial forming force, the key-parameter for the correct calculation of the force impulse integral. The maximum error in the estimation of the outer diameter and radial forming force evolution during the process is estimated in 0.95 % for the former and 2.15 % for the latter, respectively.

Fig. 3. (a) Ring preform and final ring, comparison between FE analysis and experimental results for the (b) ring outer diameter and (c) radial force.

Employing the implemented and validated FE model, the above-mentioned 380 numerical simulations database has been constructed by exporting the radial forming force and the mandrel time and calculating the force impulse integral. Therefore, for both the regression model as well as the GB model, the energy target function (dependent variable) is defined as the force impulse whereas the influencing parameters (independent variables) as the above-mentioned, material, process settings, and boundary conditions. Among the 380 simulations, 315 have been randomly selected for the training of the models whereas the remaining 65 for its validation.

5 Results

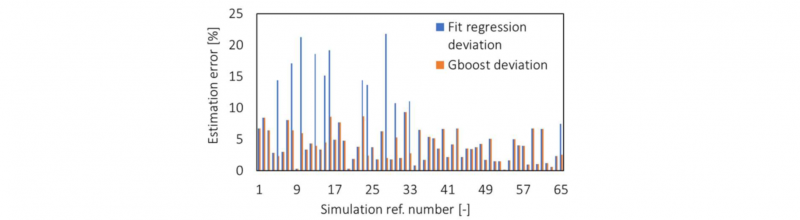
As concerns the regression analysis, implemented in Minitab 17, the resulting equation is composed of 26 parameters and the maximum and average deviations between predicted and measured results are estimated in 21.8 % and 5.9 %. However, the complexity of the equation and the relatively high maximum error make this approach to be impractical for industrial application. For this reason, a machine learning approach based on the Gradient Boosting method has been utilized and implemented in a Windows-10 OS environment by means of a Python 3.7.4 script [24] with Spider 4.2.1 program. Also, for the case of the GB model, the same dataset for training and validation has been utilized. The percentage deviation between measured and predicted values for the force integral over time, for the two considered methods, are reported in Fig. 4.

Fig. 4. Percentage deviation between measured (FE) and predicted force impulse results for the Fit-regression model and Gradient Boosting model.

For the case of the GB approach, the maximum and average deviations in comparison to the measured results are estimated in 9.3 % and 3.9 %, proving an improvement in comparison to the fit-regression model, especially in terms of the maximum error. In addition to that, the GB program is more compact, and, being Python 3.7.4 an open-source language, it can be applied to different databases without the need for a specific program, like Minitab 17. The developed Python 3.7.4 script for the GB algorithm is available on request to the corresponding author of this paper.

6 Conclusions

In this study, two performances of a multi-variable regression algorithm and a machine learning-based approach for the prediction of the energy consumption in the radial-axial ring rolling process are presented. The numerical simulation model, utilized for the definition of the training and validation databases, has been validated against previously published results and showed good accuracy in both the prediction of the geometrical expansion of the ring as well as in the estimation of the radial forming force, utilized for the calculation of the energy impulse over the mandrel feeding time.

As concerns the two investigated algorithms, the Gradient Boosting approach has shown to be better suited for the estimation of the energy consumption during the process thanks to its higher accuracy and quick implementation on open-source programs. Moreover, the proposed approach can also be extended to different forging process allowing to quickly and precisely estimate the energy consumption without the need for high time-consuming 3D thermo-mechanical simulations and, finally, it is aimed to be further improved in order to define the best combination of process parameters and boundary conditions those allow to minimize the required force for the manufacturing of a specific ring geometry combined with a selected material.

Acknowledgments

This work was supported by the Material Component Technology Development Program (20013060) funded By the Ministry of Trade, Industry & Energy (MOTIE, Korea) and by the National Research Foundation of Korea (NRF) grant funded by Korea government (MSIT) (No.2019R1F1A1060567). Moreover, this research was results of a study on the “HPC Support” Project, supported by ‘Ministry of Science and ICT’ and NIPA.