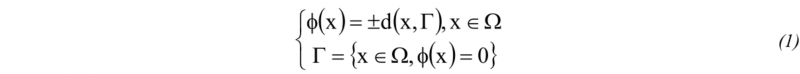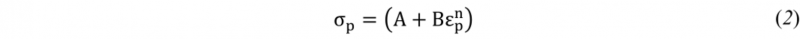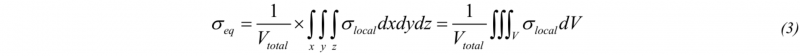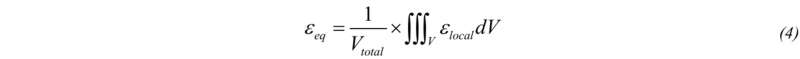1 Introduction
Foamed polymer materials are widely used in automotive, aeronautic and packaging industries due to their low density, strong ability to absorb impact loading, and their good thermal /acoustic properties. The final properties of such material depend strongly on the process that will induce specific microstructure characterized by volume fraction of pores, pores size/shape distribution, and neighbor distance distribution between pores. The purpose of this study is to generate and simulate Representative Volume Elements (RVEs) to better understand the influence of such parameters on the mechanical behavior of polymer foams.
Early work of Rusch and Gent [1-2] investigated the mechanical behavior of polymeric foams. However, only few articles are discussing about modeling their microstructure-mechanical properties relationship. The complex foam microstructure displaying heterogeneous morphology is a challenging area for numerical modeling. Experimental testing coupled with tomography are now helping to understand such relations. We can cite work from Weißenborn et al. [3] who modelled 3D X-Ray scanned microstructures using phase-field framework. The authors were able to capture the relation between compression modulus and foam density for values ranging from 200 to 600 kg/m3. Amani et al. [4] also performed finite element modeling on open-cell aluminum foam based on X-ray tomography. A damage elasto-plastic model was used to better understand location of possible zone of fracture in the material. More recently, Vestrum et al. [5] performed tomography based finite element simulations on polypropylene foams. They investigated the effect of the resin material behavior (perfectly plastic or enriched with linear hardening) on the mechanical response of the polymeric foam. They found good agreement with compression tests for an elasto-plastic material model displaying linear hardening behavior.
The study will focus on the development of a digital framework to generate and simulate the mechanical behavior of the polymeric foams from tomography to statistically representative microstructures. The generation and homogenization of these materials will help to better understand the influence of microstructural features on the mechanical behavior of the material. Recently, a FE library, CimLib® ([6-8]), based on anisotropic mesh adaptation and level set methods was developed at the Center of Material Forming (CEMEF) to model heterogeneous material. We plan in this work to use the current capabilities of this library and to extend them for the generation of exact or statistical RVEs of foam microstructure. Numerical methods described in this study focused on immerged or body-fitted strategy (FE context - level set framework - meshing adaptation) for exact and statistical RVEs generation. Classical multidomain lagrangian formulation with an enhanced body-fitted remeshing framework is used to model RVEs deformation. Numerical simulations under tensile and compression loading were performed for different foam microstructures with the aim of better correlating the mechanical response of foams to microstructural morphology. Numerical simulations on RVEs were compared to mechanical tests performed for different stress states (compression and tension) and strain rates.
2 Material
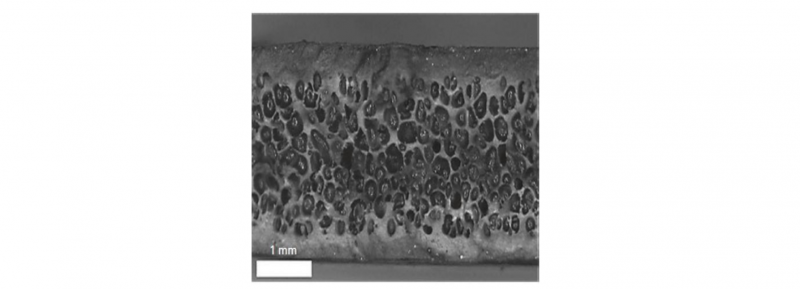
The material investigated in this study is a co-polymer polypropylene SABIC PP108MF10 that is mixed with a chemical blowing agent (CBA). This material is a designed automotive grade polymer commonly used by car manufacturers for bumpers. Plates of different thicknesses were injected using a core-back method. This method is an upgrade of classic injection method. The difference lies in the use of a mold which possesses a moving part (the “core-back”). A force is applied on the core-back to maintain during a short period of time the polymer under pressure. Constant pressure allows the polymer to be maintained directly in contact with the internal molds’ surfaces to solidify without foaming. Then, the mold opens at a fixed velocity which favors the foaming at the center of the part. This technique allows a good surface quality and a controlled foaming process (nucleation and growth of pores). Fig. 1 presents a specific foam microstructure characterized by a foamed core surrounded by two fully dense skins. The ratio of skin to core thickness as well as the pores morphology will have a strong impact on the foam mechanical properties. Three plates with thicknesses of 2.5, 3, and 6 mm were injected. X-Ray tomography scan were performed for the different thicknesses. Tomography observations are displaying different microstructures characterized by specific normal distribution of pores sizes and mean neighbor distance.
Fig. 1. Three layers structure: Skin - Foamed core – Skin.
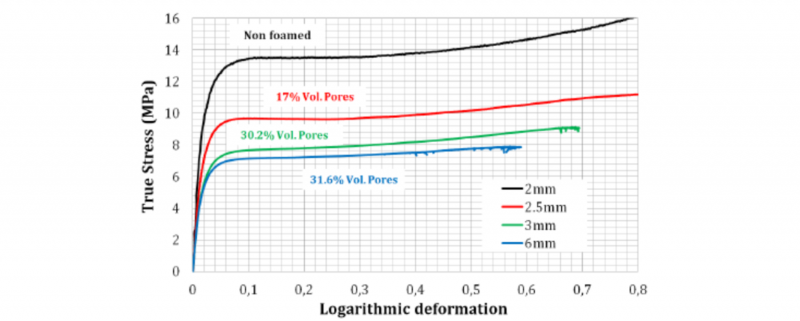
Specimens were then machined along plate thickness. Tensile and compression tests were performed at two different strain rates (10-3 s-1 and 10-2 s-1) at room temperature. Lubricant was used in compression to avoid specimen barreling. 3D Digital image correlation was used to measure the local displacement and strain fields during the tests. True stress and true strain curves were used for building the material database. Fig. 2. presents the mechanical behavior obtained in tension at 10-3 s-1 for different plate thicknesses. We can notice that plates of different thicknesses display distinct mechanical responses that are in relation with the pores volume fraction. More the pores volume fraction is important and more the material stiffness is decreasing. Test results on non-foamed PP are used to identify the resin properties for numerical simulations.
Fig. 2. Mechanical tensile stress-strain curve comparison in tension at 10-3 s-1.
3 Numerical methodology
3.1 Full field methodology
We used in this study numerical tools and methodologies based on a combination of level-set method ([9]) and meshing adaptation tools ([7,8,10,11]. A level-set function, Φ, is defined on a domain Ω. Φ is the signed Euclidean distance function of an interface Γ and any point x of Ω:
Thus, the interface Γ is given by the zero iso-value of the function Φ and by convention Φ is generally defined as positive inside the domain defined by Γ and negative outside. For describing correctly, the interfaces in order to reach accurate computation in the FE method, the mesh is refined around the interface. Meshing adaptation is performed by the mesher/remesher Fitz developed by [7,8] with the metric developed in [12] and adopted in [13].
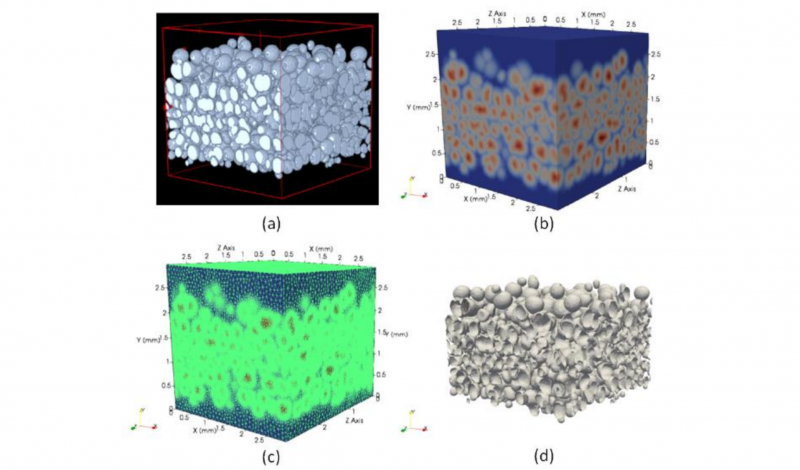
An example of volume reconstruction is given in Fig. 3a. A real microstructure is reconstructed from tomography scans using ImageJ package Fiji. The stack is composed of binary 8-bit images obtained by applying a threshold. Then using Fiji, a signed distance function is determined to scale the distance from the interface. This distance function is then immersed using the Cimlib library inside an initial meshed volume. The first step consists in determining the level-set functions around the interfaces (Fig. 3b) serving as distance function for the mesh metric. Distance functions are then merged into a meshed volume and meshing adaptation/remeshing is performed using Fitz tool developed at CEMEF to discretize accurately the different interfaces (Fig. 3c). In the example, the final meshed volume (25.7 mm3) possesses around 106 million of elements. Fig. 3d displays isosurfaces (Φ(x)=0) representing the interfaces.
RVEs can also be statistically generated from exact microstructure (obtained from X-ray tomography) using a dropping and rolling methods [14,15]. Distribution of pores areas as well as mean nearest neighbor distances between pores is used as inputs to generate such microstructures.
Fig. 3. Full field methodology: (a) X-Ray Tomography; (b) Level-Set reconstruction; (c) Adapted mesh and (d) Pores isosurface (Φ (x) = 0).
For the resin, an elastoplastic model was used as constitutive law. The constitutive equation for the plastic model is based on a Johnson-Cook law for describing the isotropic hardening (Eq. 2). The mechanical behavior of the resin also displays time and stress- state dependency. However, the main purpose of this study was to investigate the capabilities of a simple constitutive behavior regarding the resin for capturing the mechanical behavior of the foam at the microscale level. With this purpose, the strain-rate effect was neglected and the identification was conducted independently for compression and tensile loading as the Johnson-Cook law does not account for stress state sensitivity. However ongoing work is in progress for accounting such phenomena regarding resin mechanical behavior. The slowest strain rate was used to fit model parameters.
where A, B, and n are material parameters, σp is the yield stress, εp is the equivalent plastic strain.
Model parameters for the different media are summarized in Table 1.
Table 1. Model parameters for the different media.
3.2 Boundary conditions and RVE homogenized response
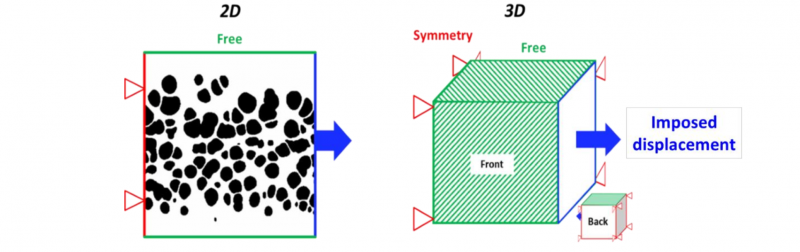
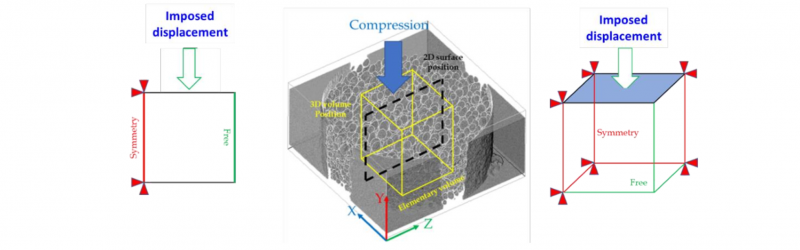
Boundary conditions for tension and compression are presented Figs. 4 and 5, respectively. RVEs represent the microstructure through the overall specimen thickness. Tomography scans were performed in the location of gage length for tensile specimen and over cylindrical specimens for compression tests.
The homogenized response of RVEs in term of equivalent stress (σeq) and strain (εeq) values were calculated by integrating their respective values (σlocal and εlocal) for each element over their volume, V, divided by the total volume of the meshed part (Vtotal) (Eqs. 3 and 4). Equivalent stress-strain curves were used to compare numerical results to experimental tests.
Fig. 4. Boundary conditions of 2D and 3D simulations in tension.
Fig. 5. Boundary conditions of 2D and 3D simulations in compression.
4 Results
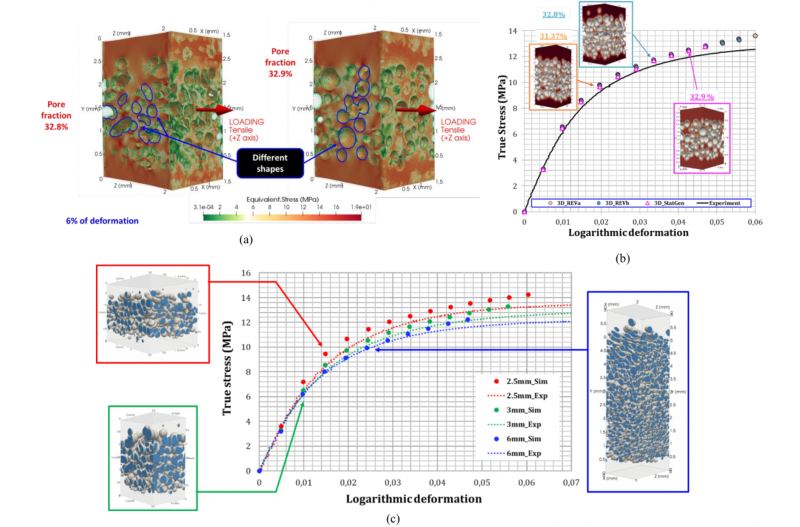
After performing a convergence study on RVE size for each plate thickness, computations were performed. Fig. 6a displays simulations for a real microstructure and statistically generated RVEs for material of 3 mm thickness. Results regarding local stress field are displayed in the figure. We observed that the stress concentrations are mainly located between close pores and for pores “clustering”. Statistically generated RVEs do not account for the complex pores shape exhibited by real microstructures. Only spherical pores are generated. Fig. 6b presents the stress-strain curves for two converged RVEs obtained from a real microstructure compared to a statistically generated one. We can notice a very good agreement meaning that pore shape is not a predominant feature controlling the mechanical properties of the material. We can also observe a good agreement between simulations performed at the mesoscale and experimental tests carried out at the macroscale for both real and statistical RVEs. Fig. 6c displays the mechanical response of RVEs generated from real microstructure compared to tensile tests performed at 10-3 s-1 for the three thicknesses. A good agreement can be observed opening a way for the use of such numerical framework to better understand the relationship between microstructure and mechanical properties.
Fig. 6. a) Local stress field in tension for two different RVEs: the first one generated from real microstructure and the second one corresponding to a statistically generated microstructure; b) Comparison between model and tensile test for plate of 3 mm thickness at 10-3 s-1; c) Comparison between model and tensile test for the three thicknesses at 10-3 s-1.
5 Conclusion
Using a core-back method, three different plate thicknesses were injected (2.5, 3 and 6mm). Each plate was then characterized experimentally in tension and compression for different strain rates. Set of samples was also observed by X-Ray tomography to study their microstructures and generate RVEs. A full-field methodology in 2D and 3D was then used based on immersion and adaptive meshing and remeshing to generate and simulate RVEs from real or statistically based microstructures.
RVEs convergence analysis were performed to determine the optimized volume size for each thickness. Then, 2D and 3D simulations were carried out and compared to experimental data. We noticed that 3D simulations was in good agreement with experimental results whereas 2D simulations tend to underestimate the test results by overestimating the pore fraction. Such methodology providing digital materials may help the foam design to sustain specific material properties.
Acknowledgements
This material was based upon work supported by the Centre Technique Industriel de la Plasturgie et des Composites regarding the collective action focusing on developing new foaming process.