1 Introduction
In the fields of industries, applications of Fiber Reinforced Polymers (FRP) for both structural and non-structural purposes became widespread in the last decades. This led to many experimental and numerical studies about their mechanical behavior as well as in regard to low velocity impact response and related damage mechanisms [1–4]. In addition to the more usual applications of carbon, glass or kevlar fibers with thermosetting polymer matrix like epoxy, the increasing requirements toward the use of less polluting and renewable materials, promoted the growth of the research interest for the adoption of natural-based FRP. Driven by this interest in new eco-sustainable composite materials, in many usages synthetic reinforcing fibers as well as thermosetting matrices, have been gradually replaced respectively by natural fibers and thermoplastic polymers, intrinsically recyclable.
The response of this class of materials resulted in a rapid decrease of mechanical properties together with an increasing of viscous dissipation phenomena when subjected to increasing temperature [5]. This because of the characteristic behavior of thermoplastic polymers toward the transition temperature [6]. Although many experimental studies and numerical investigations about viscoelasticity of polymers were conducted [7,8], little information is available on the numerical modelling of the dynamic response of fiber-reinforced thermoplastic polymers and on the influence of temperature on these aspects. In this work, the response of a basalt fiber-based Nylon 6 (PA6) polymer composite, was numerically modelled under low-velocity impact and validated on the base of an experimental impact campaign. With the purpose to appreciate and model the viscous response of FRP material, drop impact tests under different temperatures (40°C, 80°C and 100°C) and impact energy (5J and 30J) were conducted and reproduced through Finite Element Method (FEM) simulations. On the base of literature proposed models for the viscoelastic response of polymers [6], and with the acquired data about the rheological response of PA6 under different frequency/temperature, a Maxwell material viscoelastic model was implemented to consider the non-linear polymers dissipation. Simulations were conducted to reproduce the impact response in terms of force to deformation curves and impact dissipated energy as well as to evaluate the influence of viscous contributions on the material damage processes.
2 Materials and Methods
2.1 Experimental Methodology
Impact tests were conducted by using a drop tower machine Instron 9350, equipped with a thermostatic chamber and an anti-rebound system. According to the ASTM D7136 international standard, a hemispheric shape impactor of 20 mm diameter and a total mass of 5.4 Kg was dropped from different height to obtain the desired energy level of 5J and 30J. The specimens to be impacted were a 100x150 mm plate with a thickness equal to 2.90±0.1 mm, positioned in the testing area and fixed by clamping its edges. The investigated composite consists of a basalt plain weave type fabric (BS) (areal weight: 210 g/m2) purchased from Incotechnology GmbH (Germany) and Nylon 6 (PA6) Lanxess Durethan B30S (MFI@260 °C, 5 kg: 102 g/10 min, Tg: 51.6 °C and Tm: 223.1 °C). The rheological properties of PA6 in the function of the temperature were estimated through a single cantilever Dynamic Mechanical Analysis (DMA). The test was executed in a frequency range between 0.1 Hz and 100 Hz and for temperature from up to 105°C.
The laminate was obtained with a film stacking technique by alternating PA6 films and Basalt (0°/90°) reinforcing fabrics for a total of 18 plies. The layers, symmetrically stacked with respect to the middle plane, were subjected to a compression step using a lab press Collin P400E under pre-optimized conditions reported elsewhere [9]. The obtained panel presented a fiber volume fraction close to 50%.
Low-velocity impact tests were conducted for 5J and 30J impact energy and for temperatures equals to 40°C, 80°C and 100°C to appreciate the viscous effect on the panel impact response in terms of maximum contact force, maximum panel deflection, dissipated energy and damage occurred. A further test was conducted at room temperature for 30J impact energy to allow the model validation in the condition of purely elastic response.
2.2 Numerical Methodology
A numerical FEM model able to reproduce the BS/PA6 impact response was developed by adopting a commercial Finite Element Analysis (FEA) software. An explicit dynamic algorithm was adopted to run the simulation and no mass/time scaling was introduced in order to not affect the analysis results. As reported in Figure 1, the symmetry of geometry, loads and constraints with respect to the X-Z and Y-Z planes, allowed to model the normal impact of the impactor on the panel adopting a 3D symmetric quarter model. The impactor was obtained as a hemispherical discrete rigid revolution surface, with a diameter of 20 mm, which was meshed by adopting 4-node 3D bilinear rigid quadrilateral elements (R3D4) with a uniform size of 0.4 mm. The panel layup was modelled ply-by-ply with each ply obtained as a 3D solid 50x75x0.165mm meshed using Continuum Shell 8-node quadrilateral elements (SC8R) with reduced integration and hourglass control enhanced. The refinement of the mesh was chosen finer in the impact region, with an element size of 0.4 mm, while a 1.6 mm coarser mesh was imposed to the rest of the panel. The transition between the two elements' size was obtained thanks to a single bias seeding.
For the model assembly, shown in Figure 2, the panel was constrained by suppressing the out of plane displacements and in-plane rotations of the geometry symmetry cutting planes, while all the degrees of freedom were suppressed on the rest of the panel edges. The impactor was constrained by suppressing all the degrees on freedom, less than the Z direction displacement. On a reference point placed in its center of gravity was applied the impact initial velocity in the negative Z direction, easily computed known the drop heigh and the impactor mass. The letter was assigned as a concentrated mass in the reference point itself. For the impactor to panel contact interaction a surface-to-surface properties with a friction coefficient of 0.3 was adopted [2,7].
Figure 1. Perspective view of the impactor and layup panel assembly 3D numerical model.
Known the fiber volume fraction, the elastic instantaneous properties of the plies were computed as the homogenization of basalt fabric and PA6 polymer properties, available on manufacturer material datasheets. At the room temperature the elastic constants, here reported in Table 1, were retained uninfluenced by viscous phenomena, therefore the material behavior is perfectly elastic until the occurrence of brittle fracture. In this regard the basalt fibers were retained not influenced by the temperature and so its contribution to the elastic properties was considered as constant [9].
Table 1. Instantaneous homogenized elastic properties of the lamina at room temperature.
According to the experimental results [10], with the increasing of the temperature, the influence of viscous phenomena become gradually unneglectable for the polymers with the progressive decreasing of the instantaneous values of the elastic properties which also presented a dependency on the application time of the loads.
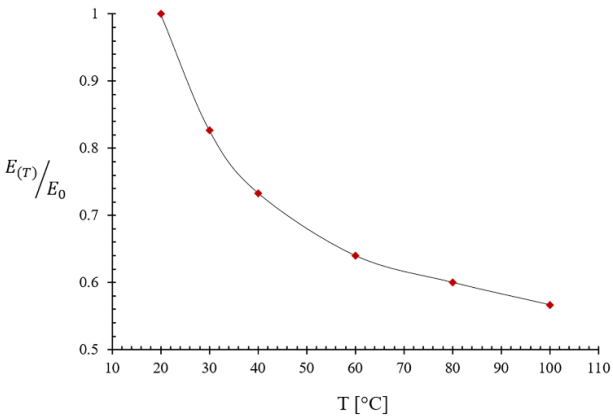
The parametrization of the elastic instantaneous response is reported in Figure 2, where the instantaneous elastic modulus in the function of temperature (E(T)), is reported normalized with respect to its values at room temperature E0.
Figure 2. Instantaneous elastic modulus in the function of temperature (E(T)) normalized with respect to its value at room temperature .
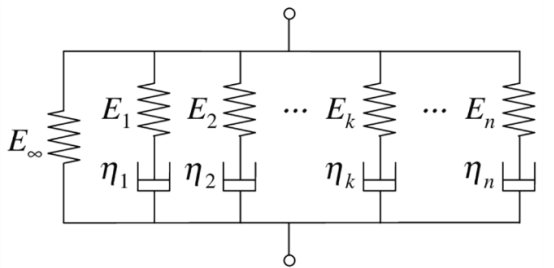
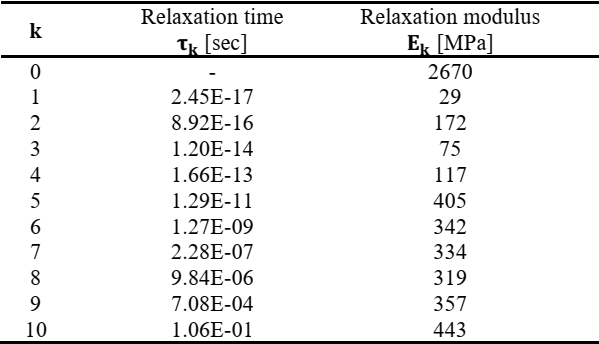
The PA6 rheological behavior was modelled by adopting a generalized Maxwell model [6], shown in Figure 3, with N=10 spring-damper maxwell elements, whose values are reported in Table 2, which allowed to fit the DMA experimental data.
Figure 3. Graphical representation of the generalized Maxwell model.
Table 2. Generalized Maxwell model PA6 relaxation times and elastic modulus.
The presented values properly homogenized with the basalt elastic properties, allowed to consider both the effect of temperature and load history on the overall response of the lamina. The data presented in Table 1 for the room temperature behavior were submitted to the software as temperature-dependent, according to the evolution with temperature exposed in Figure 2 and relaxation phenomena was considered by submitting the data of Table 2 in form of Prony series.
Intralaminar damage was considered by adopting the Hashin damage model with a linear damage evolution [2,11], whose properties are reported in Table 3. The contact among the plies was modelled with a traction-separation contact algorithm by considering damage initiation and evolution to model delamination phenomena [2,12]. According to the literature data about interlaminar modelling [3], the tensile properties for the contact algorithm, in terms of elastic modulus, tensile strength and damage evolution, were considered as equals to the properties of the PA6 polymer.
Table 3. Hashin damage initiation properties.
With the proposed model, simulations for impact energy equals to 5J and 30J were run and each of those was repeated for the experimentally investigated temperatures. Information about maximum contact force, maximum panel deflection and absorbed energy were computed and compared to those ones experimentally measured.
3 Results and Discussion
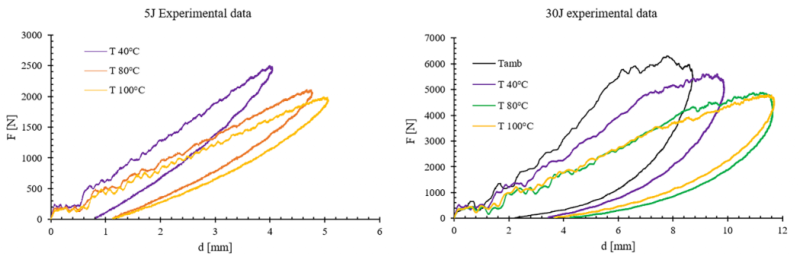
The outcomes of the low-velocity impact experimental activities in terms of contact force to panel deflection curves, for the tested temperatures, for 5J and 30J impact energy, can be seen in Figure 4. Values of maximum impact energy (Umax) and absorbed energy (Ua), with respect to the nominal impact energy (U), together with the maximum impact force (Fmax) and panels deflection (d), were evaluated to be compared to the numerical results.
Figure 4. Force to deformation curve for 5J and 30J impact energy for each tested temperature.
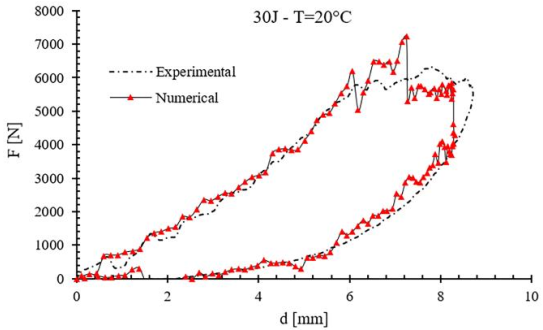
With the purpose to validate the proposed numerical model, only for 30J impact energy, a room temperature (20°C) impact test was conducted. Its comparison with the numerical results, reported in Figure 5, shows how in the condition of purely elastic response the numerical model well reproduces the overall panel impact response. In terms of maximum contact force and deflection, the deviation resulted respectively equals to 11% and 4.5%, while a 3% error resulted in the absorbed impact energy. The higher value of deviation, related to the maximum reached peak of force, is deemed due to the damage energy values associated with the damage evolution which needs to be deeper investigated.
Figure 5. Experimentally and numerically obtained force to deflection curve for 30J impact energy at room temperature (T=20°C).
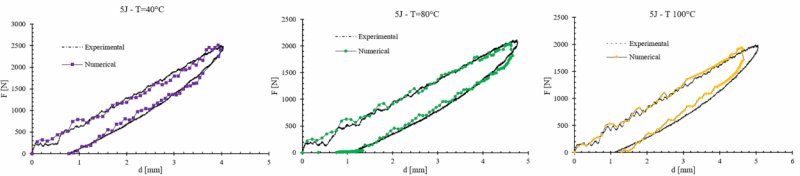
Since the model well describes the room temperature panel impact response, the viscous behavior under higher temperatures were simulated and compared to the experiments. In Figure 6, for each examined temperature, the force to deflection experimental curve is compared to that one numerically obtained for 5J impact energy. According to the experimental evidence, with the increasing of the temperature a progressive reduction of the maximum contact force is associated with the increasing of the deflection values and of the absorbed energy. This letter imputable to the more significant incidence of viscous dissipation.
Figure 6. Experimentally and numerically obtained force to deflection curve for 5J impact energy at 40°C, 80°C and 100°C.
In this very low impact energy condition, the model looks better reproduce the panel behavior, this probably because of the absence of appreciable material intralaminar damage which characterized the presence of the force peak in the presented results about 30J room temperature simulation. The comparison among the evaluated parameters of experimental and numerical results for 5J are shown in Table 4, together with their deviation.
Table 4. BS/PA6 experimental and numerical outcomes for 5J impact energy under the examined temperatures.
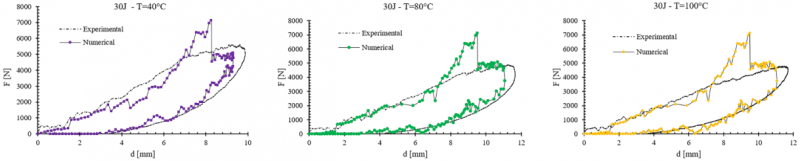
The same comparison was made between experimental and numerical results for 30J impact at 40°C, 80°C and 100°C, as reported in Figure 7.
Figure 7. Experimentally and numerically obtained force to deflection curve for 30J impact energy at 40°C, 80°C and 100°C.
In these last conditions of higher impact energy, the influence of the damage mechanism has a significant effect. As shown in Figure 7, despite the numerical force to deflection curve reproduce the overall panel response, the effect of the brittle interlaminar mechanism implemented produces a stiffer response immediately before the reaching of the peak of force and the consequent occurrence of the in-plane ply damage, followed by a consequent force drop. This model behavior, also detectable in room temperature 30J simulation, presents a more significant deviation with respect to the experimental curve with the increasing of temperature. That is because of the influence of viscous flow on material damage mechanisms which were not considered in the proposed damage mechanism modelling. From the comparison among the evaluated parameters of numerical and experimental results for 30J, shown in Table 5 for each examined temperature, it can be clearly seen how the model presents an overestimation of the maximum reached force while the other values of deflection and absorbed energy presented a very good correlation with the experimental data.
Table 5. BS/PA6 experimental and numerical outcomes for 30J impact energy under the examined temperatures.
For both the impact energies examined, according to the experimental evidence, the values of absorbed energy increase with the temperature with a more significant gap between 40°C and 80°C respect to the gap between 80°C and 100°C. That is because of the polymers transition temperature (Tg = 51.6 °C) which determines a bigger drop of moduli at the turn of that temperature.
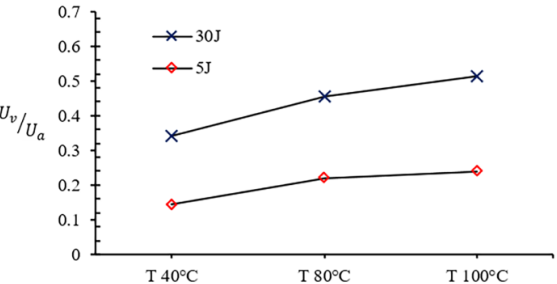
The developed model allowed to evaluate the contribution of viscous dissipation energy (Uν) respect to the total absorbed energy ( Uα).
Figure 8. Viscous absorbed energy normalized with respect to the total absorbed energy for 5J and 30J impact energy for each temperature.
The numerically computed viscous dissipated energy, normalized with respect to the total absorbed energy, is reported in Figure 8 for both the impact energy, and for all the simulated temperatures. An increase in the percentage of the viscous dissipated energy contribution is detectable both with the increasing of the temperature and with the impact energy rising. With respect to the 5J, the 30J simulations independently by the temperature, resulted in greater viscous energy dissipation. That can be explained by considering the total impact time which, due to the decreasing of the material properties, increases with the impact energy.
4 Conclusion
The proposed numerical approach to the modelling of low-velocity impact of thermoplastic polymer-based fiber-reinforced composite under temperature effect showed to well reproduce the overall impact response of the material, thanks to the adoption of a viscoelastic approach able to take into account the viscous dissipation involved. The information about viscous dissipated energy influence, obtained from the model, resulting hard to experimentally estimate, represents an improvement in the low-velocity impact investigation.
Further studies about the modelling of viscous phenomena influence on damage mechanism could allow to correct the maximum contact force determination and precisely estimate the contribution, due to intralaminar and delamination damage, in absorbed energy. In addition, more detailed investigations about the viscoelastic behavior of anisotropic materials are essential to enable a more accurate modelling, by adopting a 3D formulation of the elements instead of the 2D shell elements adopted in this work.