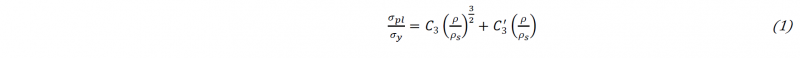1 Introduction

During the last years, metallic sandwich structures have attracted attention for applications in engineering fields, ranging from aerospace structures to transportation industry [1], and different sandwich structures have been studied with different cores such as foams [2,3] and honeycomb [4,5].

Metal foams are very innovative foams, made by cellular structures consisting of solid metal, containing a large volume fraction of gas-filled pores, with properties depending on the metal nature and their morphology [6]. Among metals, the aluminum alloys are largely employed for obtaining foams characterized by relatively high properties, such as low specific weight coupled with high energy absorption capacity, high specific stiffness and reduced thermal and electrical conductivity [7].

There are several ways to produce aluminum foams [8]; a very promising method based on the gas-releasing particle decomposition in semi-solids is known as powder compact melting technique, where an aluminum alloy and a blowing agent in the form of fine particles are mixed and then compacted to obtain the so-called foamable solid precursor [9,10]. Heating the precursor to a little above the melting temperature of the alloy leads the compacted metal matrix in a semi-liquid viscous state; the foaming agent, distributed homogeneously within the metal matrix, decomposes and releases hydrogen, which blows bubbles in the soft alloy. Under these conditions, the released gas forces the melting precursor material to expand, modelling a highly porous structure taking the shape of the mold [11].

In sandwich structures, the core supports the compression stress when deformation occurs, the foam cell edges bend and the foam cell faces carry membrane stresses. The contribution of the cell face stretching to the overall properties of the foam is linearly proportional to the relative density ρ/ρ_s (where ρ and ρ_s are the densities of the foam and of the bulk material of which the foam is constituted, respectively), while the contribution from cell edge bending is non-linear with respect to ρ/ρ_s. Summarizing, so as Gibson and Ashby show in [12], the ratio between the yield strength of a metallic foam in tension (or compression), σ_pl, and the yield strength of the bulk material of which the foam is constituted, σ_y, can be determined by the following equation:

where C₃ and C'₃ are coefficients depending on the cell geometry. A study based on finite element analyses [13] highlighted that the second term dominates for low-density foams.

An extensive analysis of the behavior of different types of aluminum foam was conducted by Idris et al. [14]. They pointed out that Eq. (1) is based on a model of ideal foam and gives only the theoretical collapse strength. Moreover, it provides that defects and irregularities exist: the cell walls are not flat and their thickness is not constant, the foam cells are not of the same shape, size or orientation, some cell walls are missing and the foam density varies, and there are voids and cracks in the cell walls. These factors reduce the theoretical prediction of Eq. (1). Another aim of this work was to determine the influence of the panel thickness on the collapse strength, and in particular for the foam produced by Alulight precursor a decrease in σ_pl resulted in function of the thickness.

Recently, the researchers have been studying the corrugated core sandwich structure, showing excellent mechanical properties. Rejab and Cantwell [15] examined the compression behavior and the failure modes in triangular corrugated core sandwich panels based on three different materials, namely aluminum alloy, glass fiber reinforced plastic and carbon fiber reinforced plastic, respectively. Xiang et al. [16] performed bending tests with various types of thin-walled tubes as core and focused on the relationship between the diameters of the tube and the energy absorption capacity.

Furthermore, Rubino et al. [17,18] investigated the collapse response of sandwich structures with a Y-frame core under distributed and local load, indicating that the Y-frame core sandwich beams have a higher energy absorption efficiency, compared to metal foam sandwich structures.

In addition to the variation of geometric cross section, some studies have been conducted on corrugated core sandwich panels filled by foam. A metallic corrugated core sandwich panel filled with polymeric foam was developed to improve the impact performance, and it was found that the foam filling increases the buckling resistance and the bending stiffness with the decrease of face deformation by more than 50 % [19].

Bahabadi et al. [20] analyzed the debonding in sandwich structures with three different geometries, including simple foam core without any corrugated composite, longitudinal trapezoid and square cores, and manufactured as waved (corrugated) composite core. In another study on the influence of face sheet thickness, corrugation thickness, boundary condition and foam filling on shock mitigation resulted that foam filling reduced the deflection of the panels in all cases [19].

In this paper, the compression behavior of an innovative metal sandwich structure, manufactured without the employment of a mold and consisting of a core in aluminum foam and skins made of stainless steel wire mesh-grid, was analyzed; the wire mesh-grid was also used as mold, in the sense that the aluminum alloy core foamed inside the mesh-grid incorporating it. This flexible solution can offer, among other things, the possibility of manufacturing sandwiches with complex geometries by using localized heating, with consequent customized production and cost-efficiency. Note that regarding the foaming process of precursors by optical heating, Hangai et al. [21] demonstrated the effectiveness of using the steel mesh as die for the manufacture of complex shaped aluminum foam parts, but they did not consider it as reinforcement for foam core sandwich panels. Moreover, quasi-static mechanical tests were performed to determine the adhesion properties of the core/skin coupling and to compare the bending behavior of sandwiches manufactured by innovative and traditional mold [22].

In order to increase the compressive properties of these innovative metal sandwich structures, a corrugated grid, acting as skeleton, was employed inside the core of aluminum foam; this can be considered as a second step following the first step of generating the reinforcement of the structure by the same stainless steel wire mesh-grid as skins. A comparison in terms of compressive yield stress among panels of only metal foam, the sandwich structure with the skins consisting of stainless steel wire mesh-grid and the same sandwich structure with the core in metal foam reinforced by the corrugated grid was carried out.

2 Materials and manufacturing processes

Two types of sandwich structures were manufactured: the first one is characterized by a core in aluminum foam and the skins consisting of a steel mesh-grid reinforcing the same foam; the second one is similar to the first one, but the core in aluminum foam incorporates a corrugated skeleton realized with the same steel mesh-grid used for the skin. For the first type of sandwich structure, three value of thickness were considered: 8, 12 and 16 mm (also referred in the rest of the text as sand8, sand12 and sand16, respectively); while, for the second type (also referred as corrugsand16) only a thickness of 16 mm was considered.

The foamable-solid precursor, consisting of AlSi10 powder mixed with 0.8 wt. % of TiH2 particles, was supplied by Alulight Company. As for the reinforcement, a T-316 0/90 stainless steel wire mesh-grid was employed for its very good resistance to heat and corrosion, because the wire mesh-grid is used also as mold for the foaming process, so it should ensure the stiffness for avoiding its deformation under thermal (heating) and mechanical (foam expansion) loads, the mesh size for obtaining a satisfying core/skin coupling and the strength for reinforcing the foam panels.

A triangular shape was adopted for the corrugated steel mesh-grid; the two source constituents of the sandwich panels and the layout for the sandwich structure with corrugated core before the foaming are reported in Fig. 1, while their main properties are reported in [23].

Fig. 1. Steel mesh-grid and precursor before foaming of the structure with corrugated core.

For both the types of sandwich structure, a piece of grid was cut in order to create a parallelepiped mold in which to place the precursor of aluminum foam. The external dimensions of the parallelepiped were equal to the sandwich panel (70 mm in width and 250 mm in length). For the second type of sandwich, the corrugated skeleton with triangular shape was placed into the parallelepiped together with the precursor.

At this stage, and for both the types of sandwich structures, the foaming processes occurred. It follows the indications of the process investigated by the authors in a previous work, which allowed obtaining aluminum foams with mechanical properties and pore structures similar to the Alulight commercial ones [24]. The charge was placed and left into a preheated 3 kW power muffle furnace. Time and temperature of foaming were estimated according to an experimental campaign of foaming tests; for the first type of sandwich with the core of only foam, a temperature of 660°C and a time of 15 minutes were adopted, while for the second type a temperature of 665°C was set for a time of 18 minutes. At this temperature, the foaming agent expands rapidly; so, small differences in temperature and time are adequate to fill correctly the corrugated grid.

A photograph of a sandwich panel with the corrugated core, after foaming, is reported in Fig. 2.

The density of all the sandwich structures was calculated and the values are reported in Table 1; the quantity of precursor used for all the types of structures was chosen to obtain a theoretical value of foam density ρ= 0.6 g/cm³, but the efficiency of foaming was influenced by the thickness of the structure. In the table, the values of density calculated not considering the weight of the steel mesh grid are also reported; from these values, the density characterizing the metal foam in the core of the structure was estimated.

It is possible to note that the global density of the sandwich decreases as its thickness increases; in particular, a value of 0.9 g/cm³ was found for the sandwich with the thickness of 8 mm. The foaming process was not completed for the precursor in a volume with this low thickness, that was also partially influenced by the presence of the mesh grid acting as a surface of a mold, on which the local pressure hampers the bubbles generation.

3 Uniaxial compression tests

The mechanical behavior of the sandwiches was evaluated by uniaxial compression tests, carried out along the thickness direction, using an MTS Alliance RT/50 testing machine equipped with 50 kN load cell. As the parameter of the test, a speed of 2 mm/min was adopted for all the specimens, whose dimensions were 60×60 mm². Three samples were tested for each type of specimen.

Fig. 2. Sandwich structure with corrugated core.

Table 1. Values of global density of the sandwich structures and density of the metal foam (core of the sandwich structures).

4 Results and discussion

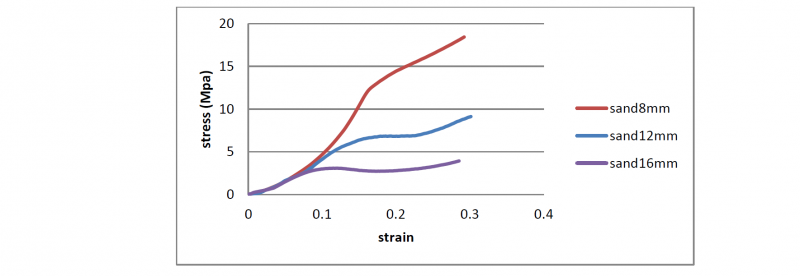
The first set of compression tests concerned the characterization of the sandwich structures realized using the steel mesh grid only as the skins. The results, reported in Fig. 3 (showing example stress-strain curves), confirm that the value of yield stress increases with the density and decreases with the thickness of the sandwich; but the main result is that the value of yield stress for the thicker sandwich structure coincides with the one calculated by (Eq. 1) considering C'₃=0.1 for the constant C'₃, or measured for a metal foam with a density of about 0.6 g/cm³ in [14]. As soon as the thickness decreases, the value of yield stress is influenced by the presence and rigidity of the skins. This result involves that the compression characteristics for these type of sandwich are determined by the properties of the core.

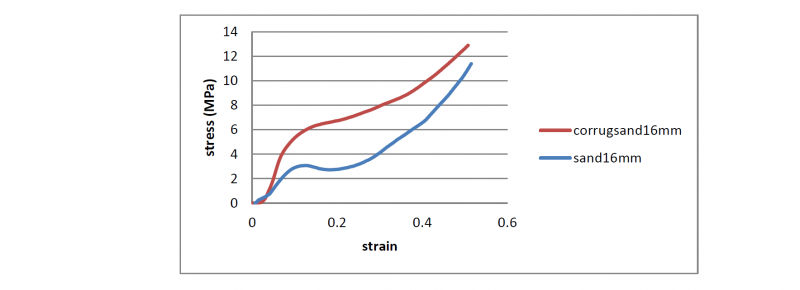
Successively, a comparison regarding the stress-strain curves for the 16 mm thick sandwiches with the core in only metal foam and the corrugated core filled by metal foam is shown in Fig. 4. The increase of the properties for the sandwich with corrugated core is evident observing the figure, from which it results that the steel mesh-grid works very well, and that the trend of the force is completely different for the two types of structures. In the case of the corrugated core, the failure occurs not only for collapse of the voids; in fact, from the photograph reported in Fig. 5 it is possible to note a fracture propagating along the triangular corrugated mesh grid, due to shear stress.

Fig. 3. Stress-strain curves from compression tests on sandwich structures without corrugated core for different thicknesses.

Fig. 4. Comparison between the sandwich structures with a thickness of 16 mm with and without corrugated core.

Fig. 5. Failure propagating in the corrugated core.

5 Conclusions

In this paper, an experimental campaign to evaluate the behavior of sandwich structures manufactured by aluminum alloy foam reinforced with steel grid-mesh was carried out.

Two types of sandwich structure were compared: the first one was realized with skins consisting in steel grid filled by a core in aluminum foam; the second one was realized starting from the first type and including a corrugated steel grid into the core in metal foam.

By compression tests, for the sandwich of first type, an evident decrease of the yield strength results as the thickness of the sandwich increases. For this reason, the second type of sandwich structure was considered and, from the compression tests, an increase of the properties results using the corrugated grid as skeleton of the core of aluminum foam; so this type of configuration becomes particularly advantageous as the thickness of the sandwich structure increases.