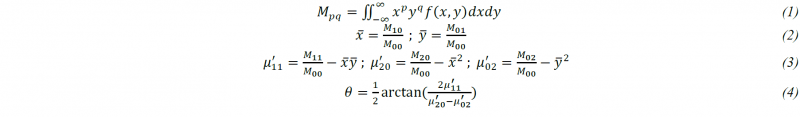1. Introduction

This paper describes and analyzes the material flow in a multi-axis forming process regarding the trajectory influence. Besides other factors, the local material flow in the manufacturing process influences the properties of metallic or fiber-reinforced materials. The ability to influence this material flow provides a process flexibility. For pressing processes, one option to increase this flexibility is to use a motion in more than one dimension [1]. By using all six dimensions for a rigid body motion, multi-axis forming provides an influence on the local material flow via the punch trajectory. Presses with a suitable kinematic like hexapods can realize these punch trajectories [2].

To derive design guidelines for the punch trajectory, the interaction between material flow and trajectory it is of interest. The first step to understand the influence is to observe the material flow in the process. This paper presents an in-situ material flow observation through a transparent die and an image processing.

The influence of different punch trajectories on forming process is studied in a test set-up. Three different punch trajectories are used for one part geometry. Since the part geometry, the punch trajectory and the punch geometry are interconnected, the punch geometry can be derived from the other two by using methods described in [3].

2. Related work

Multi-axis forming originates from using parallel kinematics to perform orbital forming. Recent work on orbital forming focuses on part specific punch tools in an incremental process. The process is enhanced to manufacture non rotary parts on the punch facing side and thereby expand the design freedom for orbital forming [4]. Multi-axis forming shares the local contact area between workpieces and punch while having more design freedom regarding the punch trajectory [2]. To achieve the correct part geometry, the punch geometry is a result of the punch trajectory and part geometry. The process can be either incremental to cyclical cold form metal for example or single stage to form thermoplastic in one continuous movement. Furthermore, variants of one part are possible by slightly altering the punch path.

Multi-axis forming and incremental bulk forming processes are similar concerning regional deformation and the usage of one set of tools within one stage, but differ in the loading cycles, since multi-axis forming has no necessity for multi cycles [5]. There are approaches in incremental bulk metal forming to integrate multiple axes into the process, for example in [6]. By using independent axes to perform a specific tool movement, the flexibility in this approach bases on parallelization and reconfigurability. Multi-axis forming integrates all axes into one parallel kinematic and gains machine and process flexibility [7].

Multi-axis forming also differs from incremental sheet forming. The main differences are the tool geometry and the trajectory. Incremental sheet forming uses mainly translations with a universal tool tip so that the contact can be reduced to a single point path. Contrary to this, multi-axis forming uses translations and rotations with a part and trajectory specific tool [8]. Therefore, the process is not pure die-defined nor pure incremental.

3. Research objective

The research objectives are the analyzation of the material flow and the determination of criteria for path planning of multi-axis forming. In multi-axis forming, the contact situation between punch and material is locally restricted. Multi-axis forming gains productivity from an oblong contact zone perpendicular to the punch progress, which shortens the punch path and minimizes the process time. This separates the process from incremental sheet forming and reduces the path to one dimension of the part length since the other dimension is in simultaneous contact.

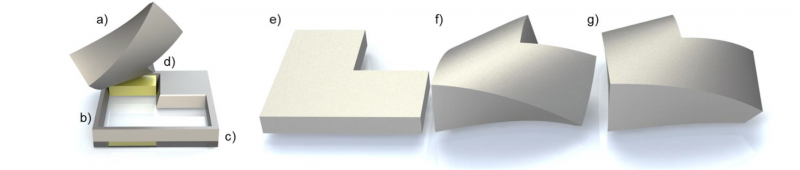
An in-situ measurement concept captures the influences of the punch path on the material flow. For this concept, the measurement observes the forming process for a flat specimen. Since the contact situation between material and punch requires a specific tool for the punch path, three different tools with three paths are developed. This first study uses geometrical simple punch paths with known punch geometries, see Fig. 1. As a reference, a flat punch forms the material with a linear vertical movement in z-axis. A cylindrical punch forms with rolling movement in straight-line diagonal from one edge to the other. The third movement is a rolling movement in curved line and a section of a cone as punch. Each rolling movement starts with a linear movement in z-axis to bring the punch to the start position, see Fig. 1.

Fig. 1. Left: Punch (a) and die (b) with a transparent base (c) and the forming material (d) in yellow at the initial position; Right: Punch geometries from left to right: flat (e), cylindrical (f) and conical (g)

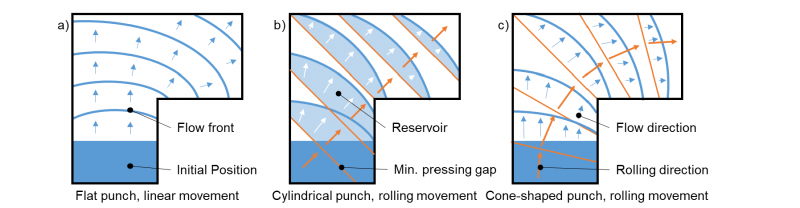
Fig. 2 displays the three schemes of the horizontal material flow within the die. The material flow for a flat specimen predicts a wavelike propagation for a linear forming movement in z-axis. For the rolling movements, these propagations are assumed to be orientated to the current lowest points or line of the punch. With these assumptions of the material flow, the tests are set-up.

Fig. 2. Schematic material flow in a flat, L-shaped specimen for different punch movements: (a) Linear movement in z-axis with a flat punch; (b) Rolling movement in a straight-line with a cylindrical punch; (c) Rolling movement in a curved line with a section of a cone as punch

Besides path length, a criterion for path planning in multi-axis forming is path feasibility. Not every part, punch and path relation is possible. Therefore, this study selects simple paths with known punch geometries and a flat part. For complex combinations, methods to analyze the feasibility are addressed in [3]. Other criteria can be material flow direction and die filling. To understand the relation of punch path to die filling, the die has an obstacle for the material flow in form of an inward edge in the L‑shape. The progress of the die filling is used as scale to compare the local material distribution between each experiment.

4. Experimental set-up

An experimental setup with an optical observation of the forming material measures the material flow in-situ. Therefore, a camera observes the forming material through a transparent die to achieve clear images. This transparent die restricts the size of the process forces. Therefore, plasticine is a suitable forming material for the tests. In this setup, a robot realizes the punch movement and ensures the desired high flexibility for the orientation. The curved punches roll 120° from start to end. The low process forces to form plasticine also suit the capabilities of the robot, here a KUKA IIWA 14. Fig. 3 (a) shows a scheme of the experimental setup.

Fig. 3. (a) Experimental set-up with punch moved by a robot and a transparent die to observe the material flow with a camera; (b) Captured image from below trough the transparent die with the detected edge of the forming material; (c) Center of gravity of the material distribution within a coordinate system and the main direction, the die is segmented in three quadrants (1-3)

Fig 2 (b) is an image taken from the camera perspective. In this figure, the contour of the forming material is highlighted. The contour is determined by filtering hue, saturation and lightness and edge detection on this binary image. In addition, the matrix of the image raw moments M_pq is measured and the center of gravity x̄ and ȳ is analyzed according to [9]. The second order central moments μ are used to determine the main direction of the image axis θ.

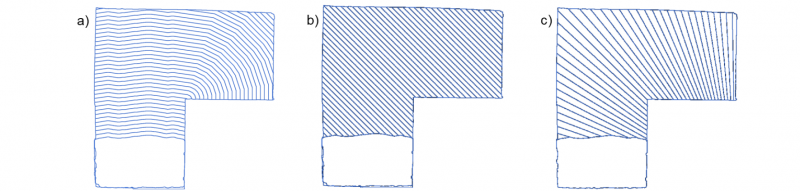
The same algorithms analyzes the schematic material flow from Fig. 2. For the flat punch, a morphological dilation describes the material flow. The first frame of the Fig. 3 (b) is the initial distribution of the forming material. Fig. 4 (a) shows the result of the edge detection after each dilation. For the rolling movement, the material distribution is assumed as an area below a progression line. Here, the line is determined by the lowest points of the punch and is orthogonal to the rolling direction. Fig. 4 (b) displays the contours of the assumed material distribution for a cylindrical punch. While Fig. 4 (c) displays it for a conical punch. Later, the results of the experiments are compared to this first estimation of the material flow.

Fig. 4. Result of the edge detection applied on the calculated material flow for a flat punch (a), a cylindrical punch (b) and a conical punch (c)

5. Results

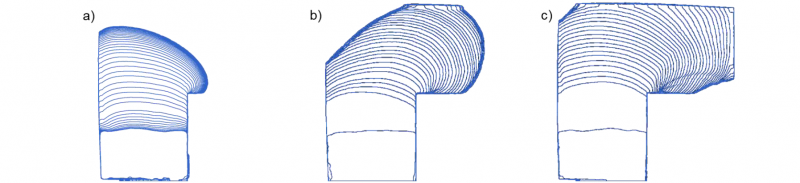
The camera observes the material flow of all three forming variants. The results of the forming tests are contours of the detected material over the process time. Fig. 5 combines the results of the edge detection for 40 frames over process time into one figure. Fig. 5 (a) shows the material flow in the forming process with a flat punch. The material flows homogenously in all directions, stopping at the die boundary and flowing behind the inward edge. Fig. 5 (b) displays the material flow for the rolling movement with a cylinder. For the first four contours, the process is similar to the flat punch as the process starts with the same movement in z-axis. In the rolling phase, the material has a main progression direction in rolling movement. Direct perpendicular to the punch movement, the material flow is limited. Fig. 5 (c) displays the material flow for a rolling movement of a conical punch. Similar to the cylindrical punch, the material flow follows the progression of the punch movement and has nearly no material flow perpendicular to the punch movement.

Fig. 5. Contours of the edge detection of the forming material over the process progress; (a) Flat punch and a linear punch movement; (b) Cylindrical punch with a linear rolling movement; (c) Conical punch with a circular rolling movement

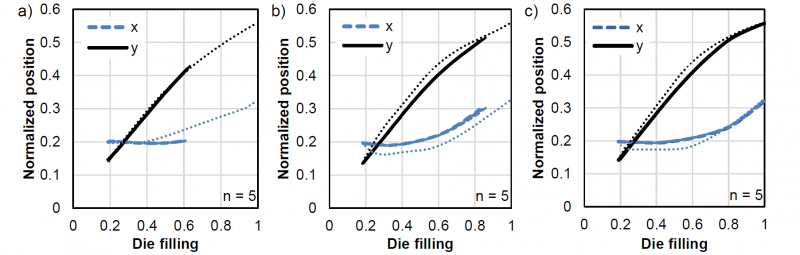
The expansion of the forming material differs over the forming progress between each forming path. Fig. 6 displays this difference through the movement of the center point of the material distribution over the progress of the die filling for five repetitions. The ration between movements in x-axis and y-axis and the shape of the curves differ between each forming movement. In every forming process, the center point starts moving along the y-axis. The differences in y-axis are very small, whereas the progress in x-axis is slower for the flat punch and fastest for the conical punch. Fig. 6 displays the result for an assumed material flow from Fig. 4 in dotted lines.

Fig. 6. Center of gravity of the binary image of the forming material over the process progress; position normalized over the image length; predicted progress in dotted lines; flat punch (a), cylindrical punch (b) and conical punch (c)

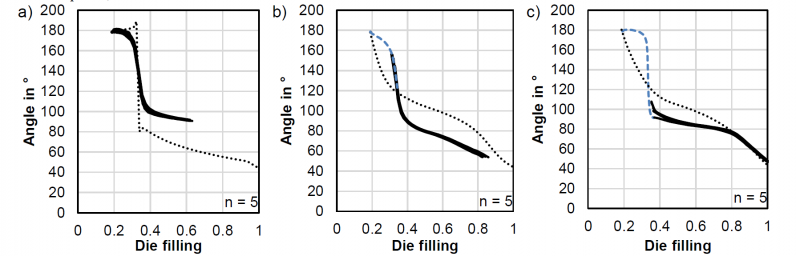
Besides the center of gravity, the direction of the major image axis changes over the measured die filling. Fig. 7 displays the angle of this axis. Since the axis has no direction, the angle is in between 0° and 180°. The initial orientation of the forming material is about 180° and a complete filling of the die would generate an angle of about 45°. The first movement in z-axis is repeated for the cylindrical and conical punch in a separate experiment to analyze the main direction for this movement and generate more data points for this fast changing material distribution.

The forming with the flat punch results in quick change from 180° to about 90°. This corresponds with the filling of the first quadrant of the die, the first third of the die filling progress. The other punch geometries and paths generate a similar angle progress, but differ how fast they strive to the 45° of a complete filling. With the conical punch, the progress to two third die filling has nearly no angle change of the main direction resulting in about 80°, while with the cylindrical punch the main direction changes to about 70°. In the last third of the die filling both punch geometries, cone and cylinder, strive further to the 45°. Only the flat punch stops at 0.6 die filling due to insufficient stiffness and forces of the robot.

Again, Fig. 7 displays the calculated angle of the assumed material flow from Fig. 4 in dotted lines. This assumed material flow has nearly no difference between a cylindrical and conical punch, but differs from the experiments. The angle of the assumed material flow changes faster in the first third of the die filling to lower angles and in the next two thirds slower than the experiments. For the flat punch, this relation is vice versa.

Fig. 7. Angle of the major image axis over the measured die filling; additional measurement for the z-movement in dashed, blue line; assumed progress in dotted lines, flat punch (a), cylindrical punch (b) and conical punch (c)

6. Discussion

The results show differences due to the different punch paths as well as the punch geometries. While the flat punch with only a movement in z-axis leads to a homogenous material flow in all directions, the cylinder or cone shape lead to a directed material flow. Fig. 5 shows exemplarily the difference between the linear and the curved rolling movement in the upper left corner. The conical punch nearly fills this corner with material while the cylindrical punch skips this corner. The movement in y-axis of the conical punch in the first quadrant transports more material into this corner. Therefore, it can be concluded the punch motion path can direct the material flow.

The insertion position and shape of the forming material are identical for each experiment. Under this condition, the scatter of the progress of center of gravity and the main direction of the material distribution is very low. Furthermore, the filling of the first quadrant of the die is quite similar for all experiments, as the first movement in z-axis is the crucial influencing factor. Consequentially, the filling of the first quadrant of the die rather depends on the punch movement than on the punch geometry.

The experimental set-up with the transparent die and an image processing proved suitable as an in-situ measurement. It is possible to determine the material flow in the process. The edge detection captures the material flow indirectly through the overall distribution. Using a robot as press is adequate for the first tests and analyzing process relations. Due to the low stiffness and forces, the punch path is prone to deviations and restricts the experimental capabilities.

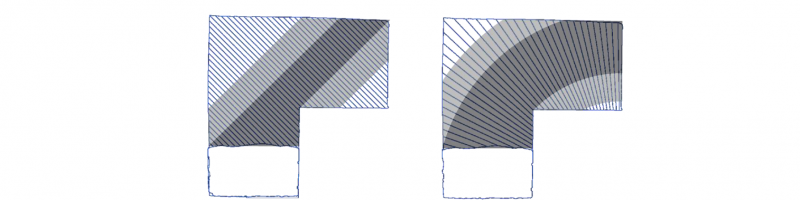
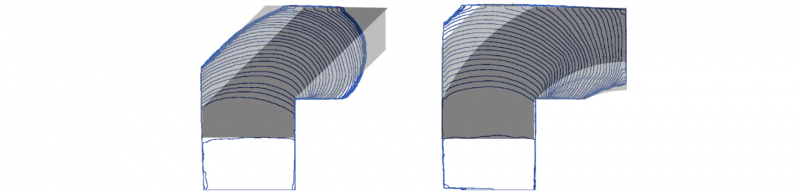
The first estimation of the material flow shows a significant difference to the experimental results. Methods to predict the material flow efficiently can give a feedback for path planning. Predictions should take the material flow along and perpendicular to the forming direction into account. For this purpose, Fig. 8 to Fig. 10 present an enhanced prediction concept. This concept visualizes the material distribution along the punch path until it encounters any obstacle. Starting from the initial position, an area along the punch movement is projected and highlighted in dark gray. To both sides of the main flow direction, a second area is determined as parallel zone and highlighted in light gray. In this zone, the material flow is a superposition of the main flow direction and a flow perpendicular to the punch movement. The exact shape and width of this zone must be determined in future work. Since the initial z-movement has a huge impact, Fig. 10 takes the material distribution after this movement into account. This distribution depends on the overall material volume and the curvature of the punch surface. Here, the distribution is taken from the experiments but must be estimated for a prediction. The prediction in Fig. 10 corresponds with both rolling movements. Although, the authors advice further tests with complex part shapes and punch paths.

A forming simulation can check the planning result. The authors recommend this simulation after the final geometry of the punch is defined. Otherwise, both punch path and geometry lead to a variety of possible simulations.

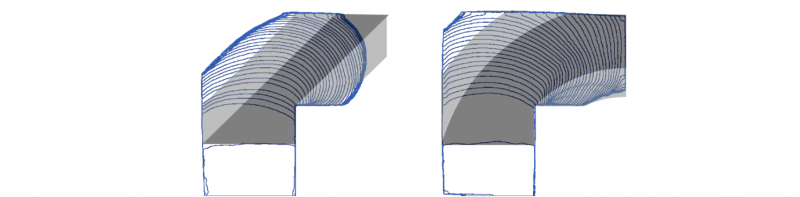
Fig. 8. Estimated material distribution in dark gray by projecting the inserted shape along the punch path; additional material distribution perpendicular to the punch movement with a defined length in light gray

Fig. 9. Comparison between the estimated material distribution and the distribution within the experiments

Fig. 10. Comparison between the estimated material distribution and the distribution within the experiments; Estimation is adjusted to the distribution after the z-movement of the punch

7. Conclusion

The experiments show that it is possible to influence the material flow in forming processes by the path of multi-axis forming movement. A rolling movement fills an L-shaped transparent die. A camera below the die observes the process to capture the material flow for different punch paths. A camera captures the material distribution and an image processing quantifies the distribution via edge detecting. The progress of the center of gravity and the main direction describes the material distribution.

Overall, the main material flow follows the direction of the rolling movement, while only a small part flows perpendicular. This movement can direct the material flow around obstacles like an inward edge. With higher complexity of the part geometry, a trajectory planning process is necessary.

A first estimation of the material flow predicted a distribution corresponding to the progress of the lowest points of the punch. This concept overestimates the die filling. The revised concept estimates a material flow as a projection of the inserted material shape along the punch movement with a finite material flow perpendicular. This revised concept generates a better prediction. The concept takes the material distribution after the first movement in z-axis. Further investigations can optimize the quality of the local material flow prediction.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 318620418. The authors thank Huizhu Ma, Jingpei Zhao and Carsten Ramke for assistance during the experiments and the researchers from the Institute of Forming Technology and Machines at Leibniz University Hannover for the good cooperation in the research project.