1 Introduction

It has been reported that the zygomatic bone is the third most commonly fractured facial area which is also most commonly caused due to traffic accidents [1]. This type of fracture is referred to as maxofacial trauma. The maxofacial trauma is one of the key challenges for public health care services due to a high occurrence rate and high financial cost for the treatments by medication or surgery. Due to the variation in the anatomy of different people, the fracture is not always the same and so there is a variety of different treatments. For example, if the fracture is such that the entire bone structure is broken, then implantation is required.

This paper focuses on reconstructing a patient-specific zygoma implant and predicting the suitability of the implant models made of different biocompatible metallic materials. The paper also addressed identifying a more optimum design which can be 3D printed using the identified biocompatible materials. Implants which match the morphology of the original bones can be manufactured easily using 3D printing. However, validation of the design with regards to compatibility and strength must be done before manufacturing and can be completed using the Finite Element Method (FEM).

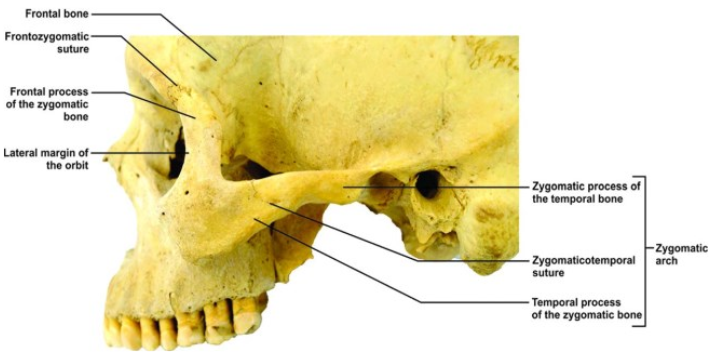Fig 1. Picture of the zygoma anatomy.[3]

The anatomy of the zygoma bone is explained in [2], which describes it as an irregular diamond-shaped single bone that is protruding and forms a prominence of the cheek of the face. It is a single bone constrained by sutures that connect with the frontal, maxilla, temporal and spheroidal bone. The main function of the zygomatic bone understood by medical science is to withstand the forces of mastication (chewing) and transmitting reaction forces from the maxilla [3]. Moreover, it also plays a significant role in maintaining the aesthetic beauty and function of the face and the protection of eyeballs.

According to the FDA, metal implants are chosen over the other biomaterials due to the advantages such as high mechanical strength, durability, good thermal and electrical conductivity, ductility, chemical and biological compatibility [4]. Various additive manufacturing processes have been reviewed, which can manufacture such type of complex structure out of which most feasible, suitable and productive process is the Powder Bed Fusion (PBF) [5]. For the reconstruction of a facial implant, a strategy has been set up as described which is based on the mirror design reconstruction technique [6]. This paper concentrates on the pre-examination of such a manufacturing process which allows the prediction of the results beforehand so that the post-traumatic fracture of zygomatic bone can be treated in a more efficient way by the manufacturing of an actual implant that is compliant and suitable and then can be fitted in the human body during surgery.

2 Material and Methods

Material Properties

First, the initial structural analysis was done using bone material to get the initial results to the permissible stress values on the pillar regions and to measure the allowable stress, stain and deformation of the bone. Then three biocompatible metallic materials,  Ti6Al4V, Stainless steel 316L and CoCr alloy, which are used to manufacture medical implants were used in the models. All the materials were assumed to be linear isotropic homogenous materials. The material properties used in the analysis are as shown in Table 1.

Table 1. Material properties for bone and bone substitute implantable materials.

CT Scan Data Collection

CT scan of an anonymous male patient was provided for the purpose of research by a local hospital in Pune, India. The CT scan was of that of the traumatic fractured zygomatic bone caused due to the road accident in India.  The CT scan data collection was done by the Star Imaging and Research Center, Pune, India on a GE32 Slice CT Scanner. 

Designing or Reconstruction of the bone into an implant    

In Fig. 2, the various steps are described which were followed in the project. The CT scan data was converted to 3d STL file using 3D Slicer software. In the process, 2D CT scans were converted to a 3D model of the craniofacial bone which was done by segmentation using the thresholding technique. Only the bone part of the skull was segmented by putting the threshold value as 100 to 3000. The smoothening effects were enabled to make a smooth model of the bone and the model was saved as STL file format. This STL file was then imported to Autodesk Meshmixer software.

In the reconstruction, aesthetics plays a significant role, the healthy side of the zygomatic area that is left-hand side and the orbital area was mirrored to the defective area which is the right-hand side for maintaining the symmetry of designed implant as shown in the following. After mirroring the region of interest is generated hence the left part of the skull model was cropped by Delete in the select module and the left region was solidified by using Make solid in the Edit module. The above file is saved as an STL file format and imported to the ANSYS Spaceclaim software to import the geometry into ANSYS Mechanical.

The STL files describe only the surface geometry of a three-dimensional object without any representation of colour, texture or other common CAD model attributes. Also, it is not possible to directly conduct a body mesh on the STL file as it is entirely hollow and does not contain any virtual volume and only contains triangular facets on the surface. This geometry must be converted to a solid CAD model to import and conduct analysis in ANSYS Mechanical. The acceptable file formats for ANSYS Mechanical are IGS/IGES or STEP file formats which contain all the CAD attributes.

Hence to convert the STL model into the CAD model a reverse engineering approach was used. First to make an error-free model the STL clean-up was done using the STL clean-up tool which included detecting and fixing the errors such as self-intersections, openings, sharp edges or truncations and over connected edges and vertices.

After that using the CAD model was generated by using the reverse engineering tools such as Auto skin which is a powerful method for auto surfacing to the surface or solid geometry from prismatic or organic shapes. The Auto skin surface tool can also be used to reconstruct the surfaces around faceted data or to modify the geometry of things which are constructed using scanned parts.

This part was saved as an IGS file, which is an acceptable file format and imported in the Ansys Mechanical.   

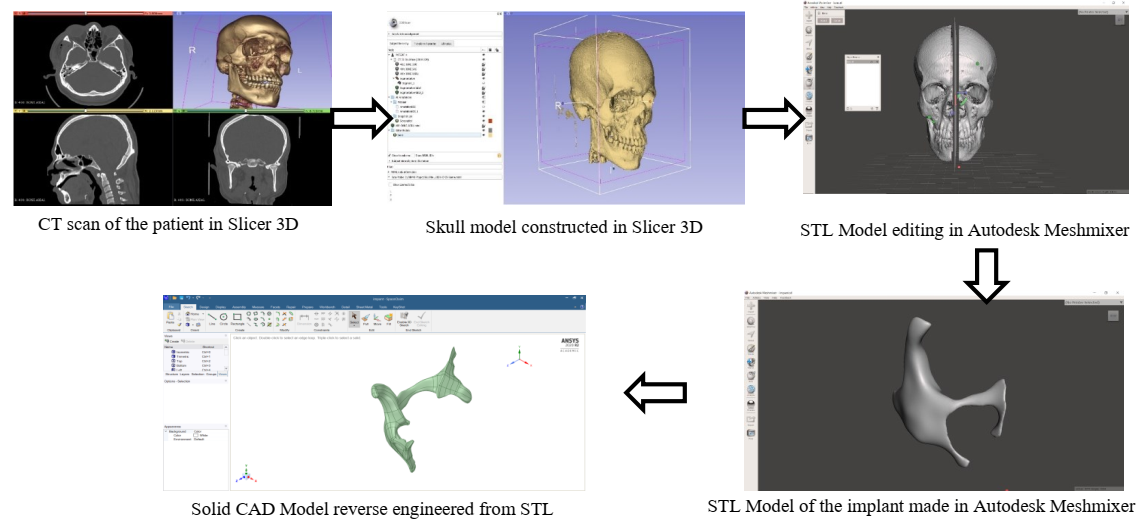Fig. 2. Steps performed in this work to develop the reconstruction of the zygoma bone.

Finite element model

Description

A 3-dimensional static structural analysis was conducted on the generated geometry using ANSYS Workbench Mechanical structural analysis software. In the project as the part generated by reverse engineering contains non-uniform rational basis spline (NURB) surfaces the higher-order 3-dimensional element having quadratic displacement 10 noded tetrahedral elements SOLID187 were used in the mesh. A  total of  19184 elements and 31632 nodes were accommodated in the geometry after mesh convergence tests by plotting the equivalent Von Mises stress at a probe which was positioned near the stress concentration zone where there is an abrupt change in the cross-sectional area in the geometry.

Force and Boundary Conditions

Nodal forces were applied to the inferior surface of the bridge for each of the four models. The named selections were generated to insert the nodal forces. The nodes on which the force is to be applied were selected first where the muscles discussed in the literature are attached to the zygomatic bone. The forces transmit from the muscle due to the mastication process as similar to [7], are as follows.

Table 2: Load magnitudes of human masticatory muscles [7].

The blue regions are the fixed boundaries which were inserted where the attachment of the implant is to be done to the bone and symmetric boundary conditions to the centre sagittal region which is illustrated in Fig 3.

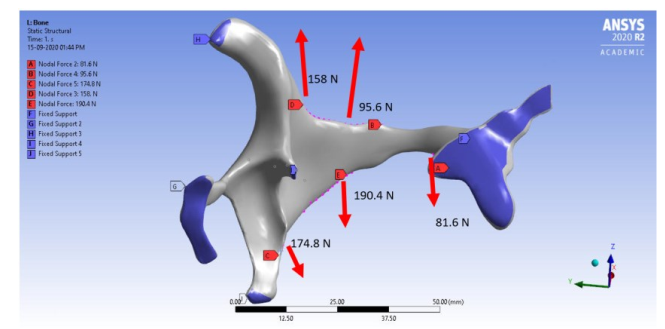Fig. 3. Force and boundary conditions applied to the geometry.

Topology Optimization

To generate different designs in the project topology optimization in ANSYS was used to generate lighter designs. Standard topology optimization was performed to generate three different designs keeping the boundary conditions as same as that of the static structural analysis for the bone, using stress constraint and removing the material from the non-stressed and critical regions where the material cannot remove such as the orbital region of the zygomatic bone the eyeball is present according to the anatomy. The mass removal objectives were set to keep 80%, 75% and 65% of the mass of the material and remove the rest of the material from non-critical and non-fixed areas such as temporal process and the zygomatic process of the zygoma bone region. These geometries were generated in ANSYS Topology Optimization tool and were saved into an STL file format. Then like the reconstructed implant were reverse engineered to create solid CAD models using Ansys Spaceclaim software and were saved in IGS file format that is importable for ANSYS Mechanical Simulation. Same material conditions were inserted for the generated models as described above and same boundary conditions were applied to the regions of the recreated implants and were tested using the same boundary and load conditions using FEA.

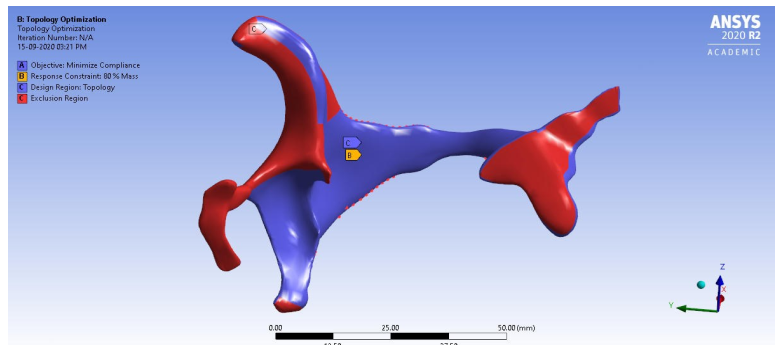Fig.4. Boundary conditions and exclusion regions applied to the geometry for topology optimization.

3 Results and Analysis of Results

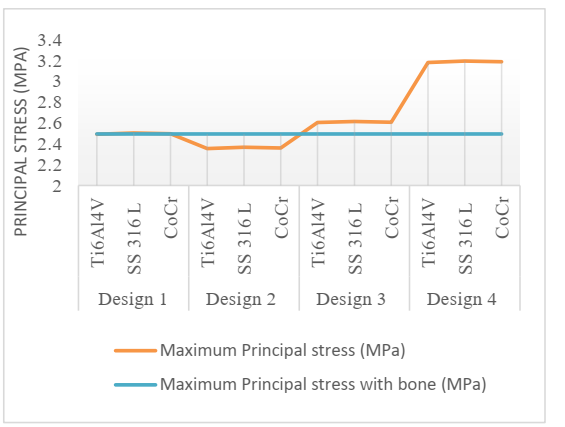
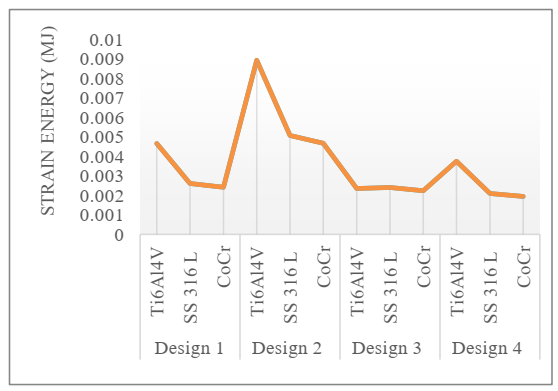
Various responses were calculated using the Finite element method in ANSYS Workbench Mechanical such as Maximum Equivalent Von-Mises Stress, Maximum Principal Stress, Maximum Deformation, Strain Energy and the von Mises and Maximum Principal stresses at the pillar regions such as Zygomatic body, Zygomatic alveolar crest, Zygomatic body, Temporal process of the zygomatic bone, Frontal process of the zygomatic bone, Zygomatic process of the frontal bone. Figures 5 to 8 show the variation of equivalent von Mises stress and Principal stress with the change in material and design with different masses. The graphs in Figure 9 represent the variation of deformation and strain energy.

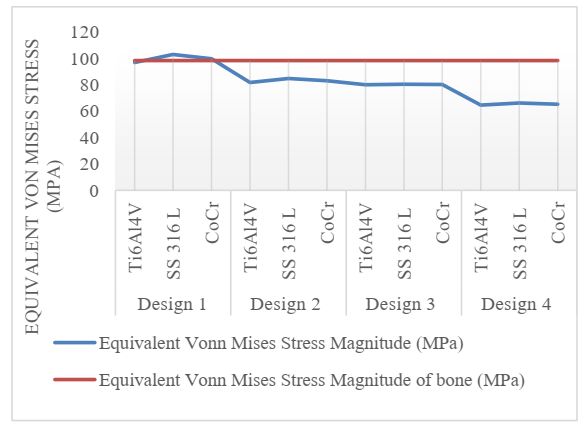Fig 5. Variation of maximum equivalent von-Mises stress.

Fig 6. Variation of maximum principal stress.

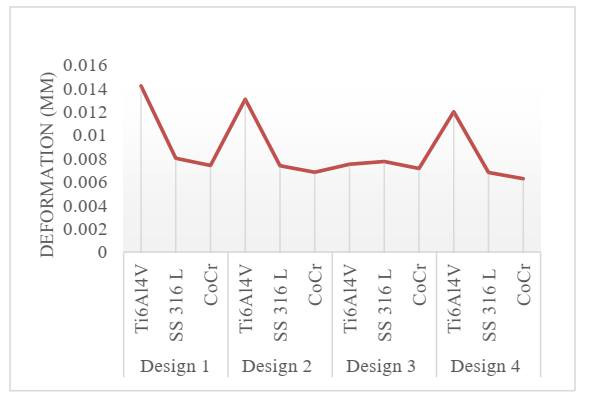Fig 7. Variation of deformation.

Fig 8. Variation of strain energy.

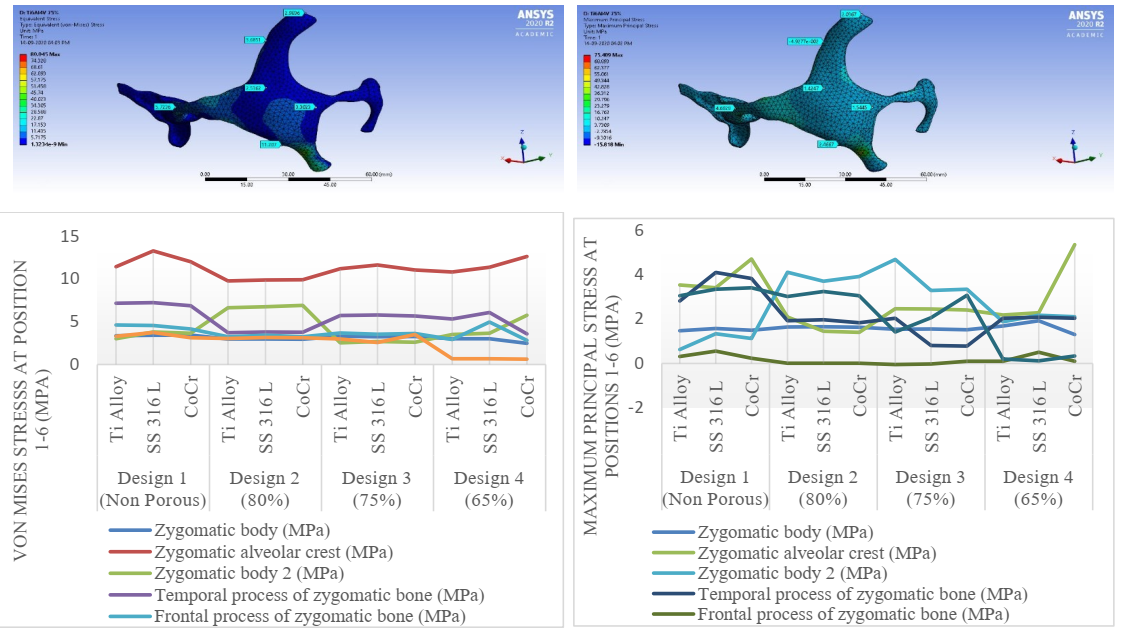Fig 9. Variation of the equivalent von Mises stress and maximum principal stress at the pillar regions.

Analysis of the Results

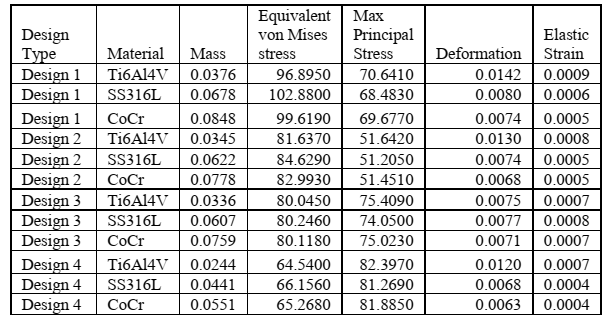
A two-level factorial analysis was conducted using the Taguchi method in which the factors were the material having three different materials and design geometry type which had four different geometries with four different volumes. The responses contained a total of twelve results of the mass calculated, Maximum Equivalent von Mises stress, Maximum Principal Stress, Maximum deformation, Strain energy, maximum elastic strain. For Taguchi Analysis Minitab 18 software was used. Table 3 shows the design matrix having two factors that are design type and material.

Table 3: Results from the two-factor model (design type and material) and corresponding results.

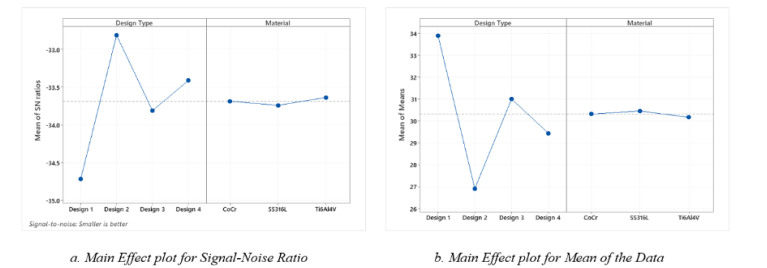
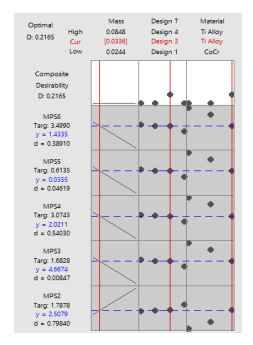
A graphical representation of the relationship between the level of each design parameter and its corresponding impact on performance variation by Taguchi method is shown in Fig 10. From the ANOVA results plotted in Fig 10 a., it can be seen that much lower levels of variation are occurring in the third design. This interaction effect indicates that the relationship between design type and strain energy depends on the material type, see Fig. 11. As the lines are not parallel to each other and meet at Design 3 then it can be concluded there is an interaction between the two factors. For design 3, the minimum deformation occurs for the Ti6Al4V material and the analysis model results indicate that the interaction between design type and material is statistically significant.

Fig 10. Main effect plots for the signal-noise ratio, and the data mean.

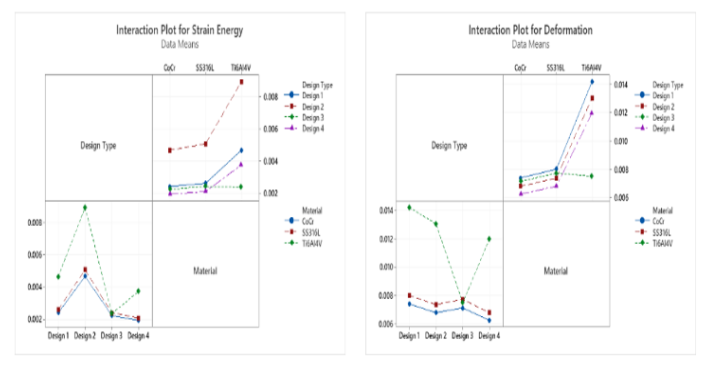Fig 11: Interaction plots for responses of deformation and strain energy.

Response Optimization of the Results

The response optimization simulation was also conducted in Minitab software in order to the selection of the most optimum design and material. In these results, the response variables are Equivalent stress, Deformation, Strain Energy and stresses at zygoma pillar regions. The design parameters are as follows:

•The goal for the response Equivalent stress is to minimize it. A value of 64.54MPa is considered excellent, and values above 102.88 MPa are unacceptable.

•The goal for the response Maximum Principal stress is to minimize it. A value of 51.2050 MPa is considered excellent, and values above 82.397 MPa are unacceptable.

•The goal for the response deformation is also to minimize it. A value above 0.014 mm is unacceptable.

•As the strain energy is the effect of the deformation it is evident that the energy stored should be maximized. Hence the values should not be less than 0.00195 mJ preferably greater than 0.0089 mJ.

•The target value of that of the bone material that was recorded was targeted instead of maximization or minimization. This was done to find out an optimum solution that matches the bone material.

The below graph shows the results from Response optimization that the most optimum design is highlighted in red is Design 3 which has 75% of the mass of the original mass of the part and the most optimum material is Ti Alloy (Ti6Al4V).

Fig 12. Optimization plots showing how the input variable can be optimised for the output response.

4 Conclusion

A 3D Finite element analysis was conducted on four zygoma implant geometries D1, D2, D3, D4 which were generated using the standard topology optimization technique by eliminating the mass of the non-critical sections of the geometry with D1 as non-optimized design. The force and boundary condition used for FEA were modelled from that of actual human mastication which is transmitted by different muscles at different points on the geometry. A data sensitivity analysis was conducted using Taguchi method for the data generated using FEA to investigate the effects of varying parameters on resultant maximum Von Mises stresses, deformation, elastic strain in the material and to fit the data into a statistically relevant model. Analysis of the results suggest that using material Ti6Al4V with design type 3, which was generated using topology optimization using a 25% reduction of mass, was found to be optimum. This can be a potential design/material combination for the implants which can be additively manufactured using powder bed fusion.

This project provides a roadmap of analysing by Finite Element Method which predicts the results for three-dimensional stress analysis problems involving complex geometries and awkward shapes, before manufacturing the actual implant by processes like metal-based additive manufacturing. This has the potential to save a lot of build-test iteration time, material and money. The results plotted could be useful for the design engineers, manufacturers, medical professionals and surgeons to select the optimal material and design for zygomatic bone implants.

 

Acknowledgements

This research is supported by a research grant from Science Foundation Ireland (SFI) under Grant Number 16/RC/3872 and is co-funded under the European Regional Development Fund and by I-Form industry partners.