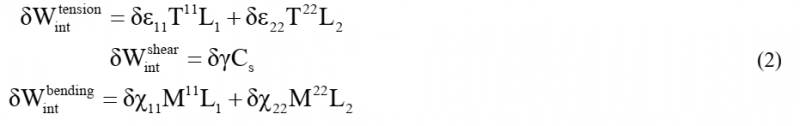1 Introduction

Recently, the textile composite materials, with their high mechanical performance/mass ratio, have been applied in various industries, such as aerospace, aeronautics, transportation and wind power. Multi-layered 2D woven reinforcements, thanks to their low cost, are widely used to manufacture thick composite parts. Nevertheless, the weak through-the-thickness mechanical properties of 2D laminates limit their applications in some crucial areas. In order to reinforce the 2D laminates through their thickness, several technologies, such as stitching, knitting, braiding and tufting, have been developed by inserting the through-the-thickness fibres. The tufting technology studied in this paper is an effective method for the development of 3D preforms.

RTM (resin transfer moulding) [1] is one of the most essential processes in the fabrication of thermoset and thermoplastic resin-based composites. In general, this manufacturing process consists of three main steps: preforming, resin injection, and demoulding. The preforming stage has a significant impact on the quality of the final composite part. Many studies have investigated the defects that arise in the preforming of dry fabrics and the methods and measures to reduce them [2–5]. Recently, several studies were carried out on the formability of multi-layered woven fabrics reinforced along the thickness direction, including the composite preforms reinforced with the tufting technique [6–8]. However, studies on numerical simulation of the tufting technology are limited. In this paper, a modelling approach for the forming simulation of tufted preforms is proposed.

2 Tufting process

Tufting, a relatively novel technology in the field of through-the-thickness reinforcement (TTR), is based on a traditional stitching process that was used initially to make carpets. Tufting is a technique in which reinforcing fibres are inserted in the thickness direction of the multi-layered preform, allowing the layers of the preform to be connected. Thus, it can increase the resistance of the preform to delamination. In comparison to conventional stitching techniques, which require knots to be tied on both sides of the preform, tufting only requires access to one side of the preform. This advantage makes tufting much easier to handle and can be used to reinforce thick structures. As shown in Fig. 1, the thread is tension-free inserted into the dry preform by a tufting needle on one side and then retracted from the preform along the same path. As the needle removes, the thread is retained within the preform by simple friction and forms a loop. This single-sided reinforcement minimizes the impact of the stitch on the in-plane performance of fabrics. The tufting needle and the presser foot on the tufting device are separately controlled by two pneumatic jacks, which enables better control of the penetration length of the needle and the stability of the fabric during the tufting process. A thread feeding device is linked to the tufting needle, ensuring a continuous supply of the tufting thread and also providing a certain degree of tension to the thread.

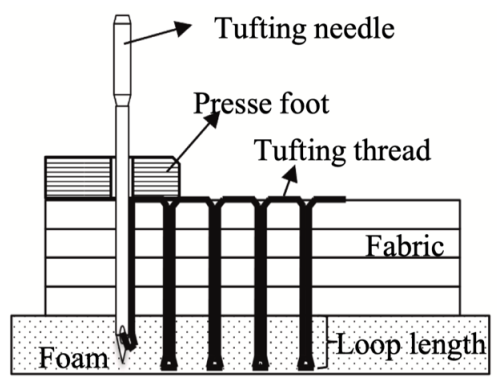Fig. 1. Schema of the tufting process [7].

3 Forming results

Fig. 2. Hemispherical forming of (a) non-tufted and (b) tufted preforms [6].

4 Modelling strategy

Currently, two major types of models are available for textile reinforcements with reinforcing threads, one for NCF (Non-Crimp Fabrics) and the other for stitched preforms. As far as the modelling of NCF is concerned, the challenge is how to simulate the effect of stitches on NCF’s deformation. A meso-macroscopic approach [9], focusing on the layer-to-layer slippage of NCF material during the forming process, is proposed. In this model, the textile reinforcement is modelled by a continuum approach, and the stitching yarn is modelled by 2D rod elements. Besides, a macroscopic model [10], superimposed by two constitutive laws, is proposed for the simulation of the membrane behaviour of NCF. In order to obtain inter-tow deformation, a mesoscopic approach is proposed [11], where tows, stitches, contact and friction of NCF are taken into account. Nevertheless, none of the above-mentioned NCF models can be used directly to simulate the forming of the tufted preform. A tufted preform contains at least two or more layers, whereas the NCF has only two layers at most, which causes the inter-ply sliding of the tufted preform during the forming process more sophisticated. For the modelling of stitched preforms, due to the bilateral knotted connection of the technology of stitching, the position of the stitch is fixed with respect to the reinforcement. A simple model [12] is developed by utilizing rod elements to bind the fabrics together in the direction of thickness, which makes the layers of stitched preform tightly connected. However, the tufted preform is not entirely fixed at both ends; one of its ends is free, which allows slippage between the layers, rendering the stitching model inapplicable.

Fig. 3. Schema of the tufting model.

The modelling strategy for tufted preforms is mainly in the form of a combination of meso- and macroscopic approach, owing to the different dimension of the tufting thread and woven fabric. To simplify the mesoscopic modelling, only the part of the tufting thread in the direction of the thickness (Z-axis) is modelled, and the tufting loop is represented by a single line through the multi-layered reinforcements (Fig. 3). This modelling approach can simulate the interaction of different layers of material with the same line passing through its thickness direction, which is consistent with real physical phenomena. However, unlike the NCF and stitching models, where the interaction between the stitches and the two layers of material is considered, the tufting model needs to manage the interaction between the reinforcing threads and the n-layer material (n ≥ 2). This multi-layered structure of tufted preforms will demand a higher level of robustness and stability of the model.

4.1 Modelling of composite reinforcement

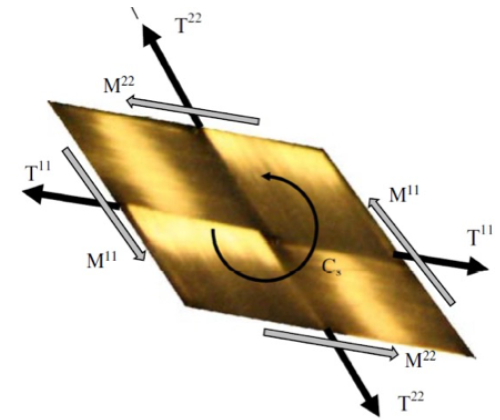
Fig. 4. Stress resultants on a unit woven cell [5].

The internal forces on a representative unit cell (RUC) (Fig. 4) of the woven fabric, in a shell element, is conventionally assumed to be separated into:

Where δW_int ^tension, δW_int ^shear , δW_int ^bending  are the internal virtual works of the tensions, in the warp and weft directions of woven fabrics, the in-plane shear, and the out-of-plane bending. They can be written as:

Where L₁ and L₂ are the length of the RUC in the warp and weft directions. ε₁₁ and ε₂₂ are the axial elongations, γ is the in-plane shear angle between the fibres of two directions, χ₁₁ and χ₂₂ are the curvatures in the warp and weft directions. Their stress resultants are the tensions per unit length in the warp and weft directions T¹¹ and T²² , the in-plane shear moment C_s and the bending moments per unit length in the warp and weft directions M¹¹ and M²². This stress resultant shell approach proposed by Nahiène et al. [13] is adapted to the simulation of textile reinforcement forming.

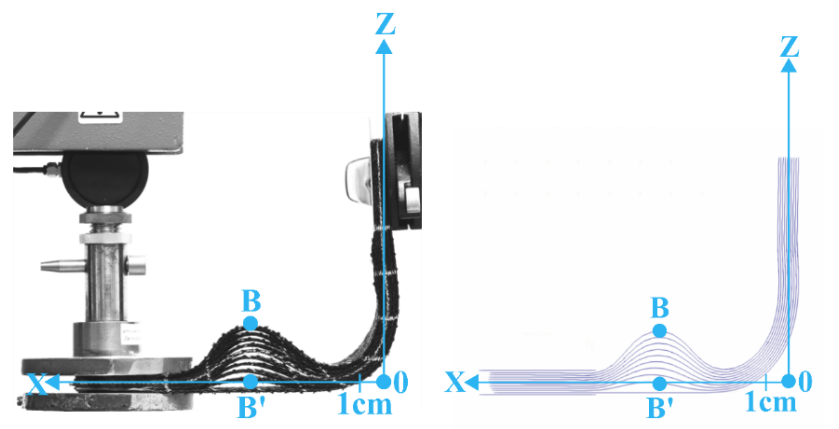 Fig. 5. L-flange forming of a 10 layers composite reinforcements [5].

4.2 Numerical model of tufting

A tufted preform consists of both tufting threads and pinholes. The tufting thread is represented by a chain consisting of rod elements, which is widely applied in the numerical simulation of fibres [14]. The tufting thread can be considered to be quasi-inextensible, and its cross-sectional variation with elongation is negligible. The relationship between the elongation of a tufting thread and the tensile stress is elastic:

Where E is the modulus of the tufting thread.

The pinhole restricts the in-plane movement of the tufting thread while letting the thread to pass through it. In order to reflect the same interaction behaviour in numerical modelling, it is necessary to create a virtual hole in the shell element. At the same time, a specific contact algorithm needs to be integrated between the chain consisting of the rod elements and the virtual hole (Fig. 6). A normal contact force F_N maintains a tight connection between the tufting thread and the pinhole. Moreover, a frictional force F_f along the tangential direction of the tufting thread is also introduced to reflect the influence of the tufting thread on the inter-ply sliding.

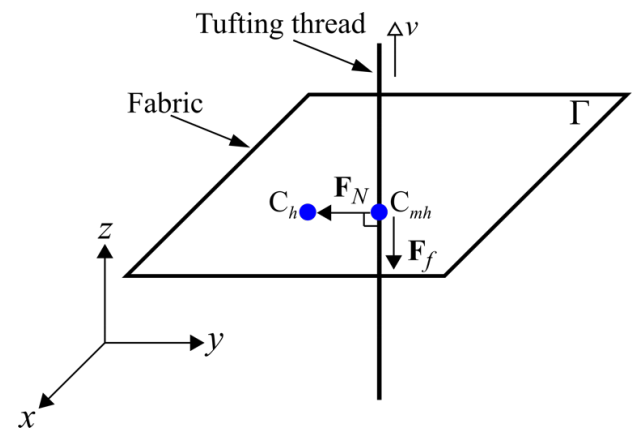Fig. 6. Schema of the specific contact algorithm.

5 Numerical simulation

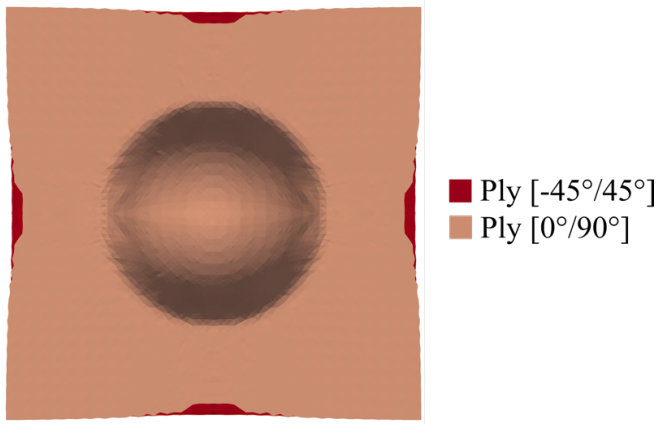Fig. 7. Simulation of the hemispherical forming of tufted preform.

Fig. 7 shows the simulation results of the hemispherical forming of tufted preforms. The restriction effect of the tufting threads on the inter-ply sliding can be well represented by the numerical model.

6 Conclusion

A numerical model was proposed for the simulation of the forming of tufted preforms. The sliding between the tufting thread and woven fabric is controlled by a specific contact algorithm. The hemispherical forming simulation shows the capacity of the tufting model to represent the inter-ply sliding which is significantly modified by the tufting thread.

 

Acknowledgements

The authors wish to thank the National Research Agency (ANR) for funding of this study under the project COMP3DRE "COMPosites 3D REnforcés".