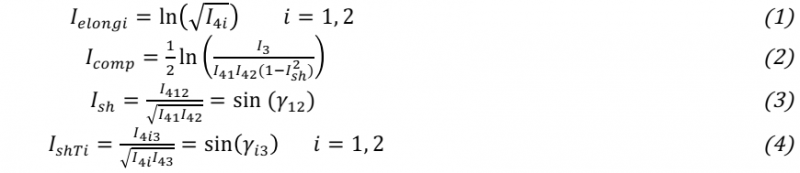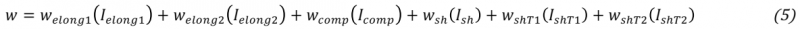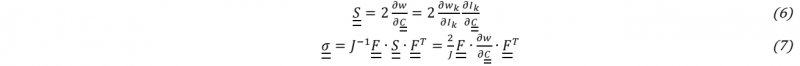1 Introduction

In the manufacturing process of textile composites, especially the RTM process, the forming step is important because it strongly influences the mechanical behavior of the composite in service. In order to better predict the geometrical and mechanical characteristics of composite materials, numerical methods are increasingly developed in view of the duration and cost of testing. Different types of simulations can be distinguished at three different scales: macroscopic, mesoscopic and microscopic. 

For the shaping simulations of woven reinforcements, the approaches are generally carried out at the macroscopic scale [1, 2], in which the reinforcement is considered as a continuous medium. At this scale, it is able to predict the appearance of wrinkles, which is the major defect appearing during this phase [3, 4]. However, some important phenomena may appear only on a smaller scale during a forming process of reinforcements [5-8]. Mesoscopic models, which consider reinforcements as a set of yarns in contact with their neighbors, are able to predict possible defects, such as the rupture and the local buckling of yarns. In addition, the knowledge of the deformations and orientations of the yarns allows to determine the mechanical behaviour of the final part and to calculate the permeability tensor of the deformed reinforcement which can be used to simulate the resin flow in the injection stage [9-11]. Nevertheless, it is very difficult to simulate the shaping of woven reinforcements at this mesoscopic scale for the whole part by taking into account the huge number of yarns and their complex interactions, especially for thick textile composites.

This is why researchers are currently turning to macro-meso simulations of reinforcements. Gatouillat [7] has proposed a simplified model which consists in a mesoscopic scale description of the reinforcements by shell finite elements in contact, allowing the simulation of the fabric on a macroscopic scale, which can predict the wrinkling and sliding of yarns related to the decohesion of the yarns. In Iwata's study [12], visualizations of yarns at the local level of the reinforcement is achieved by coupling a macroscopic simulation of draping and a local simulation at the mesoscopic scale in the positions where the most probable defects are found in the macroscopic simulation. In these models, one of the most critical problems is to compensate for the increase in computing time. In this context, the objective of this paper is therefore to propose an efficient multi-scale method that allows to obtain the deformations and orientations of the yarns for the whole part during the shaping of the woven reinforcements, with a reasonable computation time.

The multi-scale method developed consists in creating a passage of information between the two different scales [13]. This passage makes it possible to transform the deformed information between the macroscopic and mesoscopic scales. In other words, the deformations and orientations of the yarns, as well as the variations of the yarns sections for the whole part can be calculated from macroscopic forming simulations of woven reinforcements. The method is mainly divided into three parts: macroscopic simulation of the woven reinforcements, macro-meso embedded analysis, and local mesoscopic simulation of RVE. Three types of woven reinforcements with different architectures, natures and weaves are studied, and only the data related to orthogonal 3D glass woven reinforcements (Fig. 1) will be presented here.

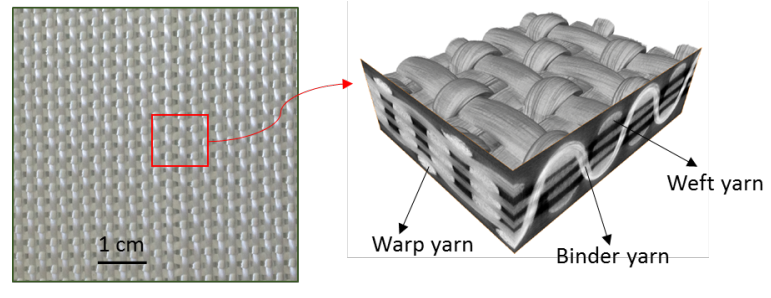Fig. 1. Structure of the 3D non-crimp orthogonal woven fabric and its 3D architecture by X-ray tomography.

2 Macroscopic simulation of woven reinforcements

The first part consists in implementing numerical simulations of the woven reinforcements on a macroscopic scale using the PlastFib [14] numerical simulation tool developed by the LaMCoS laboratory. This finite element code uses a temporal scheme in explicit dynamics. Because of the possible slippage between fibers and yarns, the mechanical behaviors of textile reinforcements are very specific compared to traditional materials such as metals. It leads to a high tensile stiffness in the direction of the fibers compared to other stiffnesses. In macroscopic approaches, woven reinforcements are considered as a continuous medium with a constitutive law of homogeneous behavior. In order to describe the mechanical characteristics of thick textile reinforcements during draping, a 3D hyperelastic behaviour law [15, 16] is applied in macroscopic simulations.

In this law of hyperelastic behaviour, six modes of deformation are considered: elongation of the reinforcement in the warp and weft direction, transverse compression of the reinforcement, shear of the reinforcement in the plane, and transverse shear in the warp and weft direction. For each deformation mode, the corresponding physical invariant based on physical observations of the six above deformation modes can be defined by combinations of the invariants defined in Equation (1-4). I₁, I₂, I₃ are the classical invariants of the right Cauchy-green tensor, and I₄₁, I₄₂ are the mixed invariants concerning to the structural tensors.

The stress-strain relationship is determined through the derivative of a strain energy density. Based on the decoupling hypothesis, the volume energy of deformation can then be expressed as a function of the physical invariants relative to the different modes of deformation. In addition, the contribution of curvature in the hexahedral finite elements is taken into account by adding a local flexural stiffness.

The characterization of the material parameters used in this law are carried out by different classical tests: Tensile test, Transverse Compression, In-Plane Shear, Transverse Shear and Bending test. The identifications are carried out by the direct method or the inverse method with the Levenberg-Marquardt algorithm. Then, the second Piola-Kirchhoff stress tensor S͇ and ̳σ Cauchy stress tensor can be calculated by the differentiation Әw_k/ ӘI_k:

Once the material parameters have been identified, macroscopic finite element simulations can be applied for the woven reinforcements in two cases: three-point bending and hemispherical forming (Fig. 2). Finally, in comparison with the corresponding experiments, the results obtained by simulation are both in good agreement with the experimental ones.

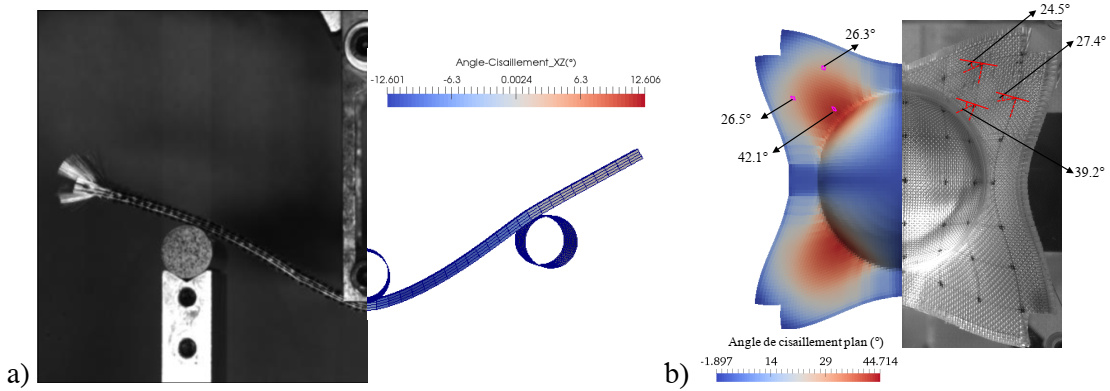Fig. 2. Comparisons between the numerical and experimental results: a) three-point bending and b) hemispherical forming.

3 Macro-meso embedded analysis

3.1 Macro-meso embedded approach

The mesoscopic information of the deformed part is very important for the simulations of the resin flow in the injection stage. Mesoscopic analyses of the entire reinforcement have been performed [5, 12], but the size of the numerical model and the computational time are very important. The objective of the macro-meso embedded approach is to visualize the deformation of the yarns of the whole part during draping with a reasonable computational time. This developed approach proposes to perform mesoscopic analyses using the results obtained at macroscopic scale. If the macroscopic results are relevant, they should be able to provide some basic elements at the mesoscopic scale. In short, the embedded mesoscopic geometry is thus determined from the macroscopic simulation.

The macro-meso embedded approach allows to link macroscopic simulations of interlock reinforcements and mesoscopic modeling of RVEs (Representative Volume Element). For periodic textile reinforcements initially, the geometrical modeling of the RVE is first reconstructed according to X-ray tomography images based on the real geometry of the textile armor (Fig. 3) [17]. As the smallest volume of material, a RVE allows to reconstruct the whole reinforcement by repetitions and translations. The modeling of the entire reinforcement at mesoscopic scale can then be generated in the initial configuration. Then, each mesoscopic node of yarns of the woven reinforcement can be located or integrated into a macroscopic element (Fig. 4). During deformation, the integrated mesoscopic element deforms together with the macroscopic element where this mesoscopic element is located and its mesoscopic nodes have constant coordinates in the reference macroscopic element.

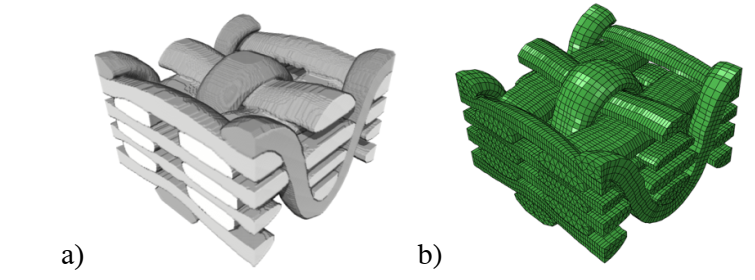Fig. 3. a) Geometry obtained by X-ray tomography of the 3D non-crimp woven reinforcement, b) Corresponding prism mesh.

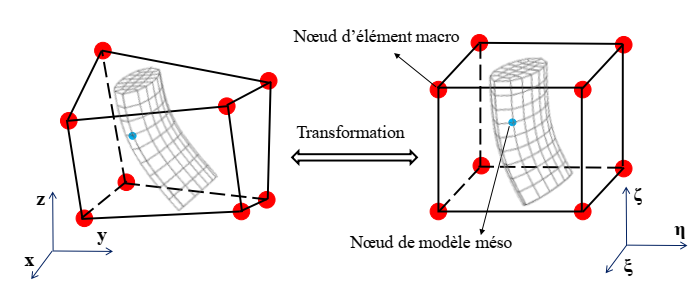Fig. 4. Meso model embedded in a macro element. Real and reference frames.

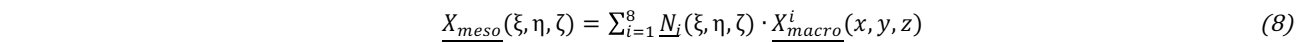
where (ξ, η ,ζ) are the naturel coordinates of the mesoscopic node in the macroscopic reference element. X_meso and X_macro are the spatial coordinates of the mesoscopic node and macroscopic element nodes.

During the transformation, the natural coordinates (ξ, η, ζ) of a mesoscopic node in the corresponding macroscopic element remain identical. In other words, the position of an integrated mesoscopic node remains constant in the macroscopic element. Therefore, the deformation obtained by the macroscopic simulation can provide a first deformed geometry of RVE at the mesoscopic scale in the deformed configuration.

3.2 Applications

Fig. 5 and Figure-6 show the deformed geometries of the reinforcement at the mesoscopic scale obtained by the macro-meso embedded approach in the two cases: three points bending and hemispherical stamping. In addition, the post-treatments associated with each deformation mode: elongation in the warp and weft directions, transverse compression, in-plane shear and transverse shear in the warp and weft directions, are implemented in order to visualize the deformations of yarns.

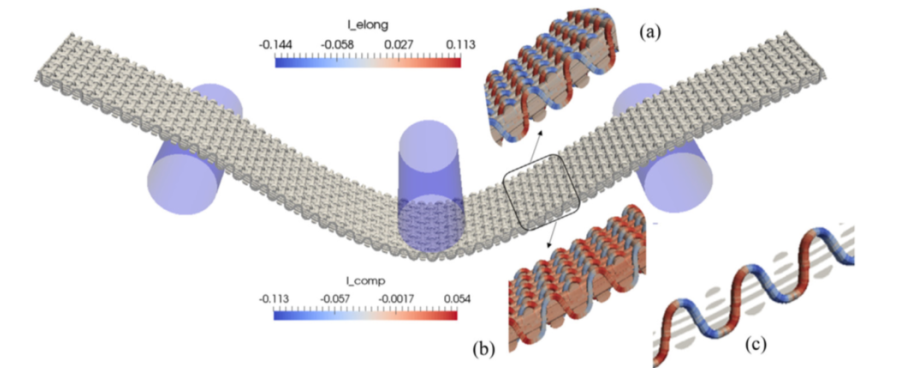Fig. 5. Mesoscopic analysis of three points bending. Physical invariants of yarns: (a) elongation, (b) compaction and (c) elongation in the binder yarn.

The above mesoscopic results on the basis of macroscopic simulations allow to determine the deformations of the yarns, their final orientations and also the voids in an elementary cell. These results can be used for the calculation of the permeability during the next step of resin injection. The calculations concern only geometrical calculations, the calculation time is very fast, from a few minutes to one hour depending on the reinforcement size. This may be sufficient for some mesoscopic scale analyses. Nevertheless, as shown in the figure, it generally has drawbacks, in particular excessive elongation of yarns. A local mesoscopic analysis below can avoid these problems.

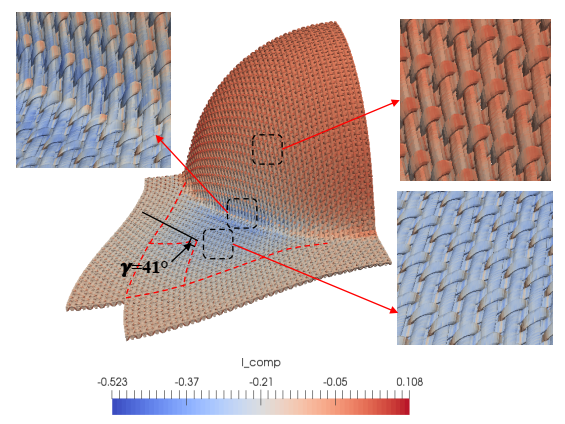Fig. 6. Mesoscopic analysis of hemispherical stamping. Physical invariants of yarns: compaction.

4 Local mesoscopic simulation

As mentioned above, mesoscopic analyses of the woven reinforcement obtained by the macro-meso embedded approach have shown their efficiency in providing a mesoscopic scale solution during shaping. However, the equations of mechanics at the mesoscopic scale are not strictly verified. The mesoscopic recessed deformed mesoscopic configuration is not obtained by solving a mechanical problem but is directly deduced from the macroscopic analysis, due to the assumptions on the continuous medium and the finite element approach. From the point of view of the constitutive law, the stresses do not check the local equilibrium. This approach can lead to excessive elongations of the yarns because it does not take into account local slippage between the yarns. To overcome this difficulty, a local mesoscopic simulation based on macroscopic analysis and embedded mesoscopic analysis is proposed.

The mesoscopic simulation is performed on a local area (e.g. a RVE) based on the results of the macro-meso embedded approach. The deformed configuration obtained by the embedded mesoscopic simulation constitutes the initial state of the local mesoscopic simulation via the boundary conditions in displacement. Then, the displacements imposed on all nodes are released by embedding the edges of the RVE. A relatively simple transverse isotropic hyperelastic behaviour law (neo-hookean) is used to describe the mechanical behaviour of the yarns [18, 19]. Consequently, stress equilibrium is generally achieved within the yarns. The results obtained by the local mesoscopic simulation are compared with those of the macro-meso embedded approach for the two cases: three points bending and hemispherical forming (Fig. 7 and Fig. 8).

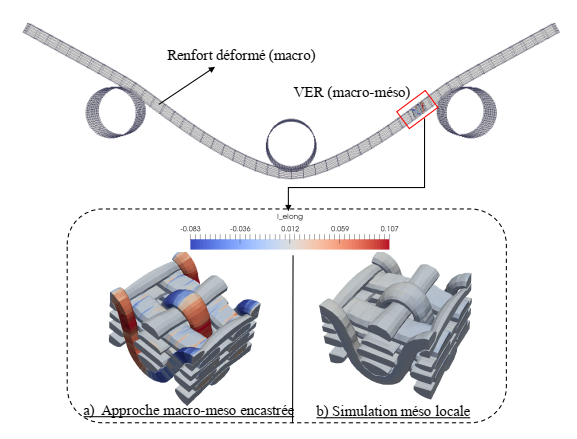Fig. 7. Three points bending: mesoscopic simulations of a RVE. Elongation in a) macro-meso embedded analysis b) local mesoscopic simulation analysis.

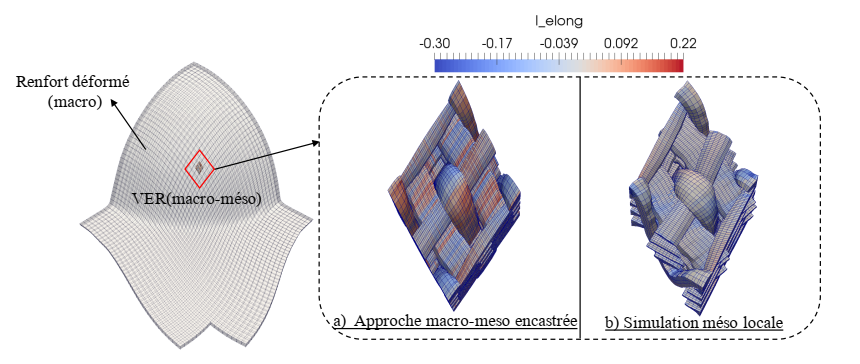Fig. 8. Hemispherical forming: mesoscopic simulations of a RVE. Elongation in a) macro-meso embedded analysis b) local mesoscopic simulation analysis.

The elongation of ten elements located in different areas of this RVE is shown in Fig. 9 for three points bending and Fig. 10 for hemispherical forming. This shows that parasitic elongations in the macro-meso embedded approach are globally suppressed by the local mesoscopic simulation.

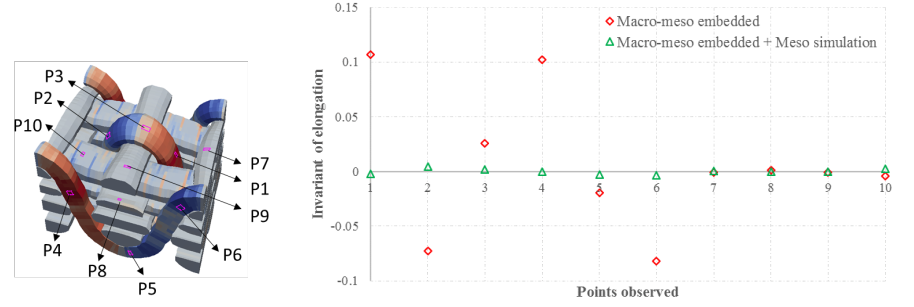
Fig. 9. Elongation change of different locations of a RVE in local mesoscopic simulation for three points bending.

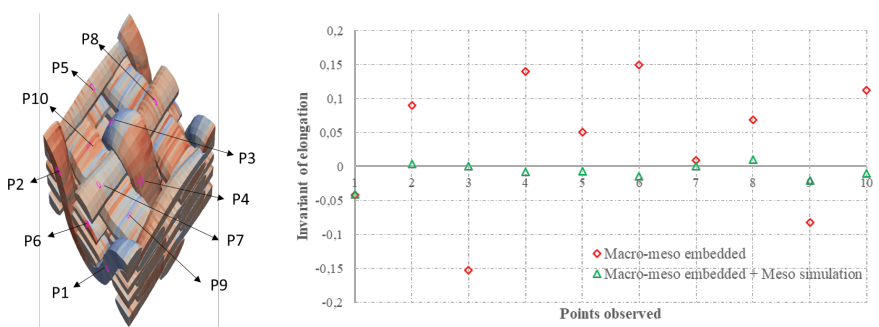Fig. 10. Elongation change of different locations of a RVE in local mesoscopic simulation for hemispherical forming.

Finally, mesoscopic numerical results are compared with experimental results. The deformations of the longitudinal and transverse sections of the yarns can be observed and analyzed by a microscope. In comparison with the experimental results (Fig. 11 b), it can be seen that the numerical results (Fig. 11 a) based on the multi-scale method are in good agreement with the experimental ones from regarding the deformed geometry.

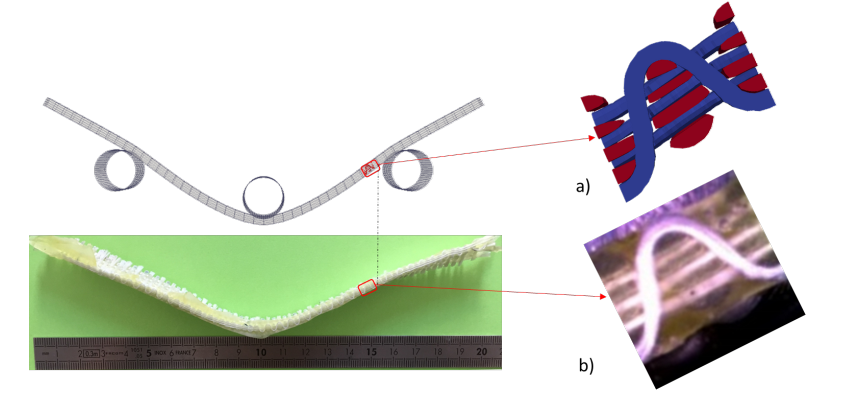
Fig. 11. Woven unit cells in the same position obtained by: a) Local mesoscopic simulation b) experiment.

5 Conclusions

The deformation information of woven reinforcements on the mesoscopic scale is essential to evaluate the mechanical properties of the final composite part, as well as to simulate resin flow during the next injection step. The first macro-meso embedded method proposed allows to obtain mesoscopic scale deformations of the woven reinforcements during forming. However, it has drawbacks, especially excessive elongation of the yarns. To overcome this problem, local mesoscopic simulation based on the results obtained by macro-meso embedded method is carried out by defining specific boundary conditions. This step takes a reasonable computational cost. The results are satisfactory by comparing with the experiment. In addition, some other work is carrying out to optimize and verifier this multi-scale method, such as the study of influences of the number and the positions of RVEs, comparison with the full meso simulation at large scale.