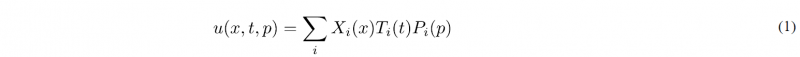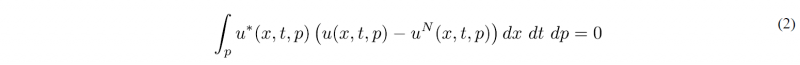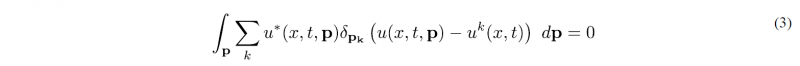1 Introduction

Nowadays, engineering applications concern extremely large and complex systems, where simulation is not only involved in the design stage for evaluating the performances related to the nominal loadings. In nowadays engineering applications, simulation is expected to enable learning, monitoring to anticipate fortuitus events, to take the adequate decisions under the stringent real-time constraint. Thus, the two main arts that characterized the XX’s century engineering, the arts of modelling and simulation, are expected to lead to a new third art, the one of decision-making.

For that purpose, one must predict quick and well, and these two words were historically opposite: to be fast, models were simplified with the associate loss of accuracy, and to be well, fine calculations compromised real-time decisions. Nowadays physics can be solved in almost real-time, for example by using model order reduction, and accuracy of standard models can be improved from the collected data manipulated by using adequate artificial intelligence -AI- techniques, when possible physics-aware. This hybrid paradigm is at the origin of numerous success stories in engineering and technology.

Hybrid twin combines physics in real-time with a data-driven enrichment to enhance accuracy, the last also operating under the stringent real-time constraint and based on as scarce data as possible (frugality). In the work we are focusing on the first topic, the one of physics in real-time, by invoking advanced model order reduction techniques. The second part of the present work will address the challenge of enriching models from data under the real-time constraint.

2 Methods

2.1 Model Order Reduction

Model Order Reduction- MOR - techniques express the solution of a given problem (PDE for instance) into a reduced basis with strong physical or mathematical content. Sometimes these bases are extracted from some solutions of the problem at hand performed offline (e.g. by invoking the proper orthogonal decomposition -POD- or the reduced bases method -RB-). Now, when operating within the reduced basis, the solution complexity scales with the size of this basis, in general much smaller than the size of the multi-purpose approximation basis associated with the finite element method -FEM- whose size scales with the number of nodes in the mesh that discretizes the domain in which the physical problem is defined.

Even if the use of a reduced basis implies a certain loss of generality, it enables impressive computing time savings, and as soon as the problems solution continues living in the space spanned by the reduced basis, the computed solution remains accurate. Obviously, there is no miracle: as soon as one is interested in a solution that cannot be accurately approximated into the space spanned by that reduced basis, the solution will be computed fast, but its accuracy is expected being poor, there is no free lunch.

As soon as the computational complexity remains reduced, these MOR computational procedures can be embedded in light computing devices, such as deployed systems. The main drawbacks of those technologies are: (i) their limited generality just discussed; (ii) the difficulties of addressing nonlinear models, fact that requires the use of advanced strategies (empirical interpolations for instance); and (iii) their intrusive character with respect to their use within existing commercial software.

To circumvent, or at least alleviate, the just referred computational issues, an appealing route consists in constructing the reduced basis and solving the problem simultaneously, as the Proper Generalized Decomposition – PGD- performs. However, this option is even more intrusive that the ones referred above. Thus, non-intrusive PGD procedures were proposed. They construct the parametric solution of the parametric problem from a number of high-fidelity solutions performed offline, for different choices of the model parameters. Among these techniques we can mention the SSL that considers hierarchical separated bases for interpolating the precomputed solutions, or its sparse counterpart, the so-called sPGD.

The most recent variants of the sPGD consists of its sparse regularization, called s2PGD, as well as the multi-sPGD that addresses nonlinear manifolds from a number of locally linear sparse approximations. Finally, to enhance convergence, anchored-ANOVA was combined with s2PGD, where the orthogonality of ANOVA-based decompositions was combined with the frugality of s2PGD to address the ANOVA’s terms involving rich variable correlations.

Once the parametric solution of the problem at hand is available, it can be particularized online for any choice of the model parameters, enabling simulation, optimization, inverse analysis, uncertainty propagation, simulation-based control, ... all them under the stringent real-time constraint. Some papers detailing the just referred techniques are [1-6]. The interested reader can refer to them as well as to the abundant refences therein.

2.2 From SSL to sPGD

We consider the general case in which a transient parametric solution is searched. For the sake of notational simplicity, we consider that only one parameter is involved in the model, its generalization to many parameters is straightforward. The searched solution can be written as u(x,t,p), p being the parameter.

SSL [3] considers a hierarchical basis of the parametric domain. The associated collocation points (the Gauss-Lobatto-Chebyshev) and the associated functions will be noted respectively by p_i,j and N_i,j(p), where index “i” refers to the point at level “j”. At the first level j=0, there are only two points that corresponds to the minimum and maximum value of the parameter p, p_1,0 and p_2,0, defining the parametric domain, with the associated functions N_1,0(p) and N_2,0(p).

If we assume that a direct solver is available, i.e. a computer software able to compute the transient solution as soon as the value of the parameter has been specified, with those solutions noted by u_i,j(x,t)=u(x,t,p_i,j), then, the solution at level j=0 could be approximated from u⁰(x,t,p)= u_1,0(x,t)N_1,0(p)+u_2,0(x,t)N_2,0(p), that in fact consists of a standard linear approximation because at level j=0 the two approximation functions N_1,0(p) and N_2,0(p) are linear, the former taking a unit value at p_1,0 while vanishing at p_2,0, and the last vanishing p_1,0 while reaching a unit value at p_2,0.

At level j=1 there is only one-point p_1,1 located just in the middle of the parametric domain, with the associated function N_1,1(p) that consists of a parabola vanishing at p_1,0 and p_2,0 and taking a unit value at p_1,1 (hierarchical).

Now, the solution u_1,1(x,t) will contain a part already described by the solution at the previous level, that is, u⁰(x,t,p_1,1), fact that allows defining the so-called surplus Δ₁(x,t)=u_1,1(x,t)- u⁰(x,t,p_1,1), that allows defining the first level approximation by adding to the zero level the surplus affected to the its approximation function, i.e. u¹(x,t,p)= u⁰(x,t,p)+Δ₁(x,t)N_1,1(p). The process continues for the next levels of the hierarchical procedure.

An important aspect is that the norm of the “surplus” can be used as a local error indicator, and then, when adding a level does not contribute sufficiently, the sampling process can be stopped.

The computed solution at level j=N, u^N(x,t,p), assumes a separated representation; however, it could contain too many terms. In these circumstances, a post-compression takes place by looking for a more compact separated representation [1]

by enforcing

In the multiparametric case, the same rationale applies. If for example we consider two-parameters (p and q), the zero level is composed of the cartesian product of (p_1,0,p_2,0) and (q_1,0,q_2,0), that results in four points at which high-fidelity solutions must be computed. Thus, in general when having P parameters, the zero level needs for the solution of 2 power P high-fidelity problems to calculate the associated zero-level multi-linear solution.

When moving to the level j=1, it involves (p_1,0,p_2,0) with q_1,0 and p_1,1 with (q_1,0,q_2,0). It is important to note that the data-point p_1,1 with q_1,1 is in fact a point in level j=2.

The previous analysis defines the domain of application of the SSL, in general to address few parameters and low approximation degree. To move forward (multi-parametric and higher degrees), a sparse collocation was proposed, the so-called sPGD.

The sPGD [5] considers a random sampling of the parametric space, p_k (where p is the vector containing the different model parameters), and computes for each of the sampling points, p_k, the high-fidelity solution u^k(x,t)=u(x,t,p_k). Then a separated solution in the general form (1), but now involving each of the parameters in p, is searched from the collocation form

where the functions involved in the parametric dimensions of the separated form, are globally defined to avoid rank-deficiency (global polynomials or kriging), and where to avoid overfitting (when using global polynomial functions) an adaptive enrichment is considered, by assuming that the first modes in the separated decomposition (1) contains the lowest polynomial degrees, with the degree increasing when considering additional modes. This technology computes quite accurate non-oscillating solutions with a complexity (size of the sampling) scaling with the number of parameters, however the procedure considered to avoid overfitting tends to over-smooth the approximation, failing to capture localized behaviors.

2.3 Advanced technologies

Trying to remediate the just discussed drawbacks, the too rich sampling of the hierarchical SSL and the too smooth approximations provided by the sPGD, s2PGD was proposed. S2PGD considers: (i) separated representations, like (1) to operate in multiparametric settings; (ii) the sparse collocation constructor (3); (iii) however, to enhance accuracy while avoiding overfitting, s2PGD consider richer approximation basis, and employs in the construction of the separated representation a L1 regularization in order to keep the approximation as sparse as possible. This regularization can be enforced at the level of each mode, of each term in the finite sum or at the level of the global separated form. In all cases, the sparsity prevents overfitting and allows to better capture localized behaviors.

The sparse constructors previously referred (sPGD and s2PGD) enable working at the low-data limit however, the constructor loses the benefits of orthogonal enrichments. To combine both advantages, and inspired from ANOVA analysis, one is tempted to consider the generic three-parameters approximation u(p,q,r) in the form: u(p,q,r)=f_1,p(p)+f_1,q(q)+f_1,r(r)+f_2,pq(p,q)+f_2,pr(p,r)+f_2,qr(q,r)+f_3,pqr(p,q,r), where all these terms are orthogonal. The expression can be generalized for any number of parameters. Now, by using an adequate sampling and an adequate “anchor” the previous expression provides excellent approximations, where moreover the first terms allow to evaluate sensibilities from the Sobol coefficients. Of course, the regression involved in each term can use the s2PGD to operate at the low-data limit by allying accuracy and robustness (avoiding overfitting). The different techniques are sketched in Fig. 1.

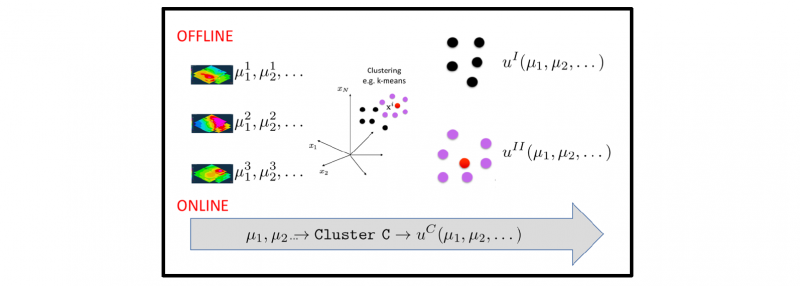
When the solution is strongly nonlinear, another alternative to enhance convergence, consists in applying a multi approximation, as illustrated in Fig. 2 [6]. For that, it suffices to cluster the high-fidelity solutions (by invoking for instance the kmeans, even if better choices exist when considering other metrics, for example topological data analysis). Now, a parametric model is constructed in each cluster. Finally, a classification is needed in order to assign any parameter’s choice to the cluster to which it belongs and, in this form, have access to the optimal parametric model.

When a parameter’s choice is in the border of two clusters, one could compute both regressions and then average them. Another procedure consists in making the approximations of the different clusters continuous by constructing a partition of unity on the basis of the mesh attached to the cluster’s centers of gravity.

Fig. 1. Non-intrusive techniques for data-approximation

Fig. 2. Multi-approximation: DoE, clustering, approximations and classification

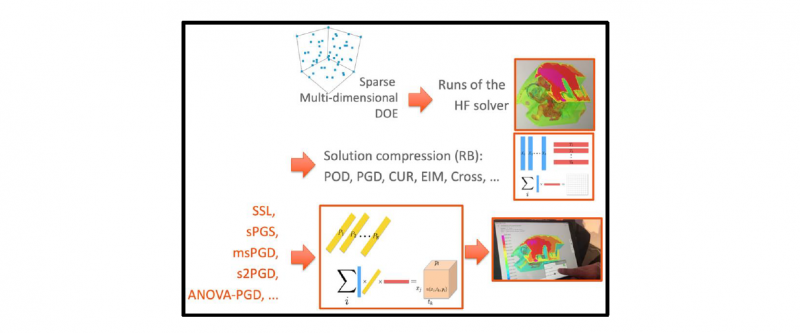
2.4 MOR Builder

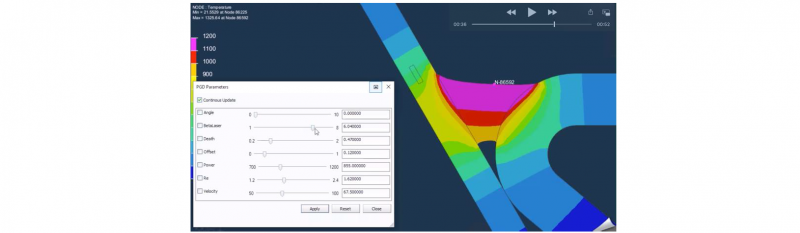
The previous technologies where inserted in a workflow that resulted in a ROM builder, sketched in Fig. 3. With respect to the previous discussion, the builder also addresses a pre-compressor to reduce the size of the files resulting from high-fidelity solvers. Thus, the high-fidelity space-time solutions can be first compressed by applying any of the available techniques: POD, PGD, CUR, Cross Approximation or Empirical Interpolation techniques (EIM and DEIM). Figure 4 illustrates a parametric solution in welding.

Fig. 3. ESI Group Platform (AdMoRe) to construct parametric solutions in a non-intrusive manner

Fig. 4. Parametric welding (SSL technique) built by the AdMoRe builder and based on Sysweld (by ESI group) high-fidelity welding solutions

3 Conclusions

In this work we revisited some of the main non-intrusive model order reduction techniques able to proceed in extremely rich multi-parametric settings, allying accuracy, frugality and robustness. Deep comparative analysis to compare the behavior of the different techniques are in progress and the results will be reported shortly. The main interests of such rich parametric solutions are multiple, in particular to perform robustness analysis in designs, and also to be incorporated into hybrid twins to make possible optimal certified real-time decision making [4].