1 Introduction
With the irruption of the so-called fourth paradigm of science, we face a new way of doing research: one in which experiments, theory, computation and data analysis—through the intensive use of machine learning—are employed simultaneously [1]. Science has been mainly experimental from its inception, nearly two millennia ago. Several centuries ago, it became theoretic, and with the help of the mathematical language, humans have been able to express beautifully the laws of the universe as universal laws. Only some decades ago, science became also computational, helped by the irruption of personal computers, but also supercomputing facilities. Finally, the last artificial intelligence summer, only some years ago, has helped scientists to extract knowledge from data. Even some attempts have been made to create artificial intelligence physicists, see [2,3].
However, machine learning techniques and, particularly artificial intelligence, behave often as a black box: there is no guarantee of the accuracy of the result and, at the same time, this result lacks most of the times of a suitable interpretation. In recent times there has been a growing interest in the development of scientific machine learning techniques able to unveil scientific laws from data. The interest is two-fold. On one hand, the possibility of leveraging big data to unveil scientific laws from them is interesting by itself. On the other, the first results suggest that the more data we add to the process, the less data we need [4,5].
In this work we review of our latest results on the development of self-learning digital and hybrid twins. In the first part, we review the development of hybrid twins based on machine learning techniques arising from a posteriori Proper Generalized Decomposition (PGD) techniques. In the second one, we focus on the development of deep learning techniques that guarantee the fulfillment of the principles of thermodynamics. Finally, we show some implementations that employ Augmented Reality to seamlessly communicate the results to the user for a fast decision making.
2 Self-learning digital twins
In our previous work, see [6,7] we develop a digital twins that is able to correct itself when the data stream do not provide with results in accordance with the model implemented in it. This is possible by resorting to the concept of sparse-PGD techniques, that finds a rank-1 tensor approximation to the discrepancy between the model and the observed results.
The developed twin, see Fig. 1, is able to provide information to the user via Augmented Reality, while locating the position of the load—and thus providing an explanation to the physics taking place—. If the results provided by the twin do not fit well with the built-in model, the twin is able to compute rank-1 corrections to the model via sparse-PGD methods.
Fig. 1. Hybrid twin for a foam beam subjected to a punctual load. The developed system is able to locate the position of the load while providing the user with useful information on hidden information such as stresses or strains [6]
In general, predictions will take the form
where A represents the built-in model, and B the self-learnt corrections. In the example in Fig. 1, the beam is modelled via a classical, linear Euler-Bernoulli-Navier beam model, which does not represent faithfully the behavior of the beam and presents systematic biases. Once these biases are detected, our technique corrects the model, as explained before, by adding as many rank-1 corrections as needed and storing them in the B-term of Eq. (1).
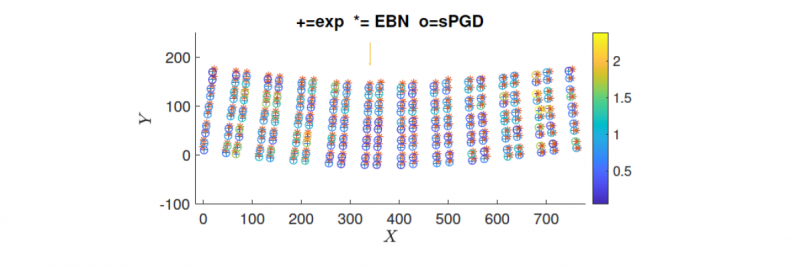
Fig. 2. Comparison between experiments (+), theoretical predictions gave by the Euler-Bernoulli-Navier model (*) and the final, corrected predictions made by the twin after the learning procedure (o). The legend represents the absolute error made in mm. Results taken from [6]
3 Thermodynamics-aware deep learning
In the last few years there has been a growing interest in the development of deep learning techniques that could take into account the accumulated scientific knowledge. This results in techniques that need for less data and whose result comply by construction with known laws of physics.
Within this rationale, the authors have developed a family of deep neural networks that are able to comply by construction with the first and second laws of thermodynamics [4,8,9,10].
Assume that the variables governing the behavior of the system at a particular level of description are stored in a vector
Under this prism, machine learning would be equivalent to finding 𝑓 by regression, provided that sufficient data is available. How this regression is accomplished is of little importance: neural networks or classical (piecewise) regression are thus equivalent, if both work well.
To guarantee the thermodynamic admissibility of the resulting approximation, we impose Eq. (1) to have a GENERIC form [4]:
Where 𝑳 represents the classical Poisson matrix of Hamiltonian mechanics (and is, therefore, skew-symmetric) and 𝑴 represents the so-called friction matrix, that must be symmetric, semi-positive definite in order to guarantee thermodynamic consistency.
In our previous works, see [2] [3], we perform regression analysis from data so as to unveil the particular form of the expression for the energy, 𝐸, and entropy, 𝑆, potentials. The resulting formulation guarantees by construction thermodynamic admissibility and provides excellent results in the data-driven identification of complex behaviors.
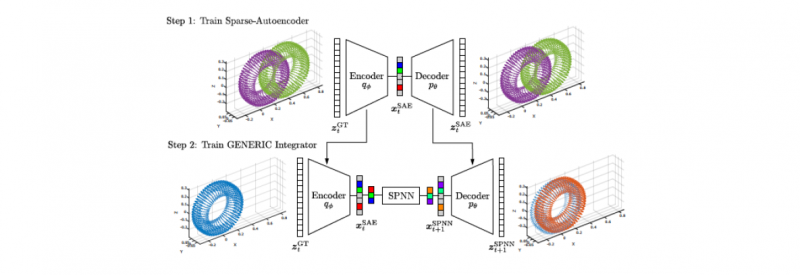
The sketch of such a network is depicted in Fig. 3. Essentially, a sparse autoencoder first determines the intrinsic dimensionality of the data set. Then, for the just determined variables-whose precise physical meaning is very often not known—a time integrator is learnt that exactly conserves energy and dissipates the right amount of entropy.
As an example, consider a Couette flow of an Oldroyd-B polymer suspension, see Fig. 4, right.
Fig. 3. Sketch of a structure-preserving neural network. In it, a sparse autoencoder first determines the intrinsic dimensionality of data. Then, a time integrator is learnt for these variables. Taken from [10]
Fig. 4. Couette flow of an Oldroyd-B polymer. Left, finite element discretization of the problem. Right, prediction done by the network for a flow whose characteristics had not been seen before: position, velocity, energy and extra-stress tensor at different positions in the flow. Taken from [10]
4 Conclusions
In this paper we review some of the developments made by the authors for the construction of hybrid twins. We have reviewed first an approach based upon machine learning of rank-1 corrections to the experimental deviations from established models of the physical asset at hand. In the second part, we have reviewed an approach based on the employ of deep learning techniques. As a salient feature, the proposed techniques guarantees by constructions the fulfillment of the first and second principles of thermodynamics.
Acknowledgements
The authors acknowledge the work done by our colleagues Beatriz Moya, Icíar Alfaro and Quercus Hernández, for their useful comments during endless discussions on the topic.
This project has been partially funded by the ESI Group through the ESI Chair at ENSAM Arts et Metiers Institute of Technology, and through the project “Simulated Reality” at the University of Zaragoza. The support of the Spanish Ministry of Economy and Competitiveness through grant number CICYT-DPI2017-85139-C2-1-R and by the Regional Government of Aragon and the European Social Fund, are also gratefully acknowledged.

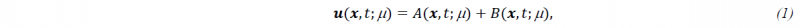
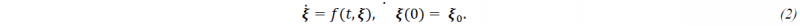
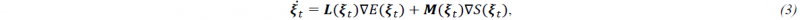
![Fig. 3. Sketch of a structure-preserving neural network. In it, a sparse autoencoder first determines the intrinsic dimensionality of data. Then, a time integrator is learnt for these variables. Taken from [10]](docannexe/image/2050/img-7-small800.png)
