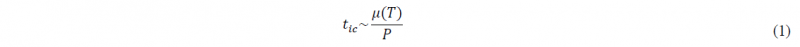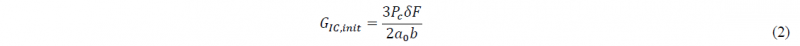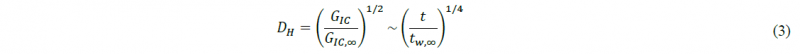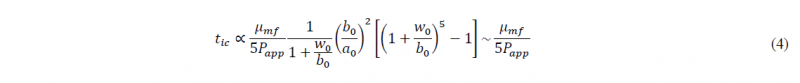1 Introduction

Thermoplastic composites have become more and more popular over the last few years mainly tanks to the ability to melt the matrix and because they require shorter processing cycles compare to thermoset composites. New forming and assembling processes have recently been developed such as overmoulding, automated tape placement, 3D-printing or welding. In all of these processes the end-quality of the part is ensured by the adhesion step between the thermoplastic pieces. Classically, the adhesion development between two thermoplastic parts requires the parts to be heated up to a temperature higher than the melting temperature of the polymeric matrix and pressed together [1,2]. The first step, where the assembly has no mechanical strength, is generally referred to the establishment of intimate contact at the interface which accounts for the initial roughness of both the adherents to explain that contact is not immediately perfect. Intimate contact at the interface has been widely studied over the last decades with the introduction of the degree of intimate contact 𝐷_ic which is equal to one for full contact. The most used model was developed by Lee and Springer [3] which simplified Dara and Loos model [4] by considering that the surface of each adherent can be modelled as a succession of identical rectangles that spread under pressure and temperature. The evolution of intimate contact is then related to the applied pressure, the viscosity, the temperature and the geometry of the rectangles. These models were then developed to improve the description of the roughness of each adherent, Yang and Pitchumani [5], for example, described the surface using a fractal cantor set and a squeeze flow model to predict their spreading during the process. All of these models make use of a characteristic time for intimate contact establishment t_ic:

where 𝜇(𝑇) is the effective temperature-dependent viscosity of the composite blend and 𝑃 is the closing pressure.

Levy et al. [6] proposed a relation between the 𝐷_ic and the internal thermal contact resistance between the layers during consolidation of a PEEK-carbon laminate.

Once intimate contact is completed at the interface, the macromolecular polymeric chains are free to move across the interface. This is the healing step where the mechanical resistance of the assembly progressively builds up to the one of the bulk [7,8]. This process is based on de Gennes reptation theory [9] where full healing is achieved after a time greater than the reptation time t_rep. In the case of long macromolecules, the authors considered that healing can be completed after a lower time, the welding time t_w [1,10].

Today, manufacturing processes tend to be faster and faster, if not continuous, limiting consequently the time require to develop both intimate contact at the interface and healing. Yet, these adhesion theories have mainly been validated experimentally for long residence time ranging from a few minutes to a few days. It is therefore very relevant to characterize the bonding between coupons for short residence time to understand, control and predict these fast processes.

This paper first aims at characterizing the development of adhesion for short residence time obtained at different isothermal welding temperature. Moreover, to our knowledge, there is only a few studies that investigate the role of contact pressure on the adhesion development [11] during welding processes, especially for those short residence duration. Thus, the effect of contact pressure was concurrently studied and empirical identification of intimate contact time establishment is proposed which could then be compared to the already well-established models.

2 Materials and experimental methods

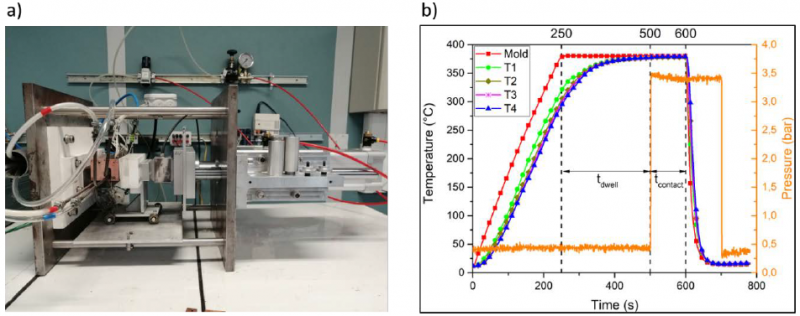
The material used in this study is a high performance PEKK-carbon thermoplastic composite. It consists in a 12 symmetric unidirectional [0°/90°] plies layup. One of the surface of the coupon is enriched with a 50 μm layer of neat PEKK 7002 layer which will ease the welding process afterwards. The whole layup was consolidated in an autoclave at high temperatures under 5 bars. The 2.3 mm thick autoclaved composite plates were then cut into 125 x 25 mm samples using water-jet cutting and dried under vacuum at 180°C for at least 20 hours. The coupons are welded together using an experimental welding bench (TACOMA) [12] in isothermal conditions at high temperatures such as the polymeric matrix of the composite was in the molten state. The contact pressure was applied once the temperature was homogeneous at the interface of the samples which were not in contact at the moment. After a certain contact time, the welding procedure was quickly stopped thanks to water circulation in the welding bench. Both the experimental setup and the welding procedure are shown in Fig. 1. Three isothermal temperatures were first studied: 380°C, 370°C and 355°C. The pressure effects on the adhesion development was investigated at a temperature of 355°C under different contact pressures: 5, 3.2, 2.5 and 1.5 bars. The contact time for all experiments ranged from one second to a few minutes. After welding experiments, the adhesion energy of the assembly was quantified using a Double Cantilever Beam (DCB) fracture tests according to the ASTM standard recommendations in quasi-static conditions at an imposed displacement rate of 1mm.min-1. Prior to welding, a 20 μm aluminum foil was inserted between the samples to initiate the crack during the DCB test. The mode I interlaminar fracture toughness was then calculated at the initiation point of the crack according to Eq. (2):

where 𝑃_𝑐 is the critical force required to initiate the crack, 𝛿 is the corresponding displacement, 𝑎₀ is the initial crack length which is equal to the length of the inserted aluminum foil and 𝑏 is the width of the coupons. 𝐹 is a correction factor according for large displacements effects.

Fig. 1. (a) The TACOMA experimental welding setup and (b) the welding procedure.

3 Results and discussion

3.1 Temperature Effects

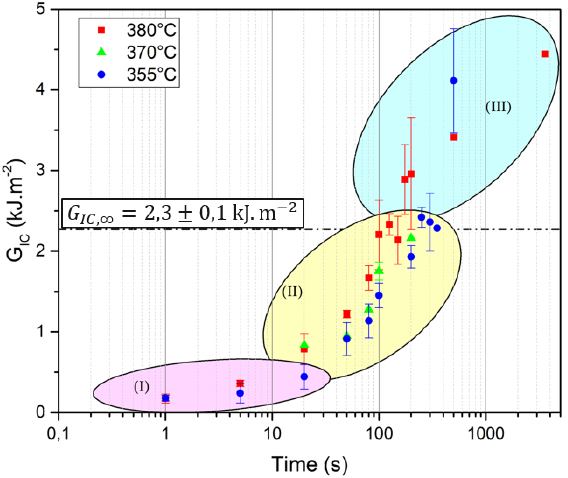
Welding experiments were performed for three isothermal temperatures using the protocol presented in Fig. 1(b). The results are presented in Fig. 2. Three adhesion regimes have been identified [12]: The first one (I), at the shortest contact times, is a coupled regime where intimate contact is not fully achieved and healing has already started at some spots. The second regime (II) is a healing regime where the interlaminar fracture toughness increases linearly with the square root of contact time which is only due to autohesion of the polymer at the interface. Finally, in the terminal regime (III), other adhesion phenomena like fiber bridging occur which induce higher values of G_IC which are thus not associated to pure healing. Healing kinetics was already previously identified in [12] from the analysis of the second regime and won’t be analyzed in this paper. Conversely, in the next section, we will investigate in details the first regime and more precisely the establishment of intimate contact at the interface.

Fig. 2. Evolution of interlaminar fracture toughness for three isothermal temperatures versus contact time. Highlight of the three identified bonding regimes

3.2 Pressure Effects

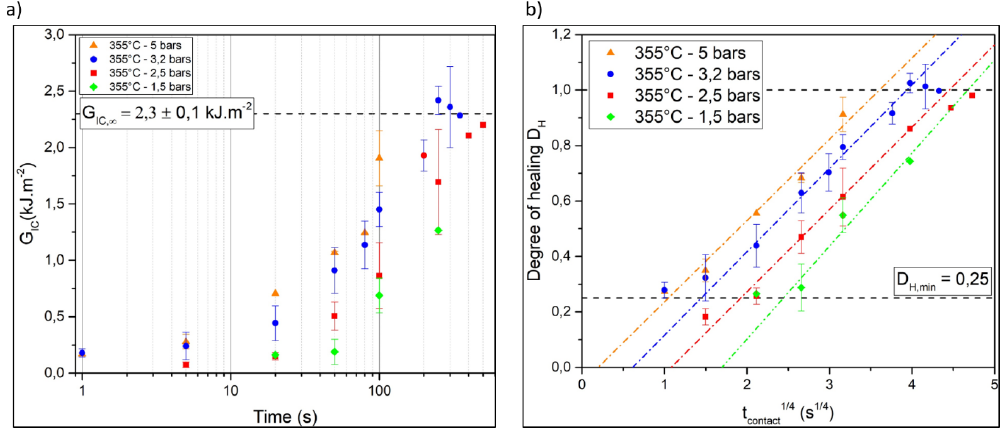
The evolution of interlaminar fracture toughness for different contact pressures at 355°C is shown in Fig. 3(a). The first bonding regime, where establishment of intimate contact develops, is strongly slowed down when the contact pressure decreases. This corresponds to a delay in the beginning of the healing step. As a consequence, for high pressure, the healing step may be the limiting phenomenon for adhesion development whereas for low contact pressure, the limiting step would then be the establishment of intimate contact. On the other hand, the degree of healing can be calculated (Eq.(3)) and plotted against the fourth root of time for these different contact pressures. Following the previous procedure detailed in [12], the welding time is given from the slope of a linear fit of the second bonding regime, corresponding to the healing kinetics in Fig. 3(b). This procedure was applied for the different contact pressure expected for 1.5 bar for which the data were not sufficient to have a consolidated value of t_w,∞. The identified welding times are then reported in Table 1 for the different contact pressures and it can be seen that there is a slight increase of the welding times with the decrease of the contact pressure. This evolution could probably be insignificant considering the scattering of the results.

Fig. 3. (a) Evolution of the mode I interlaminar fracture toughness versus contact time for different contact pressure at 355°C and (b) the corresponding healing degree. The linear fit correspond to the identification of the healing kinetics.

Table 1. Identified welding times corresponding to the healing step for the different contact pressure

From the evolution of the healing degree versus the fourth root of time (Fig. 4) one can see that the initial value of D_H seems to be constant for the very short residence times corresponding to the slowdown in the establishment of contact. This value is then referred as D_H,min and could be related to either the initial degree of intimate contact D_ic(t=0) or the adhesion development during the cooling phase of the procedure. Indeed, though the characteristic cooling rate at the welded joint is fairly rapid, of about 12°C/s [12], adhesion could still develop between the molten state and the glass transition temperature or crystallization which will not be study here. Here, since we observe that D_H,min seem to be constant for longer time as the pressure decreases, we can consider that this value is mainly controlled by the initial value of the intimate contact degree D_ic(t=0) which therefore seems to be quite homogeneous all over the samples tested. The lower the pressure, the longer it takes for the interface to complete the contact and since this initial value does not vary much, we can suppose that the amount of healing occurring during the first regime is negligible compared to the intimate contact development. Finally, this minimal value of D_H corresponds to the limit of the possible measurements using this experimental procedure. Indeed, for the very short residence times and the very low pressures, the mechanical bond is so weak (due to the low amount of healing for these first values) that the assembly often broke either at the opening of the mold or in the first moments during the double cantilever beam test. As a consequence, for residence time lower than 1 second, no healing has occurred and thus the assembly present no mechanical resistance and the measurement of adhesion energy is impossible. The value of D_H,min was determined from the average of the first values of D_H for each contact pressure and was found to be equal to D_H,min = 0,25.

From this, since intimate contact is fully established when the healing phase starts, the intersection between the linear fit corresponding to the healing stage and D_H,min could then approximate t_ic, the time required for a perfect contact between the adherents. This time is not precisely the intimate contact time as defined in the literature since the first adhesion regime is a coupled regime between intimate contact and healing, thus at the identified time, healing as already started but to a lower extend than intimate contact. This time is thus only a characteristic time that can approximate the intimate contact time and will still be referred as t_ic. In particular, it follows the same trend as the intimate contact time. This approximated intimate contact time is finally plotted versus the applied contact pressure in Fig. 4. The Lee and Springer model [3] gives the following expression (Eq.(4)) for the time required for a complete intimate contact which depends on the geometry of the asperities, the viscosity of the composite blend μmf and the applied pressure P_app:

The best fit of the experimental values of t_ic as proportional to 𝜇_mf / 𝑃_app is then showed in Fig. 4.

This dependency proposed by Lee and Springer [3] does not predict correctly the evolution of intimate contact time with the contact pressure for this material. The establishment of intimate contact at the interface predicted by the Lee and Springer model [3] seem to be much slower than the experimental data presented in this study. Overall, the evolution of experimental t_ic with contact pressure validates that intimate contact is strongly slowed down when the pressure decreases. One can also see that a minimal pressure should be apply to initiate the contact before healing which is particularly the case for the welding of composite materials due to the presence of fibers. On the contrary, for a neat polymer, it is expected that intimate contact would be instantaneously achieved only due to the low viscosity at high temperatures.

As a perspective, a phenomenological model could be proposed from the experimental identification of t_ic which is based on the mechanical characterization of the welded joints without the need to determine the geometry of the initial asperities. Indeed, from a practical point of view, it is very challenging to measure the dimensions of the rectangles used in the existing models. The proposed identification, though purely phenomenological, could thus be an alternative to these models and could be applied to simulation of asperities squeezing for validation and comparison. One can however already say that this measured experimental trend is far much faster that the classical one predicted by Lee and Springer's approach [3] and widely used in the literature.

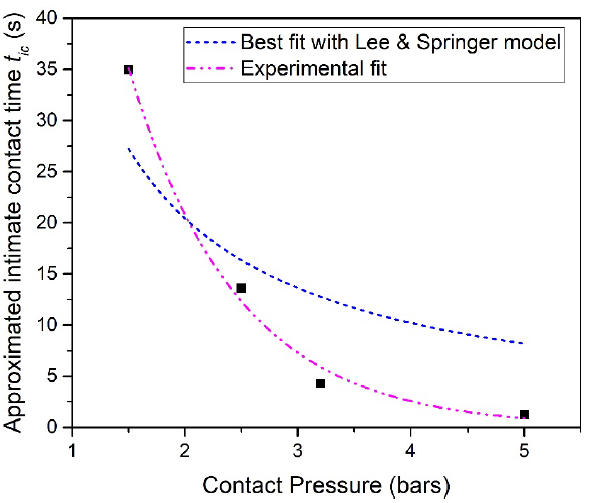Fig. 4. Evolution of the identified intimate contact time t_ic in function of the applied contact pressure for a temperature of 355°C.

4 Conclusions

In this work adhesion of high performance thermoplastic composite is studied using an experimental welding bench for short residence time. Study for three isothermal welding temperatures provide basis for the analysis of the two phenomena that takes place during adhesion performance: intimate contact at the interface and healing of the interface with the identification of the three bonding regimes. Then, welding tests performed at different contact pressure provide more specific insights on what could be the limiting phenomena for adhesion development. A constant minimum value of adhesion has been related to the initial intimate contact degree. Then, an empirical identification of an approximated intimate contact time t_ic for perfect contact at the interface is proposed. This was compared with the most used intimate contact model which was shown to not accurately predict the evolution of time required for full intimate contact which seems to be much slower that the experimental data presented.

Time for perfect contact was shown to exponentially increase with the decrease of the contact pressure. It was then explained that for a composite material, a minimal contact pressure is required to initiate the establishment of intimate contact which shouldn’t be the case for a neat polymer. The higher the pressure, the shorter is the completion of intimate contact.

The experimental proposed method is a phenomenological identification of this intimate contact and makes no use of the geometry of the initial asperities unlike the existing models and is solely based on the mechanical characterization of the welded joint. Thus, as a perspective for future research, a phenomenological model will be developed to predict the establishment of intimate contact at the interface which will allow the modelling of the whole adhesion process for this high performance thermoplastic composite.

Acknowledgements

The authors would like to thank Jérôme Delmas and Nicolas Lefevre for their help on the designing and machining of the welding setup. The authors also acknowledge the funding of the PERFORM project managed by the IRT Jules Verne (French Institute for Research and Technology in Advanced Manufacturing for Composite, Metallic and Hybrid Structures) that made this work possible. The authors wish to associate the industrial partners of the PERFORM project: Airbus, Stelia Aerospace, Faurecia, Naval Group and Daher.