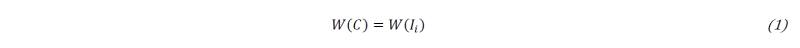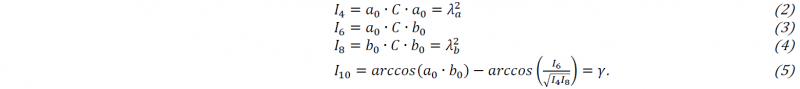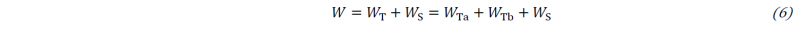1 Introduction

In recent years, sustainability and climate protection have become key issues. This is also apparent in the design process of lightweight structures. Modern lightweight constructions are realized in a multi-material design. Therefore, joining or combining materials of different material classes has become a significant part of the development process. A special type of multi material design are fiber-metal laminates (FML), which combine the advantageous properties of metals and fiber reinforced composites in a layer-wise material. However, this makes the manufacturing of parts from this material an enormous challenge. Classical FMLs, like GLARE, were developed for the aviation industry and are expensive in their production [1]. For mass production of FML parts, the costs of material and process have to be decreased and the producible complexity of the parts has to be increased.

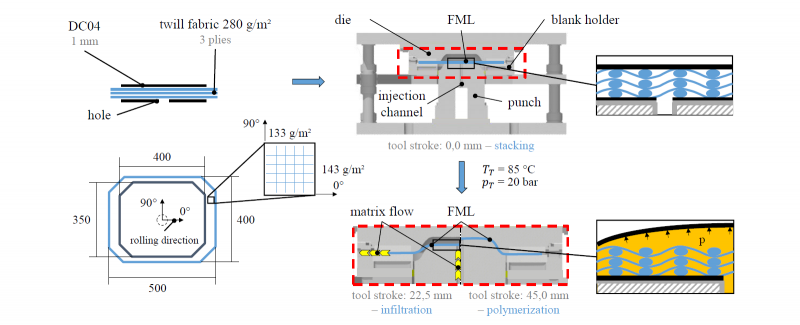
One possible process could be the combination of deep drawing and thermoplastic resin transfer molding (T-RTM) [2]. The deep drawing of the metal sheet, the draping and the infiltration of the fabric are performed simultaneously in this one-step process (Fig. 1). In previous work, the authors presented a finite element (FE) model and a parametric study to simulate this process [3, 4]. They have shown that the common known compressive stresses in deep drawing processes require an in-plane compression sensitive membrane modelling of the fabric. Without accounting this in-plane compression sensitive fabric behavior, unrealistic deformation modes occur, like shear bands. At first, this paper summarizes the membrane behavior of fabrics and then it reviews mechanical macroscopic models for fabrics. Finally, conclusions are drawn for a new fabric material model, which can account for in-plane compressive stresses and full membrane coupling.

Fig. 1. Process flow of combined deep drawing and resin transfer molding

2 Mechanical behavior of woven fabrics

A woven fabric is a plane textile structure produced by the technique of weaving. The consideration and modelling of woven fabrics can be done on three scales. On the microscale, several thousand individual fibers form a fiber bundle. These bundles are called threads or rovings and are assumed to be homogeneous at the meso-level. The most common form of fabrics are two-dimensional fabrics consisting of interwoven fiber bundles in two directions. At the macroscale, individual rovings are not considered, but the fabric is assumed to be a homogeneous solid instead [5]. Rovings in the direction of production are referred to as warp yarns (here 0° or a), while those running perpendicular to them are referred to as weft yarns (here 90° or b). The waviness of the rovings that results from the weaving is called crimp. Despite the resulting three-dimensional structure, this type of weave provides only in-plane reinforcement and is therefore referred to as two-dimensional [6]. The proportions of straight and curved roving sections change with the weave type, thereby influencing the achievable fiber volume fraction and the macroscopic material behavior significantly [7, 9].

Due to the structure of fabrics, their macroscopic material behavior differs from that of continuous solids. The fiber directions cause a strong anisotropy of the material. Boisse et al. [10] have shown that macroscopic nonlinear behavior is essentially attributable to geometry changes at the meso-level and depends only to a small extent on nonlinearities in the contact points. The crimped and interacting rovings also cause the material behavior under tensile loading to differ from that under compressive loading. This tension-compression anisotropy has hardly been explored so far.

2.1 Tension behavior

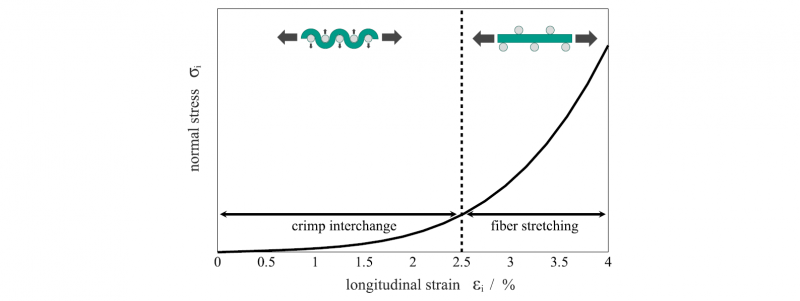
Some working groups are dedicated to the computational determination of the effective stiffness taking into account the fabric architecture. Starting from a geometric model at the meso-level, material properties depending on the local fiber orientation and fiber volume fraction are assigned to the constituents (fiber, matrix and interface). Then, using classical laminate theory (CLT), the effective macro-level material properties are determined [6, 11]. Instead of using CLT, the properties can also be determined using the "theory of effective moduli" [9]. Other studies differ mainly in their assumptions on the cross-sectional geometry of the fibers. Dixit and Mali [7] give a detailed overview of the different approaches to predict the mechanical properties, especially the tensile stiffness. However, none of these analytical approaches takes into account the actual processes during deformation. For a better understanding of the fabric material behavior under tensile loading, it is important to analyze the processes at the meso-level, since here the behavior is mainly determined by geometric changes. In their work, Kashani et al. [12] describe the macroscale behavior due to mesoscale processes in plain weave fabrics under different loads. Based on experimental data, different coupling mechanisms and influences can be inferred. Due to the interwoven structure of the rovings, interactions occur between them. Strain in one fiber direction consequently induces not only longitudinal normal stresses but also stresses in the transverse direction. This biaxial behavior leads to an effect corresponding to transverse contraction in homogeneous solids. This is evidenced by experimental results of biaxial tensile tests on fabrics with different strain ratios between the two roving directions [10]. The uniaxial stress-strain curve without transverse pre-tensioning can be divided into two regions, as shown in Fig. 2. Both regions are attributed to different physical phenomena.

Fig. 2. Characteristic tensile stress-strain diagram of a fabric according to Kashani et al. [12]

First, under tensile loading, the crimping in the rovings is reduced along the tensile direction. The reduction of crimping in one direction causes increased waviness of the transverse yarns. This effect is often referred to as "crimp interchange". Under uniaxial tensile loading without hindrance to transverse contraction, this change in crimping can easily occur. The slightly ascending uniaxial tension curve at small strains describes this smoothing mechanism. After the reduction of crimping in the rovings along the tensile direction, they are stretched as the load increases. Due to the high tensile stiffness of the fibers, there is a sharp increase in tensile stresses with increasing strain. Transverse pre-strain makes crimp interchange more difficult and thus increases the energy required to achieve a given longitudinal strain. In the stress-strain diagram, this is noticeable by a steeper progression in the smoothing zone. In the region of large longitudinal strains (ε_i > 3 %), experimental studies show a more compliant behavior for fabrics with increasing transverse pre-tensioning. One explanation for this could be that with increasing transverse pre-stretch, the crimping in the rovings is reduced to a lesser extent along the tensile direction, resulting in a more compliant strain behavior [12]. Since large displacements in fabric forming are realized mainly by large shear deformations, only the range of small longitudinal strains is often considered [5, 13].

In further experimental investigations, the influence of the current shear deformation on the tensile behavior was analyzed. Compared to the influence of transverse strains, the effects of shear deformation on normal stresses are very small. Accordingly, the biaxial coupling has the largest influence on the tensile behavior and should therefore be considered in a material model for draping simulations [12].

2.2 Compression behavior

There have been no published studies on the material behavior of fabrics under in-plane compressive loading. Various publications report that the compressive stiffness is very low compared to the tensile stiffness, which is why it is assumed to be almost zero in many numerical calculations [14, 15, 16, 17, 18].

2.3 Shear behavior

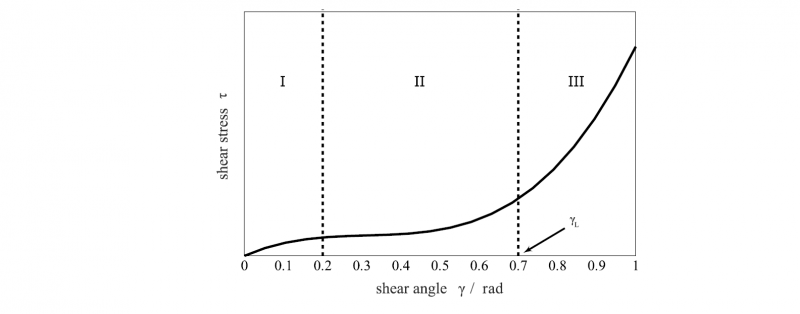
Shear deformation is the central deformation mechanism in fabrics, especially in doubly curved structures [19]. Idealized, the contact points of warp and weft rovings act as hinge points allowing only in-plane rotations, justifying the assumption of pure shear. The shear angle γ describes the angular change between the two roving directions. Fig. 3 shows the characteristic shear stress curve without the influence of normal strains along the fiber directions. It can be divided into three zones.

Fig. 3. Characteristic shear stress – shear angle diagram according to Launay et al. [20]

In the first zone (I), pure rigid-body rotations of the rovings take place. The low shear force can be attributed solely to the friction in the contact points. As soon as the rovings come into lateral contact with each other, an increase in force follows, which is visible in zone II. The higher force can be explained by the lateral compaction of the rovings. The transition between zones II and III is marked by the critical shear angle γ_L, which is often also referred to as the shear-locking angle. The state of maximum compaction is called shear-locking and is characteristic for the third region (III). Further shear deformation is possible only under large force application. In addition, high compressive stresses occur across the fibers, which often leads to wrinkling due to the low bending stiffness of fabrics [20, 21]. Characterizing the shear behavior of fabrics using analytical models is difficult, so complex meso-level simulations [22] or experimental studies [19, 20, 23] are mainly used. The paper published by Cao et al. [23] contains benchmark tests of various research groups characterizing the shear behavior using picture frame (PF) and bias extension test (BET). They explain the necessity to use normalization methods to compensate the influence of different test setups on the results. Among other things, preconditioning is suggested, because the fabric shows a stiffer behavior during the first deformation cycle compared to further cycles. For the description of industrial applications, the behavior in the first cycle is decisive, since the forming processes occur without preconditioning [23].

No information is currently available on the shear behavior under compressive loading along the fiber directions, so further investigations are necessary for this area. Therefore, only the influences of positive normal strains are described in the following. Similar to the tensile behavior, the shear behavior shows strain-dependence. In their work, Nosrat-Nezami et al. [19] demonstrate that an increase in membrane strains increases the shear stiffness of carbon fiber fabrics. In the shear stress diagram, this effect is shown by a steeper curve as well as a sharp initial increase of shear stress. This initial jump can be attributed to the fact that for strains in the fiber direction, the rovings interact more strongly with the transversely extending rovings. The resulting larger contact forces at the crossing points of the rovings increase the friction between warp and weft yarns, thus complicating the rotations, which dominate the behavior in the range of small shear angles. Biaxial pre-stretching of the fabric maximizes this effect. For very large shear angles in the range of the shear-locking angle, the influence of the normal strains decreases [12, 20]. Thus, the coupling is nonlinear, and the actual coupling behavior depends on the fabric structure. For draping simulations, the range of small and medium shear angles is of particular interest. Furthermore, globally applied strains along the rovings increase the resistance to wrinkling, whereas local strains facilitate wrinkling [19]. The influence of normal strains on the shear behavior is particularly important in manufacturing processes that operate with high forming and blank holder forces [20]. The dependence of the shear behavior on the normal strains is called the tension-shear coupling and is the strongest coupling in the deformation behavior of fabrics. Its influence even exceeds that of biaxial coupling, so that consideration of tension-shear coupling in material models is necessary [12].

2.4 Bending behavior

The bending behavior of fabrics influences the formation and shape of wrinkles during forming. If fiber structures, such as woven fabrics, are subjected to a bending load, relative displacements occur between the individual, tensile-stiff fibers. Accordingly, the bending behavior of a fabric differs significantly from that of a continuous solid. Fiber sliding leads to a comparatively lower bending stiffness, so that severe bending is possible without fiber damage [24]. Boisse et al. [25] have shown that classical plate or shell theories, which establish a relationship between tensile and bending stiffness, cannot realistically describe the bending behavior of fabrics. In order to provide an acceptable representation of bending behavior in numerical models, bending and membrane behavior are usually modeled independently [7, 8]. For this reason, the bending behavior is not taken into account in the further consideration of this work.

3 Review on mechanical macro-models for woven fabrics

In macro-models, individual rovings are not represented and the entire fabric is considered as a continuum. This requires a lower computational effort compared to mesoscopic models and thus allows the numerical calculation of larger models. The geometric effects on the mesoscopic level described in Section 2 are not reproduced on the macro-level. For this reason, the nonlinear macroscopic material behavior must be embedded in the constitutive equations. For this purpose, two approaches are mainly followed in the literature.

3.1 Cauchy-elastic material models

The first approach is based on the definition of Cauchy-elastic material properties along the material directions in the covariant reference frame. The Cauchy-stresses are coupled directly with the strains. Since fabrics can undergo large shear deformations during forming, it follows that a non-orthogonal constitutive model is needed [16]. The core of the work by Xue et al. [16] is the decoupled description of tensile and shear properties in the covariant coordinate system along the fiber directions. The material properties are first represented as parameters in the constitutive equations. It is also assumed that the material is incompressible. Using transformation matrices, the material equations are transformed into the initial orthogonal reference frame. FE simulations are then performed with the model, and the material parameters are determined via comparison with experimental studies. With this model, the representation of nonlinear behavior is possible, but coupling mechanisms are not considered. Peng and Cao [14] use an alternative representation of stresses and strains under unchanged assumptions. Furthermore, they implement a method to track fiber directions to guarantee alignment of material behavior along them. In further work by Lee et al. [22], the model is extended individually to include membrane strain-dependent shear behavior and biaxial tensile behavior, respectively. The parameters describing these couplings are determined from simulation results of mesoscopic models. Subsequently, the material model is applied in FE simulations at the macro-level and compared with experimental data [27, 28].

The FABRIC model available in ABAQUS also uses the Cauchy-elastic approach. Experimental data on uniaxial tensile behavior and shear behavior must be passed as input variables. Alternatively, the material properties can be provided via a subroutine. With the help of an algorithm that tracks the fiber directions, the material properties are always aligned along the rovings. It is possible to specify different data for loading and unloading. A consideration of couplings is not provided, but could be implemented via the subroutine VFABRIC [29].

3.2 Hyperelastic material models

The second frequently used approach is based on hyperelastic material modeling. The most important component of hyperelastic material models is the formulation of a potential function from which a stress measure can be calculated by derivation with respect to a kinematic quantity. In some cases, this type of modeling allows to set up the material equations with respect to the initial configuration, so that no complex coordinate transformations have to be performed. All here presented models use the strain energy density W as potential function and formulate it according to

as a function of the invariants of the right Cauchy-Green tensor C (RCG) in combination with the initial fiber directions a₀, b₀. The invariants are described by

Here, the invariants I₄ and I₈ represent the quadratic stretch 𝜆_i² (i = a, b) of one roving direction and I₁₀ is the shear angle between the roving directions in accordance to the initial orientation. It is also assumed that the total strain energy density W can be decomposed additively into a tension-compression dependent component for each fiber direction W_Ti and a shear component W_S according to

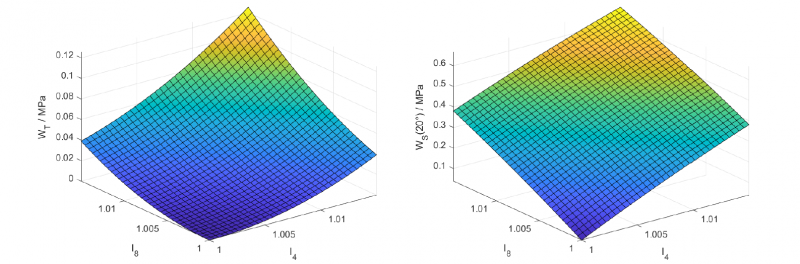
as shown in Fig. 4. Forming the derivative of the strain energy density according to the RCG tensor yields the second Piola-Kirchhoff stresses. It is also assumed that there is no energy dissipation due to friction. The first hyperelastic material models consider neither the in-plane compression strains, nor coupling mechanisms. In each case, the tensile-dependent components of the distortion energy density depend only on the elongation in the fiber direction, and the shear-dependent component is determined by an invariant associated with the shear angle. The parameters of the individual components are determined by means of uniaxial tensile tests and picture frame tests [17, 30, 31]. Based on these publications, further work has extended the model to include the influence of viscous matrix [15, 32], the biaxial coupling of the tensile-dependent components [33, 34, 35], and the tension-shear coupling [18, 32, 36]. Depending on the considered coupling, uni- and biaxial tensile tests as well as picture frame tests with and without membrane strains are necessary to determine the parameters. The models already show good agreement with experimental data, even for complex geometries. Model quality increases with the representation of coupling mechanisms.

Fig. 4. Energy density functions W_T and W_S for biaxial coupling with positive elongation according to Yao et al. [33 - 36] calculated with data from Komeili et al. [5]

3.3 Other approaches

Galliot and Luchsinger [37] propose another macroscale material model. It is based on an orthotropic modeling approach fitted via experimentally obtained data. The material model focuses on the biaxial coupling under tension loading while the complex shear behavior is not represented. Boisse et al. [38] use a newly developed shell element for FE simulations in various publications [10, 21, 39, 40]. The element takes into account the biaxial tensile behavior, but the influence of the membrane strains on the shear behavior is not shown [21, 40]. Another work follows a semi discrete approach, where a finite element consists of a certain number of unit cells. This approach ranks between the meso- and macro-levels [39]. In addition, Iwata et al. [41] propose a combined approach of a meso- and a macro-model in their work. They refine a macro-level numerical model with local numerical calculations at the meso-level.

A publication that represents both, the transverse strain-dependent tension behavior and the membrane strain-dependent shear behavior, is not yet known. Moreover, the deformation behavior under combined in-plane compression has not been considered yet in macroscopic material modeling.

4 Conclusions and research demands for macroscopic modeling of fabrics with in-plane compression and full membrane coupling

The combined deep drawing and T-RTM process requires high blank holder forces for forming of the stiff metal sheets. Without these, the metal sheet would buckle. This induces combined stress states with in-plane compression stresses in the intermediate fabric layers. To model this complex multiaxial deformation behavior, a material model is needed, which considers the tension-compression anisotropy, the biaxial coupling resulting from crimp interchange of the rovings and the shear stiffening or softening due to membrane tensile or compressive strains. A conceivable approach would be a hyperelastic, invariant-based modelling approach, e.g., based on the work of Yao et al. [33, 34, 35, 36]. However, the equations contributing to the strain energy density have to be extended to negative strains. Furthermore, the equations have to be modified to fit the more complex behavior, where care has to be taken on the mathematical continuity in case of a piecewise description of the material behavior. Depending on the level of the material equations (stiffness level, stress-strain level or energy level), multiple continuously differentiable functions are necessary. Based on these findings, the authors intend to develop such a model in future work and implement a corresponding material subroutine in Abaqus/Explicit.

Acknowledgements

The German Research Foundation (DFG) kindly supports this research project (HE 6154/4-1, HE 6154/4-2). Moreover, the authors thank their colleagues for support, especially Constantin Krauß and Christian Poppe.