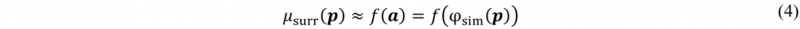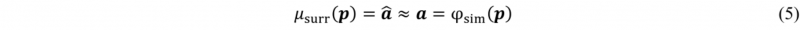1 Introduction

Optimum operation of production lines in terms of part quality, cycle time or cost generally requires diligent parameterisation of manufacturing processes. In practice, identification of such optimum parameters during production ramp-up usually involves many time and resource-intensive experimental trials and experiential expert judgment. Thus, an entirely experimental optimisation rapidly becomes cumbersome. This holds all the more for complex processes and delicate materials, e.g. such as technical textiles used in fibre-reinforced components.

High-fidelity process models, e.g. finite element (FE) simulations, offer means for virtual process analysis. In combination with general-purpose optimisation algorithms, e.g. evolutionary algorithms [1], they provide options to systematically and reliably optimise manufacturing. Often termed “virtual process optimisation”, such approaches may help determine promising parameters prior to actual experimental trials. Despite significant process improvements being reported, e.g. [2], reliable models typically require considerable computation times of e.g. hours and days. Iterative optimisation then becomes time-consuming and, in many cases, impracticable. Consequently, time-efficiency is a key factor during optimisation.

One option to reduce the overall computational load is surrogate-based optimisation (SBO). SBO employs numerically efficient approximations of the high-fidelity process model, the “surrogate”, which guide the optimiser in the parameter space [3]. In material forming, as considered in this work, most SBO-applications focus on metal forming, e.g. [4]-[6]. Recent work of the authors additionally addresses textile forming [7],[8]. All studies report a significant speed-up of optimisation.

Although simulations typically provide detailed process information, most surrogate techniques of prior work consider scalar or low-dimensional product attributes only. This „compression“ or „truncation“ of data limits the amount of usable information gained from simulations. Advanced Machine Learning (ML) techniques, e.g. deep learning (DL), enable novel surrogate types, which do not merely reflect an abstract performance scalar but consider full-field simulation data [7]-[11]. According studies report high surrogate accuracy and thus tacitly expect improved optimisation performance, yet fall short on quantitative comparison: To the authors’ knowledge, to date no benchmark against classical, scalar surrogate techniques is available and only [7] gives a brief glimpse on SBO with DL-models. This work aims to substantiate and enhance current findings with numerical evidence regarding optimisation performance.

The scope of this study is twofold: first, predictive accuracy of DL-surrogates is compared to classical surrogates (full-field vs.scalar surrogates) for different number of training samples. Full-field prediction is achieved with a deep neural network (DNN). It predicts the entire strain field with n_el = 22080 elements during textile forming. Second, four different SBO-strategies give insight into optimisation performance and the observed convergence is benchmarked against a state-of-the-art evolutionary algorithm (EA).

2 Workflow and Use-case

Due to their superior mechanical properties, continuous-fibre reinforced plastics (CoFRP) have drawn increasing attention in weight-sensitive industries. However, they typically invoke higher cost, not least due to higher engineering effort for defect-free production. Manufacturing of CoFRP-components typically comprises multiple steps, often including a forming step of an initially flat textile (“draping“), e.g. woven fabrics as considered in this work.

Woven fabrics show a comparably low shear stiffness compared to tensile stiffness in warp or weft direction. This makes in- plane shear the predominant deformation mechanism, which is quantified by the in-plane shear angle γ₁₂ (Fig. 1 a). For brevity, this work uses γ=γ₁₂ . Alike any other material, woven fabrics show a material-dependent forming limit, which is usuallyquantified by the locking-angle γ_lock . Excessive shear beyond γ_lock increases the likelihood of unwanted defects, such as wrinkling or poor permeability during subsequent resin infiltration (“dry spots”). Therefore, γ is often minimised in process optimisation.

2.1 Simulation Model for Optimisation

This work studies forming of the double-dome geometry, a common benchmark geometry in textile forming. Regarding forming simulation, a macroscopic FE-based modelling approach is applied. It employs constitutive descriptions of the relevant deformation mechanisms by subroutines within the FE-solver ABAQUS/EXPLICIT. See [12]-[14] for modelling and parameterisation details. Superposition of membrane and shell elements ensures decoupling of membrane and bending behaviour and a non-linear shear modulus captures material-specific shear locking. Discrete rigid surfaces model the tool surfaces and the tool closes within t_tool=2 s in a single stroke. Fig. 1 b) shows an example simulation setup along with an according forming result (shear angles).

Fig. 1. Visualisation of shear angle and example of textile wrinkling [2] a), forming simulation setup and an example forming result (top view on shear angle distribution) b).

Process manipulation is possible through 60 grippers modelled by springs (0.01N/mm ≤ c_i ≤ 1 N/mm). They are uniformly distributed around a rectangular blank of thickness s=0.3 mm, cf. Fig. 1 b). Similar to conventional blank holders, they introduce tensile membrane forces into the textile which restrain material draw-in during tool closure. An in-house-developed pre- and postprocessing framework allows for fully-automatic model generation and result analysis during optimisation. Despite symmetry of geometry and material, no symmetry conditions are applied, since – in principle – springs may become asymmetric during optimisation.

2.2 Surrogate Approach

In general, a process simulation may be seen as a function φ _sim : P ↦ A which maps process parameters p∈P to a part quality attribute a∈A. In many cases, A quantifies part quality by extent of defects, e.g. formation of wrinkles or cracks. This work considers γ as a proxy to wrinkling as outlined above. Please note, that 𝛾 is an elemental quantity and thus the overall product quality a=γ=(γ¹,...,γ^nel)^T is a vector in ℝ^nel with n_el being the count of fabric element. Analogously, the circumferential spring stiffnesses represent the variable process parameter search space, i.e. p=c=(c₁ ,...,c₆₀)^T.

Ultimately, an objective function 𝑓:A ↦ Q must map the part quality attributes to a scalar performance metric q ∈ Q ⊂ ℝ. Virtual process optimisation then amounts to finding

However, evaluating φ_sim is often so costly that a direct optimisation using iterative algorithms takes prohibitively long. For increased efficiency, surrogate-based optimisation (SBO) proposes devising an easy-to-evaluate approximation μ_surr:P ↦ Q with

In general, φ_sim is a „black-box“-function, i.e. it can be evaluated but it otherwise unknown. In such cases data-driven proximations based on n input-output-observations 𝐷ⁿ={(p₁, f(a₁)),...(p_n, f(a_n))} are suitable. For this, a plethora of different techniques exists [15], e.g. polynomial regression, Support-Vector techniques or Neural Networks. Differences in model function aside, they a all follow the notion of tuning model parameters θ ∈ Θ towards minimisation of an error metric 𝜀_err, e.g. mean squared error (MSE)

, which is also used in this work.

This work concentrates on deep neural networks (DNN) since they pose several advantages: first, they are universal approximators [16]. That is, given sufficient data they can reproduce any continuous function irrespective of its complexity and thus promise general suitability as surrogates. Additionally, over the last decades a large community of researchers developed specialised sub-types of DNNs for specific tasks (image-recognition, time-series-analysis,…) and embodied them in novel ML-algorithms, e.g. advanced Reinforcement Learning techniques. For the authors, these developments can be means to more capable engineering surrogates beyond ‘simple’ input-output-relations. Building an understanding for their fundamental behaviour in engineering tasks – as pursued in this work – certainly is a prerequisite to this. In general, DNNs consist of complex parallel and series connections of so-called „neurons“, whose individual parameters constitute the model parameters θ. Within k_trn “training episodes” θ is gradually adjusted to minimise ε_err^MSE (𝐷ⁿ,θ). See [17] for details on DNNs and their training.

Prior work focuses on emulating the scalar objective function f(φ_sim) only. However, in intricate cases, results are not as convincing [7]. Therefore, this work suggests bringing the surrogate closer to simulation results. More precisely, instead of training the surrogate to mimic the scalar objective function, i.e.

this work trains the surrogate to predict the complete strain field

Thereby, additional positional information is introduced to the surrogate: for example, the influence of each spring mainly affects its immediate vicinity on the textile. Such local influence cannot be resolved in a global scalar metric, which consequently leads to a loss of information in the database. Training the surrogate on field-data retains this information and may thus increase accuracy.

2.3 Surrogate-based Optimisation

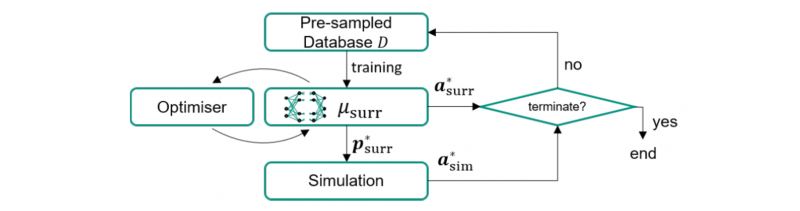
The obtained surrogate model μ_surr from Section 2.2 can be used for SBO. However, being an entirely statistical model, μ_surr inevitably introduces deviations compared to the original function φ_sim. Therefore, a single optimisation on μ_surr may not yield the true optimum of f(φ_sim(p)). SBO aims at iterative removal of these deviations by sequential updates with new observations (simulations). A common approach is to directly evaluate the found optimum p^*_surr of μ_surr, i.e. evaluating a^*_sim=φ_sim(p^*_surr).

The new observation (p^*_surr^{, a*}_sim) is then fed back into the database 𝐷ⁿ and training continues for k_trn episodes (gradient-descents). Thereby the surrogate refines in vicinity of potential optima and explores its most promising parameter regions until triggering of a termination criterion. Figure 2 illustrates the approach schematically.

Fig. 2. Scheme of surrogate-based optimisation as applied in this work.

3 Results and Discussion

3.1 Surrogate Construction

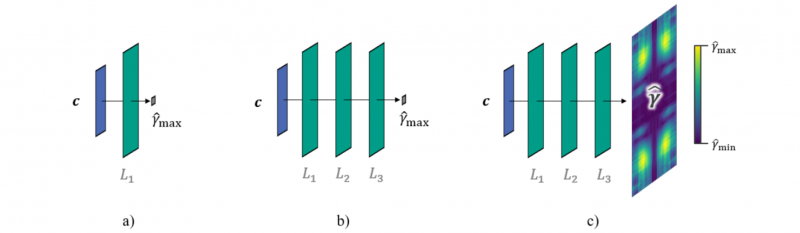
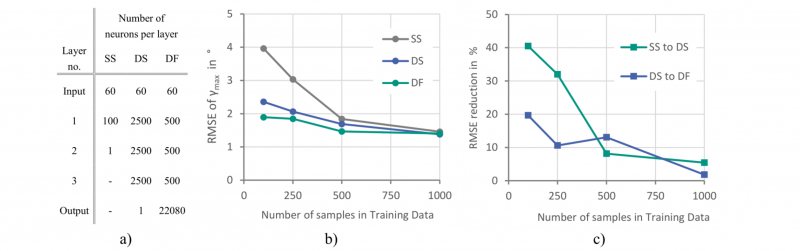
This work investigates the effect of different surrogate strategies at the example of artificial neural networks (ANNs). More specifically, two effects are studied: first, the effect of depth of ANNs (i.e. number of layers) and, second, the effect of full-field-data instead of scalar-data during model training. To this, three types of ANNs are considered as shown in Fig. 3. the SS-type (shallow network, scalar information), the DS-type (deep network, scalar information) and DF-type (deep network, field information).

Fig. 3. Visualisation of the three considered network types: a) SS-type (shallow network, scalar information), b) DS-type (deep network, scalar information) and c) DF-type (deep network, field information).

Each network is a feed-forward network whose layers are fully connected. All neurons use ReLu-activation. For each network type (SS, DS, DF) an extensive hyperparameter study was performed to determine an optimal number of neurons and layers. The studied networks range from 25 to 10 000 neurons per layer and 2 to 5 hidden layers. Since the number of parameters is much larger than the number of supplied data points, i.e. highly flexible network, measures were investigated to prevent overfitting, such as dropout, L1- and L2-regularisation, mini-batches and batch normalisation. Yet, only the mini-batches and batch normalisation proved useful. The selected network architectures are summarised in Fig. 4 a).

To evaluate each network’s data efficiency, different-sized databases n∈ {100,250,500,1000} are sampled. Performance is evaluated on an additional, separate validation set with 100 samples. For both, training and validation set, Latin Hypercube sampling is used. Figure 4 b) and c) visualise the findings.

Fig. 4. Performance comparison of three different network types with a summary of their layer-architecture a) and b) absolute and c) relative predictive error.

More specifically, Fig. 4 b) shows the evolution of prediction accuracy as measured by root mean square error (RMSE) for each ANN. For all ANNs the RMSE reduces with more available data, underpinning validity of the universal approximation theorem. However, large performance differences appear when data becomes sparse, e.g. n = 100: although trained on the same data, the SS-type cannot capture γ as accurately as the DS- and the DF-type and results in a constantly higher RMSE. Similar holds for DS- and DF-type, albeit at lesser extent. Figure 4 c) quantifies this reduction: using additional layers, i.e. changing from SS to DS, reduces the error by ≈ 40 % (100 samples). Yet, this advantage gradually becomes less significant as more data becomes available – loosely speaking, the SS-network „catches up“. Similar hold for the additional change from DS to DF since an additional ≈ 20  % (100 samples) is apparent. Therefore, it may be stated, that both measures, deepening the network and training on full-field data, significantly improves predictive accuracy, especially in sparse-data situations.

3.2 Optimisation performance

In SBO, sequential surrogate refinement with new samples is essential, for which two different paradigms prevail: samples can be placed either in parameter regions with little evidence to facilitate discovery of new, potentially better optima (“exploration”), or near already localised optima for perfection of parameter combinations (“exploitation”).

This work studies the exploration-exploitation-balance by two different hyperparameters for optimisation configuration: one hyperparameter is the initial database size n. In general, greater values of n introduce more prior information to the surrogate. Thus, it can directly exploit the most promising regions and spend less effort on additional exploration. Obviously, this comes at the cost of increased effort prior to optimisation. The second hyperparameter is the number of ANN-training episodes k_trn during SBO-loops (cf. Fig. 2). In general, the higher k_trn, the more emphasis lies on new samples during optimisation and the stronger the attraction of an optimum, i.e. stronger exploitation. Both parameters comprise two levels, n ∈ {100 ;1000} = {100;1000} and k_trn ∈ {k_min ;k_max } = {2;25}, respectively.

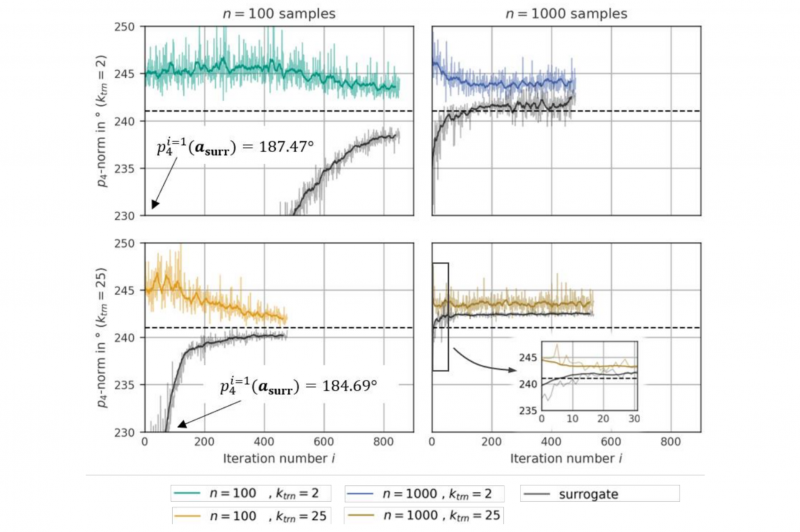
The vector-norm p_m=‖𝜸‖_m = (∑_i |𝛾_𝑖|^m)^-m constitutes the objective function. While it includes the maximum norm (m=∞) and the sum of all values (m=1) as limit cases, this work employs m=4 as a tradeoff between suppression of maximum shear and formation of shear angles in general. Fig. 5 shows the evolution of the objective function p₄(a^*_sim) and the surrogate prediction p₄(a*_surr) during optimisation. To allow investigation of long term behaviour, no automatic stopping criterion is set, but optimisations are terminated manually when both, a minimum iteration number i_min=450 and a minimum predictive error of Δp₄=|p₄(a^*_sim) - p₄(a^*_surr)| ≈ 3°, are reached.

Fig. 5. Optimisation progress for each SBO-configuration. Surrogate predictions p₄(a_surr) are given in black (moving average) and gray, while the coloured graphs represent simulation results p₄(a_sim). The initial p₄(a_surr)-values of the left column are omitted in the plot for readability. Their respective values are directly printed for reference.

Each subplot refers to a combination of hyperparameters and shows two different graphs, the surrogate prediction p₄(a^*_surr) and the actual simulation result p₄(a^*_sim). To alleviate the erratic appearance of the graphs, a moving-average over m_avg=15 iterations smoothens each curve. The dashed horizontal line denotes the best value of the objective function p^*₄(a^*_surr) ever found in this work. It is deemed the best available approximation of the true – but unknown – optimum and is thus used for reference duringsubsequent algorithm comparison.

Some volatility aside, all graphs show three common characteristics: first, the objective function p₄(a^*_sim) overall decreases which validates the general suitability of “full field”-DNNs as surrogate models. Second, the surrogate predictions approach the simulation results, corroborating the successful learning process on new samples. Third, the surrogate constantly underestimates simulation results.

The opposite holds for the right column (large database with n=1000), where both graphs show an initial descent and, from iteration 𝑖 ≈ 120 (top) or 𝑖 ≈ 10 (bottom) onwards, some wavering around a constant value. Since the surrogate is relatively accurate already at start it may directly converge to an optimum without further exploration. However, the absolute value of the objective function is higher than on the left, which implies a local rather than a global optimum.

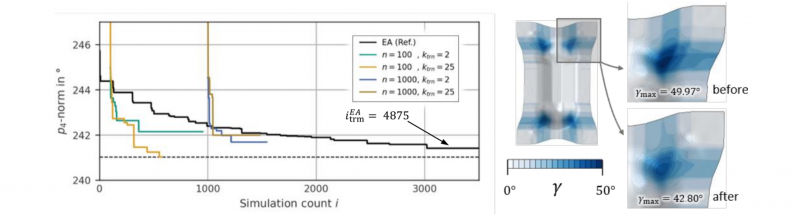
For final efficiency assessment, Fig. 6 visualises the convergence of each configuration along with a (non-surrogate) evolutionary algorithm (EA) from the DAKOTA-toolbox on default settings [18]. The graphs show the evolution of p₄(a^*_sim), i.e. the FE-simulation with the so-far-best quality metric. Formally, it is the lower envelope of the erratic graphs in Fig. 5. Note that due to initial database-sampling the graphs are offset by n=100 and n=1000 simulations, respectively.

Fig. 6. Convergence of a classical evolutionary algorithm (EA) and each SBO-configuration (left). The EA terminated in iteration 𝑖^𝐸𝐴_trm=4875 without further improvement (omitted for readability). Forming results before and after optimisation show a successful reduction of γ_max (right).

The graphs distil the essence of the previous plots: despite a faster descent of the objective function, the optimisation results with the large database 𝐷¹⁰⁰⁰ are inferior to the smaller database 𝐷¹⁰⁰. Not just in terms of quality but also efficiency: While configuration “n=100, k_trn=25” has found its final result in iteration 𝑖≈600, the “n=1000”-configurations require 𝑖≈1100 and 𝑖≈1300 iterations, respectively. Please note, that each SBO outperforms the EA in terms of efficiency and “n=100, k_trn= 25” also in terms of quality. Please also note, that “n=100, k_trn= 2” might have given a similarly good result, but was manually terminated due to excessive computation time (>10 weeks). At this time, the objective function was still descending, albeit at slow rate (cf. Fig. 5 top left). From an engineering perspective, Fig. 6 (right) shows a successful reduction of maximum shear by ≈ 7.2 ° or ≈ 14.3 %, respectively. After optimisation, the grippers restrain the material draw-in such as to avoid local shear concentration but make the deformation stretch over a wider expanse.

4 Summary and Conclusion

This work examines the use of deep neural networks as surrogate models in virtual manufacturing process optimisation at the example of gripper-assisted textile forming. Different network types are compared. Best prediction performance is achieved using a deep neural network which predicts the full strain field instead of just a single performance scalar. The network is also integrated in an SBO-framework to study suitability and convergence behaviour during optimisation. Four SBO-configurations with different exploration-vs-exploitation balances are investigated. In each case, the developed SBO-framework outperformed a current state- of-the-art evolutionary algorithm in terms of efficiency. One case gave an even better result. Results further hint that “online”- simulations during SBO-loops contribute significantly more to convergence than “offline”-simulations from prior sampling.

Further research is still envisaged. The presented results show that a smaller database – and thus a less accurate surrogate (!) – can indeed lead to better optimisation results. This observation requires a more comprehensive investigation and more ideally, a quantifiable criterion towards selecting the size of the initial database. It also implies that global accuracy metrics, e.g. MSE, might not be the best measure for surrogate quality assessment in SBO. In the long term, surrogate models may also be equipped with additional capabilities: as shown in [19], convolutional neural networks (CNN) are able to learn system dynamics from data and predict physical effects in real-world engineering problems. First results for textile draping appear promising: [20] and [21] hint that CNNs can learn to assess formability of new components from generic draping examples. [22] further shows that – in principle – CNNs can additionally be used to estimate optimal process parameters for new components. Thus, DL-techniques appear a promising and efficient tool for process design at early stages of product development.

Acknowledgment

The authors would like to thank the German State Ministry of Science, Research and the Arts of Baden-Württemberg (MWK) for funding the project “Forschungsbrücke Karlsruhe-Stuttgart”, which the presented work is carried out for. The work is also part of the Young Investigator Group (YIG) “Tailored Composite Materials for Lightweight Vehicles”, generously funded by the Vector Stiftung.