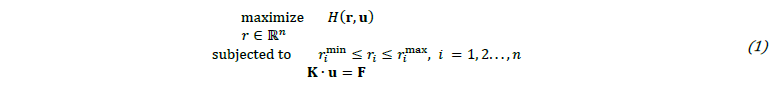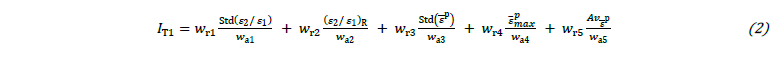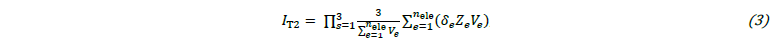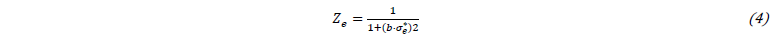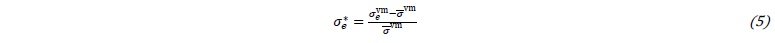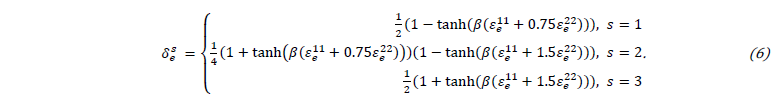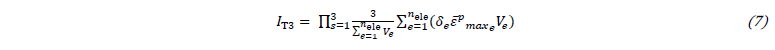1 Introduction

A competitive company needs to produce faster, with better quality and with the least waste of resources. The use of numerical simulations for the manufacturing virtualization can improve its productivity. For an accurate material behavior prediction, it is often required a complex material constitutive model and the identification of the respective material parameters. Currently, classical tests are the standard in the prediction of material macroscopic behavior. However, several of these mechanical experiments are required for the identification process, originating a very time and cost consuming process. Besides, these provide the stress and strain results for a fixed stress state, which do not resemble the complex stress and strain fields originated in many manufacturing procedures [1]. More complex mechanical tests, providing different stress and strain fields are required for a better material parameter identification and thus, a more precise material behavior prediction. Complexity can be introduced thanks to non-standard specimen geometries, complex loading conditions or a combination of both.

Many scientific advances on the specimen's geometry were based on trial and error attempts on uniaxial and biaxial loadings, generating heterogeneous strain fields. These were mainly based on uniaxial tests on perforated specimens [2], notched specimens [3], shear-like tensile zones on samples [2] and other more complicated shapes [4, 5]. Regarding the biaxial loading, it was intensively studied the cruciform shaped sample with differences on some geometrical parameters [6, 7] as well as introducing perforations[8, 9]. Concerning the optimization approaches, interesting studies have been made using shape optimization of the specimen outer boundaries in [10] and topology optimization in [11, 12].

The success of heterogeneous mechanical test for the material parameter identification was proved in [1–4, 6, 9, 10, 13–15]. It was concluded in [1, 6, 16] that parameter identification from heterogeneous specimens outperforms the one using classical homogeneous tests, such as uniaxial tensile test. Experimental procedures performed in [2, 11, 17–19] on this type of specimens also demonstrated its reliability. Furthermore, it was proved that heterogeneous mechanical tests can reduce the number of the required experimental classical tests for the material parameter identification [9].

The work developed in [10, 20–22] generated an experimentally validated butterfly-type specimen for uniaxial loading using shape optimization of the exterior contours. Nevertheless, the boundaries irregularity of the specimen generates problems related to the slipping of the grips and difficulties in the strain measurements near the edges.

The present work aims to design a uniaxial tensile load test that presents heterogeneous strain paths using shape optimization methods. The design universe is focused on the specimen's interior notch shape. The outer boundaries of the sample are rectangular, which makes the testing procedure similar to a standard tensile test, reducing the slipping of the grips. The proposed solution is expected to reduce the number of required mechanical tests and, consequently, acquire higher quality on numerical simulations of the materials due to better calibration of complex constitutive models.

2 Methodology and Implementation

2.1 General Methodology

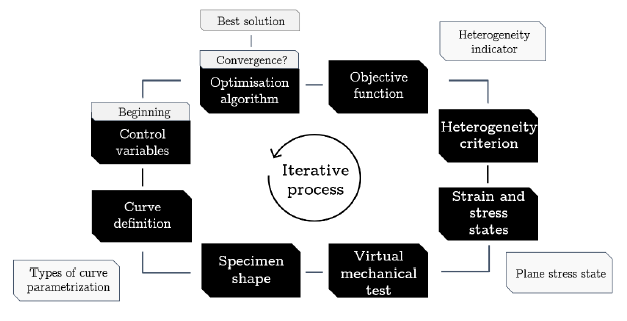
An iterative optimization process was used to design the heterogeneous specimen, as depicted in Fig. 1. The process starts by defining the design variables of the optimization procedure. For the definition of the specimen shape, different curve parameterization can be used. The specimen exterior contours are established and constant during the process. The uniaxial tensile-load test is simulated until rupture and the resulting strain and stress fields are evaluated using a heterogeneity criterion, which rates the strain field of the experiment by quantifying the mechanical information. This criterion is used as objective function of the design variables. Thus, this optimization procedure searches for a shape of the interior notched specimen that generates the largest number of heterogeneous strains and stress states during the test until rupture.

Fig. 1. Iterative process methodology for the design of the heterogeneous specimen

2.2 Problem Formulation

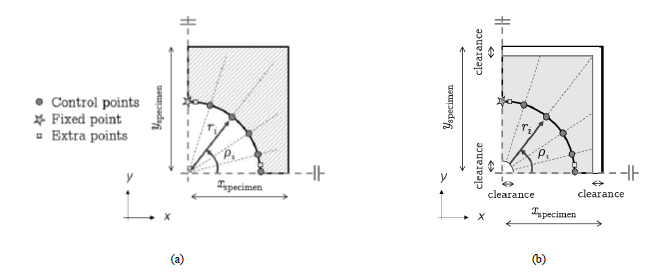
The iterative process aims to maximize the heterogeneity of the specimen, by varying the shape of the curve. The interior notched curve is defined by 𝑛 control points, as shown in Fig. 2a. Besides, one fixed point is inserted to give more flexibility to the curve, having in consideration the specimen’s weight/width ratio analysis that was performed and the assumption of the scalability of the specimen geometry. Also, two extra points are inserted to assure the C¹ spline’s continuity and the curve smoothness in the symmetries. The location of the control points are the design variables. Also, for reducing the number of the optimization variables, only the radial coordinates of the curve were considered. The angular space was equally split for the number of control and fixed points and a search space was defined, as shown in Fig. 2b.

Fig. 2. Representation of the specimen perforation and (a) its curve control points and (b) their search space

Therefore, the aim is to find the vector of optimization variables 𝐫, that maximizes the specimen's heterogeneity 𝐻, having in consideration the forces equilibrium of the test’s numerical analysis, until rupture (𝐊∙𝐮=𝐅). The problem can be formulated as:

2.3 Solution’s Evaluation

To analyze the mechanical test's richness, the strain or the stress states can be used. The strain states are defined using the minor and major strain ratio 𝜀₂/𝜀₁, whereas the stress states are calculated concerning the ratio between the minor and major stresses σ₂/σ₁. The level of strain reached during the test is also an important factor, and it is intended to go beyond the levels attained in classical tensile tests over a large area of the specimen. The equivalent plastic strain ε̅^p is a standard indicator particularly important to measure the level of plastic strain reached during the mechanical tests [23].

In this investigation, three different heterogeneity indicators where analyzed. The first is an adaptation of the heterogeneity criterion used in [10] and is given as:

It has in consideration the strain state range (ε₂/ε₁)_R, the strain state standard deviation Std(ε₂/ε₁), the equivalent plastic strain standard deviation Std(𝜀̅^p), the mean of each strain state maximum equivalent plastic strain and maximum equivalent plastic strain of the test ε̄^p_max and the average deformation Av_ε̅p. These terms have relative weights w_r1, w_r2, w_r3, w_r4, w_r5 and absolute values w_a1, w_a2, w_a3, w_a4, w_a5 for the terms adjustment of importance and normalization. The maximum possible value of the indicator is 1. For this indicator, the cost function to be minimized is CF_T1=2−𝐼_T1.

The second indicator used was an adaptation of the one proposed in [12]. The original indicator was developed and used for a topology optimization method and considered the numerical elements' density ρ_𝑒 that was here replaced by the elements' volume 𝑉_𝑒. It benefits solutions with less stress concentrations, and can be written as:

where 𝑠 denotes indexes defined in Eq. 6, corresponding to a stress state. In this case, 1, 2, and 3 indicate compression, shear, and tension stress states, respectively. The total element's number 𝑛_ele are analysed, either under plastic or elastic deformation. The term 𝑍_𝑒 penalizes solutions with stress concentrations and non-stressed material, given as:

where 𝑏 is a constant for the penalization "aggressiveness" (fixed as 3) and 𝜎_𝑒^* is calculated as:

where 𝜎_𝑒^vm is the von Mises equivalent stress of element 𝑒, and σ̅^vm is the mean von Mises equivalent stress value of all elements. The operator δ_𝑒^𝑠 filters the elements correspondent to the 𝑠 stress state [12]. δ_𝑒^𝑠 takes approximately the value of one if the element is in the 𝑠 stress state and zero otherwise. This is achieved via a 2D generalization of the smooth Heaviside function, being formulated as:

The larger is the indicator 𝐼_T2, the more heterogeneous is the solution. So, the cost function to be minimized is 𝐶𝐹_T2=−𝐼_T2.

The third indicator studied was another adaptation to the indicator proposed in [12]. Instead of evaluating the stress concentrations, it was taking into consideration the equivalent plastic strain value of each element, using:

The goal of this indicator is to benefit solutions with larger ε^̅p values and strain state diversity. The remaining equation's terms were evaluated similarly to the indicator 𝐼_T2. The cost function to be minimized is 𝐶𝐹_T3=−𝐼_T3.

3 Analysis and Results

First, it was performed a variable dependency analysis of several parameters. These were the elements’ types CPS4, CPS4R and CPS8R [24], as well as the elements’ edge dimensions of 1 mm, 0.8 mm, 0.5 mm, 0.3 mm, 0.2 mm, and 0.1 mm. These elements have 4 (CPS4 and CPS4R) and 8 nodes (CPS8R) and present complete (CPS4) and reduce integration (CPS4R and CPS8R) approaches. It was also analyzed the objective function using the three different heterogeneous indicators previously mentioned and the position of the fixed point, either in the vertical symmetry or in the horizontal one. Besides, it was tested 4, 5, 6, 8, 10, 12 and 14 curve control points, as well as the specimen’s height/width ratios of 5.30, 4.42, 4.08, 3.31, 2.65 and 2.21. Moreover, it was used a circular interior notch, an ellipse-like shape and a cross-like shaped one as the initial solution. The Nelder-Mead algorithm and a differential evolution algorithm were evaluated.

As reference solution, it was established the best solution obtained out of the optimization procedure, with an initial circular interior notch specimen shape, with a 10 mm radius. This solution had a non-parametric finite element mesh with CPS4R elements of 0.3 mm along the edges. The cost function used was 𝐼_T1 (Eq. 2). The reference solution was obtained using 5 curve control points, and a fixed point in the vertical symmetry. This specimen’s height/width ratio was 5.30, which overall refers to a specimen’s height of 265.0 mm and width of 50.0 mm. The optimization algorithm used was the Nelder-Mead, a direct search type.

Afterward, the mentioned parameters were varied independently, and the optimization process completed. The parameters that independently originated a specimen with the best cost-function value were elements of 0.3 mm edge size and CPS4R type, a 2.65 height/width ratio, an initial solution of an ellipse-like interior notch, 6 curve control points, a fixed point in the vertical symmetry and the Nelder-Mead algorithm. The solution obtained with the combined best parameters was evaluated both with 𝐼_T1 and 𝐼_T3, since they were the most interesting indicators.

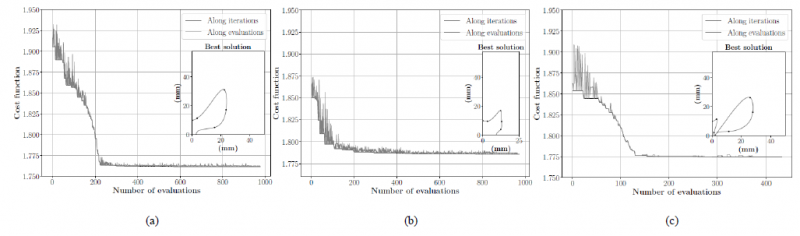
Considering the several design optimization procedures and the originated mechanical richness, the most interesting specimens obtained were highlighted. Those are originated using the parameters of the reference solution but changing only the height/width ratio to 2.65 (solution A); the second solution is obtained using the parameters of the reference solution, but the initial solution was an ellipse interior notch (solution B); and finally, the third solution is obtained with the combination of the best parameters that were analyzed independently (solution C). All these solutions were obtained using 𝐼_T1 indicator as cost function. The solutions are depicted in Fig. 3, along with its cost function value for each optimization’s process evaluation. The three optimization procedures show convergence after approximately 200 evaluations.

Fig. 3. Cost function evaluation and best obtained solutions’ geometry for solution (a) A, (b) B and (c) C

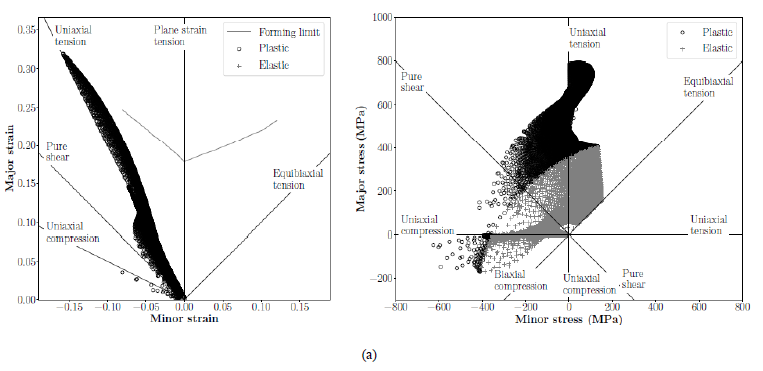
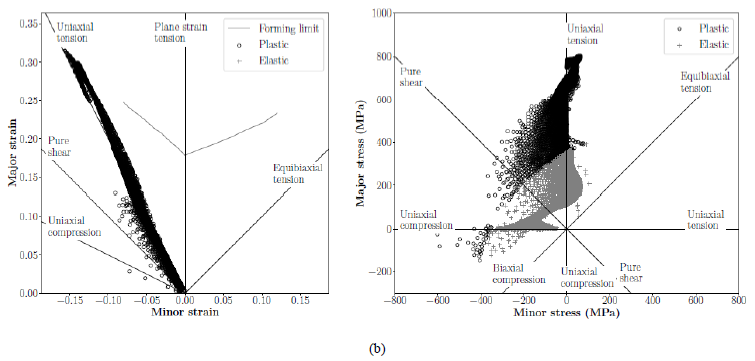
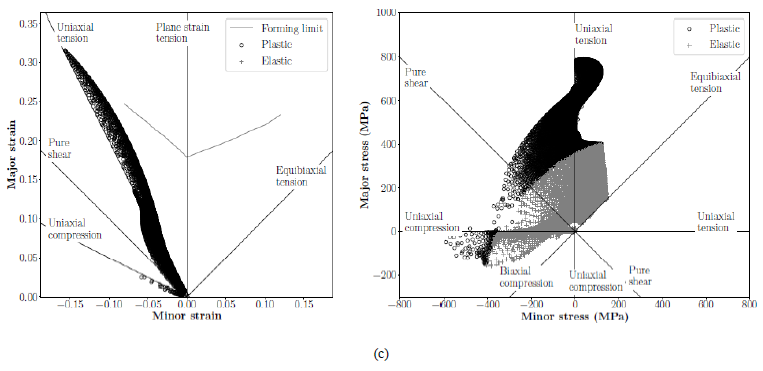
Fig. 4 shows the minor and major strain and stress diagrams of the best-obtained solutions at the moment just before rupture. Solution A and C show very similar principal strain and stress diagrams. They show stress states around the uniaxial tension, uniaxial compression, and pure shear in the plastic region. Furthermore, they also present equibiaxial tension stress state but with smaller intensities. Solution B shows poorer strain and stress states represented in the diagrams, having a predominance of the uniaxial tension state. Moreover, it has some elements exhibiting uniaxial compression and pure shear in the plastic region. It is important to note that the compressive stresses can generate local buckling, which is not intended. This possibility should be further analyzed. This issue could be minimized using a constraint during the optimization process.

Fig. 4. Minor and major strain and stress diagrams of the best obtained solutions at the moment just before rupture, for solution (a) A, (b) B and (c) C

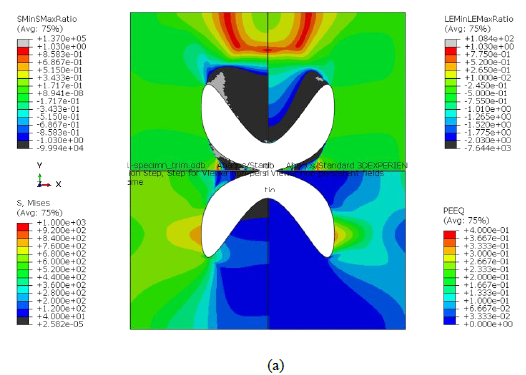
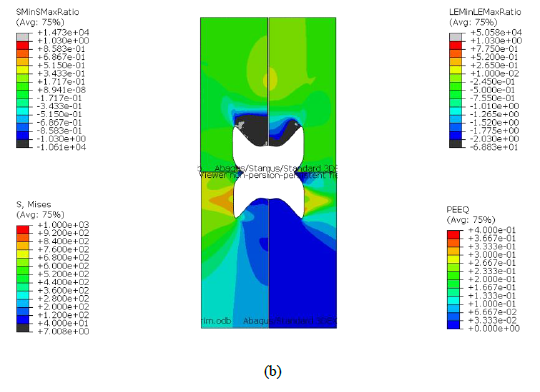
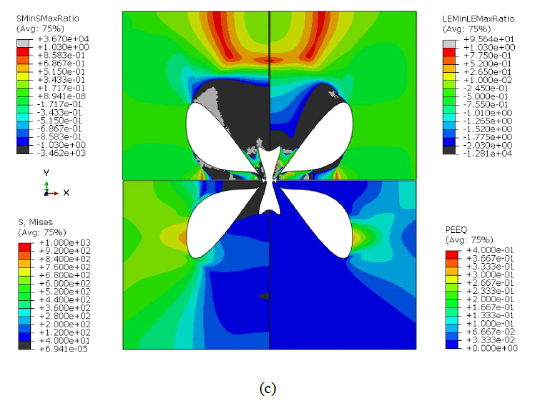
Fig. 5 presents the minor and major stress (SMinSMaxRatio) and strain ratios (LEMinLEMaxRatio), von Mises stress (S, Mises) and equivalent plastic strain (PEEQ) at the moment just before rupture of the final achieved solutions. Since there is no PEEQ in the bottom and top parts of the specimens, it is expected no interference with the grips in the experimental test, except for solution A. In terms of minor and major strain and stress ratios, it can be noticed in all solutions that the surrounding top and bottom of the interior notch show shear and compression states, whereas the majority of the specimen reveals tension state. Note that solutions A and C show different strain states in the middle area of the specimen and not just near the interior notch border. However, they exhibit some elements within the plane strain state in the specimen’s top and bottom part, which might interfere with the grips in the experimental data acquisition. The interior notch that solution C presents looks like two holes, but it is just one. This geometry might reveal some troubles concerning the manufacturing of the specimen.

Fig. 5. Best obtained solutions’ minor and major stress and strain ratios, von Mises stress and equivalent plastic strain at the moment just before rupture, for solution (a) A, (b) B and (c) C

4 Conclusions and Future Works

It was developed an approach to virtually design by optimization a heterogeneous specimen. This is a symmetric specimen for a uniaxial tensile load test. The originated specimen can be tested using a universal tensile test machine with no need for special grips. It was developed a methodology to iteratively perform the numerical test and, by the means of an optimization algorithm, obtain the richest specimen in terms of mechanical behavior. A heterogeneity indicator was used to rank the generated solutions in terms of mechanical richness. There were analyzed parameters related to the numerical analysis, to the specimen’s geometry and to the optimization procedure. All of them demonstrated to have influence in the process and are the reason for the local minimums found and strain and stress states predicted errors. The best-obtained parameters were used all together so that an even better solution would be generated.

Three geometries that present the best cost function value were analyzed. These specimens exhibiting a butterfly interior notched shape, produce uniaxial tension and pure shear states in the plastic regime, as well as uniaxial compression state mainly in elasticity. Besides, solutions A and C show equibiaxial and plane states within elastic deformations. None of the obtained geometries revealed the biaxial state.

When using the heterogeneity indicator 𝐼_T1 for comparison, it was proved that for a uniaxial tensile load test, a rectangular specimen with a non-circular interior notch in the center displays larger heterogeneity than a circular one.

The reliability of the developed tests must be verified by performing the experimental test along with the material parameter identification. Also, a more complex constitutive model could be applied to simulate more accurately the material mechanical behavior.

Acknowledgements

This project has received funding from the Research Fund for Coal and Steel under grant agreement No 888153. This work was supported by the European Research Project VForm-xSteels: “Toward virtual forming and design: Thermomechanical characterization of advanced high strength steels through full-field measurements and a single designed test”, project number 888153 [2020].

The author also gratefully acknowledge the financial support of the Portuguese Foundation for Science and Technology (FCT) under the projects PTDC/EME-APL/29713/2017 (CENTRO-01-0145-FEDER-029713), PTDC/EME-EME/31243/2017 (POCI-01-0145-FEDER-031243) and PTDC/EME-EME/30592/2017 (POCI-01-0145-FEDER-030592) by UE/FEDER through the programs CENTRO 2020 and COMPETE 2020, and UID/EMS/00481/2019-FCT - FCT - Fundação para a Ciência e a Tecnologia; and CENTRO-01-0145-FEDER-022083 - Centro Portugal Regional Operational Programme (Centro2020), under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund.