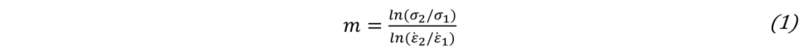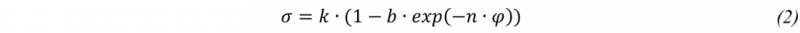1 Introduction

Ever increasing demand to reduce thickness in the packaging steel market requires a steadily development of higher strength packaging steels. Those packaging steels show just little amount of elongation in tensile test due to temper rolling to reach the required strength level. Thus, due to strong pre-hardening, geometric softening exceeds the physical hardening early on and the Considère criterion [1] is reached at only little elongation level. Low carbon contents and continuous annealing processes cause slip bands in aged conditions, relevant as most packaging steels undergo a heat treatment in the downstream lacquering process. Lüders [2] was the first to investigate the occurrence of slip bands. The yield point drop results from interstitial atoms pinning at dislocations. Within the beginning of plastic yielding in adjacent parts plastic deformation starts not until the stress in the deforming area rises above the level of the yield point. The phenomena of the yield point drop was described by Hall et al. [3] comprehensively. As well, Sylwestrowicz et al. proposed the first approach describing the velocity of the slip band front of mild steel [4]. The problems and characteristics arising in the characterization of packaging steel for finite element simulations resulting from the occurrence of slip bands in tensile tests were investigated by Knieps et al. recently [5]. Due to a strong strain localization, in some cases failure occurs already before the expansion of the slip bands over the whole specimen. At the same time, demand to simulate packaging steel forming processes increases rapidly. Basis of every simulation is always the distinctive material characterization to describe the respective elastic and plastic forming behaviour. Commonly, material is therefore tested in standardized tensile tests as the uniaxial stress state allows a simple flow curve extraction until tensile strength. As in real forming processes, e.g. the forming of aerosol tops, high deformation occurs, it is very important to receive a highest possible elongation level in tensile testing to enable a feasible extrapolation. Besides the specimen preparation method, testing speed and the specimen geometry are assumed to have a significant influence on the possible elongation level.

The general strain rate influence on the elongation prior and beyond necking mainly induced by the strain rate sensitivity of the material and thus on the total elongation is widely investigated. Ghosh [6] described the significant necking stabilization by positive strain rate sensitivity and therefore higher elongation beyond necking. The strain rate sensitivity factor m was stated as in the following eq. (1) (σ: yield stress and ε: strain rate). As well, Ghosh [6] described the necking postponement at lower strain rates for strain rate sensitive materials. This reveals the potential to receive more elongation prior to necking at lower strain rate.

Likewise, there is also strain rate dependency in the expansion of slip bands. Magd et al. [7] explored a proportional relationship between slip band velocity and strain rate since the stress reduction after reaching the upper yield point occurs not abruptly at high strai-rates, but gradually and extends over a wider range of strain. In 2003 Sun et al. [8] proposed a model, which expresses Lüders strain as a function of gauge-length strain rate. Therefore, it can be assumed that a lower strain rate leads to a lower Lüders strain for strain rate sensitive materials. Combining the two effects of a postponed onset of necking and a lower Lüders strain by a lower strain rate, a higher level of elongation is expected for packaging steel as the adjustment of an homogenous forming condition prior to necking is favored by a lower strain rate. This effect has not been investigated yet and is part of this research.

Furthermore, downscaling of specimen geometries is a feasible and common procedure to reach higher elongation in tensile testing. Merklein and Hoffmann [9] optimized the testing procedure of miniaturized tensile testing specimens. However, the testing procedure was investigated for specimen with a thickness > 1 mm. Therefore, this work aims to show the effect of miniaturized tensile test samples on packaging steel with a thickness < 0.5 mm.

2 Materials and Experimental Procedure

To investigate the influence of testing speed and specimen geometry the packaging steel TH415 with a thickness of 0.28 mm was tested. This material is characterized by a low carbon content of 0.04 wt. % and a yield strength of about 415 MPa. Due to the lacquering before forming, the material has to be tested in aged condition (20 min at 200 °C) to simulate the forming behaviour in the downstream process. However, this aging causes significant occurrence of slip bands. Together with temper rolling and thus a strong pre-hardening this results in only little elongation observed in tensile tests.

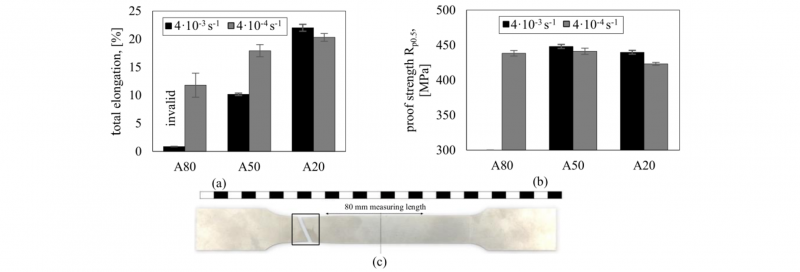
Tensile tests were carried out using Zwick Roell testing machine and two different strain rates of 4·10^-3 s^-1 and 4·10^-4 s^-1. Therefore, the testing velocity was kept constant during the elastic and plastic deformation. ISO 6892-1:2019 [10] proposes two different tensile testing geometries for sheet metal specimens in the thickness range between 0.1 mm and 3 mm. A measuring length of 80 mm and a minimum parallel length of 90 mm specifies the A80 geometry while a measuring length of 50 mm and a minimum parallel length of 57 mm characterizes the A50 geometry. To investigate the effect of a miniaturized specimen geometry the standardized A50 geometry was downscaled to a measuring length of 20 mm (in the following referred to as A20). Fig. 1 presents all investigated geometries. To ensure comparable results and to minimize the effect of edge cracking, all specimens were prepared using milling technique with equal settings. However, the preparation methods is assumed to have a huge influence on the reached elongation but this effect was not considered in the present investigation. To measure the change in length direction for the A80 and A50 specimens a strain extensometer was used. Due to the unstandardized specimen geometry, this was not possible for the A20 geometry. Thus, strain was measured using a digital image correlation system by Fa. GOM (ARAMIS 5M). For all combinations of geometry and speed three specimens were tested to ensure valid and reproducible results.

Fig. 1. Specimen geometries (a) A80 (b) A50 (c) A20.

3 Results

To assess tensile test results, technical stress over technical strain is considered. Fig. 2 compares the maximum received elongation until failure (a) and the proof strength at 0.5 % plastic strain (b). For the tensile test with a measuring length of 80 mm and a strain rate of 4·10^-3 s^-1 only very little elongation was reached (< 1 %). Looking more closely at the tested specimen it becomes obvious that failure occurs during the slip band expansion outside the measuring area and are therefore not valid. This phenomenon is underlined by Fig. 2 (c). A significant increase in elongation is observed using smaller testing geometries. Thus, using the A50 geometry already 10 % elongation could be reached while for the downscaled A20 specimen over 20 % elongation were measured using the same strain rate. Assessing the results, it is very important to consider the forming condition at the moment of failure. Therefore, Table 1 gives an overview about the forming state at failure. For the strain rate of 4·10^-3 s^-1 the significant increase in elongation by reducing the measuring length can explained by the reduced distance to overcome in the slip band expansion. For the A80 geometry, failure occurs already before the slip band expansion reaches the measuring area as already described while for the A20 geometry a homogenous forming condition and thus Lüders strain is reached. As well, the reduction in the measuring length is accompanied with a simultaneous reduction of the total number of defects and imperfections that may possibly lead to an early failure and results in an increased elongation. This reveals great potential of miniaturizing the specimen geometry for materials showing slip bands and a low elongation level. Another way to increase the elongation is the reduction of the strain rate but only for the A80 and A50 geometry as it can be observed in Fig. 2 (a). The reduced strain rate favors the adjustment of a homogenous forming condition before failure and thus a higher level of elongation in tensile tests. The early failure of the A80 and A50 samples at a strain rate of 4·10^-3 s^-1 probably results from higher strain localization and are therefore more sensitive to edge cracking. The hypothesis of a higher local deformation at higher strain rates is discussed for the A20 specimen later on. For the A20 geometry where a homogenous forming condition could already be reached with a strain rate of 4·10^-3 s^-1 , the lower strain rate leads to slightly lower total elongation. However, for standardized geometries according to ISO 6892-1:2019 reduction in strain rate is a feasible concept to reach homogenous forming condition and thus a higher level of elongation in tensile test. As well, for the lower strain rate of 4·10^-4 s^-1 the increase in elongation by reducing the specimen size is evident. Unfortunately, a lower strain rate even represents the industrial processes significantly worse as high forming velocities occur in the relevant packaging steel forming operations. Even the higher strain rate does not reflect the process velocities sufficiently and is quite too low. To exclude the additional arising difficulties at high-speeds in tensile testing and to focus on the special behaviour of packaging steel in tensile tests in aged condition, in this investigation only quasi-static tensile tests are considered. In high-speed tensile tests challenges like keeping a constant strain rate and considering inertia effects will arise additionally [11].

Fig. 2. (a) Influence of specimen geometry and testing speed on total elongation (b) Difference in proof strength with different testing speeds (c) Failure outside of measuring length for A80 geometry and 4·10^-3 s^-1 strain rate.

Varying strain rate has an influence on the strength behaviour of the material depending on the specific strain rate sensitivity. Thus, it is important to consider the strain rate induced change in strength. Fig. 2 (b) presents the influence of geometry and speed on the proof strength measured at 0.5 % plastic elongation. For the A50 geometry, the strain rate reduction leads to a softening by about 7 MPa while for the A20 geometry a softening by about 16 MPa is evident (standard deviation approx. 3 MPa). This means a low but significant strain rate sensitivity (m = 0.012 ± 0.005).

Table 1. Overview about reached forming condition and strength parameters.

To proof this observation ultimate tensile strength (UTS) is compared but only for the A20 specimen as only for these the onset of homogenous yielding was reached for both strain rates. A reduction of 14 MPa in ultimate tensile strength is obtained by reducing the strain rate from 4·10^-3 s^-1 to 4·10^-4 s^-1, underlining the results of the proof strength. For the different geometries, the A20 specimen shows slightly lower strength parameter compared to the other geometries.

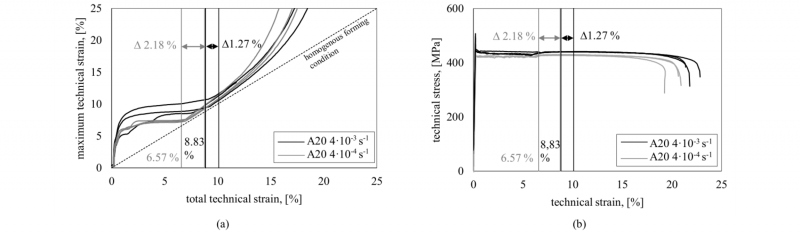
To assess the strain rate influence on the occurring Lüders strain, digital image correlation as it was used to carry out the A20 specimens is a reasonable tool. It allows detecting the local occurring deformations during the slip band expansion and can thus be used to evaluate whether a lower strain rate reduces the local arising strain for the investigated packaging steel. Fig. 3 (a) presents the maximum occurring strain in length direction over total strain in the measuring area. At the point where the maximum strain equals the total strain, homogenous yielding begins and deviates not until necking sets on. The plateau of maximum strain after the elastic area results from the expansion of local deformation bands. It is obvious that this plateau has a significant lower level for a lower strain rate as well as significant lower scattering within the three tested specimens. Quantifying the resulting Lüders strain 6.57 % for a strain rate of 4·10^-4 s^-1 and 8.83 % for the higher strain rate of 4·10^-3 s^-1 could be measured respectively averaging the three different testing specimens. This means a reduction of 2.26 percentage points by reducing the strain rate by ten times. It becomes obvious that the discussed strain rate phenomenon is also relevant for the investigated packaging steel. However, for interest of characterizing packaging steel for finite element simulation manners the area of homogenous yielding is crucial and thus the area between the described Lüders strain and uniform strain is from utmost importance. For the lower strain rate of 4·10^-4 s^-1 , uniform strain is found averaged at 8.75 % elongation while for the higher testing speed of 4·10^-3 s^-1 necking occurs at 10.10 % elongation meaning an increase by 1.35 percentage points. However, comparing the delta between uniform strain and Lüders strain the lower strain rate exhibits a wider range of homogenous yielding with 2.18 percentage points in contrast to 1.27 percentage points for the higher strain rate. This results probably from the necking postponement at lower strain rates for strain rate sensitive material as described by Ghosh. Additionally a high post uniform elongation is evident meaning 12 % elongation for both strain rates. This matches the observations by Ghosh capturing a strong necking stabilization even at a low strain rate sensitivity. For the aforementioned evaluation process to measure the Lüders strain precisely, a digital image correlation system is mandatory as it allows to capture the expansion of the slip bands. Thus, this evaluation process was only carried out for the A20 specimen as for the other specimens strain was measured using an extensometer.

Fig. 3. Relevant area of homogenous forming (a) local strain for A20 specimens obtained by optical measurement (b) stress strain data for A20 specimens.

As in real forming processes much higher deformation occurs than measured within tensile tests, a flow curve extrapolation is mandatory. Therefore, technical strain has to be converted to true plastic strain. To extrapolate the experimental data up to higher strain, the approach proposed by Voce [12] was used as stated in equation (2) (σ: yield stress, φ: true plastic strain and k, b and n: free parameters). As the experimental tensile test data can only be used in the area where a uniformity of the strain distribution is present and the assumption of a uniaxial stress state is valid, the mathematical formulation was fitted to the experimental data between Lüders strain and uniform strain. Therefore, the parameters of the Voce formulation were determined minimizing the deviation between mathematical formulation and the experimental data within the described range.

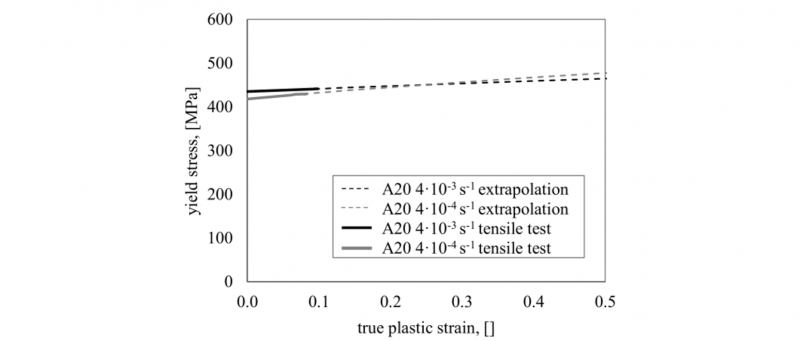
As in the area of slip band expansion due to the uniformity assumption no valid approximation is given, between the beginning of plastic deformation and Lüders strain, the flow curve is linear interpolated using the lower yield strength and the stress at the beginning of homogenous plastic deformation. Thus, in Table 2 the parameters for the flow curves are presented considering the two investigated strain rates. Fig. 4 presents the results of the estimated flow curves for the A20 specimens. Beside the Voce extrapolation for both strain rates the experimental data is illustrated. Both curves show a similar starting point resulting from only slight differences in the yield strength at different strain rates as discussed before (Table 1). There is a slight difference in the hardening prediction comparing the curve for the extrapolation of the tensile test with a strain rate of 4·10^-3 s^-1 and the tensile test conducted at a strain rate of 4·10^-4 s^-1. The higher hardening prediction at a lower strain rate is also obvious regarding the coefficients b and n of the Voce formulation in Table 2.

Table 2. Flow curve parametrization.

However, it cannot be determined finally whether the higher hardening prediction results indeed from a strain rate variation or from the extended data base at a lower strain rate. As well, the range of experimental data used for the flow curve extrapolation is even for the miniaturized testing specimens and the strain rate of 4·10^-3 s^-1 or 4·10^-4 s^-1 very small. Thus, deviations might also result from a small fitting area. The validation of the presented flow curves in customer-oriented experiments is not part of this work.

Fig. 4. Flow curve extrapolation for A20 specimens and two different strain rates using Voce’s formulation.

4 Summary and Outlook

Summarizing the results, the following conclusions can be drawn:

• Significant increase in elongation could be achieved by miniaturizing the testing specimen. At a strain rate of 4·10^-3 s^-1 the results improved from invalid fracture for the A80 specimen up to reaching 20 % elongation for the A20 specimen.

• For the standardized specimen geometries A80 and A50 the reduction of the strain rate favored the adjustment of a homogenous forming condition probably due to lower strain localization and a resulting lower edge cracking susceptibility.

• The influence of the strain rate on the Lüders strain was stated for the miniaturized specimens and a reduction in Lüders strain by about 2.26 percentage points could be observed reducing the testing speed by a factor of ten.

The highest level of elongation in the area between Lüders strain and the onset of necking (relevant for flow curve calculation) could be reached by the combination between the A20 specimen and a strain rate of 4·10^-4 s^-1. However, even for this combination only 2.18 % elongation in the area of homogenous plastic deformation can be obtained for the flow curve approximation. To enable a more precise flow curve approximation, the application of advanced methods like using bulge tests or the flow curve extraction beyond tensile strength are essential. Likewise, the influence of the preparation method was not investigated and probably shows huge influence on the reached elongation. Especially for the samples with a measuring length of 80 and 50 mm, it can be assumed that a higher level of edge quality improves the reached elongation significantly. Optimizing the milling procedure or using wire cutting to prepare tensile testing specimens possibly lead to even better results. Moreover, tensile test were only conducted at quasi-static condition. At the same time, in packaging forming processes high velocities are relevant. For a precise simulation, the plastic behaviour of packaging steel at high strain rates should be investigated.

Acknowledgements

The presented results were obtained within a cooperation between thyssenkrupp Rasselstein GmbH and the Institute of Manufacturing Technology.