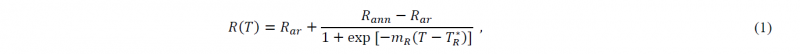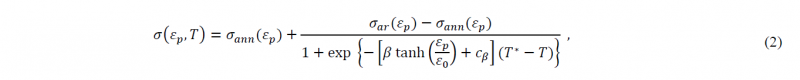1 Introduction

The environmental impact of the transportation sector, worsened by the development of the bigger urban centers, has been considered one of the main issues to be tackled over the last decade: different normative frameworks have been purposely defined in order to reduce the harmful emissions and keep the greenhouse effect under control [1,2].

Among the several solutions, the reduction of the vehicles’ masses has been indicated as the most promising one to address the mentioned problem, which can be achieved by replacing the “heavier” components (mainly manufactured using mild steel grades) with lighter structures made of Magnesium (Mg) or Aluminium (Al) alloys. It is widely known and reported that such Al alloys can ensure a sensible reduction of the masses – thanks to their competitive strength/weight ratio; on the other hand, the performance of such alloys are negatively counterbalanced by the poor formability at room temperature that limits the achievable complexity and imposes the manufacturing of sub-parts to be subsequently joined.

In the light of this scenario, the scientific research has put lots of effort to overcome such a limitation: the adoption of an increased working temperature can both improve the formability [3,4] and reduce the springback phenomena [5]; the adoption of a flexible medium for deforming the material represents another viable solution [6], which can be also efficiently combined with the warm forming approach [7]; furthermore, in the last years, a new methodology has been proposed, mainly based on splitting the process into two separate moments [8]: at first the blank initial properties are modified by short-term local heat treatment (a favorable distribution of strength-ductility can be obtained according to the component to be manufactured) so that the subsequent forming operations can be carried out at room temperature. Such an approach has been already shown its effectiveness when applied to the deep drawing (at room temperature) of 6xxx Al circular specimens (locally solutioned in the flange area) and achieving an increase in the Limit Drawing Ratio of more than 20% [9,10]. Due to the large number of process parameters involved in the mentioned innovative approach, the adoption of a numerical methodology is an unavoidable step: especially for the design of the forming operations, where an accurate material model is a key aspect to improve the quality of the numerical predictions.

Due to the heterogenous nature of heat-treated blanks, full-field measurements can offer an accurate observation of the material behaviour; an example of application can be founded in [11], where the Digital Image Correlation (DIC) technique [12] is used to investigate the hardening behaviour of LHT specimens. In particular, the local variation of material properties is expressed by employing spatial Fourier Expansions of the hardening law parameters, which are inversely calibrated with the Virtual Fields Method (VFM) [13]. As a matter of fact, coupling full-field measurements with inverse methods allows to perform the identification even on non-conventional tests. Thus, there is a wide class of identification strategies developed for the calibration of plasticity models; for instance, in [14] the Finite Element Model Updating (FEMU) technique is used to calibrate the Hill48 anisotropic plasticity model employing data from uniaxial and biaxial tests, even in the case of more complex inhomogeneous specimens, as in [15] with a double perforated specimen. Besides the FEMU approach, the VFM was employed for retrieving the constitutive parameters of isotropic hardening models [16,17], kinematic hardening models [18] and, also, anisotropic plasticity models [19,20]. Taking advantage of the larger amount of material information provided by the DIC measurement, the authors already developed an analytical-numerical characterization route geared toward the characterization the behaviour of a strain-hardenable Al alloy, previously annealed via laser treatment, with a very limited number of tests [21]. As a follow up of the proposed methodology, the attention has been focused on the anisotropy investigation, aiming at evaluating how the normal anisotropy of locally heat-treated blanks is dependent to the percentage of annealing achieved.

2 Laser heat treatment on dog-bone specimen

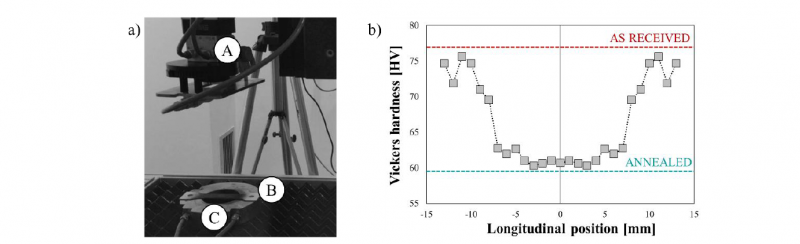
Dog-bone specimens, whose dimension were designed according to the ISO 6892 international standard, were extracted along the rolling direction from a 1.5 mm AA5754 blank, initially purchased in a pre-strained condition (H32). The specimens were then heat treated in the central region via a 2.5 kW CO2 laser unit and thus locally brought in the annealed condition: the treatment head (A in Fig. 1a) is equipped with a Diffractive Optical Element (DOE) to obtain a top-hat energy distribution over a 10 mm square spot. Before carrying out the local heating, the specimen was previously sprayed with a blank paint (B in Fig. 1a) to increase the quantity of absorbed energy and positioned on a hollow cylindrical cooler (C in Fig. 1a) to prevent an excessive heat conduction toward the ends.

Fig. 1. Laser heat treatment on dog-bone specimen: a) the adopted experimental setup; b) the resulting distribution of hardness

The specimen was heated setting the laser power at 750 W for a duration equal to 4 seconds (the values of the process parameters were defined via numerical simulation as detailed in [18]). Once cooled down to room temperature, the distribution of properties was assessed via Vickers microhardness measurements (Qness Q10+ hardness tester; load: 0.2 kg; dwell time: 5 s) along the longitudinal symmetry path: the hardness profile shown in Fig. 1b (the 0 position refers to the geometrical center of the specimen) suggests the effectiveness of the heat treatment in locally annealing the material.

3 Tensile test on LHTed specimens

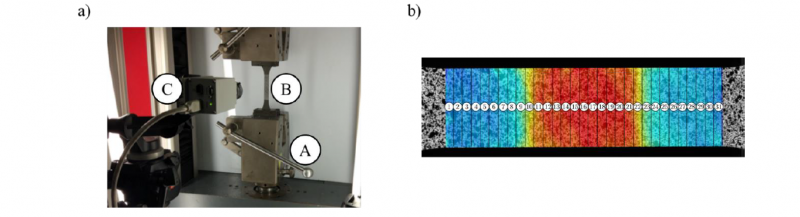
Tensile tests on the laser-heated specimens were carried out on a 50 kN Zwick-Roell electro-mechanical testing machine (A in Fig. 2a) under quasi-static conditions, thus applying a strain rate around 1E-4 s^-1. Tensile tests were assisted by the 2D-DIC system (C in Fig. 2a) pointing at the specimen’s surface (B in Fig. 2a) irradiated by the laser beam: as it can be seen from Fig. 2b, a stochastic distribution of black dots on a white matte background was created and recorded by the DIC camera (Pixelink® BU371F with an image resolution of 1280 × 1024 pixels) as a virtual grid for the full-field measurements. The deformation history was retrieved by correlating the test images via the commercial software MatchID®, employing a subset of 21×21 pixel² and a stepsize of 5 pixels.

Fig. 2. Tensile tests on laser-heat treated specimens: a) experimental setup; b) detail of the DIC measurement with an example of ROIs subdivision. The colormap depicts the uniaxial logarithmic strain distribution typically obtained on the specimen surface.

4 Investigation of the normal anisotropy

Following the approach presented by the authors in [11,22], the spatial distribution of the normal anisotropy was evaluated by subdividing the 72×20 mm² DIC gauge area into smaller regions of interest (ROIs), as illustrated in Fig. 2b. Thereby, the displacement fields belonging to each ROI was derived in order to obtain the corresponding logarithmic strain fields, according to the Hencky strain definition. Then, for each frame, the so-computed strain components were averaged through all the values included in each investigated region.

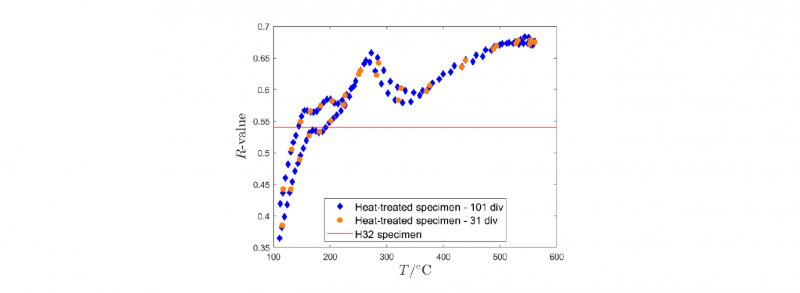
Fig. 3. Distribution of normal anisotropy according to the maximum heat-treatment temperature using two ROI’s size.

The normal anisotropy was expressed by means of the width-to-thickness plastic strain ratio, also known as Lankford coefficient and commonly indicated as R-value. Since the employed 2D-DIC technique provides only the in-plane strain components, the through-thickness plastic strain 𝜀_𝑧𝑧^𝑝 was computed by involving the volume conservation law during the plastic deformation, i.e. 𝜀_𝑧𝑧^𝑝=−(𝜀_𝑥𝑥^𝑝+𝜀_𝑦𝑦^𝑝), where 𝜀_𝑥𝑥^𝑝 and 𝜀_𝑦𝑦^𝑝 indicate the longitudinal and transversal plastic strains respectively.

Under the assumption that the treatment’s temperature is almost constant within each ROI, the normal anisotropy distribution can be correlated with the peak temperature, according to the hybrid numerical-experimental approach detailed in [22]. As already mentioned in Section 2, the laser treatment on the specimen was designed through a thermal finite element model, aimed to study the temperature profile and the treatment duration producing a predefined annealing distribution along the specimen surface. Therefore, the maximum heating temperature T from the numerical analysis was matched with the corresponding ROI from the full-field measurement, allowing to visualize the dependency of normal anisotropy with respect to different levels of annealing.

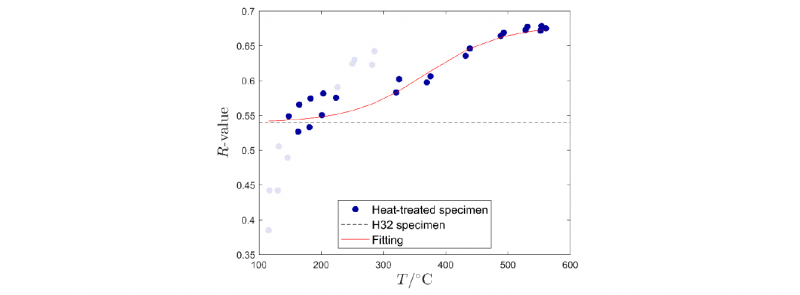
In Fig. 3, the R-value distribution vs. the maximum treatment temperature is reported for two ROIs partitions, namely 101 and 31 divisions, whose characteristic lengths correspond to 0.7121 mm and 2.32 mm respectively. Both datasets show that the R-value increases from 0.38 (measured in proximity of the peripheral areas of the specimen) to 0.675 in correspondence of the LHT zone where the material is in fully annealed conditions. It is worth noting that material points which experienced lower treatment temperatures – i.e. a minor level of annealing – are characterized by R-values below 0.54, which corresponds to the width-to-thickness ratio measured on a fully H32 specimen machined at the same material orientation; such important difference, however, can be related to the low plastic strain (<0.05) achieved in these ROIs during the test, which does not provide enough data points for a realistic reconstruction of the R-value behaviour.

The normal anisotropy trend also exhibits a steep peak at T ~280°C, which can be associated to a local alteration of stress triaxiality, driven by the rapid modification of material properties in the transition zone between the H32 and H111 regions. In fact, neighboring ROIs characterized by a different level of annealing, under the same tensile load, respond with a different deformation and strain behaviour. However, since material points at their interface must respect the displacement continuity, an additional stress component along the thickness direction appears; such stress component cannot be measured with the used DIC facilities and, in turn, not included in the R-value computation.

Despite that, the normal anisotropy alteration due to the annealing conditions can be approximated by employing a sigmoidal function, creating, also, a link with the constitutive model introduced in [22] for describing the hardening behaviour of the same heat-treated blanks; therefore, an analytic expression of the R-value can be defined as function of the maximum heating temperature with the following equation:

where 𝑅_𝑎𝑟 and 𝑅_𝑎𝑛𝑛 indicate the normal anisotropy of the as-received material and fully annealed material respectively, while 𝑚_𝑅 and 𝑇_𝑅^∗ are parameters regulating the shape of the sigmoidal function. The coefficients of the material model were inversely calibrated through the minimization of the error between the experimental and predicted R-values. In particular, the optimization problem was solved by using the SQP algorithm (Matlab® fmincon function) and the resulting values are listed in Tab. 2.

Fig. 4. Comparison between experimental R-value trend and predictions with fitted sigmoidal modelling.

Fig. 4 depicts the outcomes of the inverse calibration procedure, showing a good matching between the experimentally measured behaviour of the normal anisotropy with the predicted one. Note that R-value data corresponding to the lowest amounts of heat treatment temperature and the curve peak were not included in the identification process.

Tab. 1. Identified coefficients for the R-value sigmoidal model.

5 Numerical validation

The developed model for the description of the R-value dependency from the annealing grade was validated by means of a numerical model of the tensile test on the AA5754 heat-treated dog-bone specimen. Therefore, the anisotropic behaviour was modelled by means of a modified version of the Hill48 plasticity model, where the R₀ is expressed through the sigmoidal relationship in Eq. 1. The material modelling approach based on logistic functions was also employed for the hardening behaviour, here included following the so-called HT-hardening model:

where 𝜎_𝑎𝑟(𝜀_𝑝) and 𝜎_𝑎𝑛𝑛(𝜀_𝑝) are the flow stress curves of the as-received and annealed material respectively, 𝜀_𝑝 is the plastic strain. The hardening model coefficients were taken according to the results in [18], viz. 𝛽=0.01095, 𝑐_𝛽=0.014323, 𝑇^∗=301.85 and 𝜀₀=0.005. All the constitutive modelling framework was introduced in the Finite Element analysis via UMAT subroutine in Abaqus/Standard®.

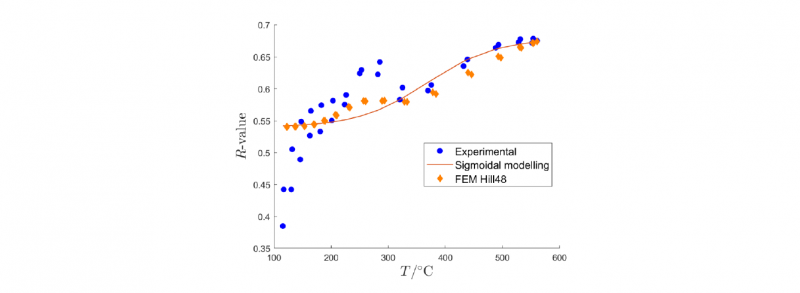
Since both hardening and R-value material models require the annealing information, the numerical simulation is based on a two-step analysis. First, the local laser heat treatment is simulated employing a transient thermal analysis in order to obtain the temperature distribution on the specimen; so, the maximum temperature of the treatment T is extrapolated for each node and employed the forthcoming 2D quasi-static structural analysis. Thus, the numerical strain fields were used to compute the associated R-value using the same procedure adopted for processing experimental data.

Fig. 5. Comparison between the experimentally measured R-value and the FEM prediction, with the proposed sigmoidal modelling.

All the results are reported in Fig. 5, where the normal anisotropy retrieved from the FE model is compared with the experimentally measured R-values and the reference sigmoidal modelling. Although there is no information about the width-to-thickness ratio in other material orientations (namely 45° and 90° with respect to the RD), the numerical analysis is capable of reproducing the normal anisotropy trend of the material at different annealing temperatures, showing a reasonable agreement with the experimental data. It is worth observing that even the numerical predictions present a marked peak at T~270°C, indicating a modification of the stress triaxiality in the zones characterized by a rapid alteration of material properties due to the localized treatment. This is an important feature to consider in sheet metal forming applications, since the stress triaxiality plays a fundamental role in ductile damage criteria which can be efficiently used in stamping simulations [23].

6 Conclusions

In the present paper, the methodology proposed by the authors in a previous research has been adopted for the characterization of the anisotropic behaviour of a strain-hardenable Al alloys in wrought conditions (AA5754-H32) locally annealed via laser heating. Tensile test on locally treated dog-bone specimens (extracted along the rolling direction) showed that the resulting gradient of properties reflected in a variation of the Lankford parameter ranging from 0.5 where the material kept its initial state up to around 0.65 in the fully annealed region; moreover, a steep peak was recorded at T ~280°C, as a consequence of the local alteration of stress triaxiality risen in the transition zone.

The experimental values of the normal anisotropy coefficient were fitted by a sigmoidal function and implemented in a modified Hill48 plasticity model: the tensile test was simulated (implementing the HT hardening model in a UMAT subroutine) and numerical results were in good agreement with the experimental measurements, even though there were no information regarding the normal anisotropy from other material orientations.

Future developments will be aimed at completing the investigation of the anisotropic behavior considering the other material orientations so that more sophisticated plasticity models can be precisely calibrated, thus improving the accurateness of the FE models for the simulation of sheet metal forming processes.

Acknowledgements

The present paper received funding from the Italian Ministry of Economic Development, MISE (Project "FORTRAIN").