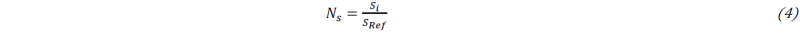1 Introduction

In recent decades, an economical goal of shortening the design-to-manufacturing period is seriously considered. The additive manufacturing (AM) technology is superior to meet the high demands related to quick alloy manufacturing [1]. Unlike any traditional manufacturing methods, AM is a layer-by-layer build with a computer-aided technique that can produce a threedimensional component directly. It offers novel design freedom and the possibility of property customization of devices, like heat exchangers, pressure valves, gas turbines, and so on [2]. In addition, more applications that require load-bearing capability are also adopting the AM technology and AM materials. Although further material forming is not needed in these structures, accurate description of the deformation and failure behavior of AM materials and correlating it with microstructure and process are crucial for the design of the AM process and structures.

Austenitic stainless steel 316L is widely studied due to its high corrosion resistance and high strength [3], and the major production methods are forging or casting [4]. AM technique provides an alternative to producing components made by 316L easily and quickly [5]. However, AM fabricated 316L specimen (AM 316L) has different microstructural features when comparing to conventional 316L. Firstly, different laser scanning strategies of the AM process would lead to various textures in matrix material during the directional solidification in a melt pool due to the unique heat transfer procedure [6,7]. Secondly, different AM process parameters can produce various laser energy densities in a melt pool, which would induce the appearance of pores within the material [8]. If the energy density is deficient, pores would lie between melt pools, which are in a state of lacking metallurgical binding [9], while if the energy density is surplus, the vapor cavities will take place and introduce pores within the local molten pools [10]. To some extent, pores cannot be entirely avoided through optimizing the AM process parameters because the powder bed is not in the perfect uniform state for a real fabricating process. Therefore, it is significant to study the influence of pores and their various characteristics on the properties of AM metals. Prasad et al. [11] investigated the influence of pore characteristics on the anisotropic mechanical behavior of laser powder bed fusion (LPBF) manufactured 316L by using a micromechanical modeling approach. It is concluded that the porosity and pore shape would influence the strength anisotropy and damage behavior significantly when the material is loaded in different directions.

In addition to the porosity, the microstructural features, in particular texture, of the metal matrix play a significant role in the final mechanical properties of the AM metals, especially for the LPBF fabricated 316L [12-15]. According to the research by Sun et al. [12] on selective laser melting (SLM) 316L steel, it has a common strong <100> texture fiber parallel to the building direction (BD), i.e. <100>//BD fiber, in an as-built sample. The same texture is also found by other researchers [13-15]. Besides, the designed novel process can also achieve <110>//BD texture of as-built 316L to enhance its tensile strength by 16% and ductility by 40% [12]. Due to textures existing in AM 316L, mechanical anisotropy of AM metals has been correspondingly influenced [16-18]. Hitzler et al. [16] experimentally studied the anisotropic tensile properties of SLM 316L, and found that Young’s modulus, ultimate tensile strength as well as fracture elongations vary from fabrication settings. The maximal strength is found by 45° layer versus loading offset. Yang et al. [17] experimentally studied the wear anisotropy of SLM 316L by applying six different sliding directions. A significant difference in scratch depths was found when the wear loading was 1 N, while it increased to 5 N, the wear behavior became similar for all directions. Charmi et al. [18] implemented a crystal plasticity (CP) model to numerically study the anisotropy of 316L built by different inclination angles relative to building direction. They concluded that mechanical anisotropy is strongly affected by matrix texture, and the following experimental results prove the numerical predictions.

In view of the current literature on the SLM 316L, it is clear to state that two scientific gaps are still wide open: i) both the porosity and texture of the matrix will influence the plastic anisotropy behavior, and studies on individual topics are evident, but the combination of them to reveal the interaction pattern has not been systematically performed; and ii) the focus of the plastic anisotropy in the AM community has been mainly on the strength, while another important and sensitive merit to describe the plastic deformation anisotropy has been seldomly investigated, which is the Lankford coefficient, i.e. the r-value.

Therefore, the current study aims to perform a systematic numerical study to reveal the influence pattern of the porosity coupled with various textures of the steel matrix on the plastic anisotropy behavior of AM steels. Besides strength and strength anisotropy, we particularly focus on the plastic deformation anisotropy characterized by the r-value.

In the study, the representative volume element (RVE) coupling CP method is applied to reconstruct the microstructural features of AM 316L, which includes different process designed crystallographic textures and various porosities (pore volume fractions). Herein, three types of matrix grain orientations (random orientation, <100>//BD fiber, and <111>//BD fiber) and three porosity (0%, 1%, and 5%) are focused to simulate. Then, mechanical anisotropy of AM 316L with specific microstructure features is numerically studied under three different loading conditions. The virtual tensile tests are carried out along building direction, recoater direction (RD), and transversal direction (TD) in respective. Herein, BD is perpendicular to the build platform, RD and TD are parallel and perpendicular to laser scanning direction on the powder bed. To characterize the machinal properties, the flow curve and r-value evolution are supposed to compare and discuss. In section 2, the RVE constructions of microstructural features containing pore characteristics and texture information are established. In section 3, the virtual tensile testing method and crystal plasticity theory are introduced. In Section 4, the results of the preliminary micromechanical modeling are mainly discussed.

2 RVE generation

2.1 RVE construction with different porosities

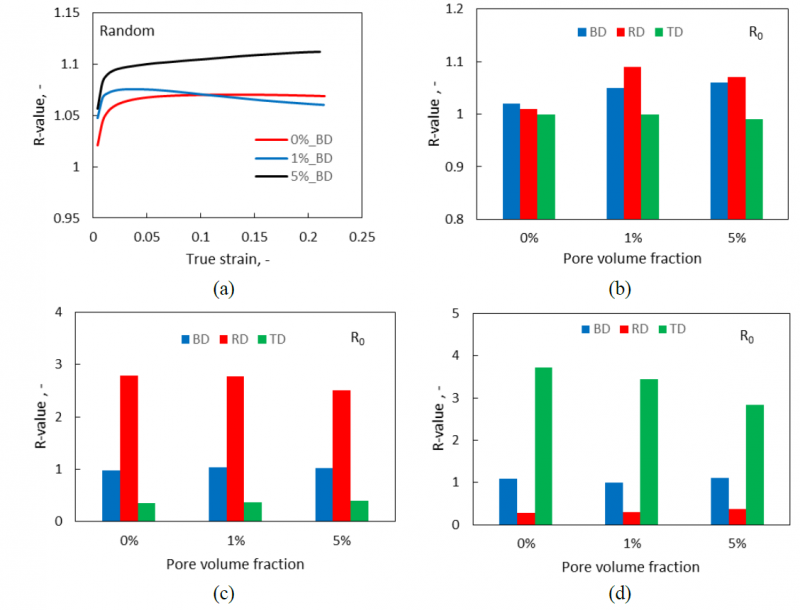
The RVE construction is aiming to represent the global microstructure of AM 316L material, including matrix grains as well as the process-induced pores. According to many experimental investigations [5,19,20], the porosities of as-built AM 316L samples vary from around 0.1% to 16% based on various process parameters, and the average grain sizes are from 9 µm to 17 µm. The pore size varies from around 5 µm to 45 µm, but 60% of the pores have a size less than 5 µm and only 3% are larger than 30 µm. In this preliminary study, the main focused features are porosity and grain orientation; therefore, the size and shape distribution of both matrix grains and voids were not explicitly considered. As a result, the average sizes of equiaxed grains and pores were chosen as 16 µm and 6 µm, respectively. The investigated porosity was defined as the pore volume fractions, i.e. 0%, 1%, and 5%. Considering the computation efficiency and calculation resolution, the mesh size and element number of a proper RVE model are set as 3 µm×3 µm×3 µm and 40×40×40 (64000 elements in total), which results in the global RVE size of 12×12×12 µm³ with total grain number around 750, as shown in Table 1. A concept of dual-phases (DP) methodology [21,22] was implemented to reconstruct the corresponding RVEs. Herein, the grain is simulated as the primary phase with a face-centered cubic structure (fcc) while the pore is considered as a secondary isotropic phase. The generated RVEs with three kinds of porosities are demonstrated in Fig. 1.

Table 1. Numerical setting and microstructural features of the investigated RVEs.

Fig. 1. Phase maps of RVEs with different pore volume fractions. (The red color represents the pores.) (a) 0%, (b) 1%, (c) 5%.

2.2 Matrix grain orientation distribution

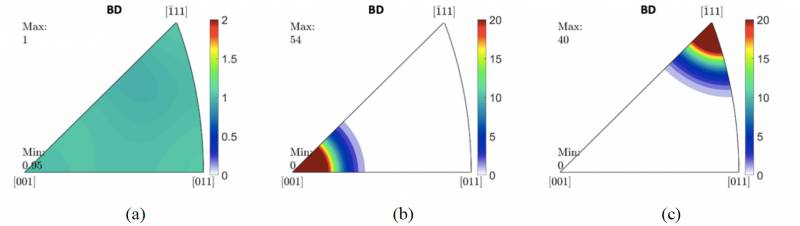
To investigate the texture effect on mechanical anisotropy of the reference material, three types of grain orientation distribution were designed, i.e. random, <100>//BD fiber, and <111>//BD fiber. The inverse pole figures of these three types are demonstrated in Fig. 2. For texture fibers, the misorientation angular tolerance was within 15° (referring to the high angle grain boundaries) from the fiber center and assigned to the matrix grains for simulation.

Fig. 2. Grain orientation distributions with BD inverse pole figures of the investigated RVEs. (a) Random orientations, (b) <100>//BD, and (c) <111>//BD.

3 Crystal plasticity modeling

The crystal plasticity model provided by the DAMASK (Düsseldorf Advanced Materials Simulation Kit) platform [23] was used to carry out the virtual tensile testing in this study. The key constitutive equations are briefly introduced in the following.

The shear rate 𝛾̇^α is determined by the resolved shear stress 𝜏^α and the critical resolved shear stress 𝜏_c^α . The kinetic law on the slip system 𝛼 is given as (1).

where 𝛾̇₀ and 𝑚 are the reference shear rate and rate sensitivity of slip system 𝛼, respectively. The micromechanical interaction between different slip systems shall also be taken into consideration by (2).

where h_αβ is the hardening matrix and given as (3).

where ℎ₀, 𝑎, and 𝜏_c^s are slip hardening parameters. The value 𝑞_αβ incorporates the effect of self-hardening (𝛼 = 𝛽) and latent hardening (𝛼 ≠ 𝛽) and is assigned as 1.0 for coplanar slip and 1.4 otherwise. The detailed explanations of the scheme and implementation with CP models have been given in many studies [24,25]. The fast Fourier transformation (FFT) approach was employed to solve the boundary conditions. The matrix grains feature the anisotropic elastoplastic deformation with crystal plasticity modeling, while the second phase follows the isotropic elastic deformation with a very small number to mimic the behavior of voids. The crystal plasticity parameters of AM 316L grains were referred to [11]. The elastic parameter (isothermal bulk modulus) of air gas [26] was employed for voids. With this method, the anisotropic mechanical responses of the whole material along different loading directions (i.e. BD, RD, and TD) could be predicted, including both the flow curves and r-value evolution curves to evaluate mechanical responses of the AM steel. The specific material parameters of the two phases are given in Table 2.

Table 2. Material parameters of the investigated AM 316L [11,26].

4 Results and discussion

4.1 Strength

Fig. 3 shows the predicted true stress of AM 316L with different porosities and matrix textures. Fig. 3 (a) demonstrates flow curves along BD loading as an example, it is obvious that the strength reduces with the increase of porosity. Pores would not affect the plastic deformation of the matrix in grain-level interactions, so its influence on strain evolution could be ignored. When investigating the pore’s influence on anisotropy, true stresses at 0.05 true plastic strain of RVEs with different grain orientations along three loading directions are chosen to discuss. A normalized parameter 𝑁_s is introduced by (4) for comparison.

where 𝑆 is the target mechanical property and 𝑖 represents the studied microstructure. The reference point 𝑆_ref is 𝜎_0.05 of microstructure with random grain orientations and 0% porosity along BD loading. As shown in Fig. 3 (b)-(d), it is clear that 𝜎_0.05 decreases with the increase of porosity. Nevertheless, the <111>//BD fiber always shows the highest stress level while <100>//BD fiber shows the smallest one. In terms of porosity, they are insignificant to grains with random orientations and <100>//BD fiber but distinctly reduce the anisotropy of <111>//BD fiber. Therefore, the influence of pores on stress anisotropy depends on the matrix orientations to some extent. Conclusively, in terms of strength, grains with <111>//BD fiber shall be preferred for the material design of AM 316L, while concerning the stress anisotropy, random grain orientations shall be naturally favorable.

Fig. 3. The predicted true stress of RVEs with different porosities and grain orientations along BD, RD, TD loading.

(a) Flow curves along BD loading of RVEs with random orientations. (b), (c), and (d) Normalized parameters of true stress at the true plastic strain of 0.05 along BD, RD, TD loading of RVEs with random orientations, <100>//BD fiber, and <111>//BD fiber, respectively.

4.2 R-value

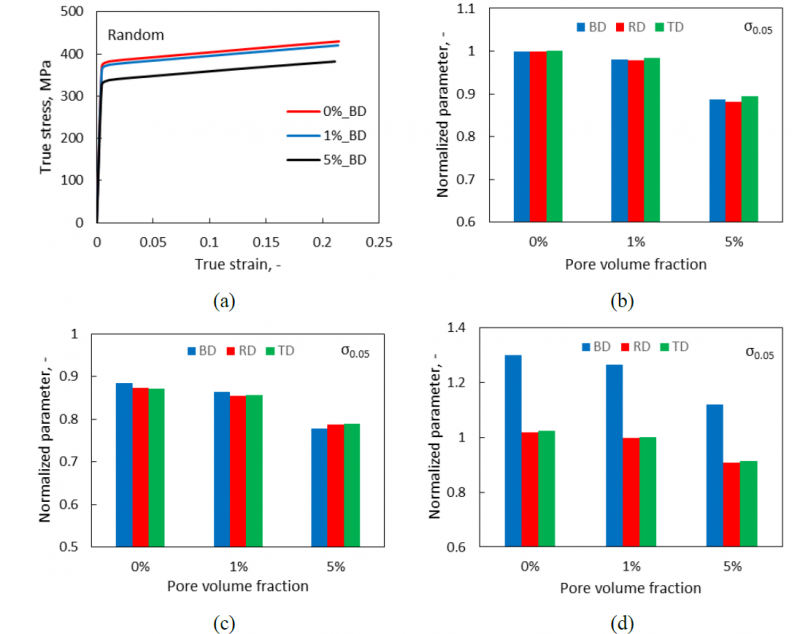
The predicted r-values of investigated RVEs are compared in Fig. 4. Herein, r-value evolution curves of RVEs with random orientations along BD are shown as an example in Fig. 4 (a). Pores enhance the r-values to some extent, especially at the early stage of deformation. In this study, the initial r-value, R_0, is chosen as the characteristic for discussion.

As shown in Fig. 4 (b), for RVEs with random orientations, all r-values are close to one (vary from 1 to 1.1), which indicates the deformation is relatively uniform regardless of porosities. However, it is noted that R₀ changes slightly from one along various loading directions. This also indicates that the random texture is not completely random, although a quite isotropic strength level is reached. It could be improved in the future with more grains consider in the calculation. Along TD loading, R₀ is seldom affected by pores, but the r-values increase distinctly along BD and RD. Furthermore, the enhancement of anisotropy is consistent with porosity along BD, however, it decreases along TD when porosity increasing from 1% to 5%.

As shown in Fig. 4 (c), for grains with <100>//BD fiber, all R₀ values along BD hold a similar value of 1. The largest scale of R₀ is found along RD, and they decrease from 2.8 to 2.5 with the increase of porosity. The smallest R₀ is observed along TD, and they increase from 0.35 to 0.4 with increasing porosity. As a result, the corresponding r-values along RD and TD are both decreasing with increasing porosity.

As shown in Fig. 4 (d), for grains with <111>//BD fiber, R₀ along BD changes slightly around 1.1, so the deformation is relatively uniform. Unlike <100>//BD fiber, the largest R₀ (from 2.83 to 3.72) is found along TD, while the smallest scale (from 0.28 to 0.36) is observed along RD. Besides, with increasing porosity, R₀ increases for RD loading while decreases for TD. The same as <100>//BD fiber, pore reduces the deformation anisotropy for RD and TD loading.

Fig. 4 The predicted R-values of RVEs with different porosities and grain orientations along BD, RD, TD loading.

(a) R-value evolution along BD loading of RVEs with random orientations. (b), (c), and (d) Initial r-values along BD, RD, TD loading of RVEs with random orientations, <100>//BD fiber, and <111>//BD fiber, respectively.

Normally, compared to strength, the r-value is strongly affected by the crystal orientation and more sensitive to the interaction between grains. For RVEs with random orientations, the anisotropy is enhanced after introducing pores. As aforementioned, the pores are set as an isotropic phase with very small elastic parameters; therefore, matrix grains are responsible for most of the strains in deformation. It indicates that the anisotropy relies more on matrix characteristics. In this study, as the limited grain number in the generated RVE, i.e., less than 800 grains, a perfect status of random orientations is not yet achieved. Thus, a slight anisotropic behavior exists in RVEs with random orientations, which is suggested by the variation of r-values along three loading directions with 0% porosity. To solve this problem, the matrix grain numbers for simulation should further increase to minimize the anisotropy. In addition, it is evident that the pores are interacting with the texture of the matrix and the resulting pattern on the anisotropic rvalues are sensitive and texture dependent. This sets a specific focus on the AM material design in the future with respect to the anisotropic deformation behavior. For a more detailed conclusion, misorientation distribution should also be considered to study the matrix grain interaction and the matrix-void interaction in the future.

5 Conclusions

A virtual laboratory coupling the representative volume element method and the crystal plasticity model is employed in this study to investigate the effects of process-induced pores on the anisotropy of AM 316L material. Herein, three types of matrix grain orientations are introduced in terms of potential scanning strategies that could be customized by the AM process. The influence of porosities on matrix with different textures are mainly discussed. The evaluated mechanical properties including strength and rvalue, the results can be used to guide the process design of AM steel. The main conclusions are drawn as follows:

• The higher porosity (pore volume fraction) is, the lower strength of the AM steel sheet is, regardless of matrix orientations or tensile loading conditions.

• Comparing two fibers in the AM 316L steel, the higher strength level is observed by grains with <111>//BD fiber, while the <100>//BD fiber shows a lower strength level, regardless of porosities or tensile loading conditions.

• With respect to strength anisotropy, RVEs with <111>//BD fiber have the highest variation regardless of porosities, but it is reduced with increasing porosity. RVEs with random orientations and surprisingly <100>//BD fiber both show very minor strength anisotropy, and the influence of porosities on the strength anisotropy is also negligible.

• The r-value is close to one along BD loading regardless of grain orientations. However, for RD and TD, RVEs with random orientations display a small variation of r-values and they are both close to one. For RVEs with <100>//BD and <111>//BD fibers, they both show large variations of r-values but an inverse tendency. The pore can reduce the anisotropy of RVEs with textures, while it does not affect the r-value anisotropy of RVEs with random orientations significantly.

• For material applications, grains with <111>//BD fiber of AM steel is preferable for application in high strength requirement. The random orientations are favorable for homogeneous deformation and medium strength level in general applications.

• In the future study, better control of pore size, shape factor, and morphology shall be developed in micromechanics modeling. Besides, the grain number and grain boundary effect would also be considered to minimize the difference among different RVE sets.

Acknowledgements

The authors wish to acknowledge the CSC – IT Center for Science, Finland, for computational resources under project 2001353.