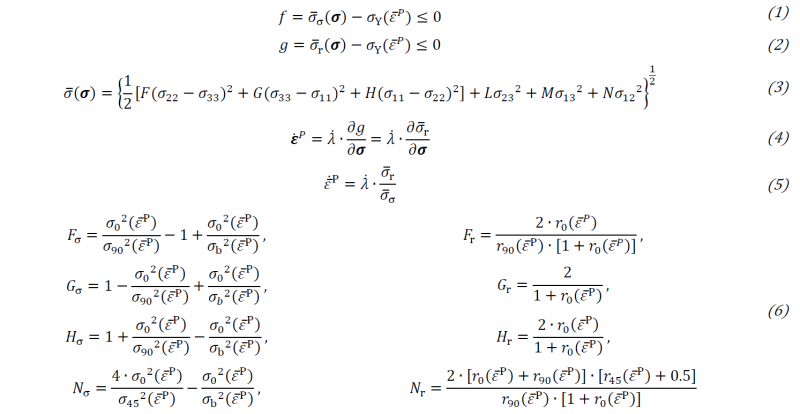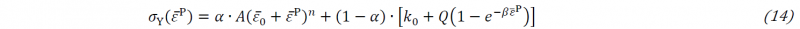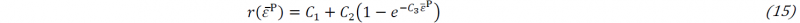1 Introduction

Dual-phase (DP) steels are usually low-carbon low-alloy materials, which have dispersed martensitic islands embedded in the ductile ferrite matrix as the microstructure [1]. Accompanying the development of advanced high strength steels (AHSS), DP steels are widely adopted in the automotive industries, due to their attractive combination of high strength with balanced ductility and good formability at low production costs [2]. However, the complexity of the damage and fracture behavior of these materials increases consequently. In order to understand and predict the failure of the material, damage mechanics model development becomes a common interest among researchers. Ductile materials tend to have strain hardening and considerably large plastic deformation as fracture response. Therefore, the ductile crack initiation and propagation in DP steels is a crucial issue in fracture analysis. Accurate numerical prediction of ductile fracture initiation requires fracture models that reflect the physical mechanisms of the fracture process as reasonable as possible, yet do not require extensive material testing for calibration.

There is a wild range of ductile fracture models [3] that have been proposed based on different mechanical backgrounds, from the microscopic level in terms of voids nucleation to macroscopic point of view with continuum mechanics [4-10]. Among them, a hybrid damage mechanics model, modified Bai-Wierzbicki (MBW) has been proposed by Lian et al. [11]. It is based on the original uncoupled Bai-Wierzbicki (BW) [4] fracture model, which emphasizes the Lode angle effect on plastic deformation and ductile fracture. Its unique feature is that it differentiates damage from fracture, with an explicit damage initiation criterion and a continuum damage mechanics (CDM) based damage evolution for progressive damage accumulation until the final fracture. Due to the hybrid characteristics of the MBW model, it has the potential and flexibility in describing the ductile failure of a variety of materials featured with distinguished damage mechanisms, either with a pronounced damage evolution stage before the final rupture [11,12] or in other cases where the failure is triggered shortly after damage initiation with rapid damage evolution [13,14].

The above-mentioned models have been only developed and validated for isotropic materials. However, most of the metallic materials show anisotropic deformation behavior due to the nature of the structure as well as the processing history. Various anisotropic plasticity models in conjunction with advanced testing methods have been developed in the past decades especially for metallic material [15-19]. To improve the accuracy of the prediction on plasticity and ductile fracture, an evolving non-associated Hill48 (enHill48) model [20], describing the anisotropic hardening and Lankford coefficient (r-value) evolution at different strain levels simultaneously, has been developed. The accuracy and flexibility of the enHill48 model have been approved by the accurate cold formability prediction of the ferritic stainless steel in [21]. The extension of the enHill48 anisotropic model to predict fracture by combing the MBW fracture model has been introduced and validated in the previous study [22].

In this study, the fracture model based on the enHill48 anisotropic plasticity model is applied to a DP steel, DP1000, for describing the deformation and fracture behavior under various stress states. The steel shows only minor initial plastic anisotropy and has been described by the isotropic MBW model with satisfactory accuracy in the previous study [14]. By the current work, we aim to demonstrate that non-negligible plastic anisotropy will develop during the deformation for the material with minor initial anisotropy, and through a comparison with the isotropic MBW model, a higher level of accuracy in the description of both deformation and fracture could be achieved with the evolving anisotropic plasticity and fracture model.

2 Material and experimental characterization

2.1 Plasticity characterization

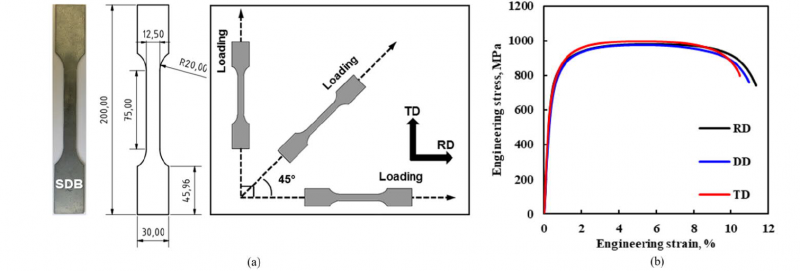
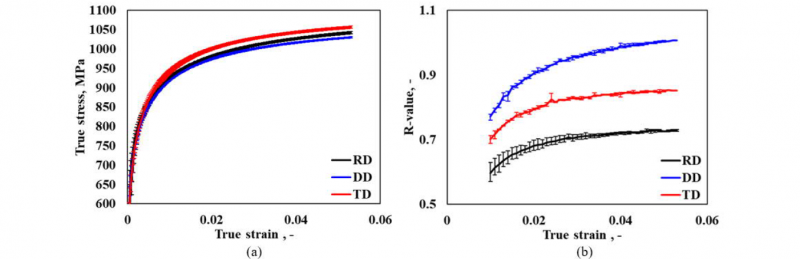
DP1000 sheet steel with a thickness of 1.5 mm has been investigated in this study. The material is composed of ferrite and martensite phases, with an approximate martensite phase fraction of 45%. The detailed microstructural characterization can be found in [23]. To characterize the material anisotropic plasticity behavior, uniaxial tensile tests of the smooth dog-bone (SDB) specimens along three different directions with respect to the rolling direction (RD) from thin sheets have been performed at room temperature (RT, 25°C) and quasi-static (QS, 0.0001 s⁻¹). The specimens have been manufactured according to DIN EN ISO 68921 [24]. The geometry design and the loading directions are shown in Fig. 1 (a). Detailed experimental setup and procedures on tensile tests can be found in our previous study [14]. The experimental engineering stress vs. strain curves along RD, transverse direction (TD), and diagonal direction (DD) from uniaxial tensile tests are shown in Fig. 1 (b). The experimental result shows that the material plasticity properties, from yield strength, ultimate tensile strength, to fracture elongation are somewhat scattered among directions. Furthermore, with an in-depth investigation on the anisotropy evolution, not only the flow stress, i.e. the hardening behavior, but also the plastic strain ratio, i.e. r-value, are evolving during the plastic deformation. The characteristic stress–strain curves and r-value evolution curves with scattered deviation among three parallel tests are shown in Fig. 2 (a) and (b), respectively. In addition, hydraulic bulge tests as described in [12], have been performed for the equibiaxial tension condition.

Fig. 1. Uniaxial tensile test specimens and results.

(a) Geometry details and loading direction sketches of the SDB specimen, (b) engineering stress-strain curves along three loading directions.

Fig. 2. The flow stress and r-value development from uniaxial tensile tests.

(a) True stress–strain curves along three loading directions, (b) r-value evolution curves along three loading directions.

2.2 Fracture characterization

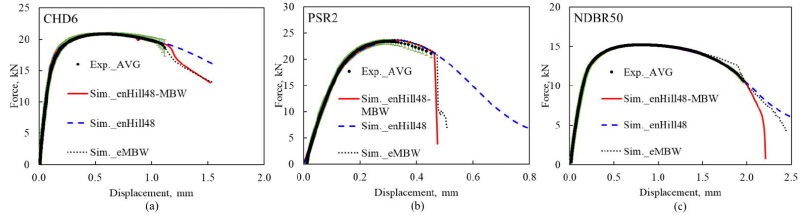
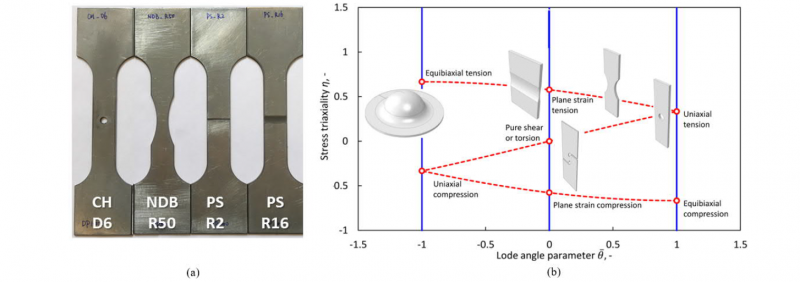
To experimentally characterize the ductile fracture properties of the investigated material, tensile tests on various specimen geometries under the QS loading conditions have been performed. A category of all flat samples at laboratory level in the current study is shown in Fig. 3 (a), including one central-hole (CH) with a diameter of 6 mm (CHD6), one notched dog-bone (NDB) specimen with radii of 50 mm (NDBR50), and two plane-strain (PS) specimens with notch radii of 2 mm (PSR2) and 16 mm (PSR16). The detailed geometry design is explained in [25]. A sketch demonstrating the characteristic stress states in the space of stress triaxiality and Lode angle parameter is depicted in Fig. 3 (b) as a reference. The characteristic force–displacement curves with scattered deviations among parallel tests according to CHD6, PSR2, and NDBR50 specimens, are shown in Fig. 4 (a), (b) and (c), respectively. PS stress states have the shortest uniform and fracture elongation, and a lower notch radius enhances the strength and brings the damage and fracture occurrence earlier. CH and NDB specimens, at the intermediate stress states, experience mediate range work hardening and elongation. From the experimental results, it can be seen that the stress state plays a dominant role in ductility.

Fig. 3. Plasticity and fracture tests over various stress states.

(a) Overview of the sample geometry, (b) experimental tests for characteristic stress states in the space of stress triaxiality and Lode angle parameter [11].

Fig. 4. Force-displacement curves from the fracture tests over various stress states.

(a) CHD6, (b) PSR2, (c) NDBR50.

3 Material models

3.1 Evolving anisotropic plasticity model

The yield criterion 𝑓 and flow potential 𝑔 of the enHill48 model are defined by Eq. (1) and Eq. (2), where the quadratic Hill48 equivalent stresses 𝜎_σ(𝝈), 𝜎_r(𝝈) are calculated based on the anisotropic parameters (𝐹_σ, 𝐺_σ, 𝐻_σ, 𝑁_σ, 𝑀_σ, 𝐿_σ and 𝐹_r, 𝐺_r, 𝐻_r, 𝑁_r, 𝑀_r, 𝐿_r) from yield stresses and r-values, respectively as Eq. (3). The flow curve along the reference direction, i.e. RD, is expressed by 𝜎_Y(𝜀̅^P). The flow potential 𝑔 controls the evolving strain components according to the non-associated flow rule (NAFR) with the equivalent plastic strain rate 𝜀̅̇^P, which is not equal to the conventional non-negative plastic multiplier 𝜆̇, as summarized in Eq. (4) and Eq. (5). Detailed derivation can be found in Lian et al. [20]. The equivalent stress 𝜎(𝝈) is adopted with the corresponding parameters listed in Eq. (6), where 𝜎_𝜃 and 𝑟_𝜃 are the flow stress and r-value along the corresponding loading direction 𝜃, and 𝜎_𝑏 is the flow stress under the equibiaxial tension condition obtained from the hydraulic bulge test. Since the material is a flat rolling sheet, only in-plane anisotropy is considered. Therefore, the parameters of 𝐿 and 𝑀 are typically set as 3 according to Aretz [26].

3.2 Hybrid damage mechanics model

In the case of proportional loading, the damage initiation locus (DIL) is formulated as a critical plastic strain 𝜀̅_ddi with the dependence of stress states as shown in Eq. (7), where 𝐷₁, 𝐷₂, 𝐷₃, 𝐷₄ are four damage initiation parameters in the symmetric DIL. To characterize the stress states, the stress triaxiality 𝜂 and Lode angle parameter 𝜃̅ are two independent variables that have been widely applied. As shown in Eq. (8) and Eq. (9), since the stress state is evolving during plastic deformation, the average stress triaxiality 𝜂_avg and the average Lode angle parameter 𝜃̅_avg have been adopted. For proportional loading, once the DIL is reached during plastic deformation, the damage initiation is triggered. The damage initiation indicator 𝐼_dd in Eq. (10), which is integrated during the accumulation of plastic strain, is applied in the non-proportional loading conditions. The ductile damage evolution is based on the energy dissipation theory and simplified as linear law. The damage evolution rate as shown in Eq. (11), is controlled by the equivalent stress at the damage initiation point 𝜎_ddi and the dissipated energy 𝐺_f between damage initiation and fracture. The critical damage value 𝐷_cr determines the ductile fracture locus (DFL) as Eq. (12). The crack propagation in finite element (FE) simulation is accomplished via element deletion, and it starts at the point when the ductile fracture indicator 𝐼_df in Eq. (13), reaches unity. The hybrid damage mechanics model, in conjunction with the enHill48 plasticity model, is implemented as a VUMAT user subroutine in ABAQUS/Explicit. To ensure the convergence and enhance computational efficiency, the tangent cutting plane algorithm has been applied [27].

4 Numerical simulations

4.1 Plasticity behavior

From the test results, the localized necking happens at a relatively small strain. Therefore, an appropriate extrapolation based on the experimental data is applied to obtain the strain hardening behavior of the material at large deformation. The flow curves of plastic deformation are derived in the formulation of the hardening function according to the combined Swift and Voce law in Eq. (14), with hardening parameters (𝐴, 𝜀̅₀, 𝑛, 𝑘₀, 𝑄, 𝛽, 𝛼). The calibration procedure is similar to the one shown in [28] with an additional modification by introducing a piecewise combination at discrete strain levels. The evolving anisotropic parameters (𝐹_σ, 𝐺_σ, 𝐻_σ, 𝑁_σ) as shown in Eq. (6), are calibrated using the flow stress obtained from uniaxial tensile tests along three distinguished loading directions as well as the equibiaxial tension condition.

The evolution of r-values, obtained from uniaxial tensile tests, is fitted by the Voce exponential law with constant 𝐶₁~ 𝐶₃ as shown in Eq. (15). Based on the r-value evolution, the evolving anisotropic parameters (𝐹_r, 𝐺_r, 𝐻_r, 𝑁_r) can be calibrated as discussed in Eq. (6).

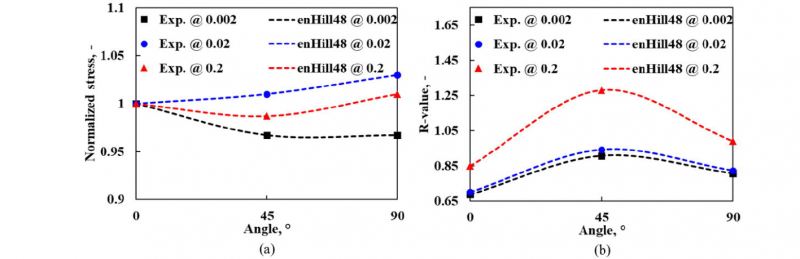
The normalized stress distribution and r-value evolution at three true strain levels 0.002, 0.02, and 0.2, i.e. from the onset of yielding until the extrapolation at large strain level along three loading directions, are depicted in Fig. 5 (a) and (b), respectively. It is evident that the enHill48 model can well capture the anisotropic plasticity of the investigated materials with high accuracy in terms of both stress and r-value distribution, especially under the consideration of anisotropy evolution.

Fig. 5. The evolution of anisotropy in experiments and calibrated enHill48 model.

(a) Distribution of normalized stress at different strain levels, (b) r-value directionality at different strain levels.

4.2 Ductile fracture

After the plasticity parameters in the enHill48 model have been calibrated and validated based on the SDB uniaxial tension and hydraulic bulge tests, numerical simulations have been conducted for other specimens to investigate the ductile fracture behavior. Half-thickness FE models have been used for all the specimens, in consideration of both the in-plane anisotropy and computational efficiency. A symmetric DIL with respect to the Lode angle parameter is assumed. From the simulation results, the global force–displacement response, as well as the local variables from the critical elements, are extracted for the construction of DIL. Based on the metallographic examination of the fracture surfaces in our previous study [25], damage initiation in DP1000 steel is found to take place at a very late stage of plastic deformation. Therefore, the critical instant, at which a sudden load drop occurs on the force– displacement curve, is determined as the damage initiation point for all specimens. The local variables 𝜀̅_ddi, 𝜂_avg, 𝜃̅_avg at the critical position and instant in these four specimens are used to calibrate the four damage initiation parameters 𝐷₁~ 𝐷₄ according to Eq.(7).

Fig. 6. Experimental and numerical simulation comparison on force-displacement responses of fracture tensile tests, with the green shaded area as the scatter among parallel tests.

(a) CHD6, (b) PSR2, (c) NDBR50.

The predicted force–displacement responses for CHD6, PSR2, and NDBR50 specimens, with enHill48 plasticity model (blue dashed lines) and enHill48 based anisotropic MBW hybrid ductile model (red solid lines), are depicted in Fig. 6 (a), (b), and (c), respectively. In addition, the previous results with the isotropic extended MBW (eMBW) model [14] indicated by black dotted lines, are also shown as a reference. From the comparison, it is obvious that the evolving plasticity model gives precise predictions on the plastic deformation behavior. The most remarkable improvement is in describing the softening behavior of the NDBR50, for which the isotropic model overestimates the force considerably. The overestimation in terms of the force also limits the fracture prediction of the isotropic eMBW model, while the enHill48 based anisotropic MBW shows a great match on force and the final fracture point. More tests with a larger range of stress states will be incorporated into the study to further exam the predictive capability of the developed model. Furthermore, a validation test focusing on the edge crack will be also developed in an upcoming study.

5 Conclusions

In this study, the plasticity and ductile fracture behavior of DP1000 steel has been investigated with a hybrid experimental and numerical method. The following conclusions can be drawn:

• From the experimental characterization, DP1000 steel is recognized with only minor plastic anisotropy at the initial deformation stage, but since the anisotropic hardening and r-value keep developing along deformation, the accumulated influence of anisotropy is noticeable and crucial to an accurate numerical prediction of ductile fracture.

• By considering the anisotropic hardening and plastic strain ratio evolution at different strain levels simultaneously, the enHill48 plasticity model gives a precise prediction on the anisotropic plastic behavior.

• The extended enHill48 model in conjunction with the MBW damage model improves the already satisfactory prediction of deformation and fracture under various stress states by the damage model based on isotropic plasticity to a great level of accuracy. It shows that even for materials with minor or moderate plastic anisotropy, considering anisotropy is critical to precisely describe the large deformation and ductile fracture behavior.

Acknowledgments

This contribution shows the current research work of the research project 'Digital solution for microstructure and process design of DP and Q&P steels with tailored mechanical property profiles'. The financial support by the Technology Industries of Finland Centennial Foundation is gratefully acknowledged. The authors wish to acknowledge the CSC – IT Center for Science, Finland, for computational resources under project 2001353.