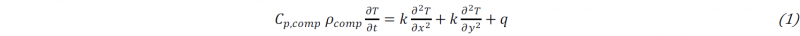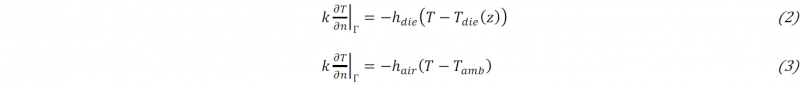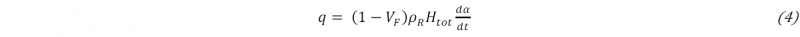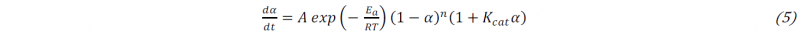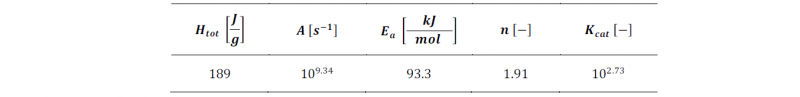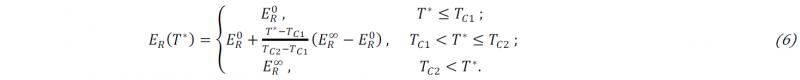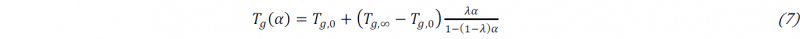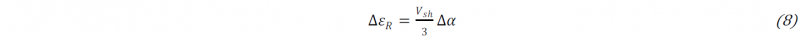1 Introduction

The last decades have been marked by the significant growth of composites application within the engineering community due to their superior properties over traditional construction materials (timber, concrete, steel) [1–4]. Fiber reinforced polymers (FRPs) exhibit such advantages as high strength-to-weight ratio, improved durability, resistance to corrosion and influence of harsh environment, ease of transportation and handling [5,6]. Among all the available techniques, the pultrusion manufacturing process is the most cost-efficient one [7]. It allows the production of straight [8,9] or curved [10,11] profiles with constant cross-section and virtually unlimited length. Pultrusion production starts from pulling reinforcement material (carbon, basalt, glass) placed on the fiber creel through a bath filled with a polymer resin (vinyl ester, polyester, epoxy) [12,13]. Subsequently, impregnated material is guided to the performer where it acquires the desired shape, and excess of resin is removed [14]. Next, the saturated pack is pulled to the heating die, where the polymerization process of resin is initialized, and curing of composite takes place [15,16]. The puller units' system then drags the cured composite out of the die and directs it to the floating saw for the final cutting of the profiles [17].

Pultrusion process involves many technological parameters affecting the quality of the final product [18,19]. The occurrence of geometrical distortions (spring-in, warpage) [20] and internal defects (cracks, delaminations) [21] are the drawbacks of any composite’s manufacturing process. However, they arise not only due to technological peculiarities, but also due to the mechanical and chemical properties of constituent materials [22]. For instance, the severity of shape distortions is significantly affected, first, by the difference in the coefficients of thermal expansion of the polymer resin and reinforcement material, and, second, by the chemical shrinkage of matrix [23]. Manufacturing-induced shape distortions lead to decreased mechanical properties of pultruded profiles at all lifecycle stages (production, storage, assembling and service). However, the pultrusion manufacturer is intended to optimize the production process by fabricating the maximum volume of profiles with the minimum geometrical and internal defects. Instead of conducting expensive trial-error manufacturing cycles and adjusting process parameters for the optimization of the pultrusion process outcome, the numerical modelling tool can be applied [24,25].

Numerical modelling of spring-in formation has already been studied in Resin Transfer Moulding (RTM) [26], Vacuum Assisted Resin Transfer Moulding (VARTM) [27], and Autoclave [28] composite manufacturing processes. To the best of authors knowledge, just a single article is devoted to the mathematical simulation of spring-in distortion in pultrusion [29]. However, in the mentioned study, the experimental verification of the proposed model is performed only at one pulling speed. The current article aims to experimentally and numerically investigate the relationship between spring-in values of pultruded L-shaped profiles and different pulling speeds of the manufacturing process. Pultrusion experiment of glass fiber/vinyl ester resin 75 × 75 × 6 mm Lshaped profiles was performed at two different pulling speeds of 200 and 600 mm/min. Spring-in angles were determined for each profile a few hours after the production process when the material acquired room temperature. Abaqus software was used for the Finite Element Analysis (FEA) of a 2D mathematical model involving both thermo-chemical and mechanical analysis of the pultrusion process. Cure Hardening Instantaneous Linear Elastic (CHILE) model was used to characterize the polymer matrix instantaneous Young’s modulus. Self-Consistent Field Micromechanics (SCFM) method was utilized to describe the unidirectional (UD) reinforcement and fabric material mechanical behavior. Numerical and experimental values of spring-in were compared.

2 Materials and Methods

2.1 Pultrusion experiment

L-shaped E-glass reinforced vinyl ester profiles were produced using Px500-6T (Pultrex, UK) pultrusion system at the Laboratory of Composite Materials and Structures of the Center for Design, Manufacturing and Materials (Skolkovo Institute of Science and Technology, Moscow, Russia). Pultrusion line was equipped with a 600 mm long die. The L-shaped profile, having dimensions of 75 x 75 mm and thickness of 6 mm, is schematically illustrated in Fig. 1a. The core zone of pultruded composites was reinforced by 104 longitudinally oriented unidirectional rovings PS 2100 (Owens Corning Composite Materials, USA; tex. 9600) with a linear density of 9600 TEX (9600 g/1000 m), while the surfaces of profiles were reinforced by two layers of E-glass fabric LT 0600/S 300/06H 01/125 GUS (Owens Corning Composite Materials, USA) having a surface density of 900 g/m². Therefore, the cross-section of the pultruded profile has a multi-layer structure. The fiber volume fraction is not homogeneous, and each layer is characterized by a different concentration of fibrous reinforcement: the overall volume fraction of reinforcement is equal to 59% in the unidirectional layer and 50% in the fabric layer. The fibrous fabrics and rovings converging to the curingforming die inlet are presented in Fig. 1b., while the cured profile leaving the die is shown in Fig. 1c.

Fig. 1. Pultrusion experimental setup: (a) Scheme of the cross-section, (b) fibrous reinforcement converging in the die inlet, (c) cured profile leaving the die.

The employed polymeric system is the combination of the vinyl ester resin Atlac 430 (DSM Composite Resins AG, Switzerland), several catalysts (BYK A555, Trigonox C, Perkadox 16), and powder of zinc stearate as an additive. The description of the kinetic behavior of the employed resin system and its composition are described in detail in a previous work [21].

The curing-forming die was heated using electrical platens clamped on the die surface, as shown in Fig. 1c. The power of the heating platens was tuned by a control system to keep the temperature on the thermocouples embedded in the steel die in the range of 145°C ± 10°C. The pulling speeds used in the performed experiment are 200 and 600 mm/min.

The shape distortions were evaluated after the profiles cooled down to room temperature. In particular, the spring-in was evaluated comparing the L-shaped profiles to a steel tool having a calibrated internal angle of 90°, according to an approach already described in several previous works [21,30].

2.2 Numerical implementation

To analyze the evolution of the shape distortions and to detect how the curing cycle affects the profiles’ deformation, the thermochemical and mechanical behavior of performed experiments were numerically modeled in ABAQUS software.

As a stationary pulling process is considered, the 2D heat conductivity equation in the material frame of reference can be expressed as following (neglecting the heat conduction in the pultrusion direction) [22,31]:

Where 𝐶_p,comp and 𝜌_comp are the specific heat and the density of the lumped composite material; 𝑇 represents the temperature; 𝑥 and 𝑦 represent the coordinates of the cross-section; 𝑘 is the thermal conductivity of the lumped composite material in the crosssectional plane; 𝑡 represents the time; 𝑞 is the exothermal heat generation of the resin related to the cure reaction. The specific heat, density, and thermal conductivity terms were evaluated, combining the properties of reinforcement and resin matrix, accounting for their fractions [31,32]. The above written Eq.1 is implemented separately for the layer with unidirectional and fabric reinforcement since different volume fraction of reinforcement is involved. Besides, the pulling speed 𝑢 is absent in Eq. 1 since it was written for the Lagrangian frame of reference. However, the term of pulling speed appears at the boundary condition equations defining interaction between the moving composite and surrounding media (die or air, respectively):

Where Г corresponds to the surface of the profile; ℎ_die and ℎ_air are the convective heat transfer coefficients between the profile and die (within the die block) and surrounding air (after profile left the die block), respectively; 𝑇_die and 𝑇_amb are the temperatures of the die block (as a function of 𝑧 coordinate) and ambient air.

The heat generation term involves the volume fraction of fiber 𝑉_F, the resin density 𝜌_R, and the total heat energy 𝐻_tot produced by the resin per unit of mass in a complete polymerization, as described by Eq. 4:

The term 𝑑𝛼⁄𝑑𝑡 is the cure rate. The kinetic of the adopted resin system follows the behavior described by Eq. 5 [21]. The kinetic parameters are reported in Table 1.

Where 𝐴 is a preexponential factor; 𝐸_α is an activation energy; 𝑅 represents the universal gas constant; 𝑛 is the order of reaction; 𝐾_cat is an activation constant.

Table 1. Resin kinetic parameters.

The mechanical model of the composite accounts for the properties of the different components involved and for their chemical evolution during the pultrusion process. While the properties of the E-glass fiber are constant during the process, the stiffness of the resin significantly changes due to the cure reaction. The variation of Young’s modulus of the resin was described by CHILE model [33]:

Where 𝑇^∗ = 𝑇_g(𝛼) − 𝑇; 𝐸⁰_R and 𝐸^∞_R represent the elastic modulus of the uncured resin (𝛼 = 0) and of the fully cured resin (𝛼 = 1), while 𝑇_c1 and 𝑇_c2 are the critical temperature respectively at the activation and at the completion of the glass transition, evaluated by dynamo-mechanical analysis (DMA) of the resin system [34,35]. The instantaneous glass transition temperature 𝑇_g(𝛼) is evaluated using Di Benedetto equation [36]:

Where 𝑇_g,0 and 𝑇_g,∞ represent the glass transition temperatures of uncured and fully cured resin, and 𝜆 is a material parameter.

The isotropic incremental resin shrinkage strain ∆𝜀_R is expressed as a function of the increment of cure ∆𝛼 and of the total volumetric resin shrinkage 𝑉_sh , as described by Eq. 8 [26]:

The mechanical behavior of the profile core (reinforced by unidirectional rovings) and outer layer (containing E-glass fabrics) is calculated using the SCFM approach [33,37].

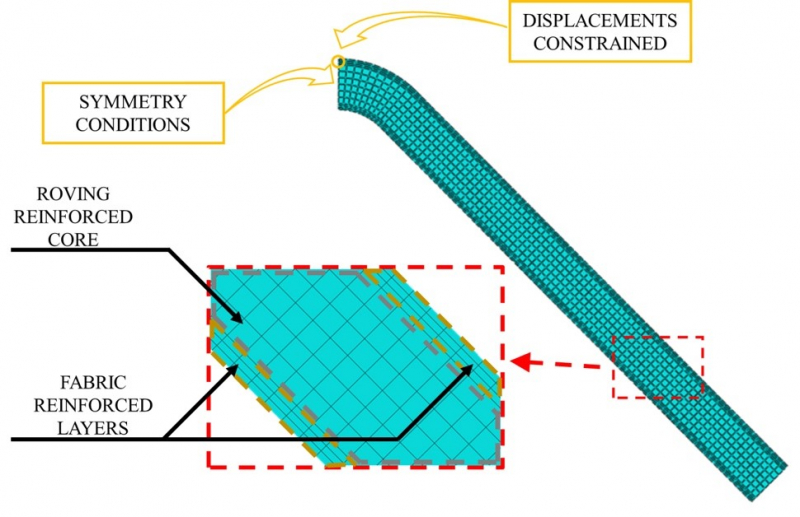
Fig. 2. Modelling of the profile cross-section and applied boundary conditions.

Fig. 2 shows the modelled and discretized 2D geometry developed in the ABAQUS software. The profile cross-section is divided into 3 zones, characterized by different mesh sizes, corresponding to the two surface layers reinforced by fibrous fabrics and the core reinforced by rovings. The surface layers have been designed 0.7 mm thick, in agreement with previous measurements performed with an optical microscope. The profile core is 4.6 mm thick. Aiming to reduce the computational effort, just half of the L-shaped cross-section geometry has been modeled applying symmetry conditions on the symmetry edge, as indicated in Fig. 2. The section has been discretized using 4-node plane strain thermally coupled quadrilateral elements (CPE4RT). The die has been modelled as a discrete rigid body. A normal hard contact condition has been implemented to describe the mechanical interaction between the die and the composite. The die displacements and the rotations of the die have been inhibited utilizing constraints applied on the L-shape tip point, as indicated in Fig. 2. Simulation has been divided in three steps, namely the initial step, the diecrossing step, and the constraint-free step.

The initial step provides the initial conditions for the simulation, which consists of null cure degree and material temperature equal to the lab temperature equal (18°C). The hard contact between the die and the profile cross-section is introduced.

In the die-crossing step the heat transfer starts. The profile of temperature evaluated by the thermocouples embedded in the steel die during the pultrusion experiment is included as an imposed temperature on the die surface. Since the thermal acquisition has been made in seven points (die entrance, five embedded thermocouples, and die outlet), the die length has been divided into six portions, and the imposed temperature in each timestep has been defined by linear interpolation of the two closest measurement points.

In the constraint-free step, the interaction between the rigid die and the FRP profile is released. In this step, the heat transfer is based on the free convection between the air at laboratory temperature (18°C) and the pultruded profile's peripheral zone.

3 Results and Discussion

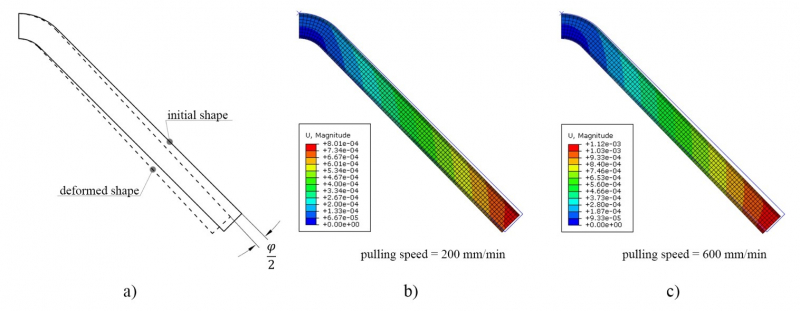
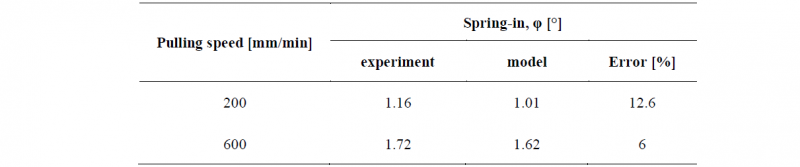
Fig. 3 shows the schematic representation of spring-in deformation (Fig. 3a) and magnitudes of displacements within the pultruded material for the profiles produced at pulling speed of 200 mm/min (Fig. 3b) and 600 mm/min (Fig. 3c). Due to the symmetry of the L-shaped profile, only its half was considered. Therefore, analyzing the numerical simulations results, half of the spring-in angle (𝜑⁄2) was calculated. Higher pulling speed provoked a higher value of spring-in distortion. Comparison of the experimental and numerical results of spring-in distortion (𝜑) are presented in Table 2. The error was 12.6% for the pulling speed of 200 mm/min, and 6% for the pulling speed of 600 mm/min.

Fig. 3. Spring-in deformation of L-shaped pultruded profile: (a) Schematic representation of spring-in deformation, (b) spring-in of profile produced at pulling speed of 200 mm/min, (c) spring-in of profile produced at pulling speed of 600 mm/min.

Table 2. Values of spring-in deformation.

4 Conclusions

An experimental and numerical investigation on pultruded glass fiber/vinyl ester resin L-shaped profiles were carried out to analyze the relationships between the pulling speed and spring-in deformation. Profiles were manufactured at pulling speeds of 200 and 600 mm/min. Values of their spring-in distortions were measured as soon as profiles cooled down to room temperature. Subsequently, the numerical model of the pultrusion process was developed in ABAQUS software. To describe Young’s modulus of resin during the polymerization reaction, CHILE approach was utilized. Mechanical properties of unidirectional and fabric layers were calculated in accordance with the SCFM theory.

Results of the pultrusion experiment and mathematical simulations were compared and found to be in a good correlation between each other. Higher pulling speed provoked more pronounced spring-in distortions. The difference between experimental and numerical results was as much as 12.6% and 6% for the pulling speed of 200 and 600 mm/min, respectively. Therefore, the developed numerical model, based on CHILE approach, is able to predict the value of spring-in deformation of L-shaped pultruded profiles with a high level of accuracy.